Особенности математической модели управления комплексом зданий с распределёнными энергосистемами

Опыт внедрения автоматизированных систем диспетчерского управления распределенными энергосистемами комплекса зданий на базе автоматизированных ИТП, представленный, например в [4], также показал высокую эффективность работы энергохозяйства на примере Белгородского государственного технологического университета им. В.Г. Шухова. Экспериментальные исследования [5] показали, что в системах, как централизованного, так и децентрализованного теплоснабжения наблюдается эффект, характерный для комплекса зданий с совместным применением автоматизированных ИТП и элеваторных узлов (при централизованном теплоснабжении, например, при подключении к внешним теплосетям через общую тепловую камеру), приводящий к снижению эффективности их функционирования и снижению экономии тепловой энергии. Особенности математической модели управления процессом отопления в автоматизированном ИТП здания и для комплекса нескольких зданий с возможностью исследования этих процессов представлены в [6, 7].

Постановка задачи. Исследуются возможности управления процессом теплопотреб-ления комплекса из 5 зданий с совместным применением автоматизированных ИТП и элеваторных узлов (в условиях ограниченных инвестиций). За основу моделирования этих объектов принят подход [6, 7].

Особенности схем моделирования. Считаем, что здания 1, 2, 3 оборудованы автоматизированными ИТП, а остальные – нерегулируемыми элеваторными узлами. Тепловая нагрузка этих зданий представлена в табл. 1.

Таблица 1. Расчетная тепловая нагрузка зданий комплекса

Номер здания	Расчётная тепловая нагрузка, ГДж/ч
Здание 1	0,489
Здание 2	0,308
Здание 3	0,91
Здание 4	0,18
Здание 5	0,15

Типовой автоматизированный ИТП для зависимой системы отопления (СО) здания содержит технологический контроллер ТК1, моноблок циркуляционных насосов Н1 и Н2 с электроприводами М1 и М2, регулирующий клапан К1 с исполнительным механизмом ИМ1, обратный клапан КО1, регулятор перепада давления прямого действия РД1 с клапаном К2, датчик температуры наружного воздуха ДТ1, датчики температуры теплоносителя ДТ2 и ДТ3, датчики давления ДД1 и ДД2, а также узел учета тепловой энергии, например, теплосчетчик с комплектом датчиков температуры, расхода и давления [7]. Схема присоединения системы отопления зданий с автоматизированными ИТП показана на рис. 1.

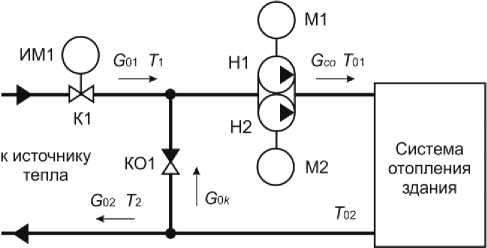
Рис. 1. Схема зависимого присоединения СО здания к тепловым сетям

Обозначения технологических величин на схеме следующие: Т 1 и Т 2 – соответственно температуры теплоносителя в подающем и обратном трубопроводах на вводе в ИТП; Т 01 и Т 02 – соответственно температуры теплоносителя в подающем и обратном трубопроводах внутреннего контура СО здания; G 01 и G 02 – соответственно расходы теплоносителя на вводе ИТП в подающем и обратном трубопроводах СО здания; G 0 k – расход теплоносителя через перемычку с обратным клапаном; G со – расход теплоносителя во внутреннем контуре системы отопления здания.

Обобщенная функциональная схема системы отопления автоматизированного ИТП здания показана на рис. 2. Состав элементов схемы следующий: блок регулятора по возмущению Р1

(погодная компенсация); двухконтурный блок регулятора Р2 по отклонению технологической величины от заданной; П1 – П3 элементы-преобразователи выходных величин датчиков температуры Д1 – Д3 (термопреобразователи сопротивления на выходе с R i ) в измеряемые ими физические величины (например, как в контроллерах типа ECL Comfort (Danfoss, Дания)); исполнительный механизм ИМ; регулирующий орган РО в виде седельного клапана; узел смешивания теплоносителей УС (см. рис. 1) от подающего трубопровода теплосетей и от обратного трубопровода СО здания через перемычку с КО1; объект управления ОУ, представляющий собой СО здания.

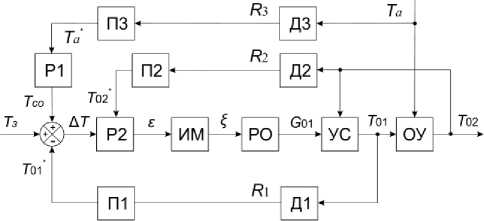
Рис. 2. Функциональная схема автоматизированного ИТП здания

Дополнительные обозначения величин функциональной схемы следующие: Т а – температура наружного воздуха; Т а ^* – температура наружного воздуха на входе в блок Р1; Т со – требуемая с учётом принципа погодной компенсации расчетная температура теплоносителя в подающем трубопроводе СО здания после перемычки с КО1 (см. рис. 1); Т з – величина задания с целью коррекции температуры теплоносителя в подающем трубопроводе СО здания ( Т со ); Δ Т – отклонение по температуре регулируемой величины T 01 ; ε – приведенный управляющий сигнал регулятора Р2; ξ – приведенная величина перемещения РО; Т 01^* – измеренная температура теплоносителя в СО здания; Т 02^* – измеренная температура теплоносителя на входе в Р2.

Системы уравнений математического моделирования . Математическая модель СО здания на основе автоматизированного ИТП [6] в соответствии с функциональной схемой и с учётом структур регуляторов Р1 и Р2 (в целях упрощения схемы на рис. 2 их структуры не раскрыты) представлена в виде системы уравнений (1).

Система (1) включает следующие уравнения: уравнения движения датчиков температуры Д3 и Д1; уравнения для регуляторов Р1 и Р2 (уравнение отопительного графика для вычисления расчетной температуры теплоносителя в подающем трубопроводе СО здания Тсо; уравнение связи для определения ΔТ; нелинейное уравнение зоны нечувствительности регулятора Р2; уравнение регулятора Р2 для управления в системах теплоснабжения, например, по аналогии со специализированными контроллерами типа ECL Comfort; нелинейное уравнение зоны ограничения Р2); уравнение исполнительного механизма (считается интегрирующим звеном); уравнение РО относительно выходной величины G01 с учётом определяемой в расчётах величины G1; уравнение связи для УС; уравнение движения ОУ по каналу регулирования «температура теплоносителя Т02 -температура теплоносителя Т01»; уравнение движения датчика температуры Д2.

*

Tda-Ta^t) + Ta'(1) = kdaTa (1 )’ dt

*

^- oi ⁽ t )   j *(A = fc T

T-1      ,      + 101 (t)   k- 1T 01(t)’ dt

T eo ( t ) = f (T a *),

A T ( t ) = T_m ( t ) + T ( t ) - T o1* ( t ),

J0’ — X- -AT(t) < X-’ x (AT) = <          .      .

’   [ k 1 A T ( t ), |A T ( t )| >  X - ,

« ( t ) =   [    T ) T u + A^ T * ,

J k ₂ £ ⁽ t )’ ^{- k} _m <  £ ⁽t ) <  k m ’

X, ( t ) = 5

[ ^k m ’ k ⁽ t )l >  ^k m ’

=       , ( t )’

^{-t     T} u

G 01 ( t ) = G 1 k_ke k ² ^ ⁽ t ) ,

T 1 G 01 (t) + T 02 (t)(G eo - G 01 (t)) = G eo T 01 (t) ’

-²T 02 ( t )              -T 02 ( t )

^T 1 ^T 2     , 2     ^{+ ( Т} 1 ^{+ T} 2 )     ,     ⁺ T 02 ⁽ t ) = ^kT 01 ⁽ t )’

-t                -t

*

T-2 -T0|-(-) + T02*(t) = k-2T02(t)’ dt

Дополнительные обозначения в системе уравнений (1) следующие: τ di и k di – соответственно постоянная времени и коэффициент передачи i -го датчика температуры; G co – расход теплоносителя во внутреннем контуре СО здания, определяемый циркуляционным насосом (см. рис. 1); G 1 – номинальный расход теплоносителя на входе РО; x 1 (Δ Т ) – выходная величина нелинейной зоны нечувствительности регулятора Р2; x 2 ( t ) – выходная величина нелинейной зоны ограничения (насыщения) в регуляторе Р2; k 1 и k 2 – коэффициенты пропорциональности соответственно нелинейных зон нечувствительности и ограничения регулятора Р2; X d – зона нечувствительности регулятора

Р2; X p – зона пропорциональности регулятора Р2; Т и – постоянная регулятора Р2.

Модель водоструйного элеваторного узла в нерегулируемых тепловых пунктах зданий представляется в виде трехходового смесительного клапана с фиксированным коэффициентом подмеса, определяемым соотношениями расходов G 01 и G co . С учетом этого система уравнений, описывающих СО здания с элеваторным узлом, имеет следующий вид:

G 01 ( t ) + G 0 k ( t ) = G eo ( t ),

■ T 1 G 01 (t) + T 02 (t)(G eo — G 01 (t)) = G eo T 01 (t) ’

TT 2 ^-^Гг^-1 + ( T 1 + t ₂) ^- T^ + T 0 ₂( t ) = kT 01 ( t ).

I        -t                   -t

Уравнение для определения величины тепловой мощности W ( t ) в каждом здании с учётом применения автоматизированных ИТП или элеваторных узлов следующее:

W (t) = G01(t)T1( t) - G02(t)T2( t). (3)

Расходы теплоносителя на вводах тепловых пунктов комплекса зданий существенно зависят от положения штоков регулирующих клапанов в автоматизированных ИТП. Определение соотношения расходов выполняется на основе экспериментальных исследований для зданий комплекса с учетом системы уравнений следующего вида:

n

Z Gj( t) = G 0’ j=1

n

m

Z Sj (t) Gj( t) Gj (t)-Z H „( t) = 0’ j=1                                     i=1

Sj (t) = APj (t)/ G 22( t)’

G pj (t)=-—G0— Z V Sj( t)/St (t) k=1

.

Здесь G 0 – общий расход теплоносителя в гидравлической системе комплекса из 5-ти зданий; G j – расход теплоносителя на вводе j – здания; S j – гидравлическое сопротивление на вводе j – здания; H нi – напор, создаваемый сетевыми насосами; Δ P j – перепад давления между подающим и обратным трубопроводами на вводе j – здания; G pj – расчётный расход теплоносителя на вводе j – здания, определяющий расход G 1 в системе уравнений (1); S k – гидравлическое сопротивление на вводе k – здания.

Математическая модель в виде систем уравнений (1), (2) и (4) [7], дополненных экспериментальными данными, позволяет определять параметры теплоносителя на входе и выходе исследуемого комплекса зданий при любых изменениях, вызванных, в том числе, изменениями температуры наружного воздуха или качественным регулированием тепла в автономных источниках тепла, количественным регулированием в автоматизированных ИТП и др.

Основные результаты расчётов. С помощью имитационного моделирования в среде Simulink исследуем возможности управления процессом теплопотребления комплекса из 5 зданий с совместным применением автоматизированных ИТП и элеваторных узлов. Используем систему уравнений (1) для зданий с автоматизированными ИТП, систему уравнений (2) для зданий с элеваторным узлом, а также систему уравнений (4) для расчёта перераспределения расходов исследуемого комплекса зданий. Для определения величины тепловой мощности в зданиях комплекса используем уравнение (3).

Параметры моделирования. В начальный момент времени t =0 выполняется переход автоматизированных ИТП здания 1 и здания 3 в режим пониженного теплопотребления за счет уменьшения величины T з на 3°C, а в автоматизированном ИТП здания 2 осуществляется переход в режим натопа (за счет увеличения T з на 3°C), причём с запаздыванием по времени на 15 мин. относительно исходных процессов в здании 1 и в здании 3. Длительность имитационного моделирования t m 0 составляет 2 часа 30 мин. Исходные параметры для моделирования и для зданий представлены в табл. 2.

Таблица 2. Исходные параметры для моделирования

Наименование параметра, его обозначение	Величина и размерность параметров
	здание 1	здание 2	здание 3	здание 4	здание 5
коэффициент преобразования, k	0,76	0,75	0,73	0,81	0,79
постоянная времени, τ 1	1369 с	1317 с	1380 с	903 с	886 с
постоянная времени, τ 2	558 с	619 с	571 с	290 с	343 с
максимальный расход в СО здания, G со	16 м3/ч	14 м3/ч	19 м3/ч	9 м3/ч	7 м3/ч
номинальный  расход  на вводе в здание, G 1	14,7 м3/ч	10,2 м3/ч	17,5 м3/ч	5,7 м3/ч	4,6 м3/ч
температура    наружного воздуха, T a	-1,0 °C
начальная температура теплоносителя T 1	66,0 °C

Основные типы датчиков температуры в системе автоматизации ИТП и их параметры представлены в табл. 3.

Таблица 3. Постоянные времени датчиков температуры

Тип датчика	Назначение	Условное обозначение	Величина, размерность
ESMU-100	погружной датчик температуры теплоносителя в гильзе	τ d 1	32 с
ESMT	датчик температуры наружного воздуха	τ da	900 с

Основные характеристики регулирующего клапана РО типа VB2 фирмы Danfoss представлены в табл. 4.

Основные характеристики исполнительного механизма AME 20 фирмы Danfoss для работы с регулирующим клапаном VB2 представлены в табл. 5.

Таблица 4. Характеристики регулирующего клапана типа VB2

Наименование параметра, его обозначение	Величина, размерность
диаметр, D у	40 мм
коэффициент, k kvs	25 м3/ч
условное давление, Р у	2,5 МПа
температура, Т min	5 °C
температура, Т max	150 °C
ход штока, h	10 мм

Таблица 5. Характеристики исполнительного механизма типа AME 20

Наименование параметра	Величина, размерность
напряжение	24 В
частота	50/60 Гц
потребляемая мощность	4 Вт
тип управляющего сигнала	Аналоговый
развиваемое усилие	450 Н
ход штока	10 мм
время перемещения штока на 1 мм	15 с/мм
входной сигнал 1	0 – 10 В; R i = 24 кОм
входной сигнал 2	0–20 мА; R i =500 кОм
выходной сигнал	0(2) – 10 В
минимальная температура окружающей среды	0 °C
максимальная температура окружающей среды	55 °C

Основные значения параметров блоков регулирования технологических контроллеров ТК1 (аналогичны специализированным контроллерам типа ECL Comfort) в автоматизированных ИТП представлены в табл. 6.

Начальные значения параметров для имитационного моделирования представлены в табл. 7.

Результаты имитационного моделирования. Результаты расчётов изменений величин тепловой мощности (измеряется в МВт) для зданий с автоматизированными ИТП и с элеваторными узлами представлены соответственно на рис. 3а и рис. 3б.

Таблица 6. Параметры контроллеров ТК1 в автоматизированных ИТП

Наименование параметра, его обозначение	Величина, размерность
	здание 1	здание 2	здание 3
зона нечувствительности X d	0 °С	0 °С	0 °С
зона пропорциональности X p	90 °С	90 °С	86 °С
коэффициент преобразования k m	100 %	100 %	100 %
постоянная Tu	13 с	10 с	12 с

Таблица 7. Начальные параметры для имитационного моделирования

Наименование параметра, обозначение	Величина и размерность параметров
	здание 1	здание 2	здание 3	здание 4	здание 5
начальная температура теплоносителя в системе, T 2	45,1 °C	44,8 °C	43,3 °C	42,7 °C	41,6 °C
начальный расход на вводе в здание, G 01	11,2 м3/ч	7,7 м3/ч	13,7 м3/ч	3,9 м3/ч	3,0 м3/ч

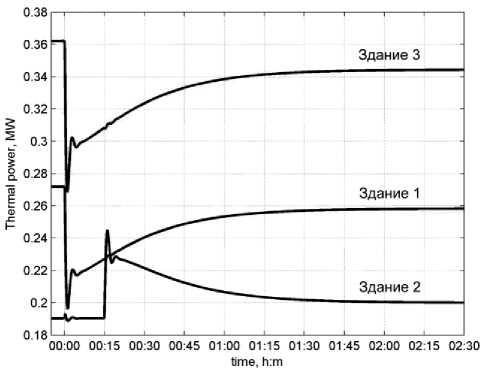
а

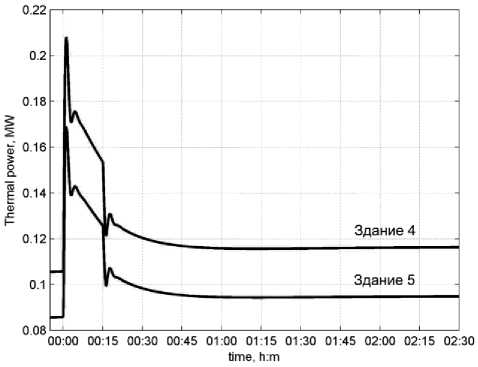
б

Рис. 3. Характеристики тепловой мощности для комплекса из 5 зданий

Характеристики процесса изменения температуры теплоносителей в обратных трубопроводах исследуемых СО зданий показаны на рис. 4.

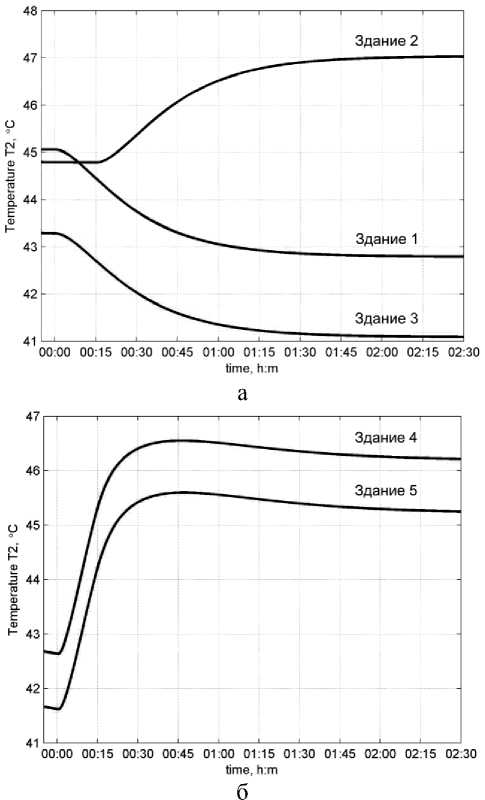
Рис. 4. Температура теплоносителей в обратных трубопроводах СО зданий с автоматизированными ИТП ( а ) и с элеваторными узлами ( б)

Из анализа характеристик на рис. 3 а следует, что исходные величины тепловой мощности при переходе автоматизированных ИТП здания 1 и здания 3 в режим пониженного теп-лопотребления (при снижении величины Тз) после окончания переходных процессов в целом уменьшаются, а в автоматизированном ИТП здания 2 за счет увеличения Тз - тепловая мощность W(t) по отношению к начальной величине возрастает. Одновременно с переходными процессами в автоматизированных ИТП протекают динамические процессы и в элеваторных узлах, причём при скачкообразном уменьшении величин W(t) в автоматизированных ИТП здания 1 и здания 3 в первые моменты времени тепловая мощность W(t) в них скачком увеличивается до некоторой величины, а затем по экспоненциальному закону уменьшается по времени до момента времени tm =15 мин. Затем при дальнейшем увеличении в автоматизированном ИТП здания 2 температуры Тз наблюдается скачкообразное уменьшение величин W(t) в элеваторных узлах с последующим их плавным переходом в установившийся режим. В исследуемом случае в элеваторных узлах в целом тепловая мощность W(t) по отношению к начальной величине возрастает.

Полученные результаты исследований подтверждают экспериментальные данные [5] и результаты имитационного моделирования [7] о наблюдаемом эффекте, характерном для комплекса зданий с совместным применением автоматизированных ИТП и элеваторных узлов, приводящий к снижению экономии тепловой энергии при переходе в режим пониженного теплопотребления автоматизированных ИТП зданий. Однако в отличие от данных [5, 7] установлено, что при переходах автоматизированных ИТП здания 1 и здания 3 в режим пониженного теплопотребления, а автоматизированного ИТП здания 2 в режим натопа, причём с запаздыванием по времени, также в этом случае для исследуемого комплекса зданий с учётом 2-х зданий с элеваторными узлами наблюдается эффект, приводящий в целом к снижениям как эффективности функционирования распределённых энергосистем этого комплекса, так и экономии тепловой энергии.

Сравнительный анализ результатов на рис. 3 и рис. 4 показывает, что при переходных процессах в тепловых пунктах комплекса зданий наблюдаются существенные колебания величин тепловой энергии, тогда как в обратных трубопроводах температуры теплоносителей Т ₃₂ полностью сглаживаются каждой системой отопления здания, т.е. СО комплекса зданий функционируют как низкочастотные фильтры.

Выводы:

• 1.    Представлены особенности математического моделирования управления процессом перехода автоматизированных ИТП двух зданий в режим пониженного теплопотребления и неодновременного перехода автоматизированного ИТП здания 2 в режим натопа с учётом влияния этих процессов на динамику зданий с элеваторными узлами.

• 2.    С помощью имитационного моделирования в среде Simulink на основе математической модели в виде систем уравнений (1), (2) и (4) исследованы особенности совместного функционирования автоматизированных ИТП и элеваторных узлов и показано, что при переходных процессах в тепловых пунктах комплекса зданий

• 3.    В условиях ограниченных инвестиций при реконструкциях существующих систем теплопотребления зданий на базе элеваторных узлов необходимо учитывать, что частичное создание автоматизированных ИТП для комплекса зданий приведёт в целом к снижению экономии тепловой энергии, если не применять при этом определённых технических решений для устранения отрицательных эффектов от оставшихся элеваторных узлов.

наблюдаются существенные колебания тепловых мощностей, тогда как в обратных трубопроводах температуры теплоносителей полностью сглаживаются каждой системой отопления здания.