Особенности моделирования гидродинамики рабочего процесса шестеренного насоса

d (rgPg) + d (rgPau) = £ dt          dxi         “.

Уравнение сохранения количества движения:

^{д (} P m^U) ₊ ^d (P m uu) ∂ t         ∂ xⁱ

∂ P

+ ∂ x

∂ ( τ ^ij) ∂ x ^j

+ ρ m r α gⁱ , (2)

где r_a , u , p_a , S_a - соответственно объёмная доля фазы α , компоненты скорости в декартовой системе координат, плотность компонента и источниковый член фазы α ; gⁱ - ускорение свободного падения; p m и p m - плотность и динамическая вязкость смеси соответственно; τ ^ij – тензор напряжений, соответствующий сдвиговым деформациям слоя жидкости, который из закона Стокса в данном случае примет вид:

ij

^T = P m

( д U ди¹ ^

+      ,

( д x дx i J ’

Тензор напряжений определяет потери на трение, возникающие вследствие вязкости жидкости.

Предполагается, что источник массы S _α возникает из межфазного переноса и таким образом удовлетворяет условию:

N

∑ S _α =0 .                (4)

α =1

Также накладывается условие, что фазы смеси заполняют весь рассматриваемый объём смеси:

N

∑rα=1.(5)

α =1

Уравнение полной энергии системы:

(^Pp tot ^)l- .^ P + V (p - U - h.,) =

∂t     ∂t(6)

= V(X V T )+V (U. t) + U. Sm + Se , где htot – полная энтальпия:

htot=h+21U2,(7)

где h = f ( T , p ) – статическая энтальпия; λ – теплопроводность; Т – температура; S_E – поток энергии.

Компонент V (U - t) в уравнении (6) выражает работу под действием внешних сил – работу сил вязкости, и отражает внутренний нагрев из-за наличия вязкости. Компонент U ⋅ S_M выражает работу под действие внешнего источника количества движения.

Начальное условие задается выражением: при t ≤ 0, V = 0 , где V – скорость потока.

Граничные условия:

• -    на неподвижных стенках элементов конструкции – V = 0 ;

• -    на подвижных стенках шестерен - V = V_m , где У_ш - скорость вращения на периферийных диаметрах шестерен;

• -    на входной границе насоса - Р = Рвх ;

• -    на выходной границе насоса - Р = Рвых .

Граничные условия для температуры:

• -    на входе в насос, Т=Твх ;

• -    на выходе из насоса, Т=Твых ;

• -    на поверхностях шестерен изменение температуры равно нулю.

Поток жидкости является турбулентным. Поэтому, движение жидкости и параметры переноса описываются не только тремя уравнениями сохранения, но еще и двумя дополнительными уравнениями для кинетической энергии турбулентных пульсаций и для описания диссипации кинетической энергии.

При этом производилось сравнение различных моделей турбулентности: k - ε , k - ω и модели Ментера Shear Stress Transport (SST) [6]. Исходя из результатов этого сравнения, в качестве основной была выбрана SST модель, использующая автоматическую функцию стенки. Данная модель базируется на двух уравнениях: уравнениях для кинетической энергии турбулентности k и её частоты ω . При этом в пристеночной области течения используется k - ω модель турбулентности, во внешнем потоке используется k - ε модель. Здесь ε – это диссипация кинетической энергии. Уравнение для определения кинетической энергии турбулентности и её частоты имеют вид:

dk

—=V-((v+^УтЖ)+Pk-e*«k; (8) dt d^ = V- ((v + omvT)V®) + Y Pt dt                           vT

-

- в® ² + ( 1 - F ) ^ ^ ^^~ ( V k) - ( Va ), ω

где

k

ν _T =    – турбулентная вязкость; P _k – член,

ω отвечающий за генерацию вихрей; F1 – функция, при помощи которой происходит переключение между k -ω и k - ε моделями.

Константы, входящие в уравнения (8) и (9), приведены в табл. 1.

Моделируемый поток является нестационарным, вязким, турбулентным, и многофазным. В этом случае рабочая жидкость представляет собой смесь основной компоненты рабочей жидкости (масло) и паров воздуха, растворенных в нем.

Наиболее распространённым подходом для учёта неравновесных явлений (кавитации) является введение в уравнения переноса источниковых слагаемых, регулирующих межфазный мас-сообмен. Большинство этих моделей базируются на уравнении Релея-Плессета [7], которое описывает рост и схлопывание одиночного пузырька в ближнем поле распределения давления.

В предлагаемой модели используется модель кавитации, представленная в работе [8] также, основанная на уравнении Релея-Плессета. Уравнение Релея-Плессета описывает динамику парового пузырька в жидкости и имеет вид:

Таблица 1. Модельные коэффициенты для SST модели турбулентности

Параметр	Значение	Параметр	Значение
p .	0,09	p;	0,09
A	0,055	A 2	0,0928
a x	0,25	Y	A _ ° « к 2 A * р з*
^ k 1	0,85	^k г	1,0
^ « 1	0,5	^ю г	0,81

R B

d ² R_r 3 (dR

________B ।             B dt2    2 ( dt )

+ 2 . = P v -P R b    P m

где R_B – радиус газового пузырька. Примем начальный радиус пузырька равным R_B =10 ^-6 м; σ – коэффициент поверхностного натяжения между основной компонентой и её парами; P _V – давление внутри газового пузырька. При этом счи-

тается, что оно равно давлению насыщенного пара Р_П .

При моделировании кавитационных процессов зачастую пренебрегают выражениями второго порядка и коэффициентом поверхностного натяжения в уравнении (10). При этом оно

редуцируется до вида:

dR B = 2 P v -P dt P P m

Величина изменения массы одиночного пу-

зырька вычисляется из выражения:

dm

B dt

= 4 < Pv^

2 P v -P

3 pv

Если в единице объёма несколько пузырьков NB, объёмная доля пара будет выражаться через уравнение:

r = VN = -rR2 N      (13)

v в в з B B,             '

тогда, величина полного переноса массы между фазами вследствие кавитации, приходящаяся на единицу объёма имеет вид:

R

1 VAP

S lv

= <

³ r NUC⁽ 1 r V ) ^PV R B

12 P-P „ „ --V—, если P <  P, ³ P k

F

1 COND

3 r v P v 2 P v -P

^RB V ^{3 P}K

, если P >  P V

где F – эмпирический настроечный коэффициент, который в случае описания процессов парообразования равен F vap=47, а в случае описания процессов конденсации – F cond=0,088; r _NUC – объёмная доля центра парообразования, равная r =5-10 -⁴

^r NUC              ^.

Данная модель хорошо работает как для описания конденсации пара, так и для про-

цессов парообразования. Однако в ней есть существенное допущение, базирующееся на предположении о том, что кавитационные пузырьки не контактируют друг с другом. Данное предположение физично только на ранней стадии кавитации. С ростом объёмной доли пара, плотность центра парообразования должна соответственно падать.

Описанные выше уравнения и их назначения представлены на рис. 1. В совокупности они и образуют гидродинамическую модель шестеренного насоса.

Задача рассматривалась в трехмерной постановке, т.к. питающий и напорный трубопроводы соосны осям вращения шестерен, что приводит к дополнительной закрутке как на входе в насосе, так и на его выходе. Составленные уравнения решались с помощью коммерческого кода ANSYS CFX [9]. Последовательность решения задачи приведена на рис. 2.

Для решения задачи было построено 18 сеточных моделей, каждая последующая получалась путем поворота предыдущей модели на 1 градус. Начало системы координат при построении геометрической модели расчетной области совпадало с серединой отрезка, соединяющего центры шестерен.

Расчетная область представлена на рис. 3. Исследовалась лишь область канала, напрямую соединяющего вход и выход насоса.

Для наглядности и удобства решения использовалась оболочка AnsysWorkbench, позволяющая связывать несколько проектов в общий.

На рис. 4 представлена созданная сеточная модель, состоящая из 2 млн. ячеек. Ячейки имеют форму треугольных призм. Для разрешения пограничного слоя использовались призматические элементы, построенные вдоль твердых стенок шестерен.

Для разрешения пограничного слоя на границе твёрдого и жидкого тел, были построены пристеночные слои (в случае неструктурированных сеток для этого использовались призматическая сетка). Расчёт толщины первой ячейки проводился в следующей последовательности:

- определение числа Рейнольдса:

Течение

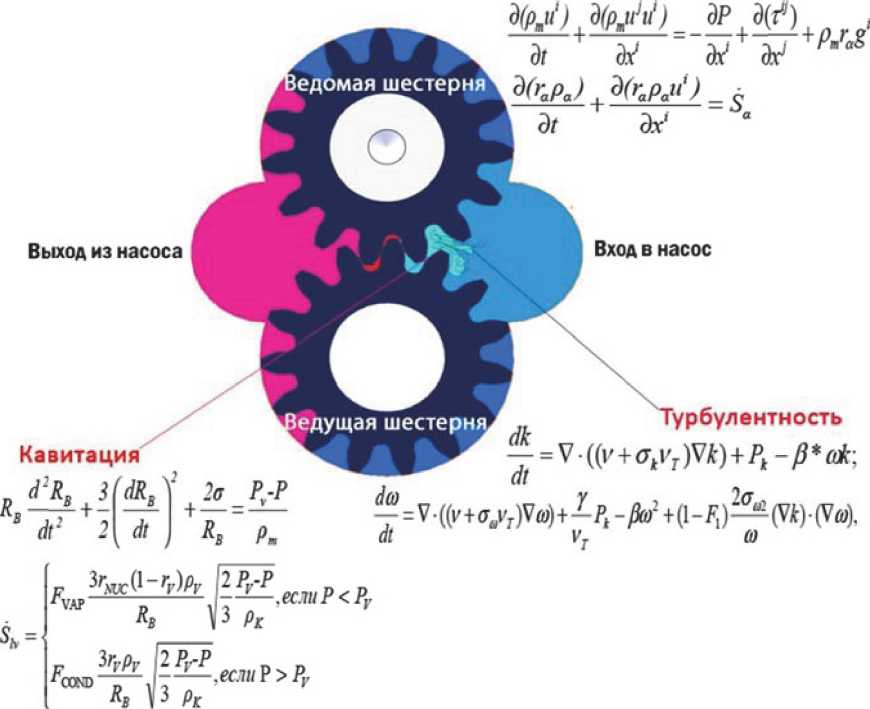
Рис. 1. Графоаналитическое представление гидродинамической модели

SolidWorks

Геометрические модели расчетных областей

Ansys Workbench

• •    Построение сеточных моделей

• •    Задание граничных условий

• •    Задание начальных условий решения

• •    Задание параметров решения

• •    Решение системы уравнений

• •    Анализ решения

Рис. 2. Процесс создания математической модели исследования запертого объема

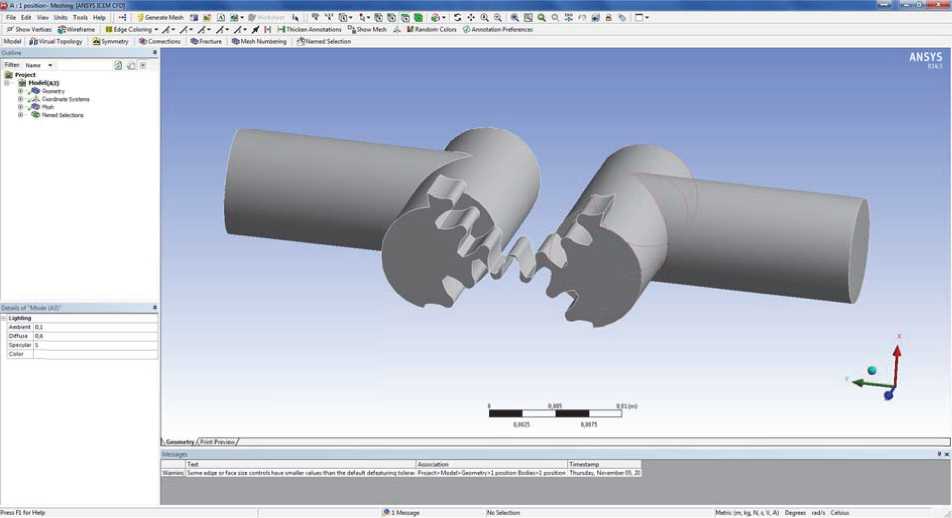
Рис. 3. Внешний вид расчетной области

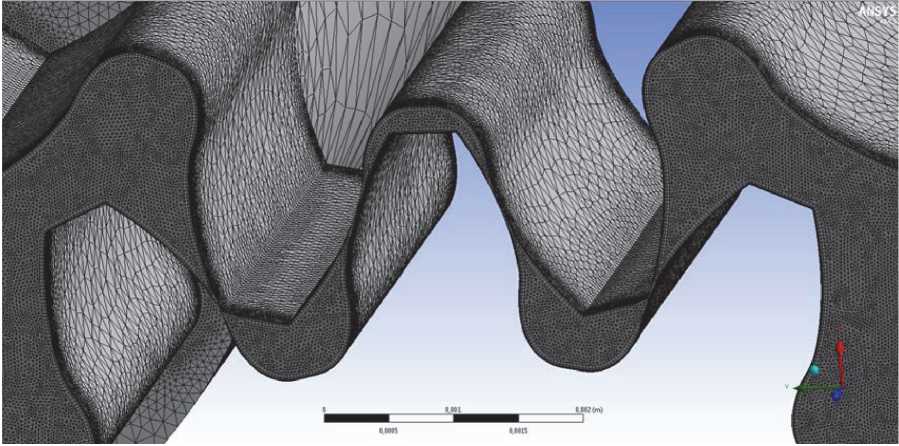
Рис. 4. Сеточная модель

Re = PUD ,

Ц

U t

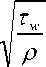
где D – характерный размер сечения в различных сечениях проточной части насоса.

• -    определение коэффициента внутреннего трения в пограничном слое:

  _ 0 , 078

  ^{С /} = 1^ ;

  
  
  
  

• -    определение касательного напряжения на стенках:

T w = -C f р • U ²;          (17)

- определение скорости, касательной к стенке:

- исходя из необходимого значения y+ из вы- ражения yp

yV. Ut ’

• -    определяется толщина первого слоя y_p .

В действительности всегда присутствует контакт между шестернями, но при проведении численного моделирования они всегда разъединены на величину наименьшего в модели элемента.

Дискретизация описанных уравнений проводилась за счет применения метода конечных объемов.

Для каждой физической величины в каждом дискретном объеме решается балансовое уравнение для каждой переменной:

• —    j pф dV + J p ( v - v g ) • ndS =

dt V         d V

• =    J t ^ V ф-p^ v - v g ) • ndS + J o_ф dV , (20) d V                             V

где 5 S i - прирост площади поверхности i во время ∆t.

Результаты расчета представлены в виде профилей скорости (рис. 5).

Разработанный метод позволяет определить колебания массового расхода на входе и выходе шестеренного насоса. Эти колебания могут быть использованы в механической и акустической моделях для расчета механи-

-luid 1 Velocity /ector 1

—r 2 722e+OOO

1 2.041 e+000

1.361e*000

6.805e-001

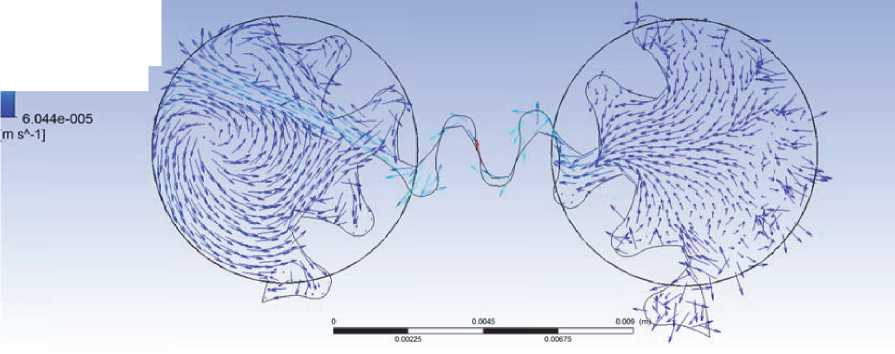
Рис. 5. Поле скоростей в среднем сечении рабочей камеры насоса

где V – объем ячейки; dV – граница ячейки; плотность жидкости; v – скорость жидкости; v _g – скорость сетки в пределах границы dV ; Т ф - коэффициент диффузии параметра; о_ф -источниковый член.

После пространственной дискретизации приведенное выше уравнение примет вид:

• —    ( p_c Ф S_c )+У рФ L ( v - v_ \г =

С Q ТС Q С Q / ^^fjl'Jl i ^g

—t v                 i =1

• =    Z ^т Фfi^li V ^ф /iⁿ + ^ Ф_с . S c 0

i =1

При этом соответствующие дифференциалы находятся из выражений:

(pc Ф sc )n+1 - Pc Фс sc ^П

( p Ф S )  У С0 ~С0 С0 ZУ С0 ~С0 С0 / dt Wc0^С0 С0?-             дt

;(22)

Отметим, что при использовании динамических сеток, описанный метод нахождения изменения параметров является единственно возможным.

При этом:

S c 01' = S C 0 + Е а $ , ;       (23)

i = 1

ческих нагрузок и излучаемого шума и тем самым решать задачи по совершенствованию конструкций насосов внешнего зацепления.