Особенности моделирования распределения энергии электронного пучка для процесса электронно-лучевой сварки

Введение. Совокупность энергетических и технологических параметров процесса определяют качество сварного шва при электронно-лучевой сварке (ЭЛС). Электронный пучок представляет собой источник высококонцентрированной энергии. Формирование глубокого проплавления фокусированным электронным пучком достигается за счет образования парогазового канала, в котором транспортируется энергия пучка. При этом сварочный шов имеет кинжальную форму с характерным грибовидным формированием в верхней части. Процесс формирования сварного шва в этом случае носит колебательный характер с периодическим неустойчивым каналом проплавления. Грибовидное расширение сварного шва в верхней части связано с периодическим рассеиванием пучка на парах металла. Такой процесс сварки редко используется на практике кроме случаев сквозного проплавления. Остроконечная форма сварного шва в корневой части приводит к образованию корневых дефектов – пустот, возникающих за счет вытеснения жидкого металла каналом проплавления. Для того чтобы такие дефекты не возникали необходимо сформировать более широкую корневую часть шва. Простейшим способом формирования радиуса в корне шва является расфокусировка электронного пучка, которая используется на практике в основном на установках с ускоряющим напряжением 30–60 кВ. Расфокусировка пучка не приводит к полному устранению корневых дефектов, кроме того шов принимает форму близкую к треугольной, уменьшается глубина проплавления, возникают деформации и напряжения, поэтому расфокусировка электронного пучка используется только при ЭЛС изделий малых толщин [1].

Для предотвращения корневых дефектов необходимо формировать пародинамический канал с достаточно широкой нижней частью. С технической стороны наиболее эффективным способом воздействия на формирование канала проплавления является осцилляция электронного пучка на поверхности свариваемого изделия. Современная тенденция развития технологии сварки заключается в применении разверток сложной формы для формирования швов с заданной формой поперечного сечения. Иллюстрация примера такой разработки, выполненной компанией Steirgerwald Strahltechnik, приведена на рис. 1. Применение цифровых генераторов сигналов позволяет создавать растры любой формы с достаточно высоким разрешением до 24 разрядов, что открывает широкие возможности в области термической обработки, сварки и пайки, а также играет ключевую роль при решении задачи наведения на стык [2].

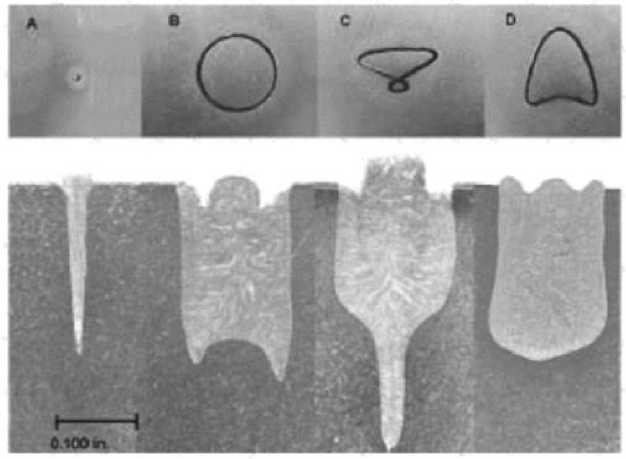
Рис. 1. Влияние траектории развертки пучка на поперечное сечение сварного шва: А – отсутствие развертки; В – окружность; С – восьмерка; D – наконечник стрелы

• Fig. 1.    Influence of the beam scanning trajectory on the weld cross-section:

A – without scanning; B – circle; C – eight; D – arrowhead

Методика выбора формы развертки электронного луча до настоящего времени не разработана. В то же время накоплено довольно большое количество экспериментальных данных [3]. Наиболее широко используются следующие развертки пучка: продольная [4], х-образная [4–6], круговая и эллиптическая [6–9], дуга и скоба [10–13]. Амплитуды разверток обычно изменяются в пределах 1–3 мм.

Электронно-лучевая сварка с вращением электронного пучка по круговой траектории позволяет добиться существенного уменьшения корневых дефектов и пикообразования, однако, ввиду того что плотность мощности в центральной части зоны нагрева мала, использование круговой развертки приводит к уменьшению глубины проплавления по сравнению с электронно-лучевой сваркой неподвижным пучком. Недостатком круговой развертки электронного пучка является также различие направлений движения пучка на противоположных кромках сварного шва. При этом на одной из кромок направление движения пучка совпадает с направлением скорости сварки, а на другом – противоположно ему, что может приводить к неравномерности формирования шва.

В работе [14] авторами была разработана новая траектория сканирования на основе ввода энергии. В исследовании предлагается, подавать на модуль управления пучком не контур, а сразу траекторию, по которой следует луч. В результате экспериментально были получены номинальная плотность энергии и функция модуляции, что позволило определить оптимальную энергию на вводе. Однако, данный метод определения энергии, предложенный авторами, энерго- и ресурснозатратный. Иллюстрация такой разработки приведена на рис. 2.

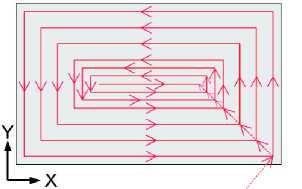
Рис. 2. Новые траектории для плавления прямоугольной области

• Fig. 2.    New paths for melting a rectangular region

В работе [15] приведены экспериментальные исследования по применению различных разверток электронного пучка с целью качественного формирования сварных соединений. Исследовалось влияние следующих разверток: круговая и эллиптическая, х-образная, зигзаг, буравчик, растр, треугольник, гребля веслами по изотермам. Исследования показали, что наилучшей разверткой по качеству формирования сварного шва является растр, в котором сканирование пучка по координате, совмещенной со стыком свариваемого изделия, осуществляется по одностороннему пилообразному закону, при этом пучок перемещается из передней части ванны в хвостовую по линейному закону с последующим мгновенным возвращением в переднюю часть. Такое сканирование способствует переносу расплавленного металла в хвостовую часть сварочной ванны. За одно сканирование вдоль стыка осуществляется 16, 32 или 64 сканирования поперек стыка по двухсторонней пилообразной траектории. Период сканирования вдоль стыка был равен 1–2 мс.

Более детальные исследования со сканированием в виде растра выявили, что при увеличении амплитуды сканирования вдоль стыка от 5 мм при сварке малых толщин до 15 мм при сварке средних толщин парогазовый канал трансформируется в устойчивую полость на всю глубину проплавления [16]. Форму полости фиксировали путем резкого прекращения процесса сварки отключением ускоряющего напряжения.

Математическое моделирование распределения энергии электронного пучка. На рис. 3 представлена схема электронно-лучевой сварки при сканировании в виде растра. Форма получаемого при этом шва имеет почти параллельные стенки и значительный радиус в корне, позволяющий устранить корневые дефекты, в 3–4 раза уменьшилась нестабильность глубины проплавления. Открытость и устойчивость полости проплавления приводит к дегазации сварочной ванны и снижению пористости. За счет снижения доли энергии, затрачиваемой на испарение материала, повышается проплавляющая способность процесса ЭЛС [1].

Эффект образования полости проплавления целесообразно исследовать при сварке различных материалов и разных толщин. Для этого должна быть создана аппаратура, реализующая сканирование в виде различных растров. В данной работе рассматривается три вида сканирования: классический растр, синусоидальный растр и усеченный растр. Задача этого исследования заключается в получении плотности распределения энергии сканирующего электронного пучка на поверхности детали по пятну нагрева. Она характеризует распределение энергии в сварочной ванне.

Распределение энергии в электронном пучке обычно описывается нормальным законом, который характеризуется плотностью вероятности вида [17]

г, х        1      * f ( x - m ) ²

f ( x ) =----== * exp -                                 z ])

а*x2*n     (  2*a2 J,                          (1)

где x - координата по оси абсцисс; m - математическое ожидание; с - среднеквадратичное отклонение, характеризующее диаметр электронного пучка, концентрацию энергии в нем. Эта величина определяется электронно-оптической системой пушки и ее фокусирующей системой. Она зависит от тока сварки и обычно определяется в пределах с = 0,05 - 0,5 мм. Чем меньше диаметр электронного пучка, тем более качественный пучок формирует пушка.

Для того чтобы при построении характеристик плотности распределения энергии по пятну нагрева не учитывать конкретное значение среднеквадратичного отклонения, введем безразмерные координаты и амплитуды сканирования пучка по этим координатам:

У = -, а где у - координата вдоль стыка; с - среднеквадратичное отклонение; у - безразмерная координата вдоль стыка. В системе безразмерных координат с = 1;

x = -,                                         (3)

а

где x - координата поперёк стыка ; x - безразмерная координата поперёк стыка;

A = ^A ,                                       (4)

а

где A – амплитуда4 A – безразмерная амплитуда.

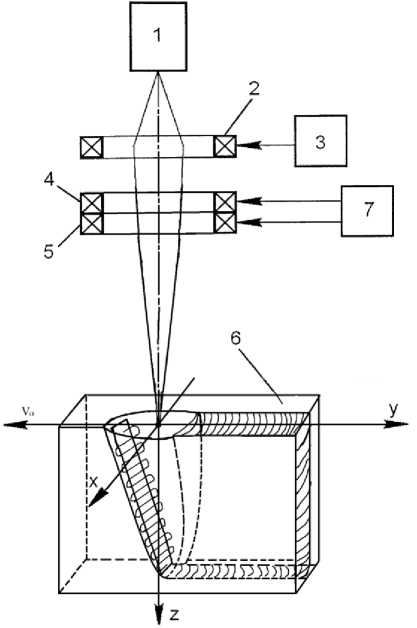
Рис. 3. Схема электронно-лучевой сварки при сканировании в виде растра:

1 – электронно-лучевая пушка; 2 – фокусирующая система; 3 – источник тока фокусировки; 4 и 5 – отклоняющая катушка; 6 – поверхность изделия; 7 – генератор сканирования пучка

Fig. 3. A scheme of electron-beam welding during scanning in the form of a raster:

1 – electron beam gun; 2 – focusing system; 3 – focus current source; 4 and 5 – deflection coil; 6 – product surface; 7 – beam scan generator

Известно, что максимальная ордината нормального распределения (1), равная, соответствует точке x = m. По мере удаления от точки m плотность распределения падает. Центром симметрии распределения является центр рассеивания m . Это ясно из того, что при изменении знака разности (x – m) на обратный, выражение (1) не меняется. Если изменять центр рассеивания m , кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы. Центр рассеивания характеризует положение распределения на оси координат [9]. Поэтому, изменяя центр рассеяния по соответствующему закону, можно получить плотность распределения энергии по соответствующей координате.

Энергия электронного пучка [18]

W ( x , y ) = U * I * ∫^∞ ∫^∞ W ( x ) W ( y ) dxdy ,                            (5)

-∞-∞ где U – ускоряющее напряжение; I – ток луча; W(x) и W(y) – нормированные функции ∞∞ распределения энергии по соответствующим координатам; ∫W(x)dx = 1; ∫W(y)dy = 1 .

-∞             -∞

Далее рассмотрим каждое сканирование подробнее. При сканировании в виде классического растра движение по координате поперёк стыка осуществляется по двухсторонней пиле, описываемой кусочно-линейной функцией:

x = k * t + m,                                          (6)

где t – независимая переменная; k и m – некоторые числа, а при условии, что k = 1 за время t = [–1;1] при периоде T , данный график будет в виде треугольной функции (рис. 4).

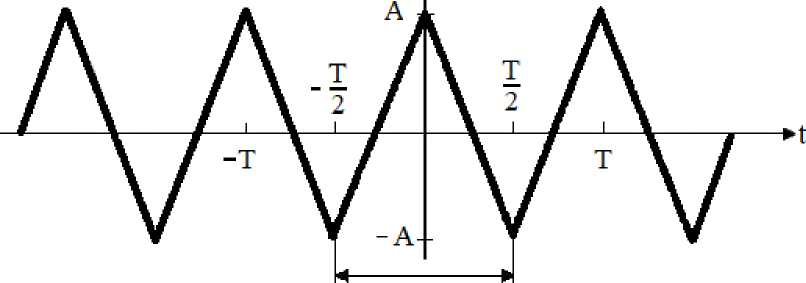
Рис. 4. График последовательных треугольных импульсов

Fig. 4. Graph of successive triangular pulses

Известно, что при изменении математического ожидания в формуле (1), смещается график относительно его центра. Следовательно, вместо математического ожидания можно подставить необходимое нам выражение, для растра – это линейная функция. Так же необходимо проинтегрировать полученное выражение. Получим следующую формулу [18]:

W ( x ) = J

- 1

ст*V2*n

Г

*exp •

V

(x-(ax *k*t + m))2 2*ct 2

dt ,

где A e [1;10], x e [-15;15]; k = 1; m = 0; x - безразмерная координата вдоль стыка; A_x -безразмерная амплитуда поперёк стыка; с - среднеквадратичное отклонение.

На рис. 5 показана фигура при нормальном распределении энергии для случая траектории сканирования электронного пучка в виде растра поперёк стыка.

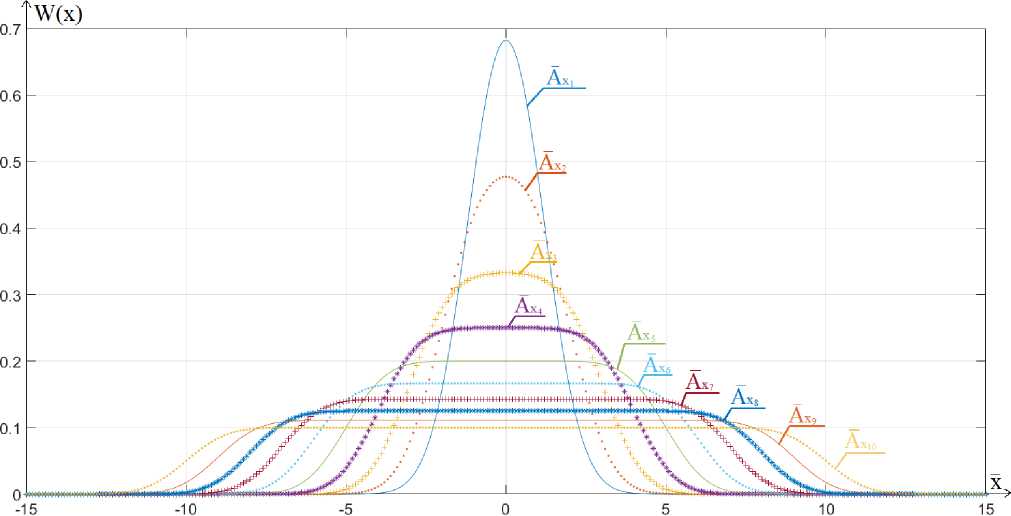
Рис. 5. Распределение энергии пучка на поверхности детали при растровом сканировании:

А = 1 ; A X 2 = 2 ; A 3 = 3 ; A 4 = 4 ; A 5 = 5 ; A 6 = 6 ; A 7 = ⁷ ;     = 8 ; A 9 = 9 ; Х = 10

Fig 5. Energy distribution on the surface for the case of a scanning trajectory in the form of a truncated raster:

A = 1   A v = 2 A v = 3 А =4 А =5 Д =6 A v = 7 A = 8 A =9 A =10

^X 1           ^x 2      •    ^x 3         A x 4       • A x 5   ⁵. A x 6     ^{6     x} 7           ^x 8         A x 9    ⁹ • A x 10     ¹⁰

;                          ;                         ;                          ;                        ;                         ;                          ;                         ;                         ;

На рис. 6 показана траектория сканирования электронного пучка в виде усеченного растра. Траектория сканирования в виде растра описывается формулой (8), но добавляются дополнительные ограничения в виде следующей системы [18]:

A = 1, при t e [ 0.7;1.2 ]

{

A = - 1, при t e [ 2.6;3.2 ]

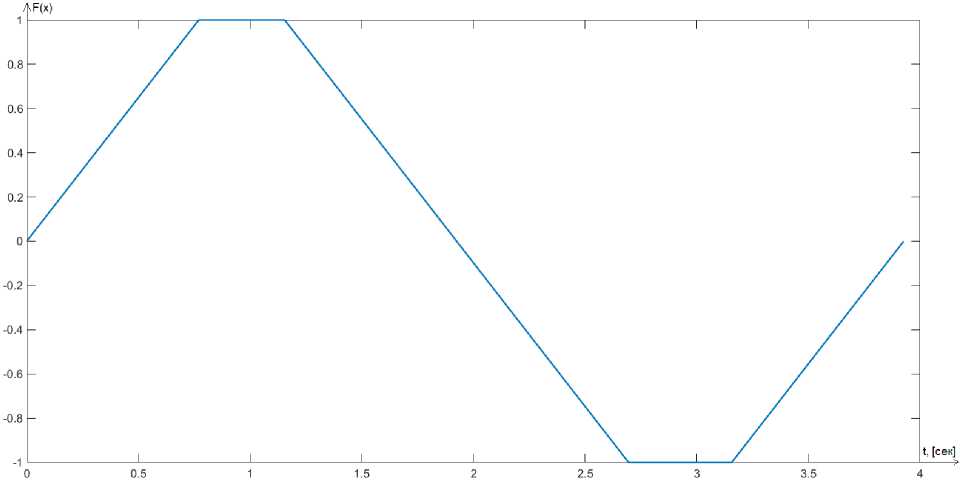
Рис. 6. Форма управляющего сигнала в виде треугольника с зонами насыщения

Fig. 6. The shape of the controlling signal in the form of a triangle with saturation zones

При сканировании усеченным растром на определенных участках при определенном периоде, амплитуда принимает фиксированное значение. Поэтому в формулу (7) добавим выражения, с помощью которых описываются пики, возникающие на значениях равных амплитуде. Получим следующее выражение:

W ( x ) =

T — 2* M

T

*

J

- 1

ст *42* л

* exp

⁽ x ~ ( A x * k * t + m ) ) ² 2* ст ²

M dt +--

T

(   ( exp к   v

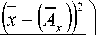
2* ст ²

+ exp

—

к

⁽ x ^{+ (} A x ) ) ² 2* ст ст

, (9)

где x – безразмерная координата поперёк стыка; A – безразмерная амплитуда поперёк стыка; с — среднеквадратичное отклонение; m = 0; к = 1; M - время насыщения; T - период сканирования.

В формуле (9), при амплитуде равной 3 и при условии, что площадь фигуры при нормальном распределении энергии, изменим пределы границ зоны насыщения ^ = [ 0.05;0.1;0.15;0.2;0.25;0.3;0.4 ] и получим следующие кривые распределения энергии, показанные на рис. 7.

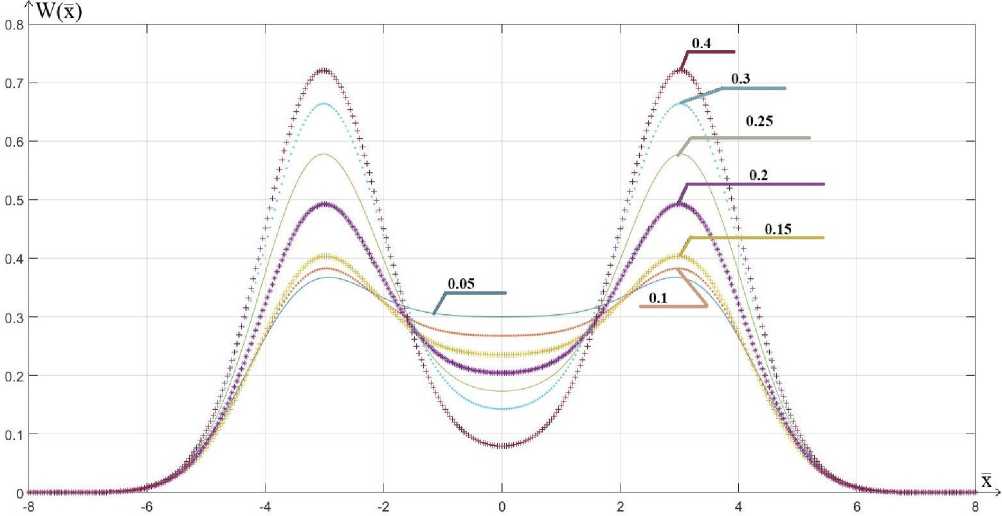
Рис. 7. Распределение энергии пучка на поверхности детали при сканировании усеченным растром и изменении границ зоны насыщения

Fig. 7. Energy distribution when changing the limits of the saturation zone

Из полученных графиков видно что, изменяя величину зоны насыщения М можно регулировать амплитуду двухгорбового распределения энергии по пятну нагрева и этим добиваться наилучшей формы сварного шва. Чтобы воспользоваться полученными расчетными характеристиками, необходимо перейти от безразмерных координат к размерным координатам. Для этого необходимо провести следующие действия [18]:

y = y * a ; x = x * c ; A = A * a ; W ( x ) = W ⁽ x ) ; W ( y ) = W ⁽ y ) . ст            a

В результате проведенных исследований была разработана программа для управления распределением энергии по пятну нагрева с помощью использования различных разверток [19].

Заключение. Можно сделать следующие выводы:

• 1.    Для исследований по оптимизации процесса электронно-лучевой сварки целесообразно использовать сканирования электронного пучка в виде растра, позволяющего получить устойчивую полость проплавления и высокое качество сварных соединений.

• 2.    Форма сканирования в виде усеченного растра позволяет получить двухгорбовое распределение энергии по координате поперек стыка, которое необходимо для формирования сварного шва с параллельными стенками и значительным радиусом в корне, исключающим появление корневых дефектов.

• 3.    Численное моделирование тепловых процессов для определения параметров ЭЛС позволит существенно сократить затраты на отработку технологий для конструкций из новых материалов и различных толщин.