Особенности модуляции космических лучей в минимуме 24-го солнечного цикла

Для описания модуляционных эффектов космических лучей (КЛ) в гелиосфере принципиально возможны два подхода. Согласно первому из них модуляция КЛ обусловлена изменением плотности частиц за счет их выноса мелкомасштабными магнитными неоднородностями, вмороженными в плазму солнечного ветра (СВ), и диффузией вдоль спирального межпланетного магнитного поля (ММП) [Parker, 1963]. Амплитуда модуляции в линейном приближении пропорциональна скорости СВ, размеру области модуляции и обратно пропорциональна коэффициенту диффузии. Анизотропия в распределении частиц по направлениям прихода мала и в основном имеет токовую структуру [Крымский, 1969].

В соответствии со вторым подходом предполагается, что ММП в большей степени структурировано, чем турбулизовано. Определяющим фактором в модуляции КЛ является изменение их энергии при движении в регулярных электромагнитных полях гелиосферы. Изменение же энергии, в свою очередь, определяется величиной и природой электрических полей межпланетной среды и временем взаимодействия частиц с этими полями [Dvornikov, Sdobnov, 2002], которое в значительной мере определяется структурами ММП типа магнитных ловушек. Анизотропия КЛ может достигать значительной величины и, наряду с первой, иметь более высокие гармоники [Dvornikov et al., 1983; Richardson et al., 2000].

Минимум между циклами солнечной активности 23 и 24 был необычно продолжительным и глубоким [ftp://ftp.ngdc.noaa.gov/STP/SOLAR_DATA/SUN SPOT_NUMBERS/]. Этот период, названный в работе [Базилевская и др., 2011] минимумом цикла 24, характеризуется минимальным за последние несколько солнечных циклов сглаженным числом солнечных пятен R z . В работе [Базилевская и др., 2011] отмечается, что магнитное поле солнечных пятен систематически уменьшается с 1992 г. независимо от фазы цикла [Livingston, Penn, 2009]. Магнитное поле Солнца как звезды тоже уменьшилось. В мае 2009 г. оно составляло 3.6 мкТл, тогда как в предшествующие минимумы активности было ~6–7 мкТл [ftp://ftp.ngdc.noaa.gov/STP/SOLAR_DATA/SUN_AS

_A_STAR/]. Так как магнитные поля на Солнце являются источником гелиосферного магнитного поля, то оно тоже ослабло и на орбите Земли в 2009 г. неоднократно опускалось ниже 4 нТл. Это на ~1 нТл ниже, чем в предшествовавшие минимумы активности []. В связи с этим наблюдаемые потоки галактических КЛ достигли самого высокого уровня за весь период, в течение которого проводились регулярные измерения космического излучения [Свиржевская и др., 2010]. Так, например, по данным наблюдений на ст. Иркутск (435 м над уровнем моря) интенсивность нейтронной компоненты КЛ в октябре 2009 г. повысилась на ~2 % по сравнению с апрелем 2008 г. По-видимому, природа данного явления аналогична природе эффекта, описанного в работе [Базилевская и др., 2011], где показано, что в минимуме между 23-м и 24-м циклами солнечной активности модуляция потоков КЛ была минимальной за весь период прямых наблюдений КЛ. В настоящей статье по наблюдениям интенсивности КЛ на мировой сети станций и на космическом аппарате GOES на основе предположения, что определяющим фактором в модуляции КЛ является изменение их энергии при движении в регулярных электромагнитных полях гелиосферы, проведены расчеты дифференциального жесткостного спектра КЛ на орбите Земли в апреле 2008 и октябре 2009 г.

Модуляция космических лучей регулярными электромагнитными полями межпланетной среды

Для описания модуляционных эффектов в рамках второго подхода использовалось кинетическое уравнение в дрейфовом приближении без учета эффектов выноса КЛ мелкомасштабными магнитными неоднородностями, вмороженными в плазму СВ, и диффузией частиц вдоль спирального ММП. Следует отметить, что данное приближение не исключает наличия рассеяния частиц на магнитных неоднородностях, но предполагает, что этот процесс не является марковским. В этом случае возможна ситуация, когда при ненулевом среднеквадратичном отклонении частиц в угловых и пространственных координатах их средние отклонения будут близки нулю. При таком характере рассеяния необходимо учиты- вать эффекты, накапливающиеся при многократном вращении частиц по ларморовской окружности, т. е. использовать дрейфовое приближение, пренебрегая эффектами конвекции и диффузии. В данном случае изменение интенсивности КЛ в гелиосфере происходит вследствие изменения энергии в регулярных электромагнитных полях межпланетной среды в соответствии с теоремой Лиувилля, которая в дрейфовом приближении имеет следующий вид [Сиву-хин, 1963]:

d F   , FF   . FF  .5 F  _n

--+ r--+ p.. — + p,---= 0, dt    dr     dp^      dp где c         1 cp v r = v h + — E x B +---- x || B2          2 z B

.V x h(hV x h) + h x---

B cp- h x (hV)h. zeB

cp p„ = zeEh + - v- p - Vh + 4 Eh x (hVh) —

2 B

—

cp.p, v, VB ,

^{- -} ---h x ( h V ) h + h Vx ( h V ) h .

B

2 z _e B

P i"v- PVh — cP -

2 B

h Vx E — Eh x-- Eh ( h V ) x h B

₊ cp,p - ^v

2 z B e

— h x (hV )h + hVx (hV)h B pil, у| и p±, v- - составляющие импульса и скорости частиц, параллельные и перпендикулярные вектору магнитного поля; ze – их заряд; с – скорость света; h – единичный вектор в направлении поля В; r – пространственный вектор; t – время.

Отметим, что функция распределения F относится не к распределению самих частиц, а к распреде- лению их ведущих центров.

При стационарном и пространственно-однородном СВ радиальная и азимутальная компоненты ММП имеют вид [Parker, 1963]

B r ( r) = B r ( r ₀)

Вф (r, !)=Br (r) — sinZ, u где u - скорость СВ, Q - угловая скорость вращения

Солнца, а индуцированное электрическое поле

E = — - u x B .

c

С учетом (2)–(4) и (5), (6) из (1) получим уравнение (в переменных r , p , ц ), описывающее влияние регулярных полей СВ на функцию распределения КЛ в межпланетном пространстве F ( r , p , ц ):

2    Q vR vц cos T + и sin T +----x

_                    uB x cos Xcos T sin2 T (ц2 — 1) 1 —

^J d r

1 vR ....... _22x d f

+--- sin T cos T (1 + cos T )(1 + ц ) — +

2 B0 r0                                 dX

1 v

+ — cos T (1 + cos T )(1 — ц ) x

2r df   1 u        4         2

x----(1 — cos T)(1 + ц )p— = 0, дц 2 rd где μ=cosθ, θ – питч-угол частицы в ММП;

( Q r sin A A

T = arctan I ------- I - угол между радиусом и си-

V и )

ловой линией ММП.

При изменении структуры поля соответствующим образом изменятся и выражения перед частными производными в данном уравнении и, следовательно, изменится вид функции распределения частиц. Таким образом, в предлагаемом подходе к проблеме модуляции КЛ вариации функции распределения частиц отражают изменения в структуре электромагнитных полей межпланетной среды.

При движении в электромагнитном поле (5), (6) заряженные частицы космического излучения, наряду с движением вдоль поля и дрейфом под действием силы z _e E , будут дрейфовать в направлении, обратном направлению электрического поля, и в результате этого терять часть своей кинетической энергии. Дрейф в указанном направлении обусловлен двумя причинами: во-первых, кривизной силовых линий (центробежный дрейф) и, во-вторых, наличием нормальной по отношению к силовой линии компоненты градиента поля (магнитный или градиентный дрейф).

Изменение жесткости частицы R за счет данного процесса описывается уравнением [Дворников, Матюхин, 1976]

ddR . 2 Ur ( 1 — cos¹ T )( 1 + ц ² ) .                (8)

Для решения уравнения (7) произведем замену переменных в уравнении (8).

В связи с тем, что изменение энергии происходит вследствие центробежного и градиентного дрейфа по координате X антипараллельно индуцированному электрическому полю, в (8) можно перейти от переменной t к переменной X :

dR Z= — ¹ R- (1 — cos¹ v)(1+H 2 ).             (9)

d λ2 r

1 vR

X =--sin T cos T x

2 B 0 r 0 ²

x (1 + cos² T )(1 + ц 2 ).

С учетом (10) уравнение (9) примет вид

Особенности модуляции космических лучей в минимуме 24-го солнечного цикла pdp

2    2,2

V c Р + ^E 0

Z e ^ B 0 Г

c

sin XdX.

Проинтегрировав (11) по λ, получим

z ^Bnr2

A e =--------- (1 - cos X_E ) = z U,

c

где U =Ω B ₀ r ₀²(1–cosλ _E ) – потенциал электрического поля (6) на гелиошироте X_E.

Выражение (12) показывает, насколько изменится энергия частицы при дрейфе от полюса до плоскости гелиоэкватора.

Из уравнения (12) следует, что потери энергии частиц при потенциальном электрическом поле не зависят от жесткости частиц и при характерной напряженности ММП ( ~ 5 нТл) составляют ~ 200 МэВ.

В том случае, когда ММП имеет структуру, отличную от спиральной (например, при наличии петлеобразных структур или магнитных облаков, т. е. магнитных ловушек), значения ∆ε будут зависеть от напряженности магнитных полей данных структур и скорости СВ и почти на порядок превосходить 200 МэВ [Dvornikov, Sdobnov, 2002].

В соответствии с предлагаемой концепцией, если жесткостной спектр в Галактике описывается степенной функцией от жесткости частиц R , то из условия J ( R )/ p ²=const следует, что жесткостной спектр в гелиосфере будет иметь следующий вид:

J(R) = A (e2 -О" ^ -', (13) e[(e + Ae) -e0](T + e0 )

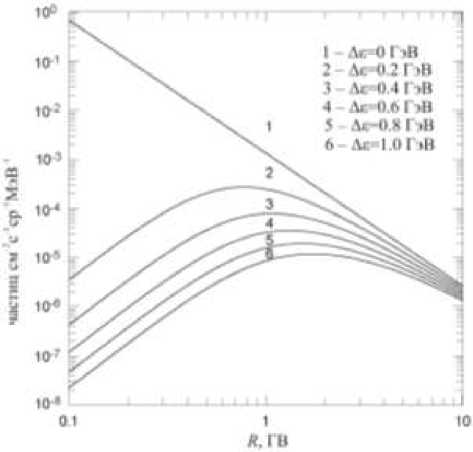
Рис. 1. Расчетные спектры КЛ при различных значениях Δε.

где £ - полная энергия частиц с жесткостью R ; Аб -ее изменения в электромагнитных полях гелиосферы; £ 0 - энергия покоя; T 0 - кинетическая энергия частиц, при которой интенсивность КЛ соответствующей жесткости в Галактике равна А ; А и у -спектральные индексы галактического спектра.

Полученное выражение удовлетворяет кинетическому уравнению в дрейфовом приближении, т. е. теореме Лиувилля. Это легко проверяется подстановкой выражения для жесткостного дифференциального спектра (13), с учетом (12), в уравнение (7). На рис. 1 представлены расчетные спектры КЛ при различных значениях Δε, соответствующих наблюдаемым значениям модуля ММП и скорости СВ, полученные с использованием выражения (13).

ции отсчитывались от спокойного уровня апреля 2008 г.

Для определения зависимости Аб от R методом минимизации функционала с               ,         ’/2                а2

5 = El J(R - A  (e2-eo)____(£+Ae 1  >

k [ k    £[(e + Ae)2-E2](T + e0 )

решалось уравнение (13) путем подстановки наблюдаемых значений интенсивности частиц в левую часть уравнения для каждого из используемых интервалов энергий с целью определения неизвестной величины Аб , соответствующей данному энергетическому интервалу. В результате были определены зависимость Аб от жесткости частиц, соответствующей среднему значению энергии в используемых интервалах энергии, т. е. Аб ( R ), и жесткостной спектр протонов на орбите Земли в апреле 2008 г. и октябре 2009 г. На рис. 2 представлены часовые значения изменения энергии КЛ в электромагнитных полях гелиосферы в апреле 2008 г. и в октябре 2009 г.

Результаты и выводы

В настоящей работе использованы данные наблюдений интенсивности протонов на спутнике GOES-11 в энергетических диапазонах 4–9, 9–15, 15–40, 40–80, 80–165 и 165–500 МэВ [ ]. При более высоких энергиях использовалась информация о вариациях первичного спектра КЛ, полученная методом спектрографической глобальной съемки (СГС) [Dvornikov, Sdobnov, 1997; 2002] по наземным измерениям на мировой сети нейтронных мониторов (44 станции). Амплитуды модуля-

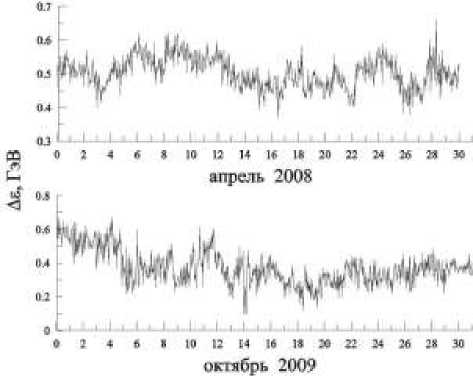
Рис. 2. Изменения энергии КЛ в электромагнитных полях гелиосферы в апреле 2008 г. и в октябре 2009 г.

Я, MB

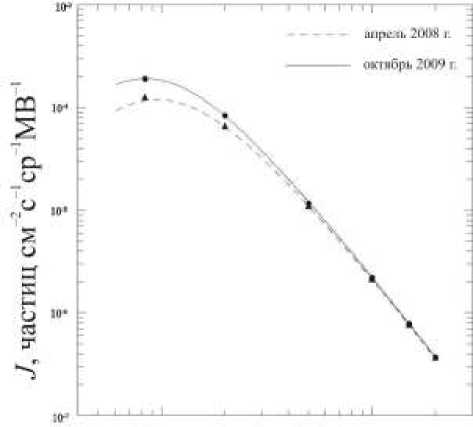
Рис. 3. Дифференциальные спектры протонов на орбите Земли в апреле 2008 г. и октябре 2009 г.

Изменения энергии КЛ в электромагнитных полях гелиосферы в апреле 2008 г. в среднем составили ~0.50 ГэВ, а в октябре 2009 г. – ~0.37 ГэВ. Эти величины близки значениям модуляционного параметра для периодов минимума солнечной активности, полученным в работе [Usoskin et al., 2005] на основе модели силового поля (force field model) [Glesson, Axford, 1968]. Результаты расчетов жест-костного спектра протонов показаны на рис. 3, где штриховая кривая – жесткостной спектр протонов в апреле 2008 г., сплошная – в октябре 2009, треугольники и кружки – данные наблюдений.

Видно, что результаты расчетов хорошо соответствуют данным наблюдений мировой сети станций космических лучей, а изменения энергии КЛ в электромагнитных полях гелиосферы в апреле 2008 г. и октябре 2009 г. не противоречат значениям модуляционного параметра для периодов минимума солнечной активности, полученным на основе модели силового поля.

Из вышеизложенного можно сделать вывод о том, что определяющим фактором увеличения потоков галактических КЛ на орбите Земли в октябре 2009 г. по сравнению с апрелем 2008 г. является уменьшение потерь энергии при движении частиц в регулярных электромагнитных полях гелиосферы.

Данная работа поддержана программой Президиума РАН «Фундаментальные свойства материи и астрофизика» в рамках проекта «Космические лучи в гелиосферных процессах по наземным и стратосферным наблюдениям».