Особенности обработки широкополосных сигналов при воздействии преднамеренных помех, соизмеримых с полезным сигналом по полосе частот
Автор: Габриэльян Дмитрий Давидович, Новиков Артем Николаевич, Стрекалов Анатолий Васильевич, Шацкий Виталий Валентинович, Шацкий Николай Витальевич
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Электромагнитная совместимость и безопасность оборудования
Статья в выпуске: 3 т.9, 2011 года.
Бесплатный доступ
Рассмотрен метод квазиоптимальной обработки широкополосных сигналов в условиях помех. При- ведены аналитические выражения для оптимальной частотной зависимости весовых коэффициентов в соответствии с критерием минимизации средне- квадратического отклонения в полосе частот. Раз- работаны предложения по технической реализации обработки широкополосных сигналов путем форми- рования квазиоптимальной частотной зависимости вектора весовых коэффициентов. Проанализировано влияние различных видов аппроксимации частотной зависимости на величину среднеквадратического отклонения сигнала в полосе частот. Представлены результаты численного моделирования.
Оптимальная частотная зависимость, квазиоптимальная частотная зависимость, широкополосный сигнал, весовой коэффициент, спектр сигнала, адаптивная антенная решетка
Короткий адрес: https://sciup.org/140191497
IDR: 140191497 | УДК: 621.396.677
Текст научной статьи Особенности обработки широкополосных сигналов при воздействии преднамеренных помех, соизмеримых с полезным сигналом по полосе частот
Обширный круг задач, решаемых современными телекоммуникационными системами, требует внедрения новых технологий и принципиально новых возможностей. Основными областями применения телекоммуникационных систем являются радиолокация, радиоразведка, телевидение, включающие устройства приема и передачи информации для организации информационного обмена. Следует отметить, что прием полезного сигнала в реальных условиях всегда затруднен вследствие наличия естественных и преднамеренных помех. Обработка полезного сигнала производится в линейных и нелинейных цепях, носит комплексный характер и связана с демодуляцией, фильтрацией, задержкой во времени и другими преобразованиями сигнала. Возрастает роль цифровой обработки сигналов, которой занимаются ведущие организации мира. Исходя из вышесказанного, выбор метода оптимальной обработки принятого полезного сигнала играет одну из важнейших ролей при решении проблемы обеспечения информационной безопасности систем связи, что требует применения новых средств и методов, позволяющих обеспечить защиту каналов информации на качественно новом уровне, например с использованием адаптивных методов.
Постановка задачи
Для качественной оценки процесса обработки принятых дискретных сигналов обычно используют вероятность ошибки принятого символа в зависимости от отношения мощностей сигнал/ помеха на входе приемного устройства. Поэтому большинство существующих методов обработки основано на использовании критерия минимизации среднеквадратического отклонения или максимизации отношения «сигнал / (помеха+шум)». Выбор критерия обработки во многом обусловлен формой полезного сигнала и законом распределения помехи. На основе анализа литературных источников можно сделать вывод, что сформулированная проблема достаточно хорошо решена теоретически и практически для узкополосных сигналов [1-3], например, путем формирования «нулей» диаграммы направленности (ДН) за счет подстройки комплексных весовых коэффициен- тов в каналах обработки адаптивной антенной решетки (ААР). Однако при широкополосных полезном и помеховом сигналах комплексный весовой коэффициент для каждого канала ААР, обеспечивающий подавление составляющей помехи на некоторой частоте а>х, не будет таковым для составляющей на частоте со,, так как «нули» ДН антенной решетки смещаются или исчезают при изменении частоты. Трудность заключается в том, что при подавлении широкополосных помех приходится реализовывать формирование «нуля» ДН в заданном направлении в требуемом спектре частот.
Описание алгоритма обработки.
Рассмотрим N-элементную ААР с известной геометрией излучающего раскрыва, осуществляющую прием полезного сигнала с направления 9».ф» и подавление широкополосных помех, приходящих с неизвестных направлений 0 , <р
LY
Требуется определить и реализовать набор частотно- зависимых весовых коэффициентов в каналах ААР, обеспечивающих минимум среднеквадратического отклонения спектров полезного сигнала и выходного сигнала антенны в полосе частот обработки.
Обобщая критерий минимизации среднеквадратической ошибки для узкополосного сигнала [1] на случай широкополосного сигнала, получим соотношение вида:
™2
52 = min
У L 2
^C^^-^W1 (со)Х(_со") da>
-»2
-1
, (1)
где ^„(6)) спектр полезного сигнала; Х(со) спектр суперпозиции сигналов на выходах излучателей; W(ro) – частотно-зависимый вектор весовых коэффициентов в каналах обработки ААР; сох,..со, – частоты, определяющие полосу частот, в которой обрабатывается полезный сигнал.
Минимальное значение интеграл (1) принимает, если подынтегральное выражение будет минимальным на каждой из указанных частот. С учетом данного утверждения на основании результатов работы [1] представим частотную зависимость весовых коэффициентов в виде
^„Дсо) = М-Чю)8До)), (2)
где М^ЧД – частотно-зависимая обратная ковариационная матрица помеховых сигналов;
5ЧД = exp(-i6)4^A(x„ sin 6>0 cos^0 + + Z,sin6'0sin^0))
– управляющий вектор, обеспечивающий построение заданной ДН; £«, А„ – электрическая и магнитная постоянные свободного пространства; 0^ФО – углы направления прихода полезного сигнала; ^ n ^ У и – координаты n -го элемента ААР.
При произвольном числе помеховых сигналов частотно-зависимая ковариационная матрица помеховых сигналов определяется соотношением мн = ст2е + £ |с, (®)р; пи; и, (з)
где сг – мощность тепловых шумов антенной решетки; С; (а>) – спектр l -го помехового сигнала, 1 = 1,...,L;
Utn = exp^-ica^jEtljUtl (хп sin 6 cos#?, +
+ Х sin 6, sin ф^ – вектор-столбец, элементами которого являются комплексные сомножители, учитывающие фазовый набег на каждом элементе антенной решетки.
Обратная частотно-зависимая ковариационная матрица с использованием (2) записывается в следующем виде:
м-' п=Me _ у^а,р пи; пи; п СГ /=1 Р=1
• (4)
В (4) известны все члены за исключением частотно-зависимых коэффициентов «л®^ которые можно найти из (3) и (4) по условию АГ' ИМИ = Е • Выражение для частотно-зависимого вектора весовых коэффициентов имеет вид:
^и=А^£-ЕЕ^х<у)х _ xu;nu;n^s*n
После проведения математических преобразований выражения (5) с учетом соотношений для S^ ((У) и Ut (ty) получим аналитическую зависимость вектора весовых коэффициентов от частоты. Однако точно реализовать данную зависимость технически невозможно. Поэтому предлагается обеспечить близкую к точной реализацию значений вектора весовых коэффициентов в полосе частот полезного сигнала для ограниченного числа M частот из данного частотного ин- co,- co, тервала, ширина которого равна .
Между данными частотами значения весовых коэффициентов могут быть аппроксимированы достаточно простой зависимостью, например, кусочно-постоянной функцией:
w^^w^M,
(«)
L
0,
|(У-(У,""|<А/2,
I A ^^ m – среднее зна-
\(D-COU"'\>^1.
чение m -го частотного интервала; m = \,...,M ;
или кусочно-линейной функцией:
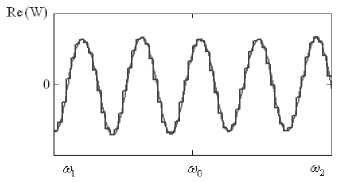
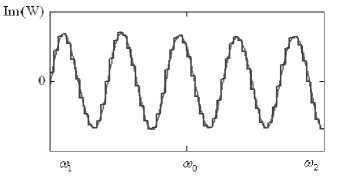
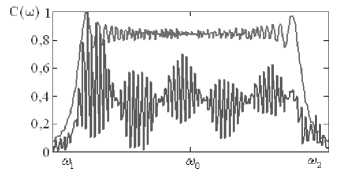
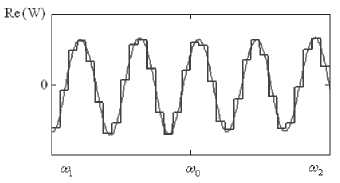
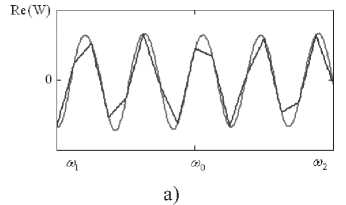
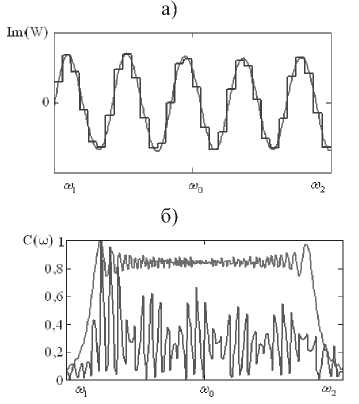
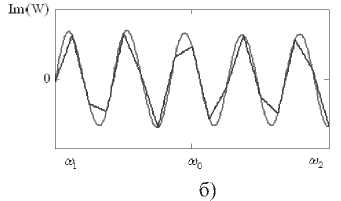
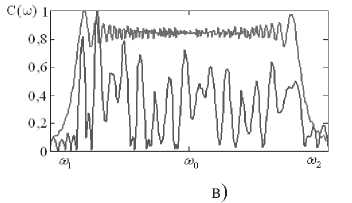
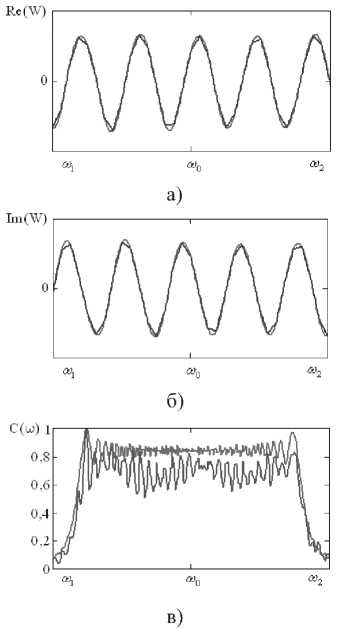
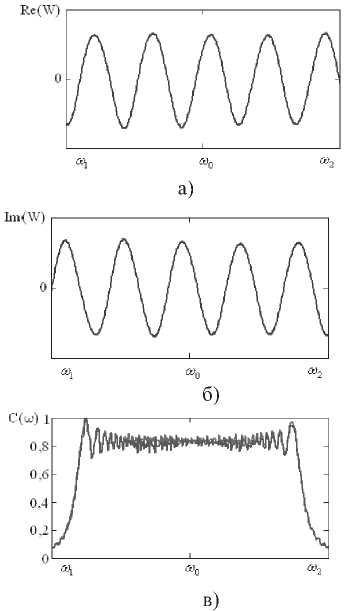
wn = ^—-—W(®„J( ' m+1 m V / -^HXco-to, „„)}. Исходя из полученных закономерностей, проведем сравнительный анализ зависимости восстановления спектра полезного широкополосного сигнала в присутствии различных помех от вида аппроксимации частотно-зависимого вектора весовых коэффициентов в заданной полосе частот. Результаты численных исследований Для исследования возникающих закономерностей рассмотрим антенную решетку 10x5 ( ^ = 50), элементы которой расположены с шагом 0,52 (X – длина волны, соответствующая средней частоте диапазона полезного сигнала). Сигнально-помеховая обстановка характеризуется направлением прихода полезного сигнала 0й=жфй=^с базой В = 200, широкополосного помехового сигнала – 0x = 45°, фх - 0° . Результаты исследований влияния числа интервалов M на нормированную величину среднеквадратической ошибки восстановления спектра полезного сигнала, определяемую выражением (1), при различных видах аппроксимации приведены на рис. 1-6. На всех рисунках а) и б) приведены действительная и мнимая части весового коэффициента в 9-ом излучателе, а на рисунках в) – восстановленные спектры широкополосного полезного сигнала, причем тонкой кривой показана оптимальная обработка, а утолщенной – квазиоптимальная. На рис. 1-3 в) приведены спектры сигналов после квазиоптимальной обработки для 16, 32 и 64 частотных интервалов. При кусочно-постоянной аппроксимации нормированное среднеквадратическое отклонение спектра восстановленного широкополосного сигнала от спектра полезного сигнала без воздействия помехи для данных частотных интервалов равно 0,495; 0,481 и 0,332 соответственно, а для кусочно-линейной аппроксимации этот показатель равен 0,388; 0,039 и 1,12-10" . Отсюда можно заключить, что использование кусочно-линейной аппрок- симации значительно уменьшает нормированное среднеквадратическое отклонение спектра восстановленного широкополосного сигнала от спектра полезного сигнала без воздействия помехи. Рис. 1. Восстановление спектра сигнала при кусочнопостоянной аппроксимации для М = 16 Рис. 3. Восстановление спектра сигнала при кусочнопостоянной аппроксимации для М = 64 Рис. 4. Восстановление спектра сигнала при кусочнолинейной аппооксимании для М = 16 в) Рис. 2. Восстановление спектра сигнала при кусочнопостоянной аппроксимации для М = 32 Рис. 5. Восстановление спектра сигнала при кусочнолинейной аппроксимации для М = 32 Рис. 6. Восстановление спектра сигнала при кусочнолинейной аппроксимации для М = 64 Заключение Проведенные исследования показывают, что при меньшем числе частотных интервалов при кусочно-линейной аппроксимации вектора весовых коэффициентов возможно достижение более точного восстановления спектра широкополосного полезного сигнала, что несомненно приведет к упрощению адаптивной антенной решетки.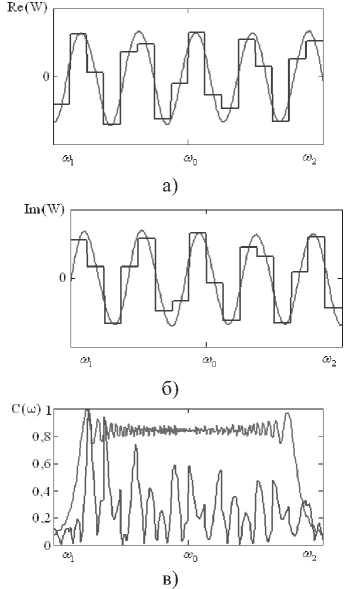
Список литературы Особенности обработки широкополосных сигналов при воздействии преднамеренных помех, соизмеримых с полезным сигналом по полосе частот
- Монзинго Р.А., Миллер Т.У. Адаптивные антенные решетки. Введение в теорию. Пер. с англ. М.: Радио и связь, 1986. -448 с.
- Литвинов О.С. О теории адаптивных антенных решеток в условиях коррелированных по-меховых сигналов//Антенны. Под ред. А.А. Пистолькорса. М.: Радио и связь, вып. 29, 1981. -С. 67-79.
- Литвинов О.С. Аналитические свойства ковариационной матрицы помех в теории прием-ных адаптивных решеток//Антенны. Под ред.А.А. Пистолькорса. М.: Радио и связь, вып. 30. 1982. -С. 65-78.


