Особенности обработки спектров окрашенных суспензий в кюветах с толстыми стенками

В последние десятилетия возрос интерес к использованию методов спектроскопии для исследования различных светорассеивающих систем. К наиболее важным применениям данной группы методов относятся идентификация подлинности документов [1], определение качества продуктов питания [2], семян [3] и листьев [4], оценка концентрации биологически активных веществ в крови [5] и новообразований злокачественного характера в организмах [6– 10]. Можно выделить две основных стратегии при решении подобных задач:

• 1.    Построение калибровочной зависимости на основе большой совокупности исходных данных [7].

• 2.    Разработка модели переноса излучения в объекте с численным решением обратной задачи [5].

Второй вариант решения использовался для получения спектров поглощения и рассеяния образцов на основании измеренных данных по диффузному отражению и пропусканию при обработке в рамках модификаций теории Кубелка–Мунка [11] и инверсного метода Монте–Карло [9]. При решении всех задач данного класса необходимо не только использовать эффективные методы теории переноса излучения, но и учитывать особенности измерительной системы. С этой целью в [12] было исследовано влияние стеклянной пластины, накрывающей поверхность порошкообразного образца, на результаты измерения коэффициентов диффузного отражения. В [13] было рассмотрено влияние отражений света от стекол, между которыми помещался образец биологической ткани, на определяемые величины коэффициентов диффузного отражения и пропускания в рамках диффузионного приближения. Корректировка коэффициентов коллимированного пропускания с учётом многократ- ного отражения в кюветной стенке приведена в [13]. Аккуратный учёт экспериментальных особенностей необходим при решении обратных задач. Особенно остро данная проблема возникает при исследовании образцов одновременно поглощающих и рассеивающих электромагнитное излучение, когда погрешности измерения могут привести к завышению показателя поглощения. Цель настоящей работы: учёт влияния условий измерения на оптические свойства в предельном случае кюветы с толстыми стенками и верификация на примере модельной суспензии.

1.    Методика моделирования

В настоящей работе использовались основные элементы расчёта коэффициентов пропускания и отражения плоскопараллельного слоя, применённые в [4–16] для оценки оптических свойств композитов прозрачная матрица-наночастицы металлов [17]. Применялось одномерное уравнение переноса излучения [18–20], решаемое методом сферических гармоник [19–23]. Схема программы расчёта подробно описана в [15]. Для расчёта экспериментально измеряемых величин из полученных коэффициентов при полиномах Лежандра на границах слоя использовались выражения, учитывающие измерение коэффициента пропускания относительно кюветы сравнения:

N

P d = Z ( - 1 ) m C m ( 0 ) ^ m , m = 0

N

T d = Z Cm ( d К m ,                            (1)

m = 0

T t =T d+ exp(-^ td), где d – толщина слоя образца, Cm(0) и Cm – коэффициенты разложения освещённости по полиномам Лежандра на передней и задней границах образца соот- ветственно, ρd, τd и τt – коэффициенты диффузного отражения, пропускания и полного пропускания (сумма коэффициентов диффузного и коллимированного пропускания) соответственно, µt – показатель ослабления, равный сумме показателей рассеяния µs и поглощения µa света. Коэффициенты, учитывающие вклад каждой гармоники на границах в величины коэффициентов диффузного отражения и пропускания, имеют вид [14, 15]:

• 5    m = m1 J Pm (O)-[1 - R (Q)]-Q dQ , (2) 20

2.    Методика и результаты эксперимента

где P m (Ω) – полином Лежандра, Ω – косинус угла, отсчитываемого от нормали, совпадающей с направлением падающего излучения, m – номер гармоники, R (Ω) – френелевская зависимость энергетического коэффициента отражения света от границы образца. При расчёте R (Ω) для прессованных таблеток использовался показатель преломления матрицы [15]. В случае кюветы, заполненной суспензией, появляются две границы: растворитель – кюветная стенка и кюветная стенка – воздух.

Рассмотрим предельный случай тонкого слоя образца в кювете с толстой стенкой. Будем считать, что поперечные размеры кюветы также превышают размеры окна интегрирующей сферы, используемой для измерений. Диффузно рассеянный свет попадает из образца в кюветную стенку под различными углами, которые могут превышать угол полного внутреннего отражения на границе кюветная стенка – воздух. В этом случае свет будет отражаться обратно в сторону суспензии. Если толщина стенки достаточно велика, свет попадёт обратно в суспензию в удаленной точке, из которой его возвращение в область окна сферы маловероятно. Поэтому в пределе кюветы с толстой стенкой под R (Ω) должен пониматься коэффициент отражения на границе стекло – воздух, а не суспензия – стекло.

Для определения спектральных зависимостей коэффициентов диффузного отражения, пропускания и полного пропускания (сумма коллимированной и диффузной компонент) образцов в диапазоне 400– 800 нм использовался двухлучевой спектрофотометр Shimadzu UV-2450, оснащённый интегрирующей сферой. При измерении коэффициента диффузного пропускания выходное окно интегрирующей сферы оставалось открытым, пропуская коллимированный пучок, прошедший через образец [24]. Измерения проводились в стеклянных кюветах стандарта КФК с толщиной слоя вещества L =0,1 см и толщиной стенок lw =0,3 см. Ширина и высота кюветы (2,4×3,3 см2) превышали соответствующие размеры окна интегрирующей сферы (1,0×1,5 см2). В качестве стандарта белого тела применялся слабо прессованный порошок сульфата бария. Определение коэффициента пропускания осуществлялось относительно кюветы сравнения с чистым растворите- лем. В качестве модельного образца выступала суспензия диоксида титана TiO2 (сферические частицы с характерными размерами 90 нм. Приобретён у компании Plasmotherm) в смеси этилового спирта и глицерина (в объемном соотношении 1:1), содержащая краситель метиленовый красный. Для гомогенизации суспензия перед измерениями перемешивалась в ультразвуковой ванне не менее 10 минут. Показатель преломления растворителя, измеренный на дифрактометре, составил 1,42.

Измеренные спектральные зависимости коэффициентов диффузного отражения ρ _d и пропускания τ _d и полного пропускания τ _t для образца с концентрациями метиленового красного и диоксида титана 0,05 мг/мл и 1,35 мг/мл соответственно приведены на рис. 1.

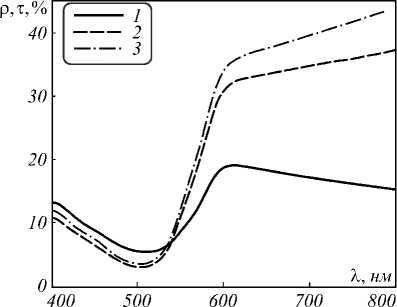
Рис. 1. Экспериментальные спектральные зависимости коэффициентов диффузного отражения (1), диффузного пропускания (2) и полного пропускания (3) модельной суспензии диоксида титана, содержащей метиленовый красный

В области длин волн от 800 до 615 нм по мере уменьшения длины волны наблюдается увеличение коэффициента диффузного отражения (кривая 1 рис. 1) с одновременным уменьшением коэффициентов диффузного (кривая 2 рис. 1) и полного (кривая 3 рис. 1) пропускания. При длине волны 612 нм на зависимости ρ _d (λ) наблюдается максимум с амплитудой 19,1 %. Далее в области от 615 до ~500 нм происходит симбатное уменьшение коэффициентов диффузного пропускания и отражения. Данные величины достигают минимума при значениях длины волны 503 и 511 нм соответственно, значения τ d и ρ d в данных точках составляют 3,1 и 5,5 %. При дальнейшем уменьшении длины волны происходит небольшое увеличение обеих величин τ _d и ρ _d .

Наблюдаемые изменения коэффициентов диффузного пропускания и отражения по мере уменьшения длины волны определяются спектральными зависимостями показателей поглощения и рассеяния образцов. В области λ >620 нм краситель метиленовый красный не поглощает электромагнитное излучение. В результате зависимости τ d (λ) и ρ d (λ) антибатны. Рассмотрим в этой области спектра функцию, показывающую отношение суммарной интенсивности диффузно отражённого и пропущенного света к ослаблению интенсивности исходного пучка:

F ( % ) =

t d C^)+p d (%) 100— tt (%) + td (%)’

где величины коэффициентов пропускания и отражения приведены в процентах. Во всей исследованной области длин волны значение F составляет 0,55 с абсолютным изменением не более чем на 0,03. Отметим, что F < 1, то есть значительная доля диффузно рассеянного излучения выходит из кюветы вне области окна сферы.

Используя величину оптической плотности, вычисляемой как –lg(τ _t – τ _d ), была получена спектральная зависимость показателя рассеяния (см^–1) в области 620–800 нм. Для аппроксимации, как и в [25–31], использовалась степенная функция ц _s ( % )= 10052 -Х ^-0,8862.

3.    Моделирование спектральных зависимостей

Аппроксимация спектральных зависимостей коэффициентов диффузного пропускания и отражения в области прозрачности красителя 620–800 нм выполнялась с использованием в выражении (2) угловой зависимости для энергетического коэффициента отражения при относительных показателях преломления для границ стекло – воздух и растворитель – стекло. Коэффициенты разложения при гармониках определялись из граничных условий на поверхности кюветная стенка – суспензия. При моделировании использовались значения показателя рассеяния, определённые по разности коэффициентов диффузного и полного пропускания, альбедо однократного рассеяния принималось равным 1. Для оптимального описания использовался метод Нейлдера–Мида с вариацией фактора анизотропии рассеяния, задаваемого в виде линейной функции длины волны. Индикатриса рассеяния вычислялась по формуле Хеньи–Гринстей-на [32] с линейно зависящим от длины волны фактором анизотропии.

На рис. 2 показаны результаты аппроксимации спектральных зависимостей коэффициентов диффузного отражения (кривая 1 на рис. 2) и пропускания (кривая 2 на рис. 2) в области 640–800 нм в рамках модели переноса излучения при альбедо равном 1 при использовании угловых зависимостей коэффициента отражения для границ стекло – воздух (кривые 3 и 4 на рис. 2) и растворитель – стекло (кривые 5 и 6 на рис. 2). Из полученных данных следует, что удовлетворительное описание достигается только в первом случае при факторе анизотропии, определяемом выражением 0,608+1,943- 10—4.(Х-800). Об этом же свидетельствуют величины суммы квадратов отклонений, нормированной на число точек: 0,13 и 502%2 соответственно. Для расчёта спектральных зависимостей коэффициентов диффузного отражения и пропускания в области поглощения красителя использовался эталонный спектр молярного коэффициента поглощения и введённая концентрация метиленового красного. Величина показателя рассеяния экстраполировалась из области 640–800 нм, в которой поглощение света отсутствует. Величина фактора анизотропии определялась линейным выражением, коэффициенты в котором были получены при оптимальном описании спектральных зависимостей коэффициентов диффузного отражения и пропускания в области прозрачности красителя. Результаты расчётов и их сравнение с экспериментом представлены на рис. 3.

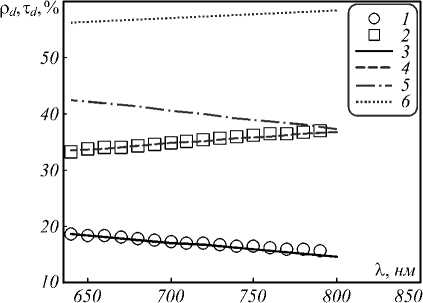
Рис. 2. Экспериментальные (1, 2) и рассчитанные (3–6) зависимости коэффициентов диффузного отражения (1, 3, 5) и пропускания (2, 4, 6) от длины волны при учете отражения от внешней стенки кюветы (3, 4) и без него (5, 6) в области прозрачности красителя

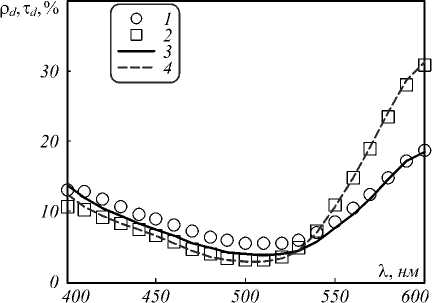
Рис. 3. Экспериментальные (1, 2) и рассчитанные (3, 4) зависимости коэффициентов диффузного отражения (1, 3) и пропускания (2, 4) от длины волны в области полосы поглощения метиленового красного

Из сравнения видно хорошее соответствие для зависимости τ _d (λ) (кривая 4 на рис. 3), для зависимости ρ _d (λ) (кривая 3 на рис. 3) согласие с экспериментом (кривые 1 и 2 на рис. 3 соответственно) несколько хуже. Наиболее высокие расхождения наблюдаются в области длин волн менее 540 нм, хотя абсциссы минимумов на экспериментальной и рассчитанной кривых совпадают. Сумма квадратов отклонений, нормированная на число точек, составила 0,65 %². Данную величину можно рассматривать как свидетельство хорошего согласия с экспериментом, учитывая то, что все дополнительные параметры были определены в области прозрачности красителя.

4.    Обсуждение результатов

Экспериментальные результаты свидетельствуют о необычной и недостаточно исследованной особенности измеренных спектров диффузного отражения и пропускания суспензий, связанной с неполным попаданием диффузно рассеянного света в интегрирую- щую сферу спектрофотометра. Наиболее отчётливо эффект проявляется при рассмотренной в работе геометрии измерения, когда значения функции F меньше единицы во всей исследованной области спектра, включая область прозрачности красителя. Для использованной схемы измерения (окно сферы меньше поперечных размеров кюветы) можно выделить две основные причины наблюдаемого эффекта:

• 1.    Расширение области взаимодействия света с веществом за счёт его рассеяния.

• 2.    Отражение света от передней и задней стенок кюветы в область образца, из которой его попадание в окно сферы становится маловероятным.

Первый эффект может привести к существенным искажениям результатов, если обратная величина показателя ослабления сопоставима с размерами окна интегрирующей сферы. В нашем случае данная величина максимальна при длине волны 800 нм, составляя 0,037 см, что значительно меньше ширины окна. Поэтому данный эффект оказывает менее сильное влияние на результаты, хотя его вклад может возрасти при использовании кювет с большей толщиной слоя образца. Кюветная стенка, на первый взгляд, не должна влиять на результаты измерений, поскольку попавший в кювету квант света при альбедо, равном единице, должен её покинуть после ряда актов рассеяния. В то же время совсем не обязательно, что после этого он попадёт в окно сферы и будет зафиксирован. Предложенная схема расчёта даёт упрощенную оценку доли прошедшего света, считая, что попадание в окно сферы первично отражённого света под углами большими, чем угол полного внутреннего отражения, пренебрежимо мало. Чем больше толщина стенки, тем с большей точностью будет выполняться данное приближение. В нашем случае толщина стенки составляла 0,3 см, угол полного внутреннего отражения – 0,253π, соответственно, свет, идущий от границы раздела суспензия – стекло под данным углом, вернётся после отражения от поверхности стекло – воздух, пройдя 0,61 см, что сопоставимо с шириной окна сферы. Поэтому данное приближение применимо для условий измерения спектральных зависимостей.

В настоящей работе выбрана схема учёта кюветной стенки, заключающаяся в расчёте распределения освещённости только внутри суспензии и корректировки вкладов гармоник в диффузное отражение и пропускание с учётом отражения от границы стекло кюветы – воздух. Если не учитывать последнее обстоятельство, в спектральной области прозрачности красителя значительно большая доля диффузно рассеянного излучения будет покидать образец. В результате величина F будет близка к единице (сравните с кривыми 5 и 6 на рис. 2), что непосредственно противоречит эксперименту.

Результаты моделирования на рис. 3 неплохо согласуются с экспериментальными данными. Некоторые количественные отклонения могут определяться следующими причинами. Диоксид титана имеет по- верхностные кислотные и щелочные центры, наличие которых может привести к искажению спектра красителя метиленового красного. Данным эффектом мы пренебрегали в настоящей работе, хотя он должен проявляться при возникновении равновесия адсорбции-десорбции красителя [33] и приводить к увеличению коэффициента диффузного отражения. В силу отмеченных обстоятельств, следует признать удовлетворительным согласие данных расчёта и эксперимента (рис. 3).

Исследованные в настоящей работы эффекты могут возникать в большом количестве приложений, включающих исследование оптических свойств тканей растительных [3, 4] и животных организмов in vitro [6–9, 11]. Как следует из полученных результатов, их учёт является принципиально важным, особенно при решении обратных задач построения спектральных зависимостей показателей поглощения и рассеяния на основе данных эксперимента.

Заключение

Предложен приближённый способ учёта кюветной стенки при расчёте коэффициентов диффузного отражения и пропускания в рамках одномерного уравнения переноса излучения в предельном случае тонкого слоя образца и широкой кюветной стенки. Рассмотрена схема расчёта, в которой вначале в области прозрачности красителя определяется фактор анизотропии индикатрисы рассеяния, затем моделируется спектр коэффициентов диффузного отражения и пропускания в области полосы поглощения. Верификация метода выполнена на примере модельной суспензии диоксида титана, содержащей краситель метиленовый красный. Показано, что учёт кюветной стенки позволяет объяснить неполное попадание рассеянного излучения в интегрирующую сферу.

Работа выполнена при поддержке РФФИ (№ 1403-00534 А), гранта президента РФ (МК-4331.2015.2) и Министерства образования и науки РФ (НИР № 3603 по заданию № 2014/64).