Особенности оценки радиационной стойкости космической микро- и наноэлектроники

Простые оценки показывают, что в треке одиночного тяжелого иона перед остановкой формируется локальная доза энергии более 107 рад. При этом объемная плотность мощности при остановке иона кремния в кремнии в области пика Брэгга составляет 1012 Вт/см3. Для сравнения, объемная плотность мощности при взрыве динамита 5·108 Вт/см3, объемная плотность мощности теплового процесса ядерного взрыва — 1014 Вт/см3. Релаксация такого возбуждения может приводить к необычным структурным, фазовым и химическим превращениям облучаемого вещества в ближней окрестности траектории иона.

Результаты исследований в этом направлении [1] позволяют уже в настоящее время прийти к пониманию ряда практических вопросов, связанных с определением сроков активного функционирования микро- и наноэлектроники в поле ионизирующих частиц (ИЧ), создаваемом космическими лучами в космических аппаратах (КА).

Настоящая работа обращает внимание на тот факт, что частота одиночных событий нештатной работы микроэлектронных элементов во время эксплуатации на КА существенно меньше, чем ее оценка при наземной отработке на существующих моделирующих стендах. Как следствие, применяемые методы испытаний и оценок стойкости электроники в полях ионизирующих излучений (ИИ) в настоящее время приводят зачастую к ложноотрицательным заключениям о применимости электронных комплектующих в космических приборах. Основная причина ошибочной оценки радиационной стойкости по ныне действующим методикам заключается в процедуре использования макро-дозиметрического критериального параметра — «полная доза».

Параметр «доза» в свое время был введен для применения в дозиметрии при оценке воздействия ядерного взрыва. В связи с тем, что размеры чувствительных объемов микроэлектроники теперь сопоставимы с диаметром трека ИЧ, становится целесообразным использовать нанодозиметрические критерии оценки поля ИЧ.

Сопоставление микродозиметрических характеристик поля ИЧ на КА с соответствующими параметрами ряда изотопных источников показывает, что характерные плотности энерговыделения в реальных чувствительных объемах могут быть воспроизведены на относительно несложных и недорогих испытательных стендах на базе изотопных источников. Такой подход позволит сократить вероятность выхода ложноотрицательных заключений, и, соответственно, существенно расширить перечень применяемых комплектующих.

недостатки традиционного подхода

Традиционно степень воздействия ИИ на среду описывают поглощенной дозой — количеством поглощенной некоторым объемом среды энергии излучения, отнесенным к массе вещества в этом объеме. Описание это является макроскопическим, пока геометрические размеры рассматриваемого объема существенно превосходят размеры треков частиц, оставивших в нем энергию. Макроскопический дозовый подход сложился десятилетия назад, когда сомнений в его применимости к аппаратуре не возникало в силу характерных для того времени размеров функциональных элементов электронных приборов (ЭП). Современный уровень интеграции полупроводниковых приборов дает все основания для таких сомнений.

Распределение поглощенной энергии внутри объема облучаемой среды зависит от масштабов рассмотрения. При обычном макроскопическом рассмотрении производится усреднение воздействия излучения по всему объему и по значительному временному интервалу. В этом случае детали распределения полностью теряются, воздействие излучения характеризуется только одним числом — дозой за временной интервал. Другая крайность — рассмотрение в геометрических и временных масштабах, соответствующих треку одной ИЧ. При этом оказывается, что распределение поглощенной энергии (плотности поглощенной энергии, плотности дозы и т. п.) как вдоль, так и поперек трека оказывается вовсе не однородным.

основы альтернативного подхода

Рассмотрим современное представление о геометрических и временных масштабах воздействия космического излучения на вещество. Для определенности будем говорить о заряженных частицах с энергиями 1 кэВ…1 ГэВ, поскольку их много в космическом пространстве и они эффективно теряют энергию на ионизацию среды. К тому же, гамма-кванты и нейтроны воздействуют на среду в основном через вторичные заряженные частицы, являющиеся результатом взаимодействий нейтралов. Ультрарелятивистская (т. е. имеющая скорость, практически совпадающую со скоростью света в вакууме) частица пролетает почти 300 мм за 1 нс, 300 мкм — за 1 пс и 300 нм — за 1 фс. Для нерелятивистской частицы скорость v связана с кинетической энергией T простым соотношением v = c i 2 T / m , где m — масса покоя частицы.

Для протона с кинетической энергией 5 МэВ получаем v = 0,1 c ( c — скорость света), т. е. он проходит 300 нм за 10 фс. Это означает, что собственно процесс прохождения частицы через полупроводниковый прибор толщиной ~100 мкм происходит за десятки пикосекунд. Результатом пролета частицы является делокализация и нагрев электронов среды в окрестности траектории с последующим нагревом решетки материала [2, 3]. За время порядка нескольких пикосекунд происходит формирование трека частицы — области радиусом в несколько нанометров, в которой установлено тепловое равновесие как системы делокализованных электронов, так и решетки.

В зависимости от плотности выделенной энергии возможны различные последствия прохождения частицы через вещество — от временных изменений проводимости до перестройки структуры решетки. Плотность энерговыделения флуктуирует вдоль трека отдельной частицы-снаряда, причем чем меньше масштаб усреднения плотности, тем больше флуктуации, т. е. тем шире спектр плотностей линейного поглощения энергии.

На рис. 1 приведены результаты моделирования распространения альфа-частиц с начальной кинетической энергией 1 МэВ в кремнии. Для расчетов был использован пакет GEANT4.10.01 [4]. Всего было смоделировано 10 000 траекторий. Частицы-снаряды начинали движение в центре кремниевого куба размером 10×10×10 мкм и двигались до остановки. Траектория каждой частицы прослеживалась в трех координатах с геометрическим шагом 1 нм, энерговыделение на каждом шаге записывалось. Энерговыделению присваивались координаты конечной точки шага. В дальнейшем энерговыделения были спроецированы на направление первоначального движения частицы-снаряда (ось Z) и просуммированы на сетках с тремя различными шагами — 10, 100 и 1 000 нм. Затем энерговыделение в каждом бине каждой сетки для каждой частицы делилось на ширину бина сетки (шага сетки), что давало линейную плотность энерговыделения с соответствующим масштабом усреднения. На рис. 1, а, б, в приведены спектры линейных плотностей энерговыделений для шагов 10, 100 и 1 000 нм, соответственно. На рис. 1, г показаны усредненные по всем траекториям зависимости линейной плотности энерговыделений от Z для разных масштабов усреднения, полученные следующим образом: энерговыделения были просуммированы на каждой из трех сеток по всем траекториям и затем поделены на длину шага сетки. Такой способ получения средних зависимостей линейной плотности энерговыделений от Z приближает их к кривым линейной передачи энергии (ЛПЭ).

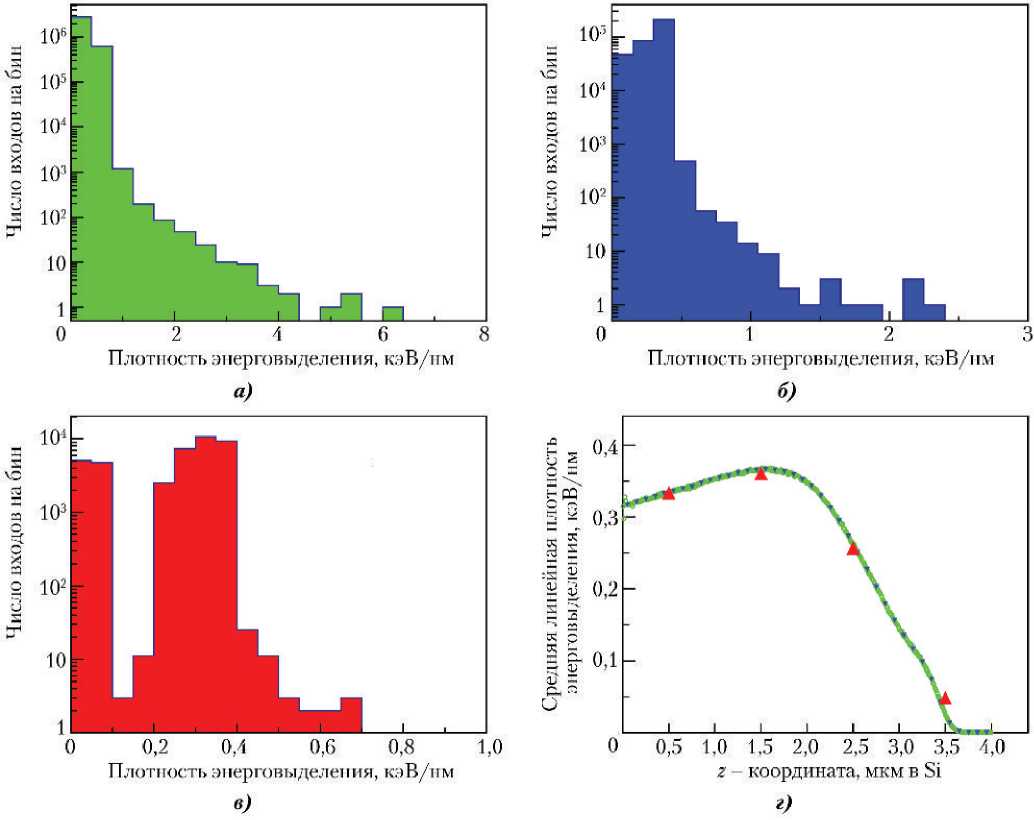
Рис. 1. Результаты моделирования распространения альфа-частиц с энергией 1 МэВ в кремнии: а — спектр плотностей энерговыделений (СПЭ) с масштабом усреднения 10 нм, среднее значение плотности 0,292 кэВ/нм, среднеквадратичное отклонение 0,125 кэВ/нм; б — СПЭ с масштабом усреднения 100 нм, среднее значение плотности 0,289 кэВ/нм, среднеквадратичное отклонение 0,097 кэВ/нм; в — СПЭ с масштабом усреднения 1 000 нм, среднее значение плотности 0,251 кэВ/нм, среднеквадратичное отклонение 0,122 кэВ/нм; г — зависимости линейной передачи энергии от Z-координаты для разных масштабов усреднения: — 10 нм, ▼ — 100 нм, ▲ — 1 000 нм

Рис. 1, а, б, в подтверждает сделанное выше утверждение о расширении спектра плотностей энерговыделений (СПЭ) с уменьшением масштаба усреднения: если при шаге сетки 1 000 нм максимальная плотность энерговыделений (правая граница спектра) достигает примерно 0,7 кэВ/нм, то при шаге 100 нм она уже превышает 2 кэВ/нм, а при шаге 10 нм составляет примерно 6 кэВ/нм. При этом средняя линейная плотность энерговыделений (ЛПЭ, рис. 1, г ) с хорошей точностью не зависит от масштаба усреднения.

Иными словами, ЛПЭ как средняя характеристика не содержит информации о флуктуациях, а именно — большие флуктуации плотности энерговыделений представляют опасность для ЭП с высокой степенью интеграции (т. е. с малыми размерами функциональных элементов).

Сказанное выше означает, что даже после прохождения одной заряженной частицы малый функциональный элемент прибора размером порядка десятков нанометров может получить большую поглощенную дозу, способную повлиять на его работу. Таким образом, макроскопическое рассмотрение, т. е. рассмотрение с масштабом усреднения, значительно превышающим характерный размер функционального элемента прибора, может привести к неправильному заключению относительно радиационной безопасности прибора. Если ориентироваться на макроскопическую дозу и даже на ЛПЭ, размеры флуктуаций не видны, что неминуемо приводит к недооценке опасности. Попытка скомпенсировать незнание флуктуаций (высоких локальных мгновенных доз) введением некоторого постоянного коэффициента, имеющего смысл запаса прочности, может привести к переоценке радиационной опасности (РО), поскольку такой коэффициент должен зависеть от расположения рассматриваемого прибора в КА, характеристик источника ИИ, режима работы прибора и т. п.

Следовательно, для получения корректной оценки РО требуется статистический подход, основанный на статистическом моделировании прохождения излучения через конструкции КА. В радиационной терапии расчеты радиационного воздействия по Монте-Карло используются уже давно и дают хорошие результаты. В случае оценки радиационной безопасности космической электроники проблема имеет характерные особенности:

• •    источники излучения могут непредсказуемо менять характеристики во времени и пространстве, и измерение этих характеристик представляет проблему;

• •    чувствительные элементы аппаратуры имеют малые (нано) масштабы;

• •    для оценки вероятности тех или иных повреждений конкретных ЭП в различных радиационных условиях нужно иметь возможность воспроизвести эти радиационные условия в лаборатории.

Рассмотрим последовательно пути решения этих проблем.

как сравнивать источники ионизирующих излучений с точки зрения радиационных воздействий на электронные приборы?

Ответ на этот вопрос прост и естественен: поскольку, как мы выяснили, нас прежде всего интересуют СПЭ, именно по этим характеристикам имеет смысл сопоставлять внешние источники, создающие радиационные поля внутри КА. Энергетические спектры и состав излучений вне КА, являясь причиной СПЭ, не важны для нас с точки зрения радиационной безопасности ЭП, если мы знаем СПЭ внутри этих приборов. Таким образом, остается понять, как получить СПЭ, причем с характерными масштабами усреднения.

как оценивать радиационные воздействия в наномасштабах?

Обычные детекторы ИИ с точки зрения обсуждаемых проблем имеют макромасштабы. Однако, существуют и широко используются такие полупроводниковые приборы, как ПЗС- и КМОП-матрицы, по существу представляющие собой двумерные наборы полупроводниковых детекторов микрометрических размеров. Они уже широко используются как трековые/вершинные детекторы в физике высоких энергий и космической физике. Мы уже использовали их для оценки СПЭ как в лабораторных условиях, так и в спутниковых экспериментах [5]. Осталось перевести СПЭ, непосредственно измеренный в микромасштабах, в СПЭ в наномасштабах. Такое преобразование должно опираться на результаты статистического моделирования. Пример такого расчета был приведен на рис. 1, а, б, в .

Существующие ПЗС-матрицы в основном создаются как фотосенсоры, что определяет микронные размеры их ячеек. Естественно предположить, что потребности мониторинга РО приведут к разработке специальных матриц новых типов с меньшими размерами ячеек, с различными формами и размерами чувствительных областей, с удобным для радиационного мониторинга электронным интерфейсом.

Нельзя не упомянуть и о более дешевой альтернативе специальным матрицам: в принципе, в качестве сенсора можно использовать хорошо изученную микросхему подходящей степени интеграции, установленную вблизи охраняемого ЭП. Правда, отклик такого сенсора на радиационное воздействие, скорее всего, будет более сложным, чем показания стандартной матрицы, что ставит под сомнение выгоду от его использования.

как отслеживать характеристики ионизирующих излучений in situ?

Ответ на этот вопрос фактически уже был дан выше: сенсор СПЭ следует размещать вблизи электронных компонентов, радиационная безопасность которых контролируется. Термин «вблизи» должен быть определен для конкретных компоновки и состава аппаратуры, поскольку это влияет на распространение излучения. В любом случае, задача мониторинга требует статистического моделирования прохождения излучения через КА.

можно ли воспроизвести космические радиационные поля в лаборатории?

Сертификация ЭП на радиационную стойкость в традиционном дозовом подходе в настоящее время производится на ускорителях заряженных частиц и рентгеновских установках по методикам, недоступным создателям аппаратуры. Это делает процесс сертификации закрытым, субъективным и дорогим. В случае использования микроскопического подхода, точнее, подхода СПЭ, такая отстраненность разработчика и пользователя аппаратуры от процесса изучения ее радиационной стойкости оказывается крайне нежелательной, если вообще возможной. Четверть века назад введен и ныне действует документ отрасли РД 50-25645.217-90 [7]. Он регламентирует методики расчета ми-кродозиметрических характеристик космических излучений для обеспечения радиационной безопасности экипажа КА. За это время существенно уточнились теоретические представления о процессах в треке и физике релаксации экстремального состояния вещества в керне трека. Настала насущная необходимость разработки аналогичного документа для обеспечения стойкости космической наноэлектроники.

Имеется возможность удешевить и приблизить к разработчику как процесс традиционной сертификации ЭП на радиационную стойкость, так и более индивидуальный процесс изучения их отклика в рамках подхода СПЭ. Возможность эта связана с использованием компактных источников нейтронов на паре Pu–Be. Pu–Be-источники используют альфа-частицы от распада плутония, которые в результате ядерной реакции (α, n ) на бериллии производят нейтроны, имеющие сплошной спектр кинетических энергий от 0,1 до 12 МэВ с максимумом в районе 3–5 МэВ. Нейтроны таких энергий обладают большой проникающей способностью и испытывают, в основном, упругие взаимодействия, результатом которых являются ядра отдачи — ядра среды, выбитые из своего законного места в кристаллической решетке и получившие кинетическую энергию, достаточную для ионизации среды. На рис. 2, а, б показаны спектры кинетических энергий ядер отдачи, производимые пучком нейтронов с кинетическими энергиями 5 и 10 МэВ, соответственно.

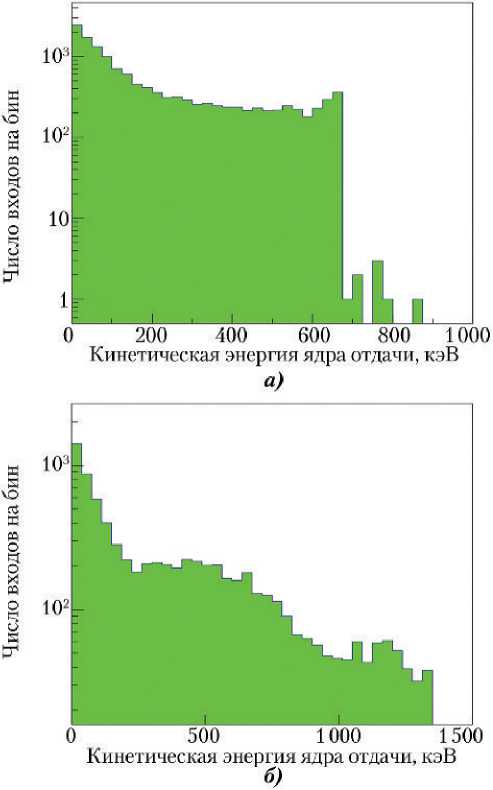
Рис. 2. Энергетические спектры ядер 28Si, 29Si и 30Si, выбитых из решетки кристалла кремния нейтронами с кинетическими энергиями 5 МэВ (а) и 10 МэВ (б)

Посмотрим теперь на СПЭ, создаваемые в кремнии этими ядрами отдачи. Для энергии 600 кэВ, представленной в обоих спектрах на рис. 2, а, б, получаем набор СПЭ и кривую ЛПЭ, показанные на рис. 3. Форма спектра с масштабом усреднения 1 000 нм (рис. 3, в) отличается от аналогичного спектра на рис. 1, в формой, средним значением, вариацией, но не диапазоном плотностей энерговыделений. Спектры с масштабами усреднения 10 и 100 нм (рис. 3, а, б) похожи по форме на спектры рис. 1, а, б, но имеют существенно более длинные хвосты, что гарантирует нам получение высоких плотностей энерговыделений, вплоть до ~20 и ~6 кэВ/нм, соответственно. Таких плотностей не было в СПЭ альфа-частиц, но они могут встретиться в спектрах более тяжелых ионов.

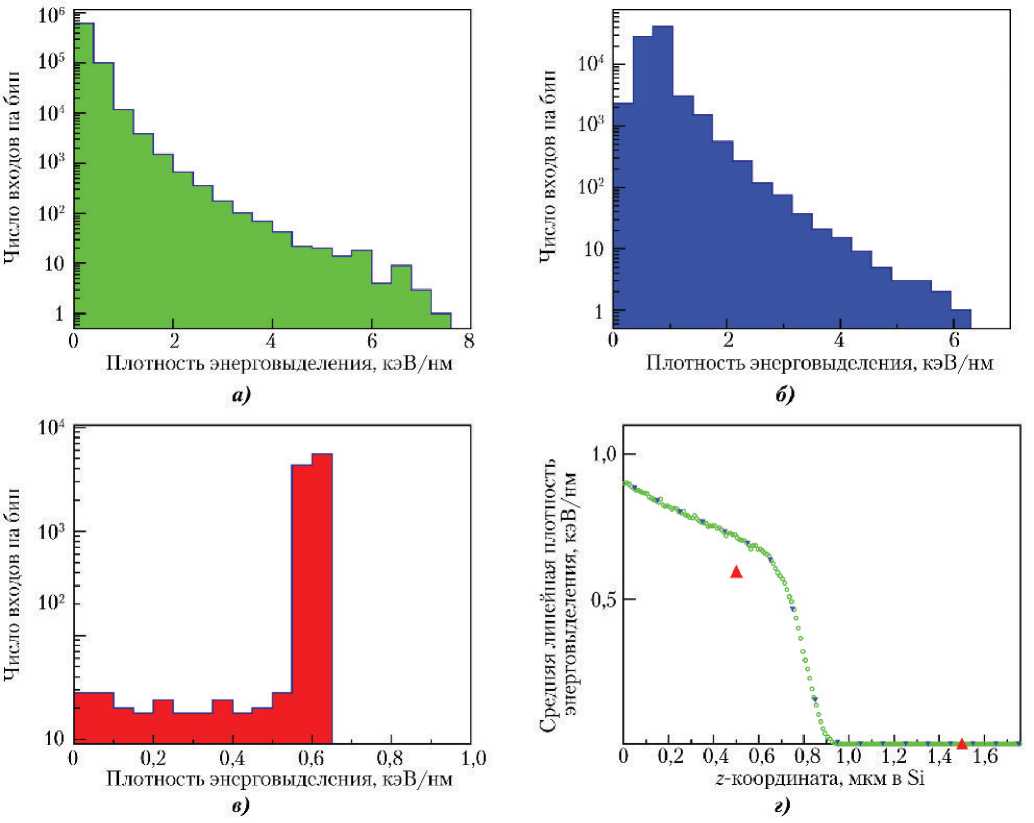
Рис. 3. Результаты моделирования распространения ядер кремния с энергией 0,6 МэВ в кремнии: СПЭ с масштабами усреднения 10 нм (а), 100 нм (б) и 1000 нм (в); г — зависимости линейной передачи энергии от Z-координаты для разных масштабов усреднения (обозначения такие же, как на рис. 1, г)

В спектре на рис. 2, б представлены и ядра отдачи больших энергий, способные создать еще большие плотности энерговыделений. Это подтверждает рис. 4, дающий СПЭ для тех же трех масштабов усреднения и кривую ЛПЭ для ионов кремния с кинетической энергией 1,2 МэВ. В этом случае СПЭ имеют еще большие диапазоны плотностей энерговыделений, что демонстрирует серьезный потенциал Pu–Be-источников с точки зрения воспроизведения СПЭ, возникающих в действующей космической аппаратуре.

Почему мы подчеркиваем именно возможности создания высоких плотностей энерговыделений в лабораторных условиях с помощью Pu–Be-источников? В рамках изложенных выше представлений о процессе формирования трека естественно предположить, что именно возникновение больших плотностей энерговыделений является причиной одиночных событий в ЭП высокой степени интеграции. Сечения одиночных событий обычно представляют в зависимости от остаточного заряда (т. е. от количества электронно-дырочных пар, остающихся по окончании формирования трека и доступных для непосредственного измерения), причем зависимость эта носит пороговый характер: сечение резко нарастает при превышении остаточным зарядом некоторого критического значения («критического заряда»), характерного для данной технологии производства и/или данного типа ЭП. Остаточный заряд сильно коррелирован с плотностью энерговыделения, что позволяет говорить о критической плотности энерговыделения наряду с критическим зарядом.

Таким образом, возможность изучать в лаборатории реакцию электронных приборов на поток излучения контролируемого качества трудно переоценить. Для контроля спектра плотностей энерговыделений в лабораторных условиях имеет смысл использовать те же сенсоры (ПЗС-матрицы, специальные матрицы и т. п.), что и в космических условиях. Это позволяет сравнивать космические и лабораторные радиационные воздействия и воспроизводить в лаборатории происходящее в космосе.

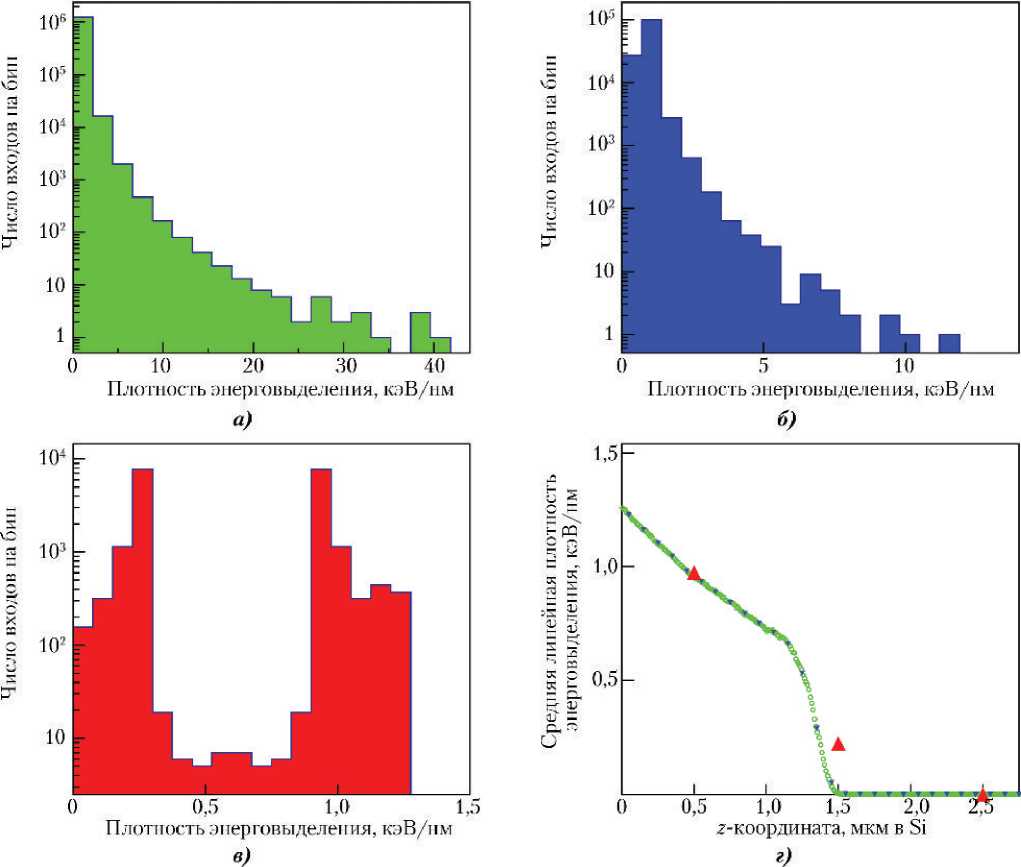
Рис. 4. Результаты моделирования распространения ядер кремния с энергией 1,2 МэВ в кремнии: СПЭ с масштабами усреднения 10 нм (а), 100 нм (б) и 1 000 нм (в); г — зависимости линейной передачи энергии от Z-координаты для разных масштабов усреднения (обозначения такие же, как на рис. 1, г)

Проблема воспроизведения СПЭ с помощью компактных нейтронных источников не столь проста, как может показаться из сказанного выше. Она включает технологические и вычислительные аспекты, причем для статистического моделирования требуются значительные вычислительные мощности и специальное матобеспечение. Вместе с тем, предлагаемый подход обладает значительной гибкостью и позволяет разработчикам и пользователям участвовать в обеспечении радиационной стойкости соз-даваемой/используемой аппаратуры, не требуя значительных материальных затрат.

Отменяет ли предлагаемый подход СПЭ традиционный дозовый макроподход? Нет, соотношения двух подходов более сложные. Традиционный подход остается актуальным для многих приложений, предполагающих высокие интенсивности излучений и использование массивных ЭП, не подверженных тонким локальным эффектам. Предлагаемый подход объективно лучше соответствует проблеме радиационной защиты ЭП в космических условиях. Компактные источники нейтронов можно использовать и для дозовых тестов, хотя скорость набора дозы неминуемо будет меньше, чем в ускорительных пучках, из-за относительно небольшой интенсивности потока нейтронов. Важно и то, что эти источники дают существенный поток рентгеновского и гамма-излучения (большой диапазон коэффициента качества при испытании на полную дозу). Идеологию СПЭ лучше всего использовать в комплексе: сенсоры СПЭ (например, ПЗС-матрицы), установленные на функционирующих бортах, позволят осуществлять глобальный мониторинг РО. Эту информацию можно использовать как оперативно — для предотвращения выхода из строя ценной аппаратуры на основании ранее проведенных лабораторных измерений и расчетов, так и при разработке новой аппаратуры.

Переход к работе в парадигме СПЭ означает изменение роли и ответственности разработчиков и пользователей электронной аппаратуры, поскольку реальный эффект от применения более адекватных физических моделей может быть получен только при сознательном использовании новых возможностей. Требуется также перестройка нормативной базы, чтобы разработчики имели права выполнять те функции, которые в настоящее время им недоступны.

заключение

• 1.    Корректный расчет СПЭ возможен только в рамках полного статистического (Монте-Карло) моделирования прохождения излучения через конструкции рассматриваемой аппаратуры (или ткани живого организма). При этом возможно получение СПЭ на геометрических масштабах функциональных элементов приборов.

• 2.    Измерение спектров плотностей на масштабах функциональных элементов может оказаться невозможным для наномасштабов. Однако, использование ПЗС-матриц с микронными размерами пикселов обеспечивает измерение спектров на этих масштабах, а переход к спектрам на наномасштабах от спектров на микромасштабах может быть

• 3.    СПЭ непосредственно связан с вероятностями одиночных событий в ЭП.

• 4.    Оценку радиационной стойкости ЭП можно проводить в наземных условиях с помощью Pu–Be нейтронного источника. Воспроизведение существующего в космическом пространстве СПЭ в лабораторных условиях можно контролировать с помощью ПЗС-монитора: СПЭ в ПЗС-матрице в космосе и лаборатории должны быть близки.

• 5.    Микроскопическое рассмотрение радиационной стойкости, таким образом, требует комплексного подхода: мониторинг in situ + лабораторный эксперимент + расчет.

• 6.    Расчеты плотностей энерговыделений или мощностей энерговыделений в конкретных ЭП, размещенных в заданных точках КА, могут потребовать обширных вычислительных ресурсов.

произведен расчетным путем и, отчасти, экстраполяцией.