Особенности острой фокусировки вихревых пучков Гаусса-Лагерра

Известно, что фазовая сингулярность может быть использована для усиления продольной компоненты электрического вектора лазерного излучения [1 –8] в случае однородной (линейной и круговой) поляризации, которую производят большинство современных лазеров. В частности, в работах [1, 2, 5, 7, 8] рассматривались вихревые фазовые функции, а в работах [3, 4, 6] – суперпозиции вихревых фазовых функций как соосных [3, 4], так и пространственно разделённых [6].

Наличие мощной продольной компоненты в области фокуса позволяет улучшить оптическое разрешение и используется для оптического манипулирования, ускорения электронов, обработки материалов, в микроскопии и других приложениях [9– 14].

Заметим, что энергия продольной компоненты становится существенной только при высоких значениях числовой апертурой (NA>0,7). Снизить это требование можно за счёт использования лазерных пучков высокого порядка [15, 16]. При этом, как правило, рассматриваются пучки с более высоким радиальным индексом. Однако особенности, связанные с фокусировкой вихревых пучков с высокими угловыми индексами, также представляют интерес, особенно в задачах оптического манипулирования [17], основанных на передаче углового момента [18, 19].

Таким образом, в данной работе рассматриваются особенности острой фокусировки вихревых лазерных пучков Гаусса–Лагерра (ГЛ) для различных типов однородной поляризации в зависимости от порядка вихревой фазы.

1.    Острая фокусировка мод Гаусса–Лагерра

Рассмотрим высокоапертурную апланатическую фокусирующую оптическую систему, фокус которой расположен на расстоянии значительно большем, чем длина волны от апертуры. Тогда вектор электрического поля в однородной диэлектрической среде вблизи фокуса может быть описан с помощью приближении Дебая:

α 2 π

E ( ρ , ϕ , z ) =-        B ( θ , φ ) T ( θ ) P ( θ , φ ) ×

λ 0 0                                      (1)

×exp[ik (ρ sin θ cos(φ - ϕ) + zcos θ)] sin θdθdφ, где (ρ, ϕ, z) – цилиндрические координаты в фокальной области, (θ, φ) – сферические угловые координаты на входе фокусирующей системы, B(θ, φ) – функция на входе фокусирующей системы, T(θ) – функция аподизации (для апланатической системы T(θ) = cosθ ), P(θ, φ) – поляризационный вектор, nsin α = NA , NA – числовая апертура системы, n – показатель преломления среды, k = 2π / λ – волновое число, λ – длина волны падающего излучения, f – фокусное расстояние.

В качестве входной функции мы будем рассматривать пучки ГЛ:

Ψ (r,φ)= 1 l!

^lm , σ π ( l + m ) !

[ 2 Л    \1 ™ 1

Г If r 1 Uli r 1.

• -             L exp( im φ ),

2                         l2

2 o jvо j v о ;

где r = sin θ sin α – это безразмерная приведённая радиальная координата на входе фокусирующей системы, σ = sin θ_σ sin α – безразмерный приведённый радиус перетяжки пучка, L_n ^m ( ⋅ ) – обобщённые полиномы Лагерра, l и m – радиальные и угловые индексы соответственно.

Если входная функция имеет угловую зависимость в виде вихревой фазы, как в представлении (2), мы можем упростить интеграл (1):

e ( p , ф , _z ) = - ikf J Q ( p , ф , 6 ) q < e >a e ,               (3)

где q ( θ ) = R_lm ( θ ) T ( θ ) sin θ exp( ikz cos θ ) ,            (4)

R lm ( θ )

X exp

к

sin α l !

sin θσ   π(l + m )

2 sl

2sin 2 6 ) σ

к ^{Sin Q} _o 7

^Ll ^m

Sin 6

к ^sin2 ⁶ = 7

Для апланатической системы форма вектора

Q ( ρ , ϕ , θ ) зависит от поляризации входного поля [3,

5, 8], а его компоненты состоят из суперпозиции функций Бесселя первого рода и разных порядков.

2.    Численное моделирование фокусировки с помощью апланатической системы

Мы используем следующие параметры для расчёта: λ = 1 мкм, f = 101 мкм, sin α = 0,99, n = 1.

Явления взаимодействия фазовых вихрей и поляризации, их трансформации и переход от одного к другой, компенсации или повышение углового момента рассматриваются в сингулярной оптике [17– 23]. Эти явления становятся особенно заметны в условиях острой фокусировки [1–8].

Будем рассматривать вихревые пучки ГЛ с радиальным индексом l =0 и различными угловыми индексами m . Сравнительные результаты для однородной (линейной и круговой) поляризации представлены в табл. 1 в отсутствие вихря и для m = 1, 2 и 5. Приведены картины как полной интенсивности вектора электрического поля | E |², так и отдельно продольной компоненты | E z |², которая становится существенной при острой фокусировке. Также приведены значения полуширины по полуспаду интенсивности (full width at half maximum – FWHM) и площади фокального пятна (half-of-maximum area – HMA).

В отсутствие вихревой фазы (первая строка табл. 1) влияние линейной поляризации заметно лишь в некотором удлинении фокального пятна. Различить направление вращения круговой поляризации в этом случае невозможно.

Наличие вихря первого порядка в падающем пучке (вторая строка табл. 1) существенно меняет фокальную картину. Становится важным не только тип, но и направление вращения круговой поляризации.

В случае вихря второго порядка (третья строка табл. 1) различия в фокальном распределении значительно меньше, и они практически нивелируются при дальнейшем увеличении порядка оптического вихря.

Заметим, что наибольшее влияние состояние поляризации оказывает на картины интенсивности продольной компоненты | E z |², визуальное различие которых является наибольшим при вихревой фазе первого порядка.

При круговой поляризации направление вращения является существенным именно для продольной компоненты. Это связано с тем, что сложение или вычитание поляризационной (спиновой) составляющей углового момента с орбитальной составляющей происходит именно для этой компоненты электрического вектора лазерного излучения.

Чтобы продемонстрировать это более наглядно, внесём астигматическую составляющую exp ( ikx ² 2 f_a ) в падающий пучок. В табл. 2 приведены результаты фокусировки с параметрами: λ = 1 мкм, f =201 мкм, sin α = 0,5, f a = 1000 мкм, n = 1.

Как видно из приведённых результатов, даже в отсутствие вихревой фазы (первая строка табл. 2) состояние поляризации хорошо заметно на картине интенсивности продольной компоненты : для линейной поляризации картина симметрична, а для круговой поляризации наблюдается асимметрия, зависящая от направления вращения (знака) круговой поляризации.

Эффект взаимодействия вихревой фазы (орбитального углового момента) с состоянием круговой поляризации (спиновым угловым моментом) ещё нагляднее в случае наличия вихревой фазы первого порядка (вторая строка табл. 2). Для «+»-поляризации в картине интенсивности продольной компоненты наблюдаются 3 световых пятна, что соответствует общему угловому моменту, равному 2 (т.е. произошло сложение фазового и поляризационного вихрей). Для «-»-поляризации в картине интенсивности продольной компоненты наблюдается 1 явно выраженное световое пятно, что соответствует отсутствию общего углового момента (т.е. произошло вычитание фазового и поляризационного вихрей).

Аналогичная ситуация наблюдается и для больших порядков вихревой фазы: для «+»-поляризации число световых пятен увеличивается на единицу по сравнению с картиной общей интенсивности, а для «-»-поляризации число световых пятен уменьшается на единицу.

Заметим, что картины общей интенсивности в табл. 2 отражают различие только в орбитальном угловом моменте световых пучков (т.е. зависят только от порядка вихревой фазы), а влияние состояния поляризации на них не заметно. Это связано с уменьшением числовой апертуры фокусирующей системы (sin α = 0,5) и, следовательно, с меньшей энергией в продольной компоненте.

3.    Численное моделирование методом FDTD

В работе [23] было показано, что фокусировка лазерного излучения дифракционным аксиконом с высокой числовой апертурой позволяет достичь большей «остроты фокусировки», чем апланатический объектив при одном и том же значении числовой апертуры системы. Поэтому в данном разделе исследуется острая фокусировка вихревых пучков ГЛ на симметричном бинарном аксиконе с использованием метода конечных разностей во временной области (FDTD), реализованном в свободно распространяемом программном продукте Meep [24].

Параметры моделирования: длина волны излучения λ =532 нм, числовая апертура NA ≈ 0,95 (период акси-кона составляет 560 нм). Размер расчётной области x , y,z ∈ [–6,5 λ ; 6,5 λ ].

Табл. 1. Острая фокусировка с помощью апланатической системы

Распределение на входе (интенсивность и фаза)	Распределение интенсивности в фокусе | E |2, | E z |2, размер 10 λ× 10 λ
	Линейная y -поляризация	Круговая «+»-поляризация	Круговая « - »-поляризация
( l, m ) =(0, 0), σ =0,5	•      :	• о	• о
	FWHM( - ) = 0,59 λ FWHM(|) = 0,78 λ HMA=0,36 λ 2	FWHM = 0,69 λ HMA=0,37 λ 2	FWHM=0,69 λ HMA=0,37 λ 2
		• о
( l, m ) =(0, 1), σ =0,4	FWHMz( - ) =0,73 λ FWHMz(|) =0,41 λ HMAz=0,23 λ 2	FWHM = 0,46 λ HMA=0,17 λ 2	FWHMz=0,51 λ HMAz=0,20 λ 2
	О «	о о	о О
( l, m ) =(0, 2), σ =0,35	FWHMz( - ) =0,48 λ FWHMz(|) =0,32 λ HMAz = 0,12 λ 2		FWHMz=0,38 λ HMAz=0,11 λ 2
	о * *	о о	Q о
( l, m ) =(0,5), σ =0,27

Табл. 2. Острая фокусировка с помощью апланатической системы в присутствии астигматической составляющей

Распределение на входе (интенсивность и фаза)	Распределение интенсивности в фокусе E 2 , Ez		2 , размер 40 λ× 40 λ
	Линейная y -поляризация	Круговая «+»-поляризация	Круговая «-»-поляризация
( l, m ) =(0, 0), σ =0,5
О 1 ш ( l, m ) =(0, 1), σ =0,4
ЕН ( l, m ) =(0, 2), σ =0,35
ое ( l, m ) =(0, 5), σ =0,27		^^^^^     -~^*'	^^^г^^     .^^ "

Толщина поглощающего слоя PML – λ , шаг дискретизации по пространству – λ /27, шаг дискретизации по времени – λ /(54 c ), где c – скорость света. Толщина подложки аксикона равна 6,6 λ . Показатель преломления n = 1,46, таким образом, высота микрорельефа составляет 1,087 λ . Радиус пучка σ =0,87 мкм.

Как и в предыдущем параграфе, рассматривается однородная поляризация. Результаты приведены в табл. 3–5. В первых строчках таблиц приведены распределения интенсивности пучков, падающих на фокусирующий аксикон. Изображения входных пучков приведены для малого числа усреднений для демонстрации влияния поляризации и фазовой структуры. Видно, что кольцевая структура не обладает чёткой осевой симметрией, а имеет слабо выраженную чётную симметрию, связанную с порядком вихревой особенности и типом поляризации. Для линейной поляризации это число равно удвоенному порядку вихревой фазы – 2 m (табл. 3), для круговой «+»-поля-ризации число пятен равно 2( m + 1) (табл. 4), и для круговой « - »-поляризации число пятен равно 2( m -1) (табл. 5). Таким образом, уже при распространении на небольшое расстояние (порядка длины волн) в непараксиальном режиме происходит взаимодействие поляризационного и фазового состояний пучка.

Пример распространения мод ГЛ вдоль оси z при круговой « - »-поляризации показан на рис. 1.

а)

Рис. 1. Распространение мод Гаусса–Лагерра вдоль оси z (7,5 λ× 15 λ ): а) (n,m)=(0,1), б) (n,m)=(0,2), в) (n,m)=(0,3)

Наименьшие значения по полуспаду были получены при теневом фокальном пятне для круговой « - »-поляризации (FWHM = 0,31 λ для общей интенсивности и FWHMz = 0,26 λ для продольной компоненты электрического поля) при m = 2. Заметим, что теневое пятно для продольной компоненты получилось на 31,6 % меньше, чем для апланатиче-ской системы (сравните третью строку табл. 1 и третью строку табл. 5). Дальнейшее увеличение m приводит к росту размера фокального пятна, что также можно отметить для других рассмотренных типов поляризации.

Табл. 3. Фокусировка мод ГЛ дифракционным аксиконом с NA = 0,95, линейная поляризация, 15 λ× 15 λ

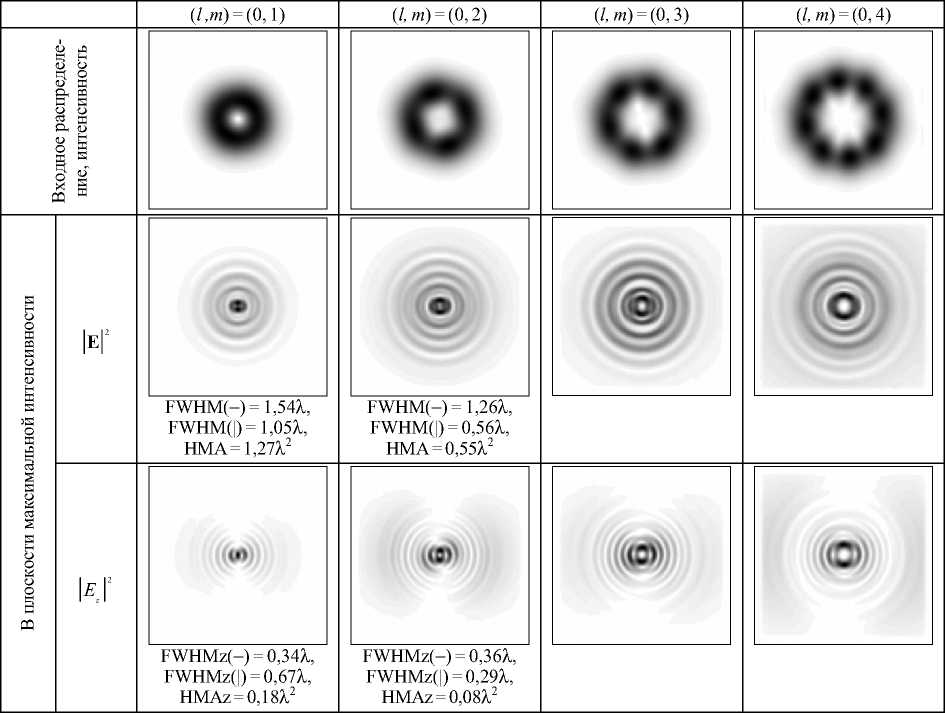
Табл. 4. Фокусировка мод ГЛ дифракционным аксиконом с NA = 0,95, круговая «+» поляризация, 15 1x 15 1

Табл. 5. Фокусировка мод ГЛ дифракционным аксиконом с NA = 0,95, круговая « - » поляризация, 15 1x 15 1

Для линейной поляризации наименьший размер был получен при использовании оптического вихря второго порядка для теневого фокального пятна, причём продольная компонента электрического поля формирует вытянутое кольцо (FWHM( - )=0,36 λ , FWHM(|)=0,29 λ ). Данный результат также демонстрирует лучшую фокусировку аксиконом по сравнению с апланатической системой: для продольной компоненты электрического поля площадь фокального пятна меньше на 33,3%.

Для круговой «+»-поляризации лучший результат был получен при использовании моды ГЛ (0,1): FWHM=0,31λ для общей интенсивности. Следует отметить, что при данном виде поляризации это лучший результат. Теневое фокальное пятно, формируемое продольной компонентой, даже при m =1 существенно боль- ше (FWHMz=0,54λ). С ростом m размер центрального теневого фокального пятна также начинает возрастать.

Также при анализе картин дифракции в плоскости максимальной интенсивности в табл. 4, 5 можно заметить, что размер теневых фокальных пятен для круговой «+»-поляризации при m = 1 и для круговой « - »-поляризации при m =2 совпадают (FWHM = 0,31 λ для общей интенсивности).

В табл. 6 и 7 демонстрируются результаты фокусировки вихревых пучков с внесённой во входной пучок эллиптичностью α :

I x ² + y ² | m exp -          ( x + i α y ) .

( a2 Г

Табл. 6. Фокусировка эллиптичных пучков ГЛ дифракционным аксиконом с NA = 0,95 при (l,m)=(0,1), α = 0,5, 15 λ× 15 λ

Фокусировка эллиптичных пучков ГЛ рассматривалась (6) при m = 1 (табл. 6) и m =2 (табл. 7).

При анализе табл. 6 следует отметить, что при линейной поляризации размер фокального пятна изменился мало (для продольной компоненты электрического поля вообще совпадает), тем не менее характер общей интенсивности в рассматриваемом сечении претерпел заметные изменения. Для круговой «+» поляризации FWHM(-) для общей интенсивности практически совпадают, хотя вместо круглого фокального пятна при α = 1 (табл. 4) мы наблюдаем деформированное световое пятно. Для круговой « - »-поляризации также наблюдается деформация центрального фокального пятна как в общей интенсивности, так и для интенсивности продольной компоненты электрического поля.

Из табл. 7 также видно, что картины дифракции заметно изменились. Фокальное пятно (или кольцо) во всех рассмотренных случаях сильно деформировано. Отметим, что в случае круговой «+»-поляризации наблюдается не провал, как ранее, а деформированное фокальное пятно с FWHM(-) = 0,47λ.

В общем, результаты данного параграфа показывают также существенную зависимость продольной компоненты от поляризационного состояния. Причём эта зависимость хорошо заметна и в картине общей интенсивности, т.к. продольная компонента имеет наибольшую долю энергии при фокусировке аксиконом [25–27].

Заключение

Моделирование апланатической системы в приближении Дебая показало, что добавление оптического вихря существенно изменяет фокальную картину. Становится важным не только тип, но и направление вращения круговой поляризации. Увеличение порядка оптического вихря (>2) приводит к сглаживанию картины дифракции – изображения становятся визуально неразличимы.

Анализ картины интенсивности продольной компоненты электрического вектора светового поля в об- ласти фокуса, особенно при внесении астигматизма, показал, что взаимодействие (сложение или вычитание) поляризационной (спиновой) составляющей уг- лового момента с орбитальной составляющей происходит именно для этой компоненты лазерного излучения.

Табл. 7. Фокусировка эллиптичных пучков ГЛ дифракционным аксиконом с NA = 0,95 при (l, m) = (0, 2), a = 0,5, 15 1 х 15 1

Дальнейшее численное исследование фокусировки с помощью дифракционного аксикона на основе метода FDTD качественно подтвердило результаты, полученные при моделировании фокусировки апла-натической системой в приближении Дебая. Однако количественные результаты показали преимущество дифракционного аксикона перед апланатическим объективом. Численно была исследована дифракция вихревых пучков ГЛ (до 4 вихревого порядка включительно) на осесимметричном бинарном дифракционном аксиконе с числовой апертурой NA=0,95.

Наименьший размер фокального пятна был получен при втором порядке оптического вихря для круговой «–»-поляризации. В этом случае обеспечивается фокусировка в теневое круглое световое пятно, состоящее из поперечных компонент электрического поля. Минимальный размер светового пятна по уровню полуспада интенсивности FWHM = 0,26λ для продольной компоненты электрического поля. Общая интенсивность теневого фокального пятна содержит поперечно-поляризованные боковые лепестки, что уширяет размер пятна до FWHM = 0,31λ.

Работа выполнена при финансовой поддержке гранта РНФ № 14-19-00114.