Особенности преобразования величин в двойственных сетях

Для анализа устойчивого развития, цифровизации исследования сложных систем в условиях перемен, необходимо создавать математические модели технических, экономических систем, которые обеспечивают расчет процессов при изменении структуры. Тензорный метод двойственных сетей позволяет создавать сетевые модели сложных систем. Такие модели представлены в работах Г. Крона [11] и его последователей, а также в работах автора и его коллег [3, 9, 10]. Применению тензорного анализа сетей в инженерных расчетах посвящены работы [3, 5, 8, 11, 12]. Однако тензорный анализ сетей Крона содержал противоречия – постулат об инварианте мощности не выполняется, а применение матриц преобразования путей как группы, вызывало возражения, поскольку при изменении числа замкнутых и разомкнутых путей матрицы прямоугольные, а они не имеют обратных.

В научной дискуссии двадцатого века об инварианте мощности при соединении ветвей в сеть, который постулировал Г. Крон, приняли участие физики и электротехники. В том числе сотрудник А. Эйнштейна Б. Гоффман, а также П. Ланжевен, электротехник Ф. Элджер, тополог П. Росс, основатель кибернетики Н. Винер, А. Душек, Х. Хэпп, отечественные ученые Э.А. Меерович, А.В. Берендеев, В.А. Веников, И.П. Копылов, и другие. Спектр мнений о работах Крона в этой дискуссии, порой выходившей за рамки приличия, автор собрал в книге Тензорная методология в теории систем [1].

Постулат Крона утверждал, что при соединении ветвей мощность в сети не меняется, и на этой основе получал тензорные формулы преобразования величин напряжения и импеданса [2]. Противоречие, вызвавшее споры, состояло в том, что мощность в сети меняется, но расчеты по формулам тензорного анализа сетей дают правильные результаты.

Автор разрешил это диалектическое противоречие путем выхода в другое «измерение» данного вопроса. Оказалось, что при изменении структуры остается постоянной сумма мощностей в двух сетях с двойственной структурой. Выполнение этого закона сохранения потока энергии обеспечивает инвариант двойственности, который состоит в том, что постоянна сумма метрических тензоров двойственных сетей при изменении структуры [3, 5].

Двойственность структуры представляет собой геометрическое свойство пространства, которое связано с физическим свойством потока энергии. Это свойство является развитием того, как геометрические свойства пространства, такие, как однородность, изотропность, связаны с законами сохранения импульса, момента импульса, а однородность времени связана с законом сохранения энергии. Э. Нетер представила это как теорему связи свойств пространства и времени с физикой движения замкнутой системы, а Л.Д. Ландау вывел из принципа наименьшего действия и уравнения Лагранжа [4].

В статье рассматривается изменение физических величин в двойственных сетях при соединении ветвей. Преобразования величин связывает инвариант двойственности, закон, соединяющий физику процессов и двойственность структуры сети, или сетевой модели сложной технической, экономической, биологической системы.

Инвариант двойственности и непланарные графы

Таким образом, инвариант двойственности есть свойство пространства. Казалось бы, проблема постулата Крона об инварианте мощности полностью решена. В общем, это действительно так, однако возникло новое противоречие, связанное с непланарными графами. Это такие графы, которые нельзя изобразить на плоскости без самопересечений. Есть два непланарных графа Куратовского: полный граф на пяти вершинах (K5) и граф «домики и колодцы» (K3,3). Дополнительный интерес состоит в том, что граф K3,3, «домики и колодцы», можно рассматривать как три отрасли, соединенные поставками. В отраслях текут потоки продуктов, а в двойственной сети должны протекать потоки денег. Невозможность представить такую двойственную сеть показывает, что связь потоков продуктов и потоков денег имеет топологическое содержание. Потоки денег, как известно в экономике, двойственные к потокам продуктов, а сеть не существует. Решение этой проблемы важно для моделирования экономических систем.

Теорема Понтрягина-Куратовского доказывает, что если один из этих двух графов есть в структуре любой сложности, то изображение этой структуры без самопересечений выходит за пределы плоскости. Проблема в том, что для непланарного графа нельзя изобразить двойственного графа.

Возникло новое противоречие – инвариант двойственности существует и выполняется. Однако есть такие графы, сети, для которых нет двойственной сети. Тензорный метод с инвариантом двойственности дает решение сети и двойственной сети. Решение существует для сети, изобразить которую нельзя. Это фундаментальная проблема в современной науке.

В.А. Горбатов в 1984 году указал автору, что для непланарного графа, а это графы K 5 и K 33 , двойственный граф не существует. Вместе с тем матрица преобразования путей сети С, а для двойственной сети это ортогональная матрица А = С^-1 t . Эти матрицы являются также матрицами преобразования взаимного базиса путей (двумерных, связанных с поверхностями): А – для данной сети, а С – для двойственной сети.

Возможно, матрица преобразования путей непланарной сети вырожденная? Нет, матрица преобразования существует. Матрицу А сети для графа K 5 автор использовал для построения структуры сети, двойственной к этому непланарному графу. Получилась сеть, похожая на граф K 33 , а для графа K 33 двойственная похожа на K 5 . Но не совсем – в одной сети 9 ветвей, в другой 10 ветвей. Расчеты токов для таких «двойственных» к непланарным графам сетям, показывают, что по законам Кирхгофа в двух узлах одной сети токи выходят, а в другой – входят. Примеры таких расчетов автор рассмотрел в разделе 3.4 [3].

Интересно, что при соединении девяти или десяти ветвей во все более сложные структуры двойственная сеть существует всегда. Но когда девять ветвей соединились в граф

K 33 , а десять ветвей соединились в граф K 5 , двойственная сеть вроде не существует. А при дальнейшем соединении ветвей друг с другом двойственная сеть опять существует.

Это противоречие ждет своего решения.

Преобразование величин в двойственных сетях

Рассмотрим поведение величин воздействий и откликов в сетях с двойственной структурой. Сети состоят из ветвей, которые представляют собой линии, проводники, с границами, узлами.

Величинами в сети являются сопротивления ветвей, токи и напряжения, мощность. Внутренний источник напряжения воздействует в замкнутой сети, откликом является ток в контуре. Внешний источник тока в открытой сети входит извне в одном узле, а покидает сеть в другом узле; откликом является напряжение – разность потенциалов между узлами. Величины в замкнутой сети (базис замкнутых путей) обозначим: e – источник напряжения, Z – сопротивление, ток отклика в контуре ^mi , а напряжение ^me , в ветви ток отклика i c , а напряжение e c . В открытой сети (базис разомкнутых путей): I – источник тока, Y – проводимость напряжение отклика ^jE, ток отклика ^jI, в ветви ток отклика I c , а напряжение E c .

В двойственной сети величины обозначаются подчеркиванием. Замкнутому пути m (mesh – контур) соответствует разомкнутый путь j (junction – узел), и наоборот. Сопротивлению Z соответствует проводимость Y = Z^-1 , и т.д.

В сетях координатами являются пути, которые определяют арифметизацию пространства в структуре. Путь – это линия, проходящая вдоль ветви, как ось координат вдоль измерения. Пути бывают либо замкнутые, либо разомкнутые. Других видов путей нет. Асимметрия состоит в том, что замкнутые пути можно представить разомкнутыми путями, а разомкнутые пути нельзя представить замкнутыми путями.

Двойственность состоит в том, что замкнутому пути в одной сети соответствует разомкнутый путь в двойственной сети, и наоборот. Пути определяют координаты пространства сети, которое состоит из двух ортогональных подпространств замкнутых и разомкнутых путей. При изменении структуры происходит замыкание и размыкание путей, соответственно, меняется размерность их подпространств. Изменение размерности является особенностью преобразования структуры.

Система состоит из элементов, соединенных своими границами. Каждый элемент определяет измерение в пространстве системы. Это пространство существует только в элементах, т.е. является дискретным относительно пространства геометрии, где есть непрерывность, всюду плотность, однородность, изотропность.

Два вида путей, замкнутые и разомкнутые, образуют два независимых, ортогональных подпространства в структуре. При изменениях в структуре замкнутые и разомкнутые пути переходят друг в друга, поэтому меняются размерности их подпространств. Таким образом, в пространстве структуры базисы замкнутых и разомкнутых путей содержат не одинаковое количество элементов.

Замкнутые свободные ветви составляют одну простейшую сеть, а разомкнутые ветви – другую простейшую сеть. Рассмотрим переход к двойственным связанным сетям, расчет откликов приложенные воздействия и мощностей в сетях.

Пусть четыре замкнутые ветви, которые даны на рисунке 1, а слева, соединяются в две сети с двойственной структурой, которые даны справа. Зададим сопротивления Z и проводимости ветвей Y = Z-1 (метрика).

Y = Z-1 =

b i          b₂       e 2 = 2       ^e3 = 1    b⁴

$0) 0Ш

а)

Рис. 1. Сети из четырех ветвей с источниками напряжения и выбранными путями а – сеть из свободных замкнутых ветвей; соединяется в две сети (стрелки пунктиром);

b -связанная данная сеть; c - связанная двойственная сеть

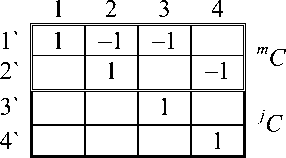
Зададим матрицы преобразования путей в свободных ветвях к путям в связанных сетях, которые выбраны на рисунке. Для сети на рисунке 1.б – это матрица C , для двойственной сети на рисунке 1.в – это матрица C = A = C^-1 t :

A

A

`

1     2    3    4

C ` =

1 `	1				j C	mA
2 `	1	1					(2)
3 `	1		1		m C	jA
4 `	1	1		1

Первые две строки матрицы C представляют матрицу преобразования контуров в сети, mC, она обеспечивает расчет сети с источниками напряжения. Вторые две строки матрицы A представляют матрицу преобразования базисных разомкнутых путей в сети jA, она обеспечивает расчет сети с источниками тока. Эти подматрицы выделены двойными линиями.

Расчет выполняется по формулам тензорного анализа сетей [1,2], с использованием инварианта двойственности. При переходе от свободных замкнутых ветвей с метрикой Z или сети из свободных разомкнутых ветвей с метрикой Y = (Z)^-1 к сети из соединенных ветвей инвариант двойственности имеет вид [3]:

Z c Y + Z Y c = I                                          (3)

где I – единичная матрица. Для двойственной сети этот инвариант имеет вид:

Z Y c + Z c Y = I .                                            (4)

Здесь Z c = ^jA t (^jA Y ^jA t )^{-1 j}A и Y c = ^mC t (^mC Z ^mC t )^{-1 m}C – это матрицы решения, метрические тензоры соединенной сети для разомкнутых и замкнутых путей соответственно. Умножая матрицу решения на вектор воздействия, получаем отклики в ветвях. Это измеримые величины, которые являются результатом расчета сети.

Контурная сеть. Токи в базисных контурах связанной сети для источников напряжения:

^mi^{`</sup> = Y<sup>` m}e ` = (^mC Z ^mC t )^{-1 m}C e 0 .

Токи в ветвях связанной сети i с = ^mC t ^mi – измеримые величины, представляющие решение задачи. Таким образом:

i c = Y c e 0 = ^mC t (^mC Z ^mC t )^{-1 m}C e 0 ,                                  (5)

Напряжения на ветвях связанной сети eс = Z iс. Токи и напряжения на ветвях связанной сети проверяются на предмет выполнения законов Кирхгофа.

Узловая сеть. Источники тока и напряжения в ветвях имеют равную мощность, таким образом, I⁰ = Z^-1 e 0 = Y e 0 . Напряжения в базисных разомкнутых путях связанной сети для источников тока:

^jE^{`</sup> = Z<sup>`} I⁰ ` = (^jA Y ^jA t )^{-1 j}A Y e 0 .

Напряжения в ветвях связанной сети E с = ^jA t ^jE^` – это измеримые величины, представляющие решение задачи. Таким образом:

E с = Z c I⁰ ` = ` ^jA t (^jA Y ^jA t )^{-1 j}A I⁰ ` = ` ^jA t (^jA Y ^jA t )^{-1 j}A Y e 0                                       (6)

Токи на ветвях связанной сети I с = Y E с .

Токи и напряжения на ветвях связанной сети проверяются на предмет выполнения законов Кирхгофа. Для расчета двойственной сети применяются аналогичные матрицы решения с двойственными заменами.

Подставляя формулы расчета величин тока и напряжения в выражение для инварианта двойственности, получим, что по каждой ветви должно выполняться:

e с + E с = e 0 и i с + I с = I⁰ .

Проверим это на примере сети на рисунке 1.

Рассмотрим расчет токов и напряжений в контурной и узловой сети. Зададим источники напряжения в отдельных ветвях.

1            2            3            4

e 0 =        1            2            1            2                                (7)

Источники тока в ветвях, имеющие такую же мощность, равны I⁰ = Z^-1 e 0 = Y e 0

	1	2	3	4
I0 =	0,5	2	0,333	1	(8)

Выполняя действия в матрице решения Y c для заданных источников напряжения, получим токи и напряжения отклика в ветвях соединенной контурной сети:

	1	–0,353	1	–0,706
i c =	2	0,235	e c =    2	0,235
	3	0,353	3	1,059
	4	0,118	4	0,235

Выполняя действия в матрице решения Z c для заданных источников напряжения, получим токи и напряжения отклика в ветвях узловой соединенной сети:

	1	0,853	1	1,706
I c =	2	1,765	E c =    2	1,765
	3	–0,020	3	–0,059
	4	0,882	4	1,765

Проверим выполнение инварианта двойственности: для токов i с + I с = I⁰ .

	1	–0,353	1	0,853		0,5
i c	2	0,235	+   I c    2	1,765	=	2	= I0
	3	0,353	3	–0,020		0,333
	4	0,118	4	0,882		1

А также выполнение инварианта двойственности для напряжений : e с + E с = e 0 :

1	–0,706	1	1,706		1
e c    2	0,235	+   E c   2	1,765	=	2	= e 0
3	1,059	3	–0,059		1
4	0,235	4	1,765		2
Можно видеть, что инвариант двойственности выполняется.

Рассмотрим аналогичные вычисления для двойственной сети. Получим отклики – токи в ветвях и напряжения на ветвях для источников напряжения и тока. Когда в данной сети свободные ветви замкнутые, как показано на рисунке 1, то в двойственной сети свободные ветви разомкнутые, как показано на рисунке 2.

Рис. 2. Сети из четырех ветвей с источниками тока и выбранными путями а – сеть из свободных разомкнутых ветвей; соединяется в две сети (стрелки пунктиром); b –связанная данная сеть; c – связанная двойственная сеть www.rypravlenie.ru

том 18 № 1 (54), 2022, ст. 1

С учетом отношений между величинами двойственных сетей, о которых сказано выше, получим отклики в ветвях двойственной сети при контурном и узловом воздействии. Для этого зададим источники токов и напряжений с учетом двойственных замен.

Рассмотрим расчет токов и напряжений в контурной и узловой сети. Зададим источники напряжения в отдельных ветвях. e 0 = Z^-1 e 0 = Y e 0

1	2	3	4
e 0 =     0,5	2	0,333	1                                    (9)
Источники тока в ветвях, имеющие такую же мощность, равны I 0 = Z -1 e 0 = Y e 0
1	2	3	4
I 0 =       1	2	1	2                             (10)

Выполняя действия в матрице решения Yc для заданных источников напряжения, получим токи и напряжения отклика в ветвях соединенной двойственной. При этом значения токов и напряжений меняются местами относительно исходной сети. Для контурной сети:

1	0,853
e c =   2	1,765
3	–0,020
4	0,882

1	1,706
i c =     2	1,765
3	–0,059
4	1,765

Выполняя действия в матрице решения Zc для заданных источников напряжения, получим токи и напряжения отклика в ветвях узловой соединенной двойственной сети:

	1	–0,353	1	–0,706
E c =	2	0,235	I c =    2	0,235
	3	0,353	3	1,059
	4	0,118	4	0,235

Инвариант двойственности выполняется в двойственной сети для токов i с + I с = I ⁰ .

	1	–0,353	1	0,853		0,5
E c	2	0,235	+ e c    2	1,765	=	2	= e 0
	3	0,353	3	–0,020		0,333
	4	0,118	4	0,882		1

А также инвариант двойственности выполняется для напряжений : e с + E с = e 0 :

	1	–0,706	1	1,706		1
I c	2	0,235	+    i c     2	1,765	=	2	= I 0
	3	1,059	3	–0,059		1
	4	0,235	4	1,765		2

Можно видеть, что инвариант двойственности выполняется также в двойственной сети. При этом значениям токов в двойственной сети соответствуют значения напряжений, как для внешних источников тока, так и для внутренних источников напряжения.

том 18 № 1 (54), 2022, ст. 1

Круговая диаграмма распределения мощности между контурными и узловыми подсетями в данной сети в двойственной сети опубликована автором еще в 1985 году [1]. На это круговой диаграмме получаем, что «контурная» мощность в данной сети равна «узловой» мощности в двойственной сети. И, наоборот, «узловая» мощность в данной сети равна «контурной» мощности в двойственной сети.

Перемножая соответствующие токи и напряжения по ветвям в каждой из четырех рассмотренных сетей, и суммируя, получим мощности. В контурной сети мощность на ветвях равна ^mP c = e c * i c = 0,706, в узловой сети мощность равна ^jP c = E c * I c = 6,128.

Можно видеть, что мощность источников напряжения в сети из свободных ветвей ^m P 0 равна сумме мощностей в контурной и узловой сети ^mP 0 = ^mP c + ^jP c = 0,706 + 6,128 = 6,834.

В силу двойственности аналогичные значения имеем в двойственной контурной и узловой сети, а именно, ^m P c = 6,128, ^j P c = 0,706. Представим полученные значения в соответствующие секторы на диаграмме мощности [3].

Рис. 3. Диаграмма изменения мощности в двойственных сетях при изменении структуры

Таким образом, мощность в узловой сети равна мощности в контурной двойственной сети, а мощность в контурной сети равна мощности узловой двойственной сети. Соответственно, равны токи и напряжения на ветвях в этих сетях, с той разницей, что токи в сети равны напряжениям в двойственной сети, а напряжения в сети равны токам в ветвях в двойственной сети.

том 18 № 1 (54), 2022, ст. 1

Покажем это на рассмотренном примере. На рисунке 4 показано, что контурные токи в данной сети численно равны узловым напряжениям в двойственной сети.

а – контурные токи в сети; b – узловые напряжения в двойственной сети

На рисунке 5 аналогично показано, что контурные напряжения в данной сети численно равны узловым токам в двойственной сети.

а - контурные напряжения в сети; b - узловые токи в двойственной сети

Аналогичные отношения, как нетрудно видеть, существуют между узловыми напряжениями в данной сети контурными токами в двойственной сети, а также узловыми токами в данной сети и контурными напряжениям в двойственной сети.

Заключение

Рассмотренные особенности преобразования величин в двойственных сетях необходимо принимать во внимание при создании и применении сетевых моделей сложных технических, экономических систем в условиях цифровизации и быстрых изменений технологий.

Следует также еще раз подчеркнуть, что поступательные движения в пространстве происходят по разомкнутым путям, вращательные движения происходят по замкнутым путям. Любое движение можно представить комбинацией поступательного и вращательного движения. Таким образом, замкнутость и открытость являются фундаментальными свойствами в геометрии и физике. Однако для структуры систем важным является переходы между разомкнутыми и замкнутыми путями, преобразование путей, поскольку при этом изменяется размерность подпространства, свойства структуры, и протекающих в ней процессов. Геометрическая целостность состоит в том, что взаимно дополняющие преобразования происходят в двойственной сети, двойственном пространстве.

Инвариант двойственности является свойством пространства структуры, также как однородность, изотропность. Система из элементов, сеть имеет свойство двойственности. В системе возникают процессы как отклики на приложенные воздействия. Потоки процессов возникают в подпространстве замкнутых путей, или разомкнутых путей. Эти процессы не зависят друг от друга, поскольку подпространства ортогональны.

Соответствие между замкнутыми и разомкнутыми путями в двойственных сетях имеет не только структурный, геометрический, но и физический смысл. Замкнутому пути в одной сети соответствует разомкнутый путь в двойственной сети, а разомкнутому пути в одной сети соответствует замкнутый путь в двойственной сети.

Движение в пространстве, как известно, можно разложить на поступательное и вращательное движение. Тогда в двойственном пространстве составляющей поступательного движения должно соответствовать вращательное движение, а составляющей вращательного движения должно соответствовать поступательное движение.