Особенности причинно-следственных связей в технологических системах

В соответствии с [1] технологическая система (ТС) - это совокупность функционально взаимосвязанных средств технологического оснащения, предметов производства и исполнителей, предназначенная для выполнения в регламентированных условиях производства заданных процессов или операций в соответствии с требованиями нормативной документации. В многочисленных исследованиях, например, в [2], ТС рассматривается как оператор преобразования одного или нескольких исходных продуктов, как входных воздействий, в выходной продукт, рассматриваемый в качестве реакции системы.

Проведенные нами исследования показали, что существуют некоторые особенности причинно-следственных связей, влияющие неявным образом на реакции ТС [3]. Эти особенности представляются существенными в практическом отношении. Анализу их и посвящена данная работа. Рассмотрим вначале трактовки основных понятий, используемых при описании причинно-следственных связей в ТС.

Согласно [4], фактор - это причина, движущая сила какого-либо процесса, явления, определяющая его характер или отдельные черты. В рамках такого определения понятия "фактор" и "причина" неразличимы. Тем не менее, различия существуют, и имеет смысл выявить их на уровне определений, приведенных в других литературных источниках. Так, в [3] под причиной понимается явление, действие которого вызывает, определяет, производит или влечет за собой другое явление, которое называется следствием. В науке на нынешнем этапе причинноследственные связи классифицируются по разным признакам. В частности, по числу и связности воздействий они делятся на простые, составные, однофакторные, многофакторные, системные и внесистемные [3]. Эта идея классификации не позволяет рассматривать понятия "фактор" и "причина" как семантически совпадающие. В общем случае причина шире, чем фактор. Более того, одновременное действие группы факторов может обусловить возникновение причины, не сводимой ни к одному из них. В качестве примера многофакторных причин можно сослаться на зависимость отходов при вязании штучных изделий Q от отходов, связанных с сырьем - Qc, отходов, обусловленных техническим состоянием машины, и отходов Qр, вызванных действиями работницы. Каждая из величин Qc, Qм, и Qр выступает как представитель своего множества факторов, могущих и не пересекаться с двумя другими, вследствие чего возникают основания рассматривать их как многофакторные причины по отношению к величине Q. Рассмотрим теперь общую картину причинно-следственных отношений в ТС.

В соответствии с общепринятыми представлениями свяжем независимость от времени отображающих их параметров со стационарностью. С практической точки зрения стационарные условия обычно отождествляются с устойчивым состоянием ТС.

Выясним, какой при стационарности ТС оказывается картина причинноследственных связей между ее параметрами. Пусть

Y = f(X i ), (1)

где: Y – реакция системы, X i – определяющие ее факторы ( i = 1,2,...k). Для моделирования функции (1) используем полиномы, широко применяемые в научных исследованиях и практике в легкой промышленности [2]. Используем вначале линейную модель. При аппроксимации (1) моделью вида

Y = b 0 + b 1 X 1 + b 2 X 2 + ... + b n X n (2)

видим что величину Y , определяют n факторов. Естественно, дисперсия Y полностью объясняется дисперсией факторов X i . Это самый простой вид многофакторной зависимости, но даже он таит в себе далеко не очевидные особенности. На рис. 1 изображены фазовые портреты систем (2), построенные по методике, представленной в [5], при n = 3 и двумя различными плотностями распределения факторов X 1 , X 2 , X 3 . Рисунок показывает, что положение аттракторов систем [5], т.е. областей максимального сгущения фазовых точек, в обоих случаях диаметрально противоположное. Естественно, такой эффект достигнут при определенном подборе функций распределения. Однако он убедительно показывает, что даже если форма модели (2) статична, то изменения функции распределения факторов способны, тем не менее, вызвать кардинальные изменения поведения системы. Отсюда следует, что без учета функций распределения возможных значений факторов мы проходим мимо важной особенности, содержащей в себе очень существенную информацию по отношению к ТС. Пусть, например, Y – величина отходов на стадии производства конкретного продукта. Тогда фазовый портрет на рис. 1а соответствует хорошо отлаженной ТС, т.к. ее аттрактор расположен в области минимальных значений отходов. Напротив, ТС с фазовым портретом на рис. 1б стремится к производству максимального уровня отходов, а потому нуждается в более активном управлении. В [6] показано, что в обоих случаях система может оставаться устойчивой, меняется лишь положение притягивающего множества ее состояний. Однако в реальных условиях параметры ТС неизбежно изменяются во времени, переводя систему в нестационарный режим. Нестационарность может проявляться в изменении коэффициентов модели, описывающей систему, факторного состава правой части модели ТС, ее порядка. Следовательно, в нестационарных условиях речь должна идти о непрерывной перестройке модели по мере изменения ситуации в технологической системе. Иными словами, в нестационарных условиях имеет смысл говорить об адаптивной модели [7].

Математическая модель технологической системы в форме полинома некоторой степени выступает как нечто гораздо большее, чем заменитель ее на период исследования. В нестационарных условиях, когда порядок аппроксимирующего полинома может изменяться, в соответствии с ним будут изменяться и причины изменений состояния системы. Чем выше порядок аппроксимирующего полинома, тем шире набор влияющих на систему причин. В табл. 1 представлена зависимость числа членов полиномиальной модели 2-го и 3-го порядков от числа факторов. Как видно из этой таблицы, в случае полинома 2-ой степени относительно трех факторов имеем три линейных эффекта, три квадратичных, три кубичных, три эффекта парного взаимодействия и семь эффектов взаимодействия 3-го порядка. В итоге обнаруживается 19 потенциальных источников воздействий на технологическую систему. Кроме того, как показано в [6], кубическая форма содержит условия для возникновения бифуркаций состояния системы, что способно намного усложнить ее поведение, создавая условия для скачкообразных изменений состояния системы. При увеличении числа факторов количество членов моделей 2-го и 3-го порядков быстро растет. Табл. 1 показывает, что увеличение числа факторов лишь с 2 до 5 приводит к росту числа членов полиномиальной модели 2-го порядка с 5 до 20, а 3-го – с 9 до 55.

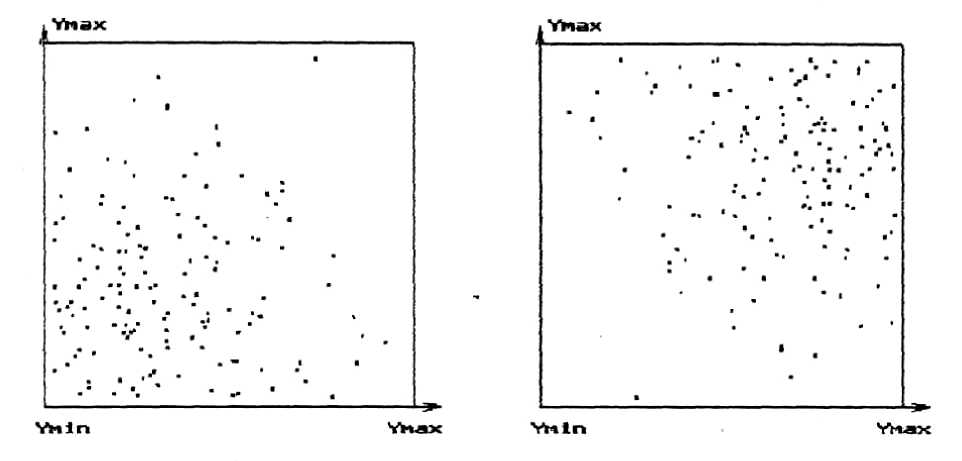
а)                                            б)

Рисунок 1 – Фазовые портреты технологических систем, описываемых (2) при n =3 и двух различных плотностях распределения возможных значений факторов

• X 1 , X 2 и Х 3

Таблица 1 – Зависимость числа членов в полиномиальной модели 2-го и 3-го порядков от числа факторов

№ п/п	Число факторов	Число членов в полиноми а льной мо д ели
		второго порядка	третьего пор я дка
1	2	5	9
2	3	9	19
3	4	14	34
4	5	20	55

Из теории планирования эксперимента и з вестно, что эффекты взаимодействия факторов формально можно устранить п у тем математических преобразований модели. Однако в этом случае новые независимые пере м енные теряют в наглядности, а порой и в физическом смысле. Рассмотрим, на п ример, неполную полиномиальную модель второго порядка от н осительно двух факторов:

Y = b 1 X 1 + b 2 X 2 + b 12 X 1 X 2 .                     (3)

Преобразуя переменные, ее нетрудно привести к виду, содержащему лишь квадратичные члены, образованные новыми переменными Z 1 и Z 2 :

Y = B 0 + B 1 Z 1² + B 2 Z 2² .                          (4)

Между тем, исходная форма модели (3) информативнее. В форме (4) мы видим квадратичную зависимость Y от каждого фактора, в то время как (4) указывает на то, что нелинейность порождается совместным действием обоих факторов. Форма (3) представляет как бы суперпозицию трех источников воздействий на выходной параметр Y . Эффект парного взаимодействия влияет на выходной параметр наравне с факторами X 1 и X 2 , играя роль третьего фактора. Однако тот факт, что количественно он выражается через первичные факторы, не позволяет безоговорочно идентифицировать его как настоящий фактор. Однако ничто и не вынуждает делать это. Достаточно привлечь термин "виртуальный", широко распространенный, в частности, в физике и информатике.

И все же, что может дать это понятие, кроме терминологической унификации? Прежде всего, отметим, что причинно-следственная картина производственных связей при использовании такого терминологического инструментария предстает в виде базиса, образованного первичными факторами и своего рода надстройки из виртуальных факторов. В этой связи уместно обратить внимание на то, что эффекты взаимодействия факторов не есть следствие математического формализма, обусловленного применением моделей именно полиномиального типа, а действительный феномен, имеющий под собой физическую основу. Приведем пример.

При работе трикотажной машины уровень обрывности зависит от многих факторов. Выделим среди них входное натяжение нити и длину нити в петле. Очевидно, что кроме их действия по отдельности присутствует эффект зависимости влияния одного из них от того, на каком уровне находится другой. Так, при одинаковых средних значениях натяжения нити и его дисперсии колебания натяжения нити будут чаще приводить к обрывам при меньшей длине нити в петле, чем при большей. Налицо эффект физического парного взаимодействия факторов, несводимый к простому суммарному их действию.

В заключительном примере воспроизведем следующую ситуацию. Пусть реакция системы описывается функцией времени Y(t) . Примем, что эта функция зависит от двух факторов X 1 (t) и X 2 (t). Т.е.

Y(t) = F{X 1 (t), X 2 (t)} . (5)

Придадим функции Y(t) вид неполного полинома второго порядка, а X 1 (t) и X 2 (t) запишем в виде гармонических функций времени. Тогда зависимость (5) примет вид:

• Y(t) = B 0 + B 1 Sin ωt + B 2 Cos ωt + B 12 Sin ωt Cos ωt

или: Y(t) = B 0 + B 1 Sin ωt + B 2 Cos ωt + B 3 Sin 2ωt . (6)

Модель (6) хорошо описывает колебания натяжения нити при сматывания с трехконусной бобины с крестовой намоткой. Она показывает, что в соответствующей нелинейной системе в спектре Y(t) кроме гармоники с круговой частой ω, обусловленной действием факторов X 1 и X 2 , присутствует гармоника с частотой 2ω, соответствующая третьему – виртуальному фактору. Обратим внимание на то, что, влияя по отдельности на Y , ни фактор X 1 , ни фактор X 2 не в состоянии в принципе привести к удвоению частоты воздействия на выходной параметр. А это – довод в пользу его автономности и целесообразности идентификации его как фактора виртуального.

Рассматривая множество факторов, определяющих состояние технологической системы, можно обнаружить признаки существования факторов еще одного типа. Формальной предпосылкой их возникновения является кластеризация исходного множества факторов, которую нетрудно выявить специальными математическими приемами. По отношению к каждому кластеру имеет смысл поставить вопрос:

"Нельзя ли факторы каждого кластера рассматривать как аргументы некоторой функции?" При положительном ответе на поставленный вопрос открывается возможность замены исходного набора факторов меньшим числом функций от них, т.е. построения более экономного по числу характеристик описания состояния технологической системы. В этом заключается основная идея факторного анализа. В его рамках функции от некоторого набора исходных переменных получили название общих или латентных (скрытых) факторов [8]. Ситуации, в которых появляются скрытые факторы, отнюдь не редки. Например, при использовании пряжи одного и того же волокнистого состава и удовлетворяющей требованиям одного и того же стандарта, но полученной от разных поставщиков, могут выявиться различия в ее технологической надежности, обусловленные различиями в молекулярной структуре полимера волокон, из которых пряжа состоит. Действие скрытого фактора, в качестве которого выступает функция распределения, демонстрируют фазовые портреты на рис.1.

Таким образом, в любой технологической системе возможно существование виртуальных и латентных факторов, приводящих к возникновению особых многофакторных причин изменения ее состояния. Как правило, им не соответствует прямой физический или технический аналог, и они не всегда различимы на фоне действительных факторов. Они усложняют технологическую систему, и без их учета видимая картина причинно-следственных связей может оказаться далеко не полной и не дающей возможности провести исчерпывающий анализ состояния системы. В условиях производства это неизбежно ведет к не вполне адекватным решениям по управлению системой в конкретной ситуации. Поэтому дальнейшие исследования в данном направлении, на взгляд автора, представляют существенный практический интерес.