Особенности применения абсолютной и относительной ошибки аппроксимации в регрессионном анализе

Разработка эконометрических

моделей является

целью

эконометрического анализа, позволяющая спрогнозировать тенденции развития экономических процессов для принятия обоснованных решений. Эконометрические модели позволяют выявить особенности функционирования объекта и благодаря этому предсказать будущее его поведение при изменении какого-либо параметра. Для любого субъекта возможность прогнозирования ситуации значит получение наилучших результатов, избежание потерь, минимизация рисков. Построение эконометрических моделей с целью анализа и прогнозирования экономических процессов является важной задачей при проведении исследования любого уровня. Однако проблема оценки качества полученной модели является ключевой в моделировании.

Оценка значимости как уравнения в целом, так и отдельных его параметров проводится после того как уравнение регрессии найдено. Значимость уравнения регрессии – это установление соответствия математической модели, выражающей зависимость между переменными, эмпирическим данным и определение достаточного количества включенных в уравнение объясняющих переменных для описания зависимой переменной. При подборе уравнения тренда, значение ошибки аппроксимации может служить для выбора наиболее подходящего уравнения. Аппроксимация результатов наблюдений может идти по разным моделям, но наилучшей аппроксимацией является та, в которой минимально отклонение между моделью и реальными данными в относительных значениях.

Фактические значения результативного признака отличаются от теоретических значений, рассчитанных по уравнению регрессии, т. е. у и yx. Чем меньше эти отличия, тем ближе теоретические значения к эмпирическим данным, тем лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака (у - yx) по каждому наблюдению представляет собой ошибку аппроксимации. Их число соответствует объему совокупности. В отдельных случаях ошибка аппроксимации может оказаться равной нулю. Отклонения (у - yx) несравнимы между собой, исключая величину, равную нулю. Для сравнения используются величины отклонений, выраженные в процентах к фактическим значениям.

Отклонения (у - y x ) можно рассматривать как абсолютную ошибку аппроксимации. Поскольку (у - y_x) может быть как величиной положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю. Относительная ошибка аппроксимации рассчитывается по формуле:

l^l * 100 (1)

Чем ближе измеренное значение к истинному значению, тем точнее измерение. Если экспериментальное значение меньше реального, то абсолютная ошибка отрицательна, а если экспериментальное значение больше реального, то абсолютная ошибка положительна.

Таким образом, величина отклонения теоретического значения результативного признака от фактического значения, взятая по модулю, представляет собой абсолютную ошибку аппроксимации. А величина, равная отношению абсолютной ошибки к фактическим значениям результативного признака, выраженная в процентах, является относительной ошибкой аппроксимации.

Для иллюстрации приведены данные опроса шести семей (в которой два работающих взрослых и один ребенок) г.Самара по связи расходов на продукты питания с уровнем доходов этих семей.

Таблица 1 - Данные опроса

Расходы семьи на продукты питания, y, руб/месяц	Доходы семьи, x, руб/месяц
8000	21000
18000	50000
10000	23000
15000	40000
11000	27000
12000	30000

На основе поля корреляции можно сделать предположение, что связь между доходами и расходами на продукты питания – линейная.

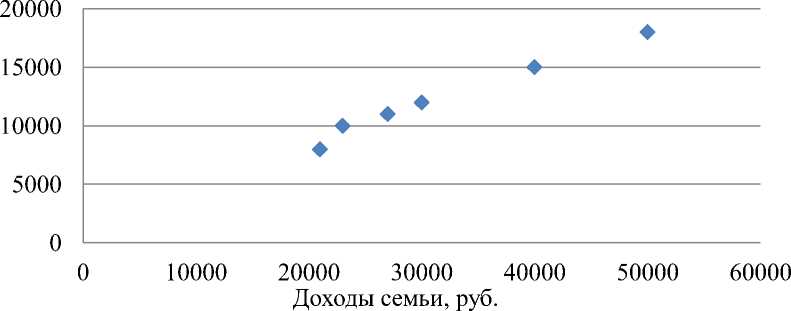
Рисунок 1 - Поле корреляции по данным опроса

Предположительно зависимость является линейной, поэтому получены следующие параметры линейного уравнения парной регрессии.

b = 0,322112

a = 2079,451

А уравнение парной регрессии для представленных данных будет следующее:

5£ = 2079,451 + 0,322112 * x

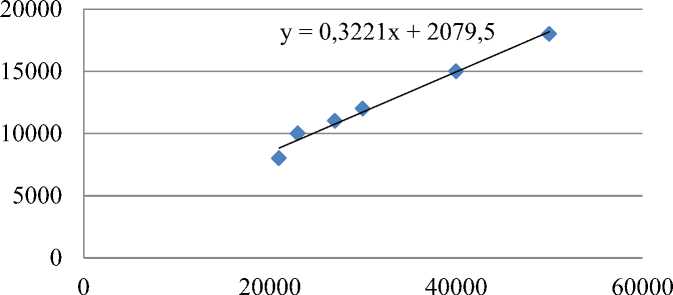
Доходы семьи, руб.

Рисунок 2 - Поле корреляции и линия тренда

Из уравнения можно сделать вывод, что с увеличением доходов семьи на 1000 рублей, расходы на питание увеличиваются на 322,112 рублей.

Таблица 2 - Расчет абсолютной, относительной, средней ошибки аппроксимации

	x	y	x*y	x²	y²	ŷx	y-ŷx	|y-ŷx | /y*100
1	21000	8000	168000000	441000000	64000000	8843,8	- 843,8	10,5
2	50000	18000	900000000	2500000000	324000000	18185,0	- 185,0	1,0
3	23000	10000	230000000	529000000	100000000	9488,0	512,0	5,1
4	40000	15000	600000000	1600000000	225000000	14963,9	36,1	0,2
5	27000	11000	297000000	729000000	121000000	10776,5	223,5	2,0
6	30000	12000	360000000	900000000	144000000	11742,8	257,2	2,1
Итого	191000	74000	2555000000	6699000000	978000000	74000,0	-	21,1
Ср. знач	31833,3	12333,3	425833333,3	1116500000	163000000	12333,3	-	3,5

Таким образом, средняя ошибка аппроксимации A = 3,5%, что говорит о хорошем качестве уравнения регрессии, т.е. свидетельствует о хорошем подборе модели к исходным данным и показывает, что линия регрессии хорошо приближает исходные данные.

На основе проведенного расчета можно сделать следующие выводы. Чем ближе измеренное значение к реальному значению, тем точнее измерение. Абсолютная ошибка является недостаточно показательной. Поэтому нагляднее точность измерения будет характеризоваться отношением абсолютной ошибки к полученному значению измеренной величины, а именно относительная ошибка. Если в ряде данных имеются значения y, близкие к нулю, то значение абсолютной ошибки аппроксимации также становится чрезмерно завышенным вне зависимости от адекватности построенной модели. Кроме того, если значение y x имеет значение равное нулю или близко к нулю, то, относительная ошибка аппроксимации перестает учитывать разницу между фактическим и расчетным значениями — под знаком суммы получается единица. А также, если фактические данные ряда имеют очень большие значения, то есть измеряются в тысячах единиц, то знаменатель становится очень большим, в результате чего средняя ошибка аппроксимации существенно занижается, вне зависимости от качества построенной модели.

Таким образом, можно сделать вывод, что объективно оценить качество модели только по абсолютной, относительной ошибкам аппроксимации не представляется возможным, так как абсолютная ошибка зависит от выбора масштаба измерения, а относительная ошибка завышает вклад ошибки вблизи нулевого значения.