Особенности применения пакета MATLAB/Simulink для анализа статической устойчивости синхронных генераторов в энергосистеме

Введение. Сегодня активно вводятся в эксплуатацию новые электростанции, на которых применяются мощные установки комбинированного типа. В Челябинской области в последние годы были введены в эксплуатацию два парогазовых блока мощностью 430 МВт на ЮжноУральской ГРЭС-2, три парогазовые установки мощностью 250 МВт на Челябинской ГРЭС и пылеугольный блок мощностью 660 МВт на Троицкой ГРЭС. Строительство новых электростанций приводит к увеличению перетоков мощности и росту уровня токов короткого замыкания в электроэнергетической системе, что ужесточает требования к способностям синхронных генераторов сохранять статическую и динамическую устойчивости в нормальных и аварийных режимах.

Задаче анализа режимов синхронных генераторов, работающих параллельно с энергосистемой, в разное время было посвящено много работ, при этом особое внимание всегда уделялось анализу их устойчивости на математических моделях, реализуемых с применением программных средств на ЭВМ [1–10]. Поэтому при моделировании элементов и объектов электроэнергетики широкое применение находят разные математические пакеты, в частности MATLAB/Simulink [11–20]. Его возможности позволяют рассчитывать установившиеся и переходные режимы в электрических цепях с различными функциональными элементами, включая электродвигатели, трансформаторы, линии электропередачи, синхронные генераторы, а также рассматривать вопросы управления ими. Так, в [13, 15] затронуты вопросы разработки синхронных генераторов новой конструкции, выполнено имитационное моделирование в MATLAB/ Simulink, дана оценка их характеристик. Работы [11, 12] посвящены вопросам моделирования нормальных и аварийных режимов синхронных генераторов, в частности, анализу статической и динамической устойчивости при изменении нагрузки, коммутациях в сети и коротких замыканиях, а в работах [14, 16, 17] рассмотрены вопросы настройки систем управления генераторами и их влияние на устойчивость отдельных агрегатов и энергосистемы в целом. Результаты, достигнутые в этих работах, позволяют сформировать представление о возможностях пакета MATLAB/Simulink в решении задач имитационного моделирования, что в свою очередь поддерживает интерес к его дальнейшему изучению.

Однако применение пакета для имитационного моделирования сопряжено с рядом трудностей. Реализованные в пакете модели силовых элементов, таких как генераторы, трансформаторы, ли- нии электропередачи и др., зачастую построены на основе схем замещения, отличающихся от общепринятых и описанных в отечественной литературе либо требующих специфических знаний и навыков при задании их параметров в программе. Например, в [11] проводится сравнение упрощенной модели синхронного генератора «SSM» из пакета MATLAB/Simulink с математической моделью, реализованной в программе Mustang, нередко используемой в службах диспетчерского управления при анализе статической и динамической устойчивости. Авторы статьи отмечают существенные отличия как в логике построения моделей, так и в перечне задаваемых параметров. А в [18] затронута проблема правильного ввода параметров силовых трансформаторов и приведены необходимые для этого выражения. Учитывая это, сохраняют свою актуальность вопросы изучения особенностей применения пакета MATLAB/Simulink для имитационного моделирования в задачах расчета и анализа режима объектов электроэнергетической системы и оценка соответствия полученных результатов расчетам, выполненным общеизвестными способами.

В данной работе на примере блока ЮжноУральской ГРЭС-2 рассмотрена задача оценки статической устойчивости синхронного генератора, работающего через цепь передачи параллельно с энергосистемой. Для этого первоначально был выполнен расчет установившегося режима сети и определена угловая характеристика активной мощности генератора. Затем была сформирована имитационная модель в пакете MATLAB/Simulink и выполнена параметризация ее элементов с учетом особенностей схем замещения и их реализации в программе, после чего проведено моделирование и сравнение потоков мощностей, напряжений в узлах и угловых характеристик активной мощности генератора. Основные этапы и результаты выполненной работы приводятся ниже.

Математическая модель цепи передачи. На Южно-Уральской ГРЭС-2 установлено два блочных синхронных генератора SGEN5-2000H мощностью 430 МВт (505 МВА) каждый, подключенных с шинам напряжением 220 кВ и выдающих в сеть мощность по четырем воздушным линиям электропередачи. Поэтому в качестве первоначальной задачи была рассмотрена оценка устойчивости одного синхронного генератора SGEN5-2000H при его работе через повышающий трансформатор ТНЦ-630000/220 и двухцепную линию 220 кВ на эквивалентную энергосистему напряжением 110 кВ через условный трансформатор связи мощностью 2500 МВА.

Принципиальная схема такой цепи передачи приведена на рис. 1. Она включает в себя синхронный генератор, повышающий трансформатор, воздушную линию электропередачи, условный трансформатор связи и эквивалентную энергосистему. На схеме линия электропередачи выполнена двойной или двухцепной. Связь линии с энергосистемой осуществляется через условный трансформатор с параметрами, получающимися путем эквивалентирования схемы внешней сети. При анализе устойчивости генераторов схема подключения реальной электростанции может быть сведена к рассматриваемой цепи передачи путем преобразований, как отмечено в работах [1–4].

Расчёт установившегося режима в схеме проводился в относительных единицах при отключенном АРВ генератора с учетом отбора активной мощности на собственные нужды. Схема замещения цепи передачи приведена на рис. 2. Параметры элементов на схеме замещения рассчитывались при базисном напряжении U _Б = 115 кВ и базисной мощности S _Б = 1000 МВА и приведены в табл. 1.

СГ         Т1

Л1

Л2

Т2         ЭС

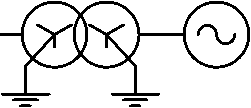
Рис. 1. Схема цепи передачи: СГ – синхронный генератор; Т1 – повышающий трансформатор; Л1–2 – линии электропередачи; Т2 – условный трансформатор связи; ЭС – энергосистема

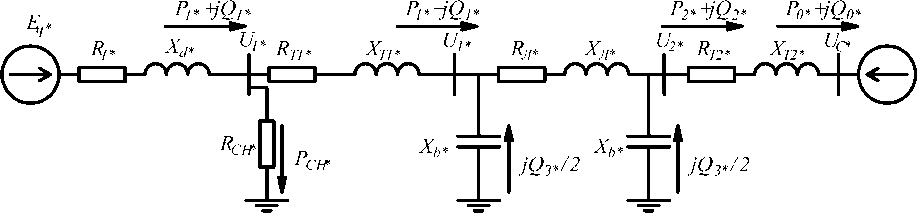
Рис. 2. Схема замещения цепи передачи

Напряжение и мощности в конце цепи передачи в долях базисных величин задавались равными UC* = 0,957 , Р0* = 0,416 и Q0* = 0,19 соответственно. При этом ЭДС генератора и выдаваемые им мощности составили Eq * = 2,495, Р0* = 0,43 и Q0* = 0,261, что соответствует его номинальным мощностям при напряжении на выводах, равном UГ* = 1,057 .

Таблица 1

Параметры схемы замещения цепи передачи

Параметры элемента	Параметры схемы замещения
Синхронный генератор
Р Г = 429 МВт; cos ф Г = 0,85; гГ = 0,0029; x d = 1,9065 о.е.; x' d = 0,3628 о.е.	А г = ^- =   9 = 505; cos ф Г 0,85 S          1000 X d * = x d ■ А Б = 1,9065 ■ "505" = 3,775; X' , = x' ■ А Б = 0,3628 ■ 1000 = 0,718; d *     d S Г            505 R , = r ■ А Б = 0,0029 ■ 1000 = 0,005743 Г* Г S Г            505
Собственные нужды генератора
Р СН = 7 МВт	Р , = P H =     = 0,007 СН*    S Б    1000
Трансформатор Т1
А Т1 = 630 МВА; U внном = 242 кВ; U ннном = 20 кВ; u K1 = 12,5%; А Р К = 1208,11кВт	u K1 S Б 12,5 1000 X T1 === 0,198; Т1* 100 S T1    100 400 R , = А Р К ■ А Б ю-3 = 1208,11 •1000 ■ю- 3 = 3,044 ■ю- 3 ; Т1       S T12                630 2 k Т1 = и ВНном = 242 = 12,1 U ННном    20
Линия 220 кВ
r 0 = 0,054 Ом/км; x 0 = 0,328 Ом/км; b 0 = 3,47 - 10-6 См/км; L = 50 км	R E* = 1 r ■ L ■ А" = 1 ■ 0,054 ■ 50 ■ 1000 = 0,026; Л 2    2 0     U Л2    2           230 2 X , =1 x ■ L ■     = 1 ■ 0,328 ■ 50 ■ 1000 = 0,155; 2 0     U Л2 2           230 2 Хь * = —--- А =---- 1^--1000 = 108,954; b 0 ■ L и Л2    3,47 ■Ю "6 ■ 50 230 2 _      2       2 Qv =---=------= 0,018 З* Xb *    108,954
Трансформатор Т2
А Т2 = 2500 МВА; и ВНном = 230 кВ; U ННном = 115 кВ; u K2 = 11,5%; А Р К = 4600 Вт	X T2 .= U K2- ■ 9^ = 115 . Ж = 0,046; Т2*   100 S T2    100 2500 RT2 ^А Р кЗ ^ б ^0 - 3 = 4600 ■ 10 00 ■ 10 - 3 = 4,36^0 - 4 ; Т2      S T22             2500 2 U ВНном 230 к т э —         —    — 2 T2 U ННном 115

Для рассматриваемой модели цепи передачи угловая характеристика активной мощности генератора (УХАМ) при отключенном АРВ с учетом активных сопротивлений описывается выражением:

_  Eq² .       E q * • U C*

P r* ( 5 ) = ——sin a_n + —-----sm( 5-a_n ), (1)

Z 11*              Z 12*

где Z _11* и Z _12* – собственное и взаимное сопро-

тивления цепи передачи; a 11 и a₁₂ - соответствующие сопротивлениям углы; δ – угол цепи передачи.

При работе генератора с АРВ пропорционального действия (АРВ ПД) выражение (1) может быть преобразовано к виду:

E ' *²

^р г*^{( 5 )} = "^~^{sin a} 11 ⁺

Z 11*

+ E ’ q * • U C* • C0S( 5 q -5 ' q )

Z 12*

sin( 5-a ₁₂ ) -

U _C2_* ---

X,*-X' d *       d *

2   |pr*+ jXd *+ Zs*| • |pi

Г*

^{+ jX}' d *⁺ ^ Z s *|

sin 2 5 , (2)

где E ' _q * , 5 ' _q - переходная ЭДС генератора и соответствующий ей угол цепи передачи; Z _z , -

полное эквивалентное сопротивление относительно выводов генератора.

После преобразования схемы замещения и подстановки значений ее параметров в приведенные выше выражения УХАМ при отключенном АРВ принимает вид:

Р Г (5) = 8,56 + 584 sln(5 - 0,179°), МВт,     (3)

а при работе с АРВ ПД:

Р _Г(5) = 34,12 + 1059sin(5 -1 , 128°) -

-327,8sin2 5 , МВт.                      (4)

Полученные выражения необходимы при анализе статической устойчивости синхронного генератора, так как позволяют судить об условиях его работы и проводить оценку этих условий путем вычисления и сравнения запасов.

Имитационная модель в пакете MATLAB/ Simulink. Первоначально была собрана математическая модель, общая блок-схема которой приведена на рис. 3. Для этого использовались математические элементы из основной библиотеки «Simulink» и элементы, моделирующие процессы в трехфазных цепях, из дополнительной библиотеки «SimPowerSystems».

На рис. 3 синхронный генератор «SG» моделируется трехфазным элементом «Simplified Synchronous Machine pu Units (SSM)». На входы «Pm» и «E» подаются константы, отвечающие за мощность на валу ротора и ЭДС генератора. Отбор мощности на собственные нужды генератора «AP» выполнен элементом «Three-Phase Series RLC Load». Для моделирования трансформаторов «T1» и «Т2» применены элементы «Three-Phase Transformer», выполненные в двухобмоточном исполнении со схемами соединения обмоток, как показано на рис. 1. Двухцепная линия представлена в модели двумя параллельными элементами «Three-Phase PI Section Line», обозначенными как «L1» и «L2». В качестве энергосистемы «PS» применен элемент «Three-Phase Source», представляющий собой трехфазный источник питания c неизменной ЭДС.

Измерение режимных параметров цепи в модели реализовано блоками «S1»–«S4». Логическая схема для одного такого блока показана на рис. 4. На схеме по мгновенным значениям фазного тока и фазного напряжения вычисляются действующее значение линейного напряжения U ( t ) и величины активной P ( t ) и реактивной Q ( t ) мощностей, протекающих в цепи.

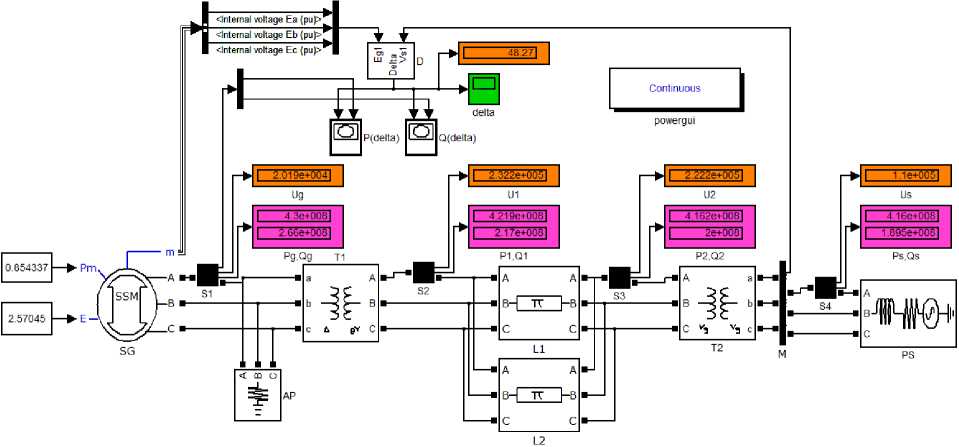
Рис. 3. Модель исследуемой цепи в пакете MATLAB/Simulink

Для измерения угла δ собран блок «D», логическая схема которого представлена на рис. 5. В блоке угол цепи передачи «Delta» вычисляется как угловая разница между ЭДС генератора «Eg1» и напряжением энергосистемы «Vs1» с учетом фазосдвигающего действия повышающего транформатора «Т1». Вычисление углов реализовано через блок «3-Phase Sequence analyzer», выделяющий амплитуду и фазу составляющей прямой последовательсти основной частоты.

Для удобства величины напряжений в узлах цепи передачи и активной и реактивной мощностей в её ветвях, измеряемые посредством блоков «S1»–«S4», выводятся на экран через элементы «Display». С целью визуализации зависимостей мощностей цепи передачи от угла δ использованы графические элементы «XY scope».

Моделирование в MATLAB/Simulink проводилось в два этапа. Первоначально с помощью блока «powergui» (кнопка «Load Flow and Machine Initialization») рассчитывался установившийся режим сети и определялись режимные параметры синхронного генератора, при этом задавались либо активная мощность и напряжение на его выводах, либо его активная и реактивная мощности, как показано на рис. 6. Затем выполнялся расчет мгновенных значений токов и напряжений в обмотках элементов схемы и других параметров в зависимости от времени.

Особое внимание было уделено вопросам выбора и задания параметров элементов имитационной модели, поскольку это представляет наибольший интерес и оказывает существенное влияние на сходимость расчета и результаты моделирования.

Особенности параметризации отдельных элементов. В библиотеке «SimPowerSystems» синхронный генератор может моделироваться системами дифференциальных уравнений разных порядков [21]. Наиболее детализированная модель генератора строится на системе уравнений 7-го порядка, получаемой путем предварительных преобразований общеизвестной системы уравнений Парка-Горева, дополненной уравнением движения ротора генератора. Такая модель позволяет проводить углубленный анализ переходных процессов, учитывать влияние демпферных обмоток, а также появление в цепях генератора составляющих токов разных частот. Для анализа статической и динамической устойчивости в пакете предлагается упрощенная модель генератора 3-го порядка с меньшим числом уравнений «Simplified Synchronous

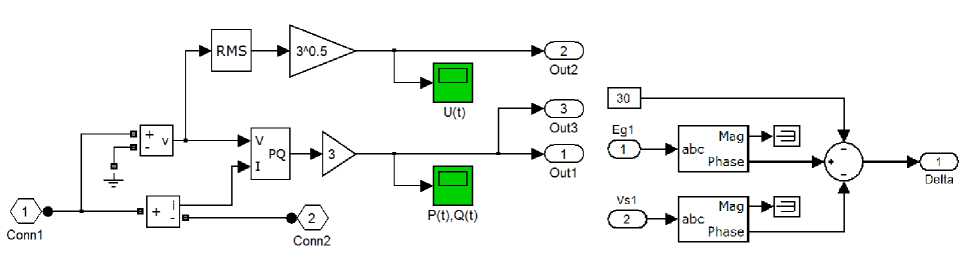
Рис. 4. Блок измерителя мощности и напряжения в электрической цепи

Рис. 5. Блок измерителя угла δ цепи передачи

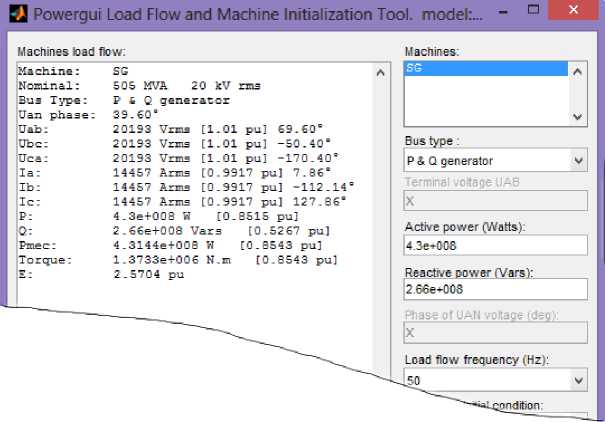
Рис. 6. Окно инициализации параметров генератора в блоке «powergui»

Machine pu Units (SSM)». Эта модель пренебрегает высшими гармониками и влиянием демпферных контуров, поэтому она была использована в данной работе. Параметры, введенные для генератора в модели, приведены в табл. 2.

В качестве индуктивного сопротивления ге- нератора задавалось синхронное индуктивное сопротивление Xd. Коэффициент демпфирования и постоянная инерции задавались в соответствии с рекомендациями из работы [11]. При этом по- следняя величина рассчитывалась через момент инерции следующим образом:

T J   2,74 ⋅ GD ² ⋅ω ² ном

H=  = ном

2,74⋅250,67⋅30002

= = 7,226 с, 2⋅429⋅106

где T_J – постоянная инерции всего агрегата, с; GD ² – момент инерции, т∙м²; P _ном – номинальная активная мощность генератора, Вт; ω_ном – номинальная частота вращения ротора, об/мин.

Параметры силовых трансформаторов из «SimPowerSystems» задавались в соответствии с рекомендациями, предложенными в работе [18].

При этом для упрощения моделей не учитывалось насыщение их магнитопроводов («Saturable core») и соответственно характеристики намагничивания для них не задавались («Saturation Characteristic»). Параметры элементов вводились в относительных единицах в соответствии с табл. 3.

Отметим, что при задании параметров в относительных единицах индуктивности каждой из обмоток трехфазного трансформатора совпадают с их индуктивными сопротивлениями и для двухобмоточных элементов определяются путем деления пополам напряжения короткого замыкания u _К . При этом активные сопротивления обмоток могут быть найдены по выражению:

1 ∆ P К ⋅ 10 ^{- 3}

R= ⋅ ном где ∆Pk – потери короткого замыкания, кВт; Sном – номинальная полная мощность трансформатора, МВА.

Активное сопротивление R m и индуктивность L_m цепи намагничивания в табл. 3 определялись с учетом того, что в моделях MATLAB/Simulink данная цепь представляется параллельным соеди-

Таблица 2

Параметры синхронного генератора «SG»

Параметр	Ед. изм.	Значение
Номинальная полная мощность «Pn(VA)»	ВА	505·106
Номинальное напряжение «Vn(Vrms)»	В	20·103
Частота «fn(Hz)»	Гц	50
Постоянная инерции «H(sec)»	с	7,226
Коэффициент демпфирования «Kd(pu_T/pu_W)»	–	10
Число пар полюсов «p»	–	1
Активное сопротивление «R(pu)»	о.е.	0,0029
Индуктивное сопротивление «X(pu)»	о.е.	1,9065

Таблица 3

Параметры силовых трансформаторов «Т1» и «Т2»

Параметр Ед. изм. Значение «Т1» «Т2» Номинальная полная мощность, «Pn(VA)» ВА 630·106 2500·106 Частота, «fn(Hz) Гц 50 50 Параметры стороны ВН Схема соединения – Yg Yg Номинальное напряжение, «V2 Ph-Ph(Vrms)» В 242·103 230·103 Активное сопротивление, «R2(pu)» о.е. 0,00192/2 0,00184/2 Индуктивность, «L2(pu)» о.е. 0,125/2 0,115/2 Параметры стороны НН Схема соединения обмоток – Delta(D11) Yg Номинальное напряжение, «V1 Ph-Ph(Vrms)» В 20·103 115·103 Активное сопротивление, «R1(pu)» о.е. 0,00192/2 0,00184/2 Индуктивность, «L1(pu)» о.е. 0,125/2 0,115/2 Параметры цепи намагничивания Активное сопротивление, «Rm(pu)» о.е. 2680 106 Индуктивность, «Lm(pu)» о.е. 1235 106 нением этих элементов в отличие от схем замещения, описанных в отечественной литературе. Искомые величины в относительных единицах могут быть найдены следующим образом:

R = 5 ном     L = 100

m A P o .10 - 3 , m     1 0 ’

_ 2 R i + R o    _2 L i + L o    _R - R

R S =     3    , ^L S =     3    , R m =    3   ,

L m

^L 0 ^- L 1

Cp

= C 1 , C g

3 C 1 C 0

где A P 0 - потери холостого хода, кВт; 1 ₀ - ток холостого хода, %.

Ввиду малого влияния этих величин на потоко-распределение мощностей в схеме замещения, показанной на рис. 2, в математической модели, рассмотренной ранее, они не учитывались. В свою очередь в имитационной модели с этой же целью значения R_m и L_m трансформатора связи «Т2» приравнивались к 10⁶.

Модель трехфазной линии электропередачи «Three-Phase PI Section Line», реализованная в «SimPowerSystems», учитывает взаимоиндуктив-ные связи между проводами фаз, их емкостную связь с землей и поэтому требует ввода удельных параметров, таких как активные сопротивления прямой и нулевой последовательностей R ₁ и R ₀, индуктивностей этих последовательностей L ₁ и L ₀ и емкостей C ₁ и C ₀, соответственно.

Схема замещения линии с учетом всех трех фаз показана на рис. 7, а. Параметры на схеме связаны следующими соотношениями:

C 1

—

C ₀

Из соотношений, принятых в программе, следует, что при моделировании симметричных режимов работы схемы параметры нулевой последовательности следует задавать равными параметрам прямой. Тогда схема замещения упрощается до однолинейной, показанной на рис. 7, б. На схеме r _s — R m = R 1 и L_S — L_m = L 1 , что соответствует ее общеизвестному представлению в расчетах установившихся режимов. В случае моделирования несимметричных режимов, например, несимметричных коротких замыканий, величину L ₀ следует скорректировать с учетом наличия грозозащитного троса на линии и его параметров. Например, используя коэффициент X ₀ X ₁ из работы [22].

Также отметим, что в случае превышения длиной линии 50 км ее сопротивления автоматически корректируются программой по гиперболическим функциям.

Параметры, введенные для линий «L1» и «L2», даны в табл. 4.

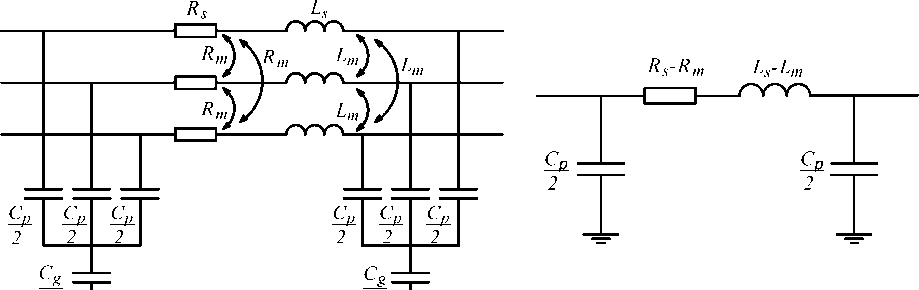
2 ^-                   2 ^_

а)                                                                  б)

Рис. 7. Cхемы замещения линии электропередачи: а – трехфазная схема; б – однолинейная схема

Параметры линий электропередачи «L1» и «L2»

Таблица 4

Параметр	Ед. изм.	Значение
Частота, fn(Hz)	Гц	50
Активное сопротивление ПП, R1(Ohms/km)	Ом/км	0,054
Активное сопротивление НП, R0(Ohms/km)	Ом/км	0,204
Индуктивность ПП, L1(Н/km)	Гн/км	1,044·10–3
Индуктивность НП, L0(Н/km)	Гн/км	2∙1,044·10–3
Емкость ПП, С1(F/km)	Ф/км	11,09·10–9
Емкость НП, C0(F/km)	Ф/км	11,09·10–9
Длина линии, (km)	км	50

В табл. 5 показаны значения параметров, задававшиеся при параметризации эквивалентной энергосистемы «PS», представленной в работе элементом «Three-Phase Source». Для элемента в программе указывается мощность трехфазного короткого замыкания на его выводах и соответствующее ей базисное напряжение. Так как в математической модели энергосистема была представлена источником бесконечной мощности, то для исключения влияния внутреннего сопротивления энергосистемы в программе её мощность короткого замыкания задавалась как большое значение, при котором сопротивления были бы пренебрежимо малы.

Параметры элемента «Three-Phase Series RLC Load», моделирующего отбор мощности на собственные нужды генератора, вводились в соответствии с табл. 1, при этом указывалась активная мощность, номинальное напряжение и частота сети.

Оценка результатов моделирования. Первоначально в собранной в программе схеме была выполнена проверка соответствия напряжений в узлах и потоков мощностей в ветвях значениям, рассчитанным по математической модели. Для этого в пакете были заданы номинальные активная и реактивная мощности синхронного генератора P 0 = 430 МВт и Q 0 = 266 МВар , как было показано на рис. 6, и выполнен расчет установившегося режима. Полученные значения и результаты их сопоставления приведены в табл. 6.

Из сравнения результатов видно, что разница значений не превысила 1%. При этом стоит отметить, что номинальная величина ЭДС генератора в модели составила Eq * = 2,57, это на 2 % больше расчетной величины. Из этого следует, что наибольшее отличие режимных параметров будет обусловлено моделью синхронного генератора и особенностями её реализации в MATLAB/Simulink.

Далее, варьируя параметр «Pm» в имитационной модели, соответствующий мощности на валу ротора генератора, была снята угловая характеристика активной мощности при отключенном АРВ. Для каждого значения активной мощности, выдаваемой генератором, рассчитывался установившийся режим и фиксировалось значение угла δ. При этом ЭДС возбуждения «E» в каждой точке была одинакова и равна номинальной. По полученным в итоге точкам строилась экспериментальная зависимость активной мощности генератора от угла δ, показанная на рис. 8, а. Там же приведена и расчетная кривая, получающаяся по выражению (3).

Кривая из программы проходит несколько ниже расчетной зависимости, различие между ними не превышает 4% при угле 5 = 90 ° , что в дальнейшем будет определять величину различия запасов статической устойчивости синхронного генератора, найденных по этим кривым.

В завершении было выполнено моделирование режимов работы генератора с сохранением неизменного напряжения на выводах путем регулирования его ЭДС. Для этого при каждом значении активной мощности, выдаваемой генератором, рассчитывался установившийся режим, однако, ЭДС возбужения не была постоянной, а каждый раз пересчитывалась из условия, что напряжение на выводах элемента остается равным номинальному. В результате была построена кривая, пока-заная на рис. 8, б, схожая по своей траектории с УХАМ генератора, полученной ранее по выражению (4) для АРВ ПД. Из сравнения графиков видно, что принципиальное отличие между кривыми

Таблица 5

Параметры эквивалентной энергоcистемы «PS»

Параметр	Ед. изм.	Значение
Линейное напряжение, (Vrms)	В	110·103
Начальный сдвиг фазы «А», (degrees)	град. эл.	0
Частота, fn(Hz)	Гц	50
Режим нейтрали	Yg
Мощность трехфазного короткого замыкания, (VA)	ВА	1013
Базисное напряжение, (Vrms Ph-Ph)	В	110·103
Отношение X/R	–	7

Таблица 6

Сопоставление результатов имитационного моделирования с результатами расчетов по математической модели

Узел	P , МВт		Q , МВар		U , кВ
	MATLAB	Расчёт	MATLAB	Расчёт	MATLAB	Расчёт
S1	430,00	430,00	266,00	261,00	20,19	20,09
S2	421,90	422,00	217,00	217,00	232,20	232,27
S3	416,20	416,00	200,00	201,00	222,20	222,22
S4	416,00	–	189,50	–	110,00	–
Δ, %	0,024		0,793		0,178

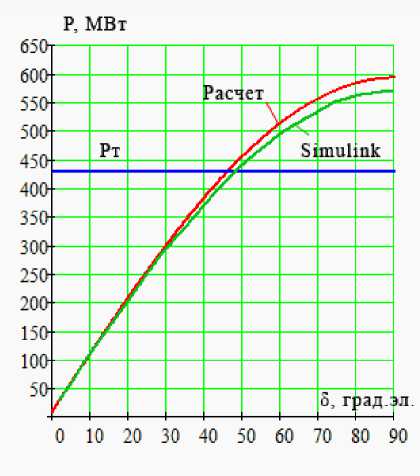
а)

Рис. 8. Угловые характеристики активной мощности: а – при отключенном АРВ; б – при АРВ ПД

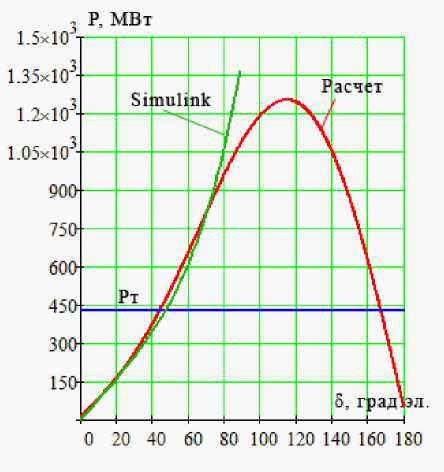
б)

начинается только при углах 5 >  80 ° , а при меньших углах разница несущественна или практически отсутствует.

Заключение

В процессе выполнения работы были достигнуты следующие результаты.

• 1.    В пакете MATLAB/Simulink собрана имитационная модель цепи передачи, включающая синхронный генератор, линию электропередачи, силовые трансформаторы, модули измерений и рассмотрены особенности их реализации.

• 2.    Выполнено моделирование установившего режима и проведено сравнение режимных параметров и угловой характеристики активной мощности синхронного генератора, полученных в модели, с рассчитанными классическим способом.

• 3.    Рассмотрены особенности параметризации отдельных элементов в пакете MATLAB/Simulink, показан пример ввода параметров и даны некоторые рекомендации.

Таким образом, результаты работы будут полезны при изучении особенностей применения пакета MATLAB/Simulink в решении задач моделирования установившихся и переходных режимов электроэнергетических систем.