Особенности проектирования содержания практических занятий по теории механизмов и машин

Выполненные ранее исследования Е. П Грошевой [3] и других исследователей [2] по проектированию содержания общетехнических дисциплин позволили сформулировать конкретные требования к содержанию общетехнической дисциплины «Теория механизмов и машин» (ТММ), в том числе в ее практической части, направленной на развитие творческих способностей, основными среди которых являются: 1) содержание общетехнической дисциплины в соответствии с поставленной целью формируется и реализуется через структурные компоненты методической системы – целевой, содержательный, процессуальный и диагностический; 2) содержание общетехнической подготовки, должно формироваться на основе интеграции дисциплины ТММ, сопутствующих дисциплин естественнонаучного, общетехнического и специального циклов и самостоятельной работы в условиях квазипрофессиональной инновационной деятельности; 3) учебные дисциплины общетехнической подготовки в техническом вузе должны рассматриваться в единстве содержательного и процессуального компонентов; 4) в содержании дисциплины ТММ, как и в содержании других общетехнических и сопутствующих дисциплин, фундаментальное научное и техническое знание должно быть представлено в единстве, при этом первое составляет его инвариантную часть, второе - варьируемую; 5) содержание варьируемой части дисциплины ТММ должно быть связано с содержанием профессиональной и специальной подготовки студентов втузов для определения содержания варьируемого (профессионально направленного) материала; 6) содержание курсов общетехнических дисциплин следует группировать вокруг фундаментальных физических и научнотехнических теорий, что позволяет реализовать целостность профессионального образования; 7) учебно-методический комплекс должен включать, наряду с традиционными структурными элементами (рабочие программы, учебно-методический материал лекций и т. п.), систему информационно-компьютерной поддержки курса в виде электронных учебников, пакетов прикладных программ и других программных средств, позволяющую студентам втузов самостоятельно получать знания и умения по дисциплине и осуществлять самоконтроль уровня усвоения материала.

В связи с вышеперечисленным рассмотрим непосредственно вопросы конструирования содержания дисциплины ТММ. В соответствие с дидактической моделью учебного предмета, предложенной И. К. Журавлевым и Л. Я. Зориной [2], она включает два блока - основной и процессуальный. В основной блок входит содержание дисциплины, имеющее непосредственное отношение к ней. А в процессуальный - дополнительные материалы, обеспечивающие усвоение знаний, формирование различных умений, компетенций, а также развитие и воспитание обучающихся. Для обучения ТММ в основной блок включаются предметные знания, а в процессуальный - комплекс вспомогательных знаний (логических, методологических, философских, историко-научных, межпредметных, оценочных).

Таким образом, в основной блок содержания ТММ по разделу «Кинематический анализ механизмов» можно включить нижеследующий материал [4; 5].

Современные машины включают в себя механизмы, образованные группами Асура 2-го класса, всех пяти видов, а также группами более высоких классов, обеспечивающими движение выходных звеньев с требуемыми кинематическими параметрами. Для определения их величин достаточно удобен графоаналитический метод, предусматривающий построение планов скоростей и ускорений. Рассмотрим некоторые предпосылки к использованию этого метода.

Планом скоростей (ускорений) называется такое построение [1], при котором векторы абсолютных скоростей (ускорений) выходят из одной точки, называемой полюсом. Они обладают рядом свойств [4]: 1) векторы, выходящие из полюса плана представляют в определенном масштабе абсолютные скорости (ускорения) точек механизма; 2) векторы, соединяющие концы векторов абсолютных скоростей (ускорений), представляют в определенном масштабе относительные скорости (ускорения) точек механизма; 3) все неподвижные точки механизма лежат в полюсе плана; 4) отношение относительной скорости (касательного ускорения) к соответствующей длине звена есть угловая скорость (ускорение) этого звена; 5) фигуры, образованные векторами на плане подобны фигурам, составленным звеньями механизма и сходно с ними расположенные.

Планы строятся для конкретного положения механизма, изображенного в масштабе, в следующей последовательности: 1) задается закон движения ведущего звена, обычно принимается за основу, что оно вращается равномерно; 2) строится план скоростей группы Асура, непосредственно присоединенной к ведущему звену и стойке; 3) строится для этой же группы план ускорений; 4) строятся планы скоростей и ускорений следующей присоединенной группы, так продолжается до тех пор, пока не будут построены планы скоростей и ускорений всех групп механизма [5].

Задача кинематического анализа механизма считается полностью решенной, если для каждого звена механизма известны положения, скорости и ускорения двух его точек, или -положение, скорость и ускорение одной точки и угловая координата, угловая скорость и угловое ускорение самого звена. Для облегчения решения этой задачи в таблице приведены схемы построения планов для структурных групп 2-го класса всех 5-ти видов и пояснения к ним.

Процессуальный блок рассмотрим на примере определения скорости и ускорения точки М 2 методом планов [5] для механизма, изображенного на рисунке 1, при следующих исходных данных: угловая скорость вращения кулисы ан = 100 рад/с; длина коромысла АВ 1 ав = 0,6м; длина отрезка 1 ам = 0,3м. Для этого построим планы скоростей и ускорений. Составим векторные уравнения. Скорость точки А 1 вычислим по формуле V а = а • l_OA = 100 • 0,3 = 30 м / с.

В масштабе проведем вектор Pa , перпендикулярно звену ОА и направленный в сторону вращения кулисы 1.

Скорость точки А 2,з найдем из графического решения системы векторных уравнений

V A2 — V A3 — V A1 + V A2A1

// ОА

V A3 — V B + V A3B = 0   1 АВ

Из точки a i плана проводим линию параллельную звену ОА, из полюса проводим линию перпендикулярную звену АВ , на пересечении получаем точку а 2, 3 .

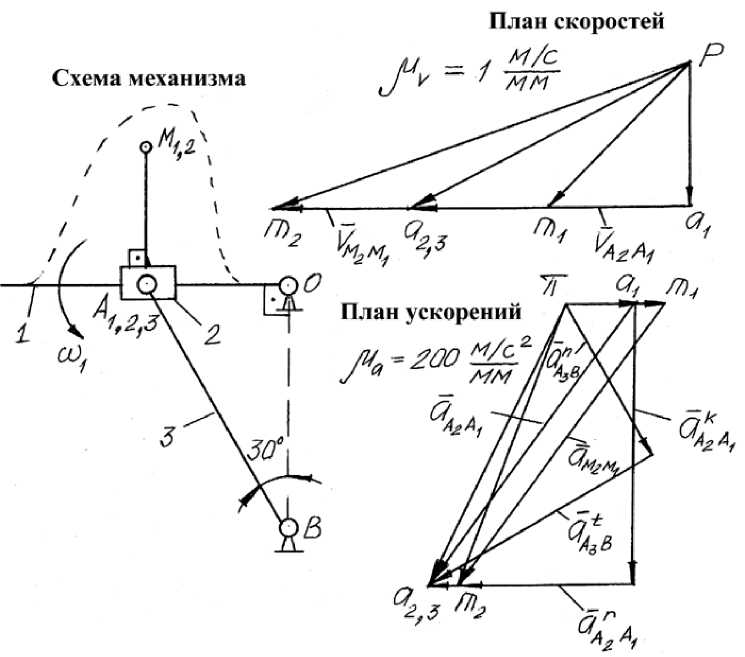
Рис.1. Построение планов скоростей и ускорений.

Для определения скорости точки   М2   вычислим скорость точки vМ^ = ^ .lOM = 100.0,3/cos450 = 42,4м/с и изобразим ее на плане. Скорость точки М2 найдем из графического решения векторного уравнения vМ2 = vМ1 + vМ2М], скорость v М2М1 = v А2А1 как скорости поступательного движения 2-го звена.

Из построенного плана определим скорости точки М 2 и относительной скорости точки А 2 относительно точки А 1

vм2 = pm2 • ^ = 92 -1 = 92 м/ с;   vлгЛ = ага2 • ^ = 60 -1 = 60 м / с

Построим план ускорений, вычислим ускорение точки А 1

а л, = rf • l_OA = 100² • 0,3 = 3000 м / с ²

Ускорение точки А2,3 определим из графического решения системы векторных уравнений: Кr аА2 = аА1 + аА2А1 + аА2А1 ЮА    // ОА              I nt алз = аВ + алзВ + а А3В       ,

=    J

// АВ     1 АВ

К где а^^ = 2 • щ • vaa = 2-100 ■ 60 = 12000 м/с2  - кариолисово ускорение, имеет направление вектора v A A повернутого на 900 в сторону вращения кулисы;

r aA A – релятивное ускорение;

а\ в = v A 3- = 67- = 7490 м / с²

l_AB   0,6

–

нормальное ускорение,

направлено к центру

вращения;

t аА В– касательное ускорение.

м / с ²

Выберем масштаб построения ^ = 200----, в этом масштабе вычисленные a      мм ускорения      будут      выражены      отрезками      следующей      длины:

|а^ | = 15 мм ;    а КК, 1 = 60 мм;  \а n _B| = 37,5 мм .

Построив соответствующие вектора, определим ускорение точки А 23 , а л2 = п а з ^. ^ е =

68 . 200 = 13600 м/с2.

Вычислим ускорение точки М 1 а м = щ ² • l = 100² • 0,3/cos 45 0 = 4240 м покажем с ²

этот вектор на плане. Местоположение точки М 2 определим из графического решения системы векторного уравнения.

^аМ2 = ^аМ1 + ^аМ2М1, где а М2М1 = а А2А1

Из построенного плана определим искомое ускорение точки    М 2

ам2 =nm2 • ца = 64 • 200 = 12800 м/ с2.

Ответ: v м₂ = 92 м / с ; а м₂ = 12800 м / с ².

Описанный метод определения кинематических параметров (скорости и ускорения) позволяет для такого сложного механизма, достаточно просто и наглядно вычислить искомые параметры, что особенно важно в прикладных задачах механики.

Таким образом, проектирование содержания общетехнических дисциплин на основе сформулированных положений и включением в его состав двух блоков (основного и процессуального) обеспечивают соблюдение следующих дидактических принципов: принцип действенности знаний, принцип наглядности обучения, принцип связи теории с практикой обучения и др., а также способствуют развитию творческого потенциала студентов.