Особенности прогнозирования временных рядов с помощью SPLUNK

Современное общество – информационное общество, а значит, не мыслит себя без средств передачи, хранения и обработки информации. Стремительное развитие сети Интернет и информационных технологий в целом привело к тому, что на данный момент все: люди, компании, фирмы, государственные и коммерческие учреждения имеют свои программные и аппаратные решения для ведения бухгалтерских отчётов, средств журналирования событий, сбора рабочей информации и обработки запросов пользователей. Всё это создаёт невероятно плотный трафик и заполняет хранилища информации. В данной статье к рассмотрению предлагается инструментарий аналитического комплекса «Splunk».

Целью работы является определение модели, при использовании которой получается наиболее точно предсказать изме- нение трафика на краткосрочном периоде, а также получение сглаживания наблюдаемой кривой без потери промежуточных точек и скрытия пиковых значений.

Главным преимуществом работы с этим комплексом является возможность оперировать временными рядами. В свою очередь это означает возможность как исследовать любые процессы, так и оперировать ими. В том числе, определять поведение систем в краткосрочной перспективе. Чтобы немного упростить процесс работы с инструментами «Splunk», мы решили разобраться какие модели линейной регрессии, в связке с фильтром Калмана, обеспечат наиболее точные прогнозы поведения. Данный опыт может быть полезен тем, кто занимается мониторингом процессов, не имеющих значительных изменений на всём промежутке наблюдений, например:

• -    мониторинг интернет-сетей провайдеров;

• -    мониторинг функционирования сетей предприятий;

• -    мониторинг процессинга банковских фирм;

• -    исследований тенденции обращений в медицинские учреждения.

Рассмотрим несколько базовых определений, необходимых для понимания протекающих процессов и сути применения различных фильтров.

Временные ряды

Под временным рядом понимают индексированную последовательность точек данных, отражающих развитие во времени некоторого процесса, зафиксированных через равные промежутки времени.

Целью прикладного анализа временных рядов является построение математической модели ряда, с помощью которой можно объяснить поведение ряда и прогнозировать значения его состояний. Если временной ряд нестационарен, то сначала выделяют и удаляют нестационарную его составляющую. Процесс удаления этих компонент может проходить в несколько этапов, на каждом из которых рассматривается ряд остатков, полученных в результате вычитания из исходного ряда подобранной модели [1]. После исключения неслучайных компонент временной ряд должен стать стационарным. Предположение о том, что после выделения неслучайных компонент ряд остатков является стационарным рядом, очень существенно для анализа временного ряда. На практике, однако, такая ситуация далеко не всегда имеет место.

После того, как ряд приближен к стационарному обычно подбирают модель полученного стационарного процесса. Цель этого этапа - описание и учет в дальнейшем анализа корреляционной структуры рассматриваемого процесса. Модель считается подобранной, если остаточная компонента ряда является случайным процессом, типа белого шума. После подбора модели обычно проводится оценка дисперсии остатков и анализ остатков с целью проверки адекватности модели [2]. Дисперсия остатков принимает участие в формирова- нии доверительных интервалов прогноза, остатки же проверяются на наличие автокорреляции. В случае обнаружения автокорреляции можно сделать вывод о неверной спецификации модели или не были учтены какие-либо важные факторы. Возникновение автокорреляции так же может быть спровоцировано внутренними свойствами ряда, например, регрессионной зависимостью между возмущениями. Исключить данную проблему возможно разными способами, частным решением, для авторегрессионных моделей, может выступить авторегрессионное преобразование, методом скользящих средних, модели ARMA.

В качестве показателей качества (адекватности) построенной модели, может использоваться среднее квадратическое отклонение остатков или среднеквадратиче- также л = ская ошибка: Se = ^^=^—^~, а средняя ошибка аппроксимации:

1 Е ”=1 ^ • 100% [3].

Одной из целей статистического анализа временных рядов является прогнозирование будущих значений рассматриваемого показателя. Прогнозирование будущих значений временного ряда, по сути, осуществляется на основе выявленных закономерностей изменения самого исследуемого показателя во времени, и экстраполяции его прошлого поведения на будущее, предполагая возможность распространения выявленных тенденций на будущий период.

Обычно различают долгосрочное и краткосрочное прогнозирование.

В первом случае анализируется долговременная динамика изучаемого показателя, и в этом случае главным представляется выделение общего направления его изменения – тренда. При этом считается возможным пренебречь краткосрочными колебаниями значений исследуемого показателя относительно этого тренда. Тренд обычно строится методами регрессионного анализа. Рассматривая временной ряд как регрессионную модель с одной объясняющей переменной «время», следует помнить о том, что основные предпосылки регрессионного анализа, касающиеся случайных возмущений, на практике, во многих случаях, бывают нарушены. Стандартные ошибки и доверительные интервалы прогнозов вычисляются точно так же, как и в случае парной линейной регрессии [4].

Для построения краткосрочного прогноза, кроме выделения долгосрочного тренда необходим учет краткосрочных колебаний, например, сезонных. На практике часто пытаются определить дополнительные факторы, вызывающие отклонения значений исследуемой величины от тренда. Кроме этого, проводят более детальное исследование связей текущих значений исследуемых показателей с их прошлыми значениями или с прошлыми значениями других факторов [5].

Следует иметь в виду, что прогнозирование является одной из сложнейших задач анализа, и, в любом случае, подбор подходящей модели требует индивидуального подхода. Удачное использование какой-либо модели для прогноза на некоторый период не является гарантией аналогичного результата для другого периода.

Сезонность

Сезонность относится к периодическим колебаниям. Возьмём, к примеру, потребление электроэнергии: высокое днем и низкое ночью. Или, допустим, онлайн -продажи увеличиваются в период праздников, а затем снова снижаются.

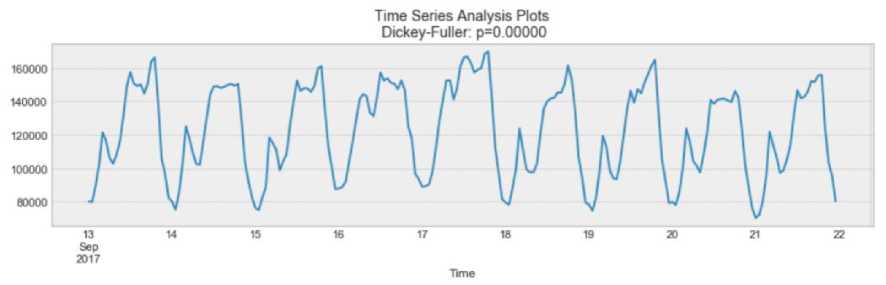
Рис. 1. Пример сезонности временного ряда

Как видно из графика, приведённого на рисунке 1, существует четкая суточная сезонность. Каждый день наблюдается пик нагрузки ближе к вечеру, а самые низкие точки характерны для начала и конца каждого дня. Сезонность также может быть получена из графика автокорреляции, если он имеет синусоидальную форму. Анализ временных рамок периода даёт возможность предположить продолжительность сезона.

Стационарность

Стационарность является важной характеристикой временных рядов. Временной ряд называется стационарным, если его статистические свойства не меняются во времени. Другими словами, оно имеет постоянное среднее значение и дисперсию, а ковариация не зависит от времени.

Идеальным для моделирования является стационарный временной ряд, чего, в некоторых случаях можно достигнуть путём различных преобразований.

Фильтр Калмана

Фильтр Калмана - это рекурсивный фильтр, оценивающий вектор состояния динамической системы, описанной рядом неполных и зашумленных измерений. Название дано в честь Рудольфа Калмана. Однако данный фильтр является частным случаем более общего нелинейного фильтра, разработанного Русланом Леонтьевичем Стратоновичем в конце 1950-ых годов. Фактически же результаты работы советского математика включают в себя некоторые из уравнений для частных случаев линейного фильтра.

Фильтр использует принятую модель генерации авторегрессивного сигнала для получения результатов, которые могут быть существенно скорректированы с помощью анализа каждой новой выборки во временной последовательности. Наиболее пригоден для исследования непрерывного временного ряда, например, в радиолокационных станциях сопровождения.

Алгоритм работает в два этапа: на этапе прогнозирования фильтр Калмана экстраполирует значения переменных состояния, а также их неопределенности. На втором этапе, по данным измерения, полученного с некоторой погрешностью, результат экстраполяции уточняется [6].

Благодаря пошаговой природе алгоритма он может в реальном времени отслеживать состояние объекта без обращения к будущему, используя только текущие замеры и информацию о предыдущем состоянии и его неопределенности.

Экспериментальная часть

Для анализа эффективности применения математических моделей используется программное обеспечение компании по анализу, визуализации и обработке больших данных Splunk. В данной работе используется функционал приложения «Machine Learning Toolkit», а именно инструменты для работы с временными рядами. При анализе тестового набора данных для создания временного ряда будут использованы алгоритмы на основе фильтра Калмана. Фильтр Калмана в Splunk – это инструмент для прогнозирования временных рядов. Прогноз можно создать с помощью команды SPL, не настраивая множества параметров, что упрощает настройку и даёт серьёзный выигрыш в скорости обработки данных, когда требуется быстро провести анализ или отобразить полученные данные.

Фильтр хорош для сглаживания зашумленных временных рядов, но эта простота означает отсутствие гибкости. Используя параметры фильтра затруднительно контролировать и отслеживать множественную сезонность временного ряда, однако, в случае используемого датасета это не требуется. Сезонный прогноз ориентируется на значения последнего наблюдаемого периода, что означает сильную зависимость результатов работы от последних изменений, даже если они принимают значения отличные от наблюдаемых ранее. Для сравнения используется количество значений, которые выбиваются за рамки предсказанных диапазонов, значение среднеквадратичной ошибки, а также коэффициент детерминации.

Для анализа используются наблюдения изменения числа запросов к серверу. Дата-сет содержит значение дельты изменения предыдущего и текущего значений. Для проведения сравнения эффективности методов используется недельный промежуток времени с группировкой значений по часу. Данная группировка позволяет получить плавную кривую изменения числа запросов с чётко отслеживаемой сезонностью. Поэтому на «Hold back» отводится 24 значения, что соответствует последнему периоду. На основе показателей последнего дня строится предсказание значений на следующие 12 часов.

Первым для тестирования используется следующий метод прогнозирования: LL (Local Level) для прогнозирования локального уровня временного ряда. Данный метод не подразумевает определения тенденций или сезонности, на рисунке 2 представлены описанные выше параметры.

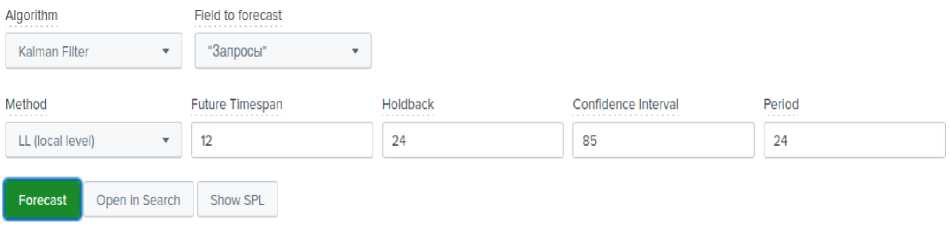
Рис. 2. Параметры для LL метода

На рисунке 3 приведён пример работы   метод игнорирует уменьшение числа за- метода LL. На графике чётко видно, что   просов и строит предсказание будущих значений отталкиваясь от первого значения диапазона «Hold back». Данный метод может дать результат только в том случае, если временной ряд имеет ярко выраженную симметрию изменения значений и возможно подобрать границы набора точек. При мониторинге состояния системы данный метод не может быть использован в силу ограничения гибкости и необходимости калибровки.

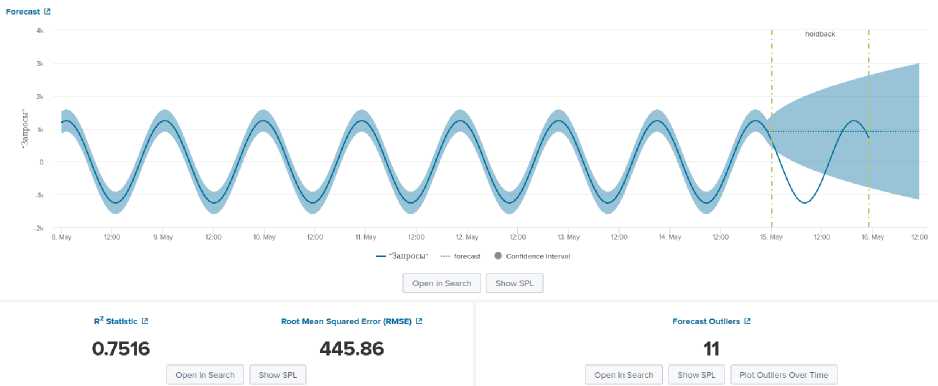
Рис. 3. Результат работы LL метода

Рассмотрим следующий метод: LLT (Local Level Trend) для прогнозирования линии тренда. Для демонстрации функционирования этого метода используются те же значения параметров, что и для метода LL. Конфигурация для метода LLT приведена на рисунке 4.

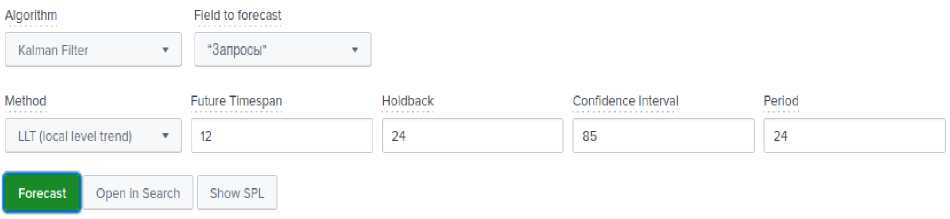
Рис. 4. Параметры для LLT метода

На рисунке 5 приведён пример работы метода LLT. На графике чётко видно, что метод ведёт себя аналогично LL. По критериям можно заметить, что качественных различий не наблюдается. LLT метод явно наследует недостатки ранее описанного метода, на что косвенно указывает число значений не попавших в диапазон предсказанных значений. Коэффициент детер- минации различается на 33 десятитысячных, что показывает незначительное преимущество LLT метода. По значению среднеквадратичной ошибки получается разница 2,96, что является незначительным показателем для данного случая, но тем не менее свидетельствует в пользу LLT метода.

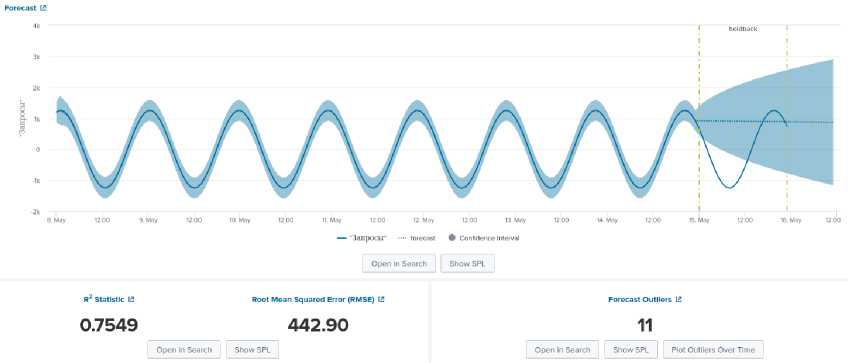
Рис. 5. Результат выполнения для LLT метода

Рассмотрим метод LLP (Seasonal Local Level), может быть использован только для прогнозирования сезонной составля- ющей. Параметры не отличаются от предыдущих опытов и приведены на рисунке 6.

Рис. 6. Параметры для LLP метода

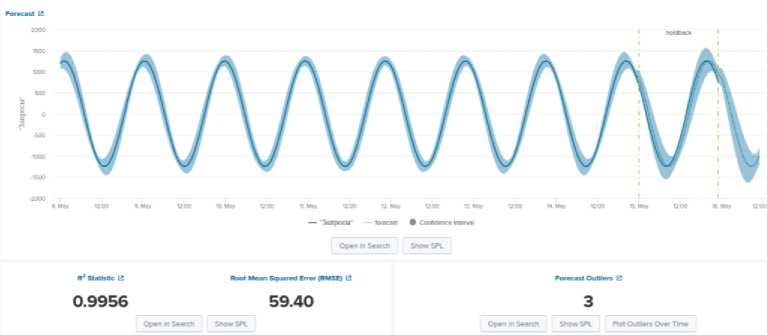
Рис. 7. Результат выполнения для LLP метода

На следующем рисунке 7 приведён результат применения LLP метода, сразу можно отметить, что теперь график максимально приближен к реальным, получаемым значениям и не требует дополнительной калибровки. Если же обратиться к параметрам, характеризующих данную модель, то получается практически идеальный результат: только три точки выби- ваются за предполагаемые границы диапазона изменения значений. Коэффициент детерминации очень близок к единице, что безусловно, положительно характеризует модель, однако при мониторинге в реальном времени точность предсказания может снизиться при возникновении пиковых значений или инцидентов, влекущих трудно прогнозируемые изменения значений.

Резкое уменьшение (по сравнению с предыдущими рассматриваемыми моделями) значения среднеквадратичной ошибки обусловлено тем, что теперь учитывается сезонность изменения поведения системы и прогнозные барьеры повторяют изменения кривой наблюдений.

Последней моделью на основе фильтра Калмана будет LLP5, которая объединяет в себе лучшее от алгоритма LLT и LLP, что позволяет учитывать как значения тренда, так и сезонность данных. Предполагается, что при комбинировании методов модель получается точнее: так как удаётся принять во внимание большее число нестационарных параметров (рис. 8).

Algorithm                         Field to forecast

Рис. 8. Параметры для LLP5 метода

На рисунке 9 представлен результат работы метода LLP5. Как видно из графика, результат не сильно отличается от LLP метода, при этом, сравнение явно не в пользу комбинированного метода. Число значе- ний вне прогнозных барьеров – 7, что хуже результата прогнозирования исключительно с сезонной составляющей. Также увеличилась среднеквадратичная ошибка и коэффициент детерминации.

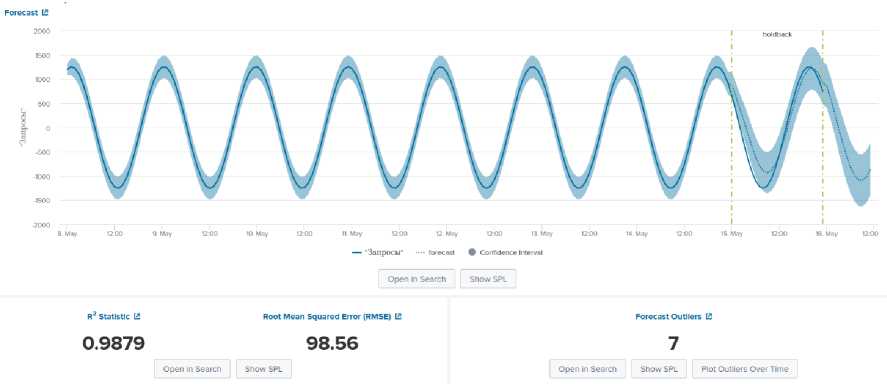
Рис. 9. Результат работы LLP5 метода

Приведённые исследования позволяют сделать вывод, что в использованных данных слабо выражена линия тренда и в явном виде присутствует сезонная компонента. Поэтому, оптимальным методом будет модель LLP5.

Заключение

В данной статье рассматривалось несколько методов анализа и предсказания поведения временных рядов с применением фильтра Калмана. В результате сравнительного анализа было принято решение использовать метод Seasonal Local Level, так как в этом случае были получены наиболее оптимальные критерии оценки модели. Однако, возможно использование модели LLP5 в случаях, когда трендовая компонента более ярко выражена.

В используемом датасете слабо представлена трендовая составляющая нестационарного ряда, что не раскрыло работу метода LLT, однако, при детальном анализе временного ряда он может быть полезен. Использование моделей регрессии удобно при работе с большим количеством статистических данных, для которых не характерны резкие изменения, возможно построить линии тренда и определить сезонность, однако, наиболее оптимальным решением, охватывающим большинство возможных комбинаций составляющих, является LLP5 метод.