Особенности работы вертикальной фурмы в прямоточном режиме

В современной металлургии тяжёлых цветных металлов для переработки концентратов по пирометаллургической технологии преимущественно используются автогенные плавильные агрегаты. Среди относительного разнообразия автогенных технологий и оборудования для реализации процессов переработки существенную долю занимают печи, работающие в режиме продувки расплава через вертикальные фурмы типа TSL с их частичным погружением в расплав [1–9]. Этот способ плавки в вертикальном цилиндрическом реакторе, где топливо, воздух и кислород подаются в печь через вертикальную фурму, реализован в России на единственном предприятии – АО «Карабашмедь» – в 2006 г. [10].

Главной отличительной особенностью фурмы TSL от аналогичного процесса в агрегате автогенной плавки (ААП), внедрённом на комбинате «Североникель» сотрудниками института «Гипроникель» [11] в период 1968– 1970 гг., является закручивание дутьевой струи с целью обеспечения работоспособности неохлаждаемой конструкции фурмы. Степень крутки, характеризующая струйные течения дутьевой смеси, поступающей из фурмы в печное пространство, определяется конструкцией фурмы, особенностями геометрии подсводового пространства печи, уровнем расплава, его физическими свойствами и другими параметрами, рассмотренными далее. Соответственно, управляя параметрами крутки, можно существенно менять основные технологические режимы плавки при переходе от прямоточных к различной степени закрученным дутьевым струям. В то же время часть дутьевых струй, а именно природный газ, поступают в область смешения фурмы в прямоточном режиме, что накладывает существенные особенности на характеристики спутных струй при выходе из её наконечника. В лите- ратурных источниках имеется крайне ограниченный объём информации по теоретическому обоснованию параметров дутьевых струй разной степени крутки для расплавов тяжёлых цветных металлов в условиях плавильных агрегатов типа Аусмелт и Айзасмелт. Как правило, эти данные не раскрываются для широкого круга пользователей при внедрении подобного оборудования. Для оценки влияния дутьевых струй, подаваемых в прямоточном режиме, на вращение ванны расплава и на технологические параметры плавки автором был выполнен анализ теоретических работ в этом направлении, разработана и предложена модель расчёта параметров дутьевого факела при его прямоточном истечении в ванну расплава применительно для условий печей Аусмелт и Айзасмелт.

Виды и особенности дутьевых струй

По классификации Р.Б. Ахмедова струйные течения подразделяются на прямоточные и закрученные [12]. Прямоточные характеризуются двумя составляющими скорости – радиальной и аксиальной. Радиальные скорости в этом случае значительно меньше аксиальных, направленных вдоль струи. Давление в прямоточной струе практически постоянно во всём объёме, за исключением ядра. Основные аэродинамические характеристики прямоточной струи определяются коэффициентом структуры струи, зависящим от формы устья сопла и скоростной неравномерности в устье. Коэффициентом структуры определяются угол раскрытия струи и её дальнобойность, т. е. скорость падения вдоль струи максимальной скорости в сечении. От последнего зависит размер начального и основного участка струи. В соответствии с теорией, разработанной Г.Н. Абрамовичем [13], и выведенными им формулами расчёта струи на основе константы, названной коэффициентом структуры (турбулентности) струи, для цилиндрической трубы он будет равен 0,08, что обеспечивает угол раскрытия прямоточной струи до 30°30' [14].

Закрученная струя характеризуется тремя составляющими скорости – радиальной, аксиальной и тангенциальной, причём около сопла все эти три составляющие могут быть соизмеримы. Радиальная скорость направлена перпендикулярно оси струи, аксиальная – вдоль оси, а тангенциальная – по касательной к окружности вокруг оси струи. В закрученных струях имеется градиент давления как вдоль, так и поперёк струи. В отличие от прямоточных струй, давление во всём объёме закрученной струи ниже давления в окружающей среде.

Угол раскрытия (φ) закрученной струи является несколько условным понятием, так как границы струи у устья сопла образуют не конус, а гиперболоид вращения. Чем меньше разница в плотности закрученного потока и окружающей среды и чем сильнее закручен поток, тем больше форма струи отличается от конической. Из нескольких способов определения границы потока выделим приём, основанный на экстраполяции величины скорости до её нулевых значений. В ряде работ в качестве границы струи принимают 5-, 10- или даже 50-процентную границу [12, 14].

В зависимости от формы сопла в прямоточных струях угол раскрытия наименьший – от 15 до 30° и строго зависит от коэффициента структуры потока. С увеличением коэффициента структуры потока угол раскрытия возрастает, а дальнобойность струи падает.

Угол раскрытия закрученных струй больше, чем в прямоточных, что объясняется тем, что при закручивании потока резко увеличивается массообмен между струёй и окружающей средой. Кроме того, центробежные силы способствуют «разлёту» струи, увеличивая угол раскрытия.

На рис. 1 представлены типы свободных затопленных струй различной степени крутки,

d)

e)

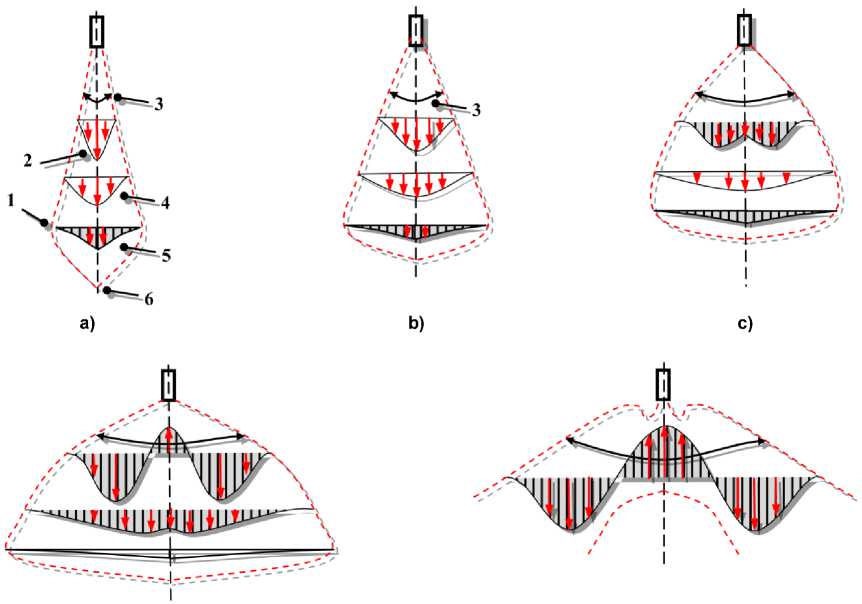
Рис. 1. Профиль скоростей свободных затопленных струй различной степени крутки:

а – прямоточная струя; b – слабо закрученная струя; c – умеренно закрученная струя; d – сильно закрученная сомкнутая струя; e – сильно закрученная разомкнутая струя; 1 – границы струи; 2, 4, 5 – профиль скорости на различных расстояниях от сопла; 3 – угол раскрытия струи ( φ ); 6 – ось струи; стрелками показана величина и направление аксиальной скорости

Fig. 1. Velocity profile of free submerged jets with different degrees of swirl:

a – straight-through jet; b – weakly swirled jet; c – moderately swirled jet; d – strongly swirled closed jet; e – strongly swirled open jet; 1 – jet boundaries; 2, 4, 5 – velocity profile at different distances from the nozzle; 3 – jet opening angle ( φ );

6 – jet axis; arrows indicate the magnitude and direction of the axial velocity

имеющие отличающиеся структуры истечения. Прямоточная струя (рис. 1а) имеет определённый угол раскрытия, который меняется в небольших пределах с изменением коэффициента структуры струи. Слабо закрученная струя (рис. 1b) из-за наличия центробежных сил имеет уже больший угол раскрытия. При этом максимум аксиальной скорости находится на оси струи, как и в прямоточной. Аксиальная скорость имеет в поперечном сечении форму гауссовского распределения. Давление в струе ниже давления в окружающей среде.

С дальнейшим повышением крутки (рис. 1c) профиль аксиальной скорости принимает М-образную форму, максимальная скорость при этом смещается от оси струи. Угол раскрытия струи увеличивается ещё больше. Далее, вниз по течению струи, профиль максимальной скорости вновь смещается к оси струи и его форма снова напоминает свободную прямоточную затопленную струю.

При дальнейшем увеличении крутки (рис. 1d) силы внешнего давления превзойдут аксиальный импульс и вблизи оси образуется обратное течение. Вниз по течению струя снова смыкается. Угол раскрытия сомкнутой струи в этом случае – максимальный.

Увеличение крутки далее (рис. 1e) ведёт к тому, что зона, занятая обратным течением, расширяется настолько, что струя вниз по течению больше не смыкается, а факел приобретает торообразную форму.

Цель исследования

Для анализа работы фурмы в печном пространстве и в зоне расплава необходимо рассматривать взаимодействие спутных струй как закрученных воздушной и кислородовоздушной дутьевых смесей, так и прямоточной струи природного газа. На рис. 2 представлено схематичное изображение вертикальной фурмы TSL, используемой для реализации процесса плавки в печи Аус-мелт. Воздух охлаждения и дутьевая смесь, обогащённая кислородом (КВС), поступают в расплав, предварительно раскручиваясь с помощью лопаточных завихрителей с разной степенью крутки. Природный газ, вдуваемый через центральный канал, не имеет крутки в связи с отсутствием соответствующих устройств для реализации процесса закручивания.

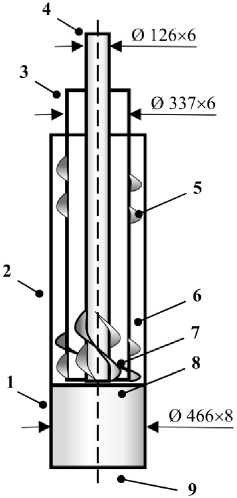
Рис. 2. Изображение рабочей части фурмы печи Аусмелт:

• 1    – наконечник; 2 – наружная воздухоохлаждаемая труба для ввода в расплав воздуха охлаждения; 3 – внутренняя труба для подачи воздуха на технологию в смеси с кислородом (КВС); 4 – труба для вдувания природного газа; 5, 6 – завихрители смеси для воздуха охлаждения; 7 – завихрители для КВС; 8 – устье фурмы;

• 9 – устье наконечника

Fig. 2. Image of the working part of the tuyere of the Ausmelt furnace:

• 1    – tip; 2 – external air-cooled pipe for introducing cooling air into the melt; 3 – internal pipe for supplying air to the technology in a mixture with oxygen (KVS); 4 – pipe for blowing natural gas; 5, 6 – swirlers of the mixture for cooling air;

• 7    – swirlers for KVS; 8 – tuyere mouth; 9 – tip mouth

В то же время на примере агрегатов автогенной плавки, разработанных на комбинате «Североникель», при организации автогенного процесса возможно использование дутьевой смеси, исходящей из вертикальной фурмы в расплав в условиях истечения прямоточных или слабо закрученных струй.

С целью сопоставления и сравнения разных режимов работы дутьевых фурм для продувки расплавов тяжёлых цветных металлов предложена методика расчёта вертикальных фурм, несколько отличающаяся от общепринятых схем в стационарных плавильных агрегатах, имеющих большую площадь сечения и объёмы плавильной зоны [15, 16]. В рамках настоящей статьи автор рассмотрел параметры и представил для обсуждения методику расчёта вертикальной фурмы с прямоточной дутьевой струёй для условий печей Аусмелт и Айзасмелт, имеющих небольшой объём продуваемого расплава в ограниченном плавильном пространстве вертикальной печи.

Существующая методика расчёта прямоточных дутьевых струйдля глубоких ванн с большой поверхностью

В СССР и РФ основными исследователями и теоретиками продувки расплавов цветных металлов (сульфидов меди, никеля и свинца, а также шлаков) являлись А.В. Гречко, Л.М. Шалыгин, А.А. Гальнбек и др. [5–7, 15, 17].

В соответствии с выводами в работе [17] Л.М. Шалыгина представим основные положения по продувке медно-никелевого расплава в печи Аусмелт с использованием вертикальной фурмы (рис. 3).

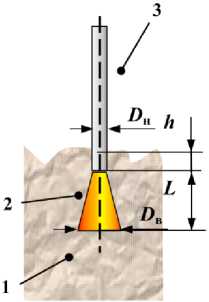
Рис. 3. Схема вертикальной фурмы:

• 1    – расплав; 2 – дутьевой факел; 3 – фурма; D _в – диаметр воронки; D н – диаметр наконечника; h – глубина погружения в расплав наконечника; L – длина факела

Fig. 3. Schematic diagram of a vertical tuyere:

• 1 – melt; 2 – blast torch; 3 – tuyere; D _в – funnel diameter; D н – tip diameter; h – tip immersion depth into the melt;

L – torch length

Для типового и стабильного режима плавки в печи с использованием вертикальной фурмы, не оснащённой специальными завихрителями, давление кислородовоздушной смеси (КВС) на выходе из наконечника изменяется от 0,6 до 0,7 кг/см2. Для дальнейших расчётов примем давление в наконечнике равным 0,6 кг/см2 или 0,6·104 кг/м2. Для упрощения анализа и большей наглядности расчётов давление в подсводовом пространстве печи условно примем равным нулю, по факту – 40 Па или 4 кг/м2, что может вносить минимальную погрешность в анализе.

При глубине погружения фурмы в оксидосульфидный расплав тяжёлых цветных металлов плотностью 3500 кг/м³ на h = 0,3 м создаётся противодавление, равное 0,3 · 3500 = 1050 кг/м².

Отношение абсолютного давления в наконечнике к противодавлению расплава равно (6000 + 10 000)/(1050 + 10 000) = 1,45, что меньше критерия 1,9, характеризующего переход от докритического режима истечения к сверхкритическому. Критическое давление истечения при погружении наконечника в расплав на 0,3 м будет равно: 1,9 · (1050 + 10 000) = 20 995 кг/м2 или 2,1 кг/см2 или 1,1 ати.

В соответствии с исследованиями Л.М. Шалыгина, для расплавов тяжёлых цветных металлов можно применять основные выведенные им формулы для расчёта дутьевых характеристик фурмы, соответствующие докритическому истечению дутья в расплав для прямоточной и незакру-ченной струи.

Теоретический удельный расход воздушной дутьевой смеси через наконечник фурмы равен

Гуд = 34,8 •ФР, • W-» ДТ^                              (1)

где 1 уд — удельный расход воздушной смеси, м³/(см²^мин);

Ф – коэффициент диафрагмирования, учитывающий изменение сечения наконечника по сравнению с первоначальным значением, доли ед.;

Р _г - абсолютное давление истечения смеси в расплав, кг/м²;

P_h - абсолютное противодавление слоя расплава на глубине h, кг/м²;

Т - абсолютная температура дутьевой смеси, К;

к - показатель адиабаты, равный для воздуха и кислорода 1,4;

Y - приведённый удельный вес газа, кг/нм3.

Для определения фактического расхода дутья через наконечник необходимо по результатам экспериментов или практической работы фурмы определиться с коэффициентом Ф.

Теоретическая скорость дутья из наконечника фурмы равна

*                               м/с,                                               (2)

где W_a - скорость газа на выходе из наконечника фурмы, м/с;

Ф - коэффициент, учитывающий потери энергии на преодоление сопротивления воздухоподводящей системы;

Р_о - нормальное давление, кг/м²;

Н - абсолютное гидростатическое давление слоя расплава, кг/м²;

Т_о - абсолютная температура, К.

Фактическая скорость истечения будет определяться с использованием коэффициента ф.

Методика расчёта прямоточного дутьевого режима для условий плавкив печах Аусмелт и Айзасмелт

Опираясь на расчёты Л.М. Шалыгина, выведем основные зависимости для расчёта вертикальной фурмы для прямоточного режима на воздушном дутье с использованием методик, разработанных Ю.А. Королём и С.С. Набойченко, и представленной в работах [18, 19].

Расчёт для прямоточного истечения природного газа будет представлен в рамках расчёта взаимодействия спутных струй закрученного потока.

Пропускная способность фурмы

Определим теоретическую пропускную способность фурмы в зависимости от давления дутья и температуры воздуха. Преобразуем уравнение Бернулли – Сен Венана относительно воздуха в указанной последовательности и получим первое расчётное уравнение для определения теорети-

_                                  k Рф   k H ®2              _ ческой пропускной способности фурмы Vф:---- =----1--. Для рассматриваемых

k -1 рф k -1 р 2

условий изоэнтропического процесса можно записать соотношение:

Р рф

^ Н У k

У Рф 7

^ H ^ k

, р = рф • P

У Рф 7

,

где р - плотность газа в факеле, кг/м3. Отсюда скорость истечения воздуха из фурмы будет равна

ю =

2 k P ф — k ^{- 1 р} ф

1 -

r H

k - 1 у k

Р, у ^ф 7

, м/с,

где Р ф – давление дутьевой смеси в фурме, кг/м²;

ρ ф – плотность смеси в фурме, кг/м³;

Н – противодавление слоя расплава, кг/м²;

k – показатель адиабаты, равный для воздуха и кислорода 1,4.

В соответствии с уравнением Клайперона – Менделеева покажем следующее соотношение

Pф давления и плотности газа: — = R • T. Соответственно, масса дутья Сн, проходящего через сече-рф ние наконечника Рн, будет равна Сн = р ■ ю • /н = рф получим формулу для определения массы дутья:

\^^{к з й}У

Сн=рн■^■^■[И"И ], кг/с.

•

■ ю ■ Рн. Преобразуя эту зависимость,

Видоизменяя данную формулу в расход воздуха в м³/мин для воздуха, при k , равном 1,4, имеющего R – 287,14 Па·м³/(кг·К) и плотность – 1,29 кг/нм³ с указанием давления смеси в кПа, получим

158,7          з I 1     Г7Й\^ ThY’^4 ₃

* =^^FH   _^v 8-i_;.< I -U)   [ м/мин,                   ⁽⁵⁾

где Р ф - абсолютное давление дутьевой смеси в фурме, кПа;

1,29 – плотность воздуха в фурме, кг/м3;

Н - абсолютное противодавление слоя расплава (0,3^3500^0,00981 + 101,3), кПа;

Т - температура дутьевой смеси, К.

Р_н - свободное сечение наконечника, м 2 .

Представленные формулы характеризуют дутьевые параметры прямоточного дутья для воздушной смеси. Для кислородовоздушной смеси, содержащей 60 % кислорода, плотность дутьевой смеси будет равна 1,361 кг/м3 (см. таблицу), в этом случае формула (5) теоретического расхода дутья будет иметь вид:

158,7               И    Г/«З1,425 (НЗ1'715! 3.

'   _; ,./ ⁴ •Р ф <^O^ .:/J J —У    ], ^м/мин,                        ⁽⁶⁾

где 270 – универсальная газовая постоянная для смеси КВС, содержащей 60 % кислорода:

8314/(29·0,4 + 32·0,6) = 270 Дж/(кг·К).

Плотность обогащённого воздуха кислородом [20] Density of oxygen-enriched air [20]

O 2 , % об.	Воздух, % об.	Содержание кислорода, % об.	Плотность, кг/м3
0	100	21,00	1,293
20	80	36,80	1,320
30	70	44,70	1,334
40	60	52,60	1,347
50	50	60,50	1,361
52	48	62,08	1,364
54	46	63,66	1,366
56	44	65,24	1,369
58	42	66,82	1,372
60	40	68,40	1,375
70	30	76,30	1,388
80	20	84,20	1,402
90	10	92,10	1,415
100	0	100,00	1,429

Расчёт для воздушного дутья при прямоточной струе показывает, что теоретическая пропускная способность наконечника диаметром 0,45 м для температуры 250 °С составляет 1993 м3/мин или 119 570 м3/ч. Для КВС, содержащей 60 % кислорода, теоретическая пропускная способность наконечника диаметром 0,45 м составит 1948 м3/мин или 116 888 м3/ч.

Фактическая максимальная пропускная способность фурмы по воздушному дутью на АО «Кара-башмедь» находится на уровне 60 тыс. нм3/ч, соответственно, можно предположить, что смесь КВС нагревается в фурме, охлаждая её до уровня не выше 250 °С. По факту расход воздушной смеси через фурму равен 60∙(273 + 250)/273 = 115 тыс. м3/ч, что сопоставимо с расчётным количеством – 117 тыс. м3/ч.

Расчёт давления дутья на срезе фурмы

Продолжая расчёт параметров прямоточной струи для фурмы печи Аусмелт, определим давление воздушной смеси на выходе из наконечника в расплав путём преобразования давления в фурме и уравнения неразрывности потока:

“ = ДЙЙЙ’ м/с,                        (7)

где Р_т - давление дутьевой смеси на срезе наконечника, кг/м²;

Н - противодавление слоя расплава, кг/м²;

к. - показатель адиабаты, равный для воздуха и кислорода 1,4.

Давление воздуха в фурме равно давлению торможения смеси на выходе из наконечника Р т и сопротивлению трения внутри фурмы Р _тр:

Р ф = Р т + Р тр , кПа.                                                                       (8)

Для оценочного расчёта потери давления на трение в трубе фурмы примем его по внутренней трубе для подачи основной доли кислородовоздушной смеси, отсюда

^Р т ^р = ^Х ^ ^ Р _Ср ^   ^^{10 -3} ’ кПа,                                                            (9)

где λ – коэффициент трения, являющийся функцией критерия Рейнольдса, равный для стальной трубы 0,04;

Ь ф - длина фурмы - 18,6 м;

^вн - внутренний диаметр внутренней трубы фурмы для смеси КВС - 0,306 м;

р _{с р} - средняя плотность смеси в канале фурмы, кг/см²;

ω ср – средняя скорость смеси в фурме, м/с.

Среднюю плотность смеси в канале фурмы рассчитаем по формуле

Р ср = Р о‘^ кг/м³,                                                            (10)

где р _о , Т_о и Р_о - плотность, температура и давление воздуха при н. у., кг/м³, К, кПа соответственно, 1,361 для смеси КВС (60 % об. кислорода), 273 К и 101,3 кПа;

Т – температура воздуха на срезе фурмы, 250 + 273 = 523, К;

Р ср - среднее давление воздуха в канале фурмы, равное ( P ф + P _т)/2, кПа.

Из уравнения неразрывности потока находим среднюю скорость воздуха в канале фурмы:

®cn = V° Р°, м/с,(11)

ср Рср • где Рг - площадь сечения наконечника, 0,16 м2.

Преобразуя указанные уравнения относительно P _т и при Р ₀, соответствующем 101,3 кПа, Т 0 – 273 К, получим формулу для смеси КВС:

Рт = )Рф2-3,7-10-4 ■ X-^Р-°°^-Т, кПа, N                           ^вн

129,7 кПа.

где V ф – теоретический расход КВС на фурму, м³/с.

I Э                         186 1,361 Zi2^)2- 523

Отсюда Р_т =

161,32 - 3,7 ■ 10-4 ■ 0,04 ■ —--^°^

J                               0,3060,07

В соответствии с выполненным расчётом относительное давление торможения на срезе наконечника для прямоточной струи находится на уровне: 129,7 – 101,3 = 28,4 кПа.

Скорость истечения дутья

Для определения скорости истечения дутьевой смеси из наконечника фурмы, содержащей 60 % кислорода, воспользуемся формулой, где универсальная газовая постоянная для КВС равна 270 Па·м3/(кг·К):

“ = ДЙЙЙ = ^7^:270^(250^²74-( ¹ 2£’⁵]'= 203,8 м/с.

Отметим, что полученная скорость истечения КВС для рассматриваемой фурмы меньше критической скорости 402 м/с:

w_Kp = 20,5 • / Т = 20,5 • 1 ^{250 + 273} = 402 м/с.

кр , ^P o         ,         1,361               ¹

Глубина погружения струи в расплав

Для определения глубины погружения прямоточных струй в расплав рассчитаем критерий Архимеда по методике И.Г. Казанцева [15, 17]:

Ar =

m2 • Рг

3 ^ррасп ^

где Ar – критерий Архимеда;

ω – скорость истечения струи в расплав, 203,8 м/с;

ρг – плотность газа на выходе из наконечника на глубине 0,3 м, кг/м3;

ρрасп – плотность расплава, кг/м3;

d - диаметр наконечника, м.

1                                                  1

P = P • Z ° • ^ •     = 1,361 • ^ • ^ • (m^U = 0,82 кг/м ³ .

^{r г    r0} T ₁ P ₀ PpJ              523 101,3 \129,7/               '

Соответственно, критерий Архимеда будет равен

Ar = ²⁰³^² - ⁰ ,8 ² = 2,2.

9,81-3500-0,45

Для определения глубины погружения струи дутья в расплав L при прямоточном истечении воспользуемся формулой, выведенной Л.М. Шалыгиным для вертикальной струи:

L = 2 • Ar • [1 - 0,95 •( ;! •tan -¹ (£))], м.                                                 (14)

Отсюда при диаметре наконечника d = 0,45 м глубина погружения прямоточной струи в расплав будет равна 0,96 калибра или 0,4 м.

При угле раскрытия струи, характерном для прямоточных струй 23°, диаметр образующейся воронки можно определить по формуле

DB = d + 0,4 • %, где х – расстояние от наконечника фурмы, м.

Для расстояний от устья наконечника до 1,0 м, диаметр воронки прямоточной струи будет изменяться следующим образом:

Расстояние, м

Диаметр воронки, м

0,2       0,4       0,6       0,8       1,0

0,39     0,47     0,55     0,63      0,7

Аналогичный результат по глубине погружения прямоточной струи в расплав, равной 1,04 калибра или 0,7 м, даёт и другая уточнённая формула Л.М. Шалыгина [17]:

_I= 2 •^Ar•^[1-O^5•(l•tan ^-■ (^ ^ )⁾], м.

Зоны циркуляции и модель движения расплава и газовых потоков в печи

В соответствии с выполненными расчётами для прямоточной дутьевой струи по определению предельных значений объёмов дутьевых потоков (117 тыс. м3/ч), их температуры (250 °С), противодавления на выходе из фурмы (28,4 кПа), скорости смеси (203,8 м/с), диаметра (от 0,4 до 0,7 м) и глубины проникновения воронки в расплав (0,4 м) для условий вертикальной печи далее сделаем предположение о вероятном движении расплава и газовых потоков при реализации процесса в печах Аусмелт и Айзасмелт.

При этом отметим ряд характерных отличий, присущих рассматриваемым конструкциям печей, а именно:

• –    ограниченная по диаметру цилиндрическая зона плавления;

• –    центральное расположение дутьевой фурмы;

• –    боковая односторонняя загрузка шихты на расплав;

• –    большая зона свободного падения шихты в атмосфере печи;

• –    боковой вывод расплава через сифон, находящийся на сопоставимом уровне с наконечником фурмы;

• –    относительно однородный расплав во всём внутреннем горне печи, без расслоения его на штейновую и шлаковую зоны;

• –    движение газового потока против падающего потока шихты;

• –    несимметричность циркуляционных потоков как для дутьевой смеси, так и для расплава;

• –    видимое вращение расплава за счёт непрерывного вывода его через сифон из внутренней ванны печи и колебаний наконечника фурмы;

• –    односторонний вывод отходящих газов через аптейк в своде печи.

Конструктивные особенности печи приводят к тому, что при прямоточной струе движение расплава во внутреннем горне можно разделить на три неравные циркуляционные зоны (рис. 4).

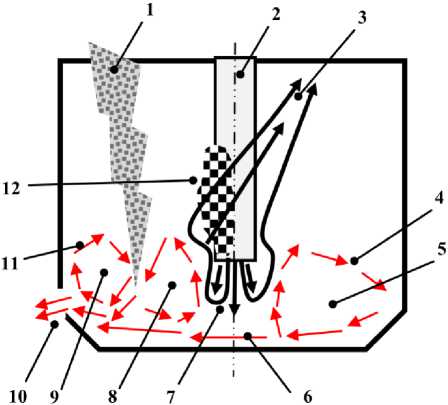
Рис. 4. Схематическое изображение потоков шихты, газа и расплава в печи Аусмелт при прямоточной дутьевой струе:

1 – загрузка шихты; 2 – вертикальная фурма; 3 – отходящий поток газов; 4 – третья зона циркуляции расплава; 5 – зона застоя; 6 – движение расплава в сторону сифона; 7 – дутьевая воронка; 8 – вторая зона циркуляции расплава; 9 – зона застоя первой области циркуляции расплава; 10 – выход расплава из печи через сифон; 11 – первая зона циркуляции расплава в зоне загрузки шихты

Fig. 4. Schematic representation of the flows of charge, gas and melt in the Ausmelt furnace with a direct-flow blast jet:

1 – charge loading; 2 – vertical tuyere; 3 – outgoing gas flow; 4 – third zone of melt circulation; 5 – stagnation zone; 6 – movement of melt towards the siphon; 7 – blast funnel; 8 – second zone of melt circulation; 9 – stagnation zone of the first region of melt circulation; 10 – melt exit from the furnace through the siphon; 11 – first zone of melt circulation in the charge loading zone

Первая и вторая зоны находятся в области загрузки шихты на расплав, где капли расплавленных сульфидов и окисленных компонентов шихты погружаются в расплав, имея больший удельный вес, и под действием потока расплава выводятся из зоны дутьевого факела фурмы продуктами окисления и кислородом дутья. Нисходящий поток расплава делится на две части, одна из которых частично участвует в восходящей циркуляции расплава вдоль стенки печи и частично перетекает в сифон выпуска расплава. Другая часть формирует восходящий поток вдоль дутьевой воронки, вторично попадая в зону загрузки шихты. Этот сульфидный расплав затягивается в дутьевую область факела, где активно взаимодействует с кислородом дутья, дегазируется с выделением диоксида серы, вспениваясь, теряет свой удельный вес за счёт насыщения газом и всплывает под действием сил Архимеда и дутьевых струй факела. Обе эти зоны имеют условные области застоя с минимальным перемешиванием и массообме-ном расплава с компонентами шихты и кислородом дутья (рис. 4, поз. 8, 9).

Поток расплава, движущийся через отверстие сифона в печи (рис. 4, поз. 10), имеет небольшое вращательное движение, передающееся на всю массу расплава, создавая его видимое вращение. Условия для придания расплаву вращения возникают из-за вибраций наконечника фурмы при пульсациях дутья, продуцирующих дутьевые вихри, неперпендикулярные поверхности расплава и создающие эффект его постепенного раскручивания перпендикулярно оси фурмы, а также боковой воронкообразный выпуск расплава.

Третья циркуляционная зона (рис. 4, поз. 4) находится в противоположной от загрузки и выпуска расплава части печи, характеризуется невысокой скоростью циркуляции расплава под действием восходящих газовых струй и вспенивания расплава при его насыщении газами в дутьевой зоне. Часть расплава этой зоны повторно засасывается в дутьевой факел и участвует во вторичной стадии окисления и ошлакования, повышая тем самым свой удельный вес, что способствует выводу расплава из этой зоны циркуляции по подине печи в сторону сифона (рис. 4, поз. 6).

Для этой зоны характерна большая область застоя с пониженным массообменом компонентов шихты, расплава и кислорода дутья (рис. 4, поз. 5). Кроме того, в этой части в первую очередь возникают предпосылки для переокисления расплава и образования магнетита, способствующего массовому вспениванию расплава и выбросу его из печи.

Отсутствие возможности значимой подачи шихты в эту область печи требует от персонала строгого контроля за соотношением железа, серы в шихте и кислорода дутья, за количеством подаваемой смеси КВС и уровнем заглубления наконечника фурмы в расплав, что, в конечном итоге, ограничивает производительность печи по перерабатываемой шихте.

Для снятия этой проблемы возможны два пути: организация загрузки шихты как минимум из двух, противоположных относительно фурмы, течек или обеспечение циркуляции расплава, выравнивающего неравномерное распределение шихты во внутреннем горне печи; обеспечение вращения ванны для улучшения массообмена.

Разработчики процесса TSL пошли по второму пути, предложив закручивание дутьевого факела, что приводит к крутке расплава, увеличению массо- и теплообмена в печи, способствует выравниванию распределения сульфидов и флюсов по всему объёму ванны.

Кроме того, эффект закручивания дутья позволил повысить эффективность конвективного теплообмена в фурме и, соответственно, охлаждения её поверхности, что, в свою очередь, дало возможность опустить наконечник фурмы в расплав, усиливая процессы перемешивания во внутреннем горне печи.

Отличительной особенностью прямоточной струи из вертикальной фурмы при погружении её в расплав является наличие почти сплошных и непрерывных газовых полостей вдоль поверхности наконечника фурмы, соединяющих дутьевой факел с атмосферой печи. Это обстоятельство приводит к снижению противодавления истечению дутья в расплав, но одновременно уменьшает массообмен в объёме ванны, часть кинетической энергии струи выводится из зоны контакта вверх, попутно увлекая капли расплава в подсводовое пространство печи, повышая брызгоунос.

Масса расплава, увлекаемая вверх вдоль фурмы образующимися газовыми струями, движется под углом к оси фурмы из-за небольшого вращения ванны, а соответственно, и газового потока, усиливаемого боковым отводом газа из печи (рис. 4, поз. 3), что в итоге приводит к налипанию массы на поверхность наружной трубы фурмы и образованию одностороннего гарнисажа на ней (рис. 4, поз. 12). Объём гарнисажа и его долговечность определяются химическим составом шлака, температурой в печи и теплосъёмом внутри фурмы, потоком охлаждающего воздуха. В рассматриваемом случае основная доля гарнисажа образуется на одной из сторон фурмы, что приводит к нарушению её балансировки, сложностям управления и искривлению по оси фурмы, в конечном итоге требующим остановки плавки и очистке фурмы от настыли.

Заключение

В представленной статье показаны особенности работы вертикальных фурм при продувке расплавов тяжёлых цветных металлов в процессах автогенной плавки с использованием фурм, обеспечивающих различную степень крутки дутьевого факела. Для условий прямоточного дутья предложена математическая модель расчёта параметров фурмы, обеспечивающих получение данных о предельных количествах воздушной смеси, подаваемой в расплав, её скорости истечения и величины противодавления расплава воздушному потоку, диаметре воронки и глубине погружения дутья в расплав. Все эти параметры позволяют управлять процессом плавки, обеспечивая её максимальную эффективность. Кроме этого, представленная модель расчёта параметров дутья позволяет выполнить прогноз и оценку зон циркуляции расплавов в печи, выделяя участки, влияющие на её стабильную работу, предотвращая вспенивание ванны расплава путём реализации как технологических приёмов плавки, так и внесением определённых управляющих воздействий на массо- и теплообмен в ванне печи.