Особенности расчётов полей давлений в камерах электроимпульсной установки

Экспериментальные исследования [4] позволили впервые выявить существование для ЭПНВ неравномерного поля давлений на преграде при осесимметричном расположении изолированного электрода в разрядной камере. Было установлено, что разрядный канал, например, образуется в одном радиальном направлении между центральным изолированным электродом и стержнем-тоководом, а максимальное давление возникает на преграде не под импульсным источником, а в противоположном радиальном направлении. На основе полученных экспериментов в [4] была представлена разработанная эмпирическая модель, не позволяющая объяснить выявленные эффекты. Однако значительный интерес представляют численные расчёты на основе разработанной математической модели, позволяющие представлять особенности физической картины исследуемых процессов, как в [4]. В связи с этим в данной статье изложена математическая модель для исследования нестационарных и неодномерных процессов в жидкости, возникающих при высоковольтном электрическом разряде.

Постановка задачи. Схема для моделирования нестационарных и неодномерных процессов в жидкости при электроразряде, представлена на рис.1, причём за основу принята одна из камер ЭИУ. Для определения гидродинамического поля внутри камеры с двумя электродами Г 7 и Г 8 , погруженными в жидкость (см. рис. 1), необходимо найти решение краевой задачи.

Верхняя часть камеры представляет собой купол в виде полусферической поверхности Г4, соприкасающейся по диаметральной плоскости с цилиндрической частью камеры Г3 с радиусом re, причем граница Г2 является плоской поверхностью в нижней части цилиндрической камеры Г3. Цилиндрическая поверхность Г5 – это боковая поверхность диэлектрика, в котором размещен центральный электрод Г7. Граница Г6 – это плоская поверхность цилиндрического диэлектрика. Стержень-токовод Г8 размещен на границе полусфера-цилиндр, т.е. между жесткими поверхностями Г4 и Г3. После пробоя межэлектродного промежутка Г7 и Г8 в жидкости образуется разрядный канал с высоким давлением в виде некоторого импульсного источника Be(t).

4+4+4=0.

9x   Уу   9z2

На границах электродов с учётом зарядов записывается уравнение Пуассона в виде:

9 ² q a ² q a p q

9x²   Уу ²    9z²      cC r ’

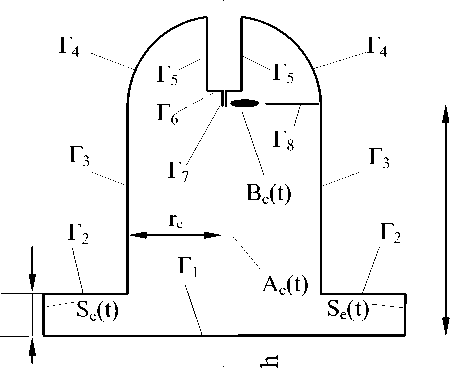
Рис. 1. Схема моделирования разрядной камеры: A_e(t) – область жидкости; B_e(t) – импульсный источник; Г 1 ...Г 6 – жесткие границы; Г 7 – центральный изолированный электрод; Г₈ –стержень-токовод, связанный с корпусом камеры; S e (t) – граница симметрии; r e – радиус разрядной камеры; l – дистанция между B_e(t) и дном камеры (граница Г 1 ); h – расстояние между границей Г 2 и дном камеры Г₁

где ρ q – объёмная плотность зарядов; ξ 0 – электрическая постоянная; ξ r – относительная диэлектрическая проницаемость жидкости.

Для представления параметров исследуемого процесса в безразмерных величинах, исходя из закона подобия и размерности, а также выбрав за базовые величины разность потенциалов между электродами u=ξ 1 -ξ 2 , характерный размер разрядной камеры в поперечном направлении r =r e и величину c 1 = ρ q /( ξ 0 ξ r ) запишем их в следующем виде:

, * c * x * у * z q = -; x = -; у = -; z = -;

u       r        r       r

c * =p q /( C o С r )(1/ C 1 ).

С учётом безразмерных величин уравнение Лапласа будет иметь вид

A ^’ = 0,

Для упрощения исследования основных процессов при электроразряде в жидкости представим данную задачу в виде 2-х этапов, как в [5], каждый из которых будет описываться на основе некоторых систем уравнений, максимально упрощённых в соответствии с особенностями рассматриваемого отрезка времени. При этом решение задачи, полученное на 1-ом этапе, будет служить исходной информацией для численных расчётов на 2-ом этапе.

Первый этап. На первом этапе определяется граница канала пробоя в жидкости после подключения специальным коммутирующим устройством высоковольтного напряжения к электродам Г 7 и Г 8 . Исходные параметры жидкости на этом этапе не изменяются, т.е. скорость частиц жидкости U в начале t н и в конце t к этапа равна нулю: t н = t к = t 0 , U =0. Определение границы канала пробоя в жидкости связано с расчётом поля электрического потенциала ξ в области A(t 0 ). Для расчёта поля ξ используется уравнение Лапласа, в декартовой систем координат имеющее вид

где Δ – оператор Лапласа.

Аналогично    уравнение    Пуассона:

A ^* =- с * . Граничные условия для схемы модели (см. рис. 1) следующие:

– на границе Г 7 : ξ^*=const;

– на Г 1 , …, Г 4 , Г 8 : ξ^*=0;

- на Г 5 , Г б и на S e (t o ): ^^ = 0 .

оn

Учитывая, что напряжённость электрического поля определяется через градиент потенциала, то в безразмерном виде компоненты напряжённости электрического поля следующие:

E x =

—

dq *

9x * ;

Е У

—

dq *

;

9у * ;

E z

—

dC *

;

6Z *

.

Зная компоненты напряжённости E x^* , E y^* , E z^* , можно определить модуль E i^* в любой точке области A e (t 0 ):

E * =V ( E x ) ’ + ( E * ) ’ + ( E Z ) 2 .

Определив поле E i^* в области A e (t 0 ), находим границу канала пробоя в жидкости между электродами Г 7 и Г 8 как линию с максимальными значениями E i^* в виде границы B е (t 0 ). При этом значение напряжённости поля вдоль силовой линии определяем как

E _: 1 vBl c   m^S Id n

Первый этап заканчивается определением границы B e (t o ).

Второй этап. На этом этапе исследуются волновые процессы в жидкости по аналогии с [6] при известном расположении импульсного источника Be(t). Из линеаризованных уравнений гидродинамики следует волновое уравнение, которое относительно потенциала скорости ψ имеет вид д2у д2у д2у _ 1 д2v дx2    ду2    дz2    a 2 д t2 ’

где а о - скорость звука в жидкости.

Учитывая, что в области жидкости Ae(t) имеется импульсный источник Be(t), то на границе канала пробоя в жидкости необходимо использовать неоднородное волновое уравнение

Ау -

1 д ² у a ₀² д t^г

= f ( t )’

где ft ) - потенциальная функция, учитывающая изменение давления в источнике B_e(t).

Зная распределение потенциала ψ в области A e (t), можно определить основные параметры исследуемого процесса при высоковольтном разряде в жидкости. Давление в жидкости определяется из интеграла Коши-Лагранжа, который приводится к виду

—

P i

: P

ду ро "^Г’ д t

где P ₀, р₀ - соответственно давление и плотность покоящейся жидкости.

Плотность связана с потенциалом ψ следующей зависимостью:

Р^:Р о

Р о ду a 2 д i t

Скорости частиц жидкости определяются через градиент потенциала у:

U

x

5*. тт --⁵ У. и ду

’ Uy     а.,’ Uz дx         дУ         дz

.

Граничные условия на этом этапе следующие:

- на жёстких границах Г 1 , .„, Г₆ и на S_e(t): 5*: 0’ д n

Здесь Pm - максимальное давление в Be(t); p0 -плотность жидкости; т - постоянный коэффициент, характеризующий процесс изменения Р(t) в Be(t); электроды (Г7, Г8) не влияют на волновые процессы и не учитываются. Начальные условия при t = t0 нулевые. На этом этапе за базовые величины были выбраны т, Pm,, т.е. т, Pm - параметры импульсного источника Be(t). Безразмер-F ные параметры определялись как F = -7, где F б-Fб базовая величина.

Результаты вычислений. Для решения краевой задачи применён метод конечных разностей [7]. Область жидкости представляется в виде дискретной (сеточной) области. В основу положена замена уравнений в частных производных для рассматриваемых краевых задач на 2-х этапах расчётов их разностными аналогами. В расчётах реализуется явная разностная схема [7] для уравнений (6) и (7). Для уравнений Лапласа и Пуассона реализуется неявная разностная схема с использованием для их решения метода Либмана с ускоряющим множителем для оптимизации итерационного процесса [8]. Для решения исходных уравнений (6) и (7) в декартовой системе координат значение шага A t определялось из обобщённого условия Куранта [9] и затем уточнялось при численных расчётах. Для неявной схемы решения уравнений Лапласа и Пуассона характерна безусловная устойчивость.

Вычислив место расположения импульсного источника B e (t 0 ), образовавшегося в результат пробоя разрядного промежутка, а также учитывая характер изменения в нём давления P ( t ) по колоколообразному закону [10], можно с помощью численных расчётов на базе методики 2-го этапа для краевой задачи определить гидродинамические поля давлений в исследуемой разрядной камере. Следует отметить, что при детонации горючей газовой смеси в цилиндрической камере, частично заглублённой в жидкость [6], время фронта нарастания давления от расширяющихся продуктов детонации составляет величину (100_400)*1O^-6 с, тогда как при электроразряде в жидкости фронт нарастания P ( t ) как минимум на порядок меньше. Исходя из обобщённых экспериментальных данных, величина параметра т для B e (t) принималась равной 10*10^-6 с.

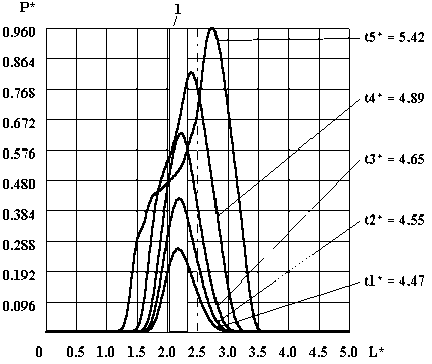
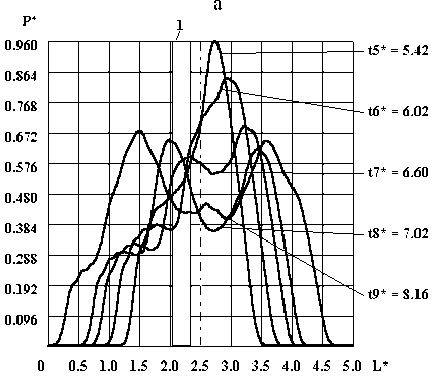
Результаты вычислительных экспериментов для плоской модели исследуемой камеры (рис. 1) показаны на рис. 2. Следует отметить, что на рис. 2 приведено характерное распределение давления P_1n по поверхности Г 1 для моментов времени t i , причём на рис. 2 а показан процесс нарастания давления до максимальной величины P max , а на рис. 2 б - процесс уменьшения давления от P max^* до его некоторого значения.

б

Рис. 2. Эпюры давлений на дне камеры, рассчитанные по явной схеме для плоской модели: а – процесс нарастания давления; б – процесс уменьшения давления; 1 – расположение B_e(t) относительно оси камеры

При этом следует отметить, что длина границы Г 1 (см. рис. 1) в расчёте принималась L = 5 r , расстояние от электродов до границы Г 1 равно 0,5 r , а высота цилиндрической части камеры равна 1,175 r. Анализ результатов численных расчётов (см. рис. 2) показал, что при смещении влево разрядного промежутка относительно оси разрядной камеры путём размещение Г 8 слева, приводит к возникновению канала пробоя данного разрядного промежутка и появлению импульсного источника B е (t) слева. Тогда максимальная величина давления P max^* на преграде наблюдается внизу, но смещается вправо по отношению к оси разрядной камеры. Наблюдается случай, при котором максимальное значение P max^* не расположено непосредственно под источником B е (t), как следовало бы этого ожидать.

Аналогичные результаты численных расчётов приведены на рис. 3 для объёмной модели исследуемой камеры. Для объемной и плоской моделей плоскость их сечений проходит в каждом случае через источник B e (t). При этом на рис. 3 приведено характерное распределение временных характеристик в виде изменения P ^*( t )

на преграде для объемной модели с учётом того, что на рис. 3 а показан процесс нарастания давления до P max для определенных моментов времени t ^*i , а на рис. 3 б показан процесс уменьшения давления во времени t ^* i .

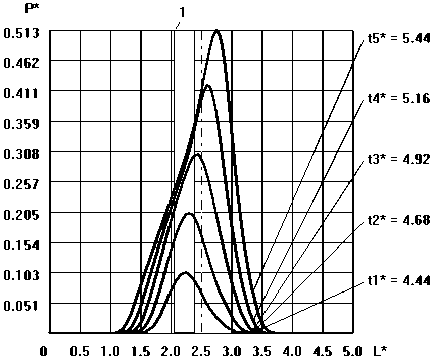
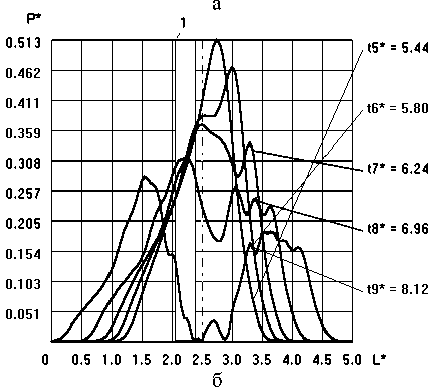
Рис. 3. Эпюры давлений на дне камеры МРБ для объемной модели:

а – процесс нарастания давления; б – процесс уменьшения давления; 1 – расположение источника Be(t) относительно оси разрядной камеры

Сравнительный анализ численных расчетов для плоской и объемной модели показал (см. рис. 2 и рис. 3), что при смещении разрядного промежутка относительно оси разрядной камеры влево приводит к появлению максимальной величины давления P ^* i max на преграде справа. Анализ временных характеристик P ^* max показывает (см. рис. 2 и рис. 3), что в плоской модели погрешность расчета P ^* max составляет порядка 87% по сравнению с объемной моделью, при этом время достижения P ^* max в плоской модели отличается от объемной на 0,4%, т.е. в динамическом режиме наблюдается качественное совпадение результатов расчета по давлению.

Несмотря на то, что объемная модель дает более точный количественный результат и является более информативной (результат можно просмотреть в трех плоскостях), для упрощения процесса исследований новых эффектов [4] дос- таточно использовать плоскую модель. Это связано с тем, что более важным является получение качественной наглядной интерпретации физической картины исследуемого динамического процесса, например, при электроразряде в жидкости. Плоская модель также позволяет исследовать физику процесса, т.е. выявить основные гидродинамические эффекты при электроразряде. Как показывают результаты расчётов, использование объемной модели не привносит новизны в полученные с помощью плоской модели результаты. В [11] исследовались процессы в камерах ЭИУ с учётом математической модели на основе применения метода инверсии для по-лубесконечных областей для границ Se(t) с возможностью устранения условия типа ∂ψ = 0 , т.е.

∂t для момента времени ti, связанного с выходом ударной волны на свободную поверхность жидкости. Это было необходимо для устранения волн разрежения в условиях частичного погружения камеры в жидкость.

Выводы:

• 1.    Полученные с помощью математической модели теоретические результаты расчётов позволяют дать как детальное описание исследуемых явлений, так и наглядную физическую интерпретацию экспериментально выявленного возникновения неравномерного распределения поля давления по поверхности преграды [4], снабжённой специальными датчиками.

• 2.    Результаты численных расчётов позволили теоретически подтвердить экспериментально установленный эффект [4], представить особенности исследуемого эффекта, установить асимметричную самофокусировку ударных волн в виде концентрации их энергий в нижней части цилиндрической камеры и определить возможности плоской и объемной моделей в исследуемом динамическом процессе.

• 3.    Эффект асимметричной самофокусировку ударных волн необходимо учитывать специалистам в решениях прикладных задач, связанных с

использованием специального вида камер, в условиях мощного электроразряда в жидкости.