Особенности распространения SH-волн в биморфной пьезоэлектрической/пьезомагнитной пластине из функционально градиентных материалов

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2025PNRPU MECHANICS BULLETIN

Исследование физических явлений при взаимодействии акустических поверхностных и объемных волн с электрическими и магнитными полями в пьезоэлектрических, диэлектрических, полупроводниковых и магнитострикционных материалах [1–6] заложило основу их использования в различных приложениях методов неразрушающего контроля, количественной ультразвуковой и лазерной ультразвуковой диагностики, акустической микроскопии. Обзор современных магнитоэлектроупру-гих (МЭУ) материалов и устройств на их основе приведен в [7; 8]. В последние годы, благодаря развитию технологии получения и использованию высококачественных МЭУ материалов и пьезоэлектрических (ПЭ)/пьезомагнитных (ПМ) структур, все большее внимание уделяется изучению внешних и внутренних факторов, влияющих на изменение их свойств и особенности распространения акустических поверхностных и объемных волн. Для адекватной оценки пьезоэлектрического и магнитоэлектрического эффектов необходимо привлечение точных аналитических или численно-аналитических решений задач магнитоэлектроупругости. В [9; 10] получены аналитические решения задач магнитоэлектроупругости для трехмерных анизотропных однородных и многослойных прямоугольных пластин [9] и бесконечно протяженных многослойных пластин [10], испытывающих действие как поверхностных, так и внутренних нагрузок. В [11] определены типы электромагнитных условий на поверхности полупространства с гексагональной (6 mm) симметрией материала, допускающих распространение сдвиговых горизонтально поляризованных поверхностных акустических волн (SH-ПАВ). В [12] на примере составной пластины из пьезоэлектрических и упругих материалов аналитически исследуется процесс распространения SH-ПАВ. Численно-аналитический метод ортогональных полиномиальных разложений для изучения динамических характеристик слоистых МЭУ-структур предложен в [13; 14]. Подход к получению новой формы фундаментального решения трехмерных задач динамической магнитоэлектроупругости представлен в [15]. В [16–19] получены и исследованы особенности SH-ПАВ в композитных МЭУ-струк-турах с учетом магнитоэлектрического эффекта в зависимости от параметров структуры и характера граничных условий. Проведено сравнение дисперсионных свойств трехслойных гетероструктур, выполненных из однородных ПЭ, ПМ и композитных слоев [16] в различном сочетании. В [17–19] исследованы особенности поведения SH-волн в композитных пластинах при различных электромагнитных условиях на свободных поверхностях. В [20–23] изучено поведение SH-волн в составных ПЭ/ПМ-пластинах при идеальных [20; 23] и неидеальных [21; 22] условиях на границе раздела. Показано влияние физических и геометрических параметров слоев на фазовые и групповые скорости первых мод скоростей SH-ПАВ, установлена возможность увеличения коэффициента магнитоэлектромеханической связи (КМЭМС) за счет изменения соотношения толщин слоев [23].

Появление и широкое использование новых высокотехнологичных функционально-ориентированных материалов с переменными свойствами привело к необходимости прогнозирования изменения их физических, технологических и прочностных качеств в зависимости от условий эксплуатации и характера внешних воздействий. Сложность возникающих при этом динамических задач состоит в невозможности построения аналитических решений для полуограниченных сред с изменяющимися в пространстве свойствами. Предположение о том, что все свойства материала изменяются по одной пространственной переменной с равной интенсивностью и одному закону приводит к существенному упрощению задачи, что исключает возможность качественной оценки результатов более сложного численного или численно-аналитического моделирования. В [24; 25] разработана теория распространения упругих волн в слоистой пластине с непрерывным и кусочно-непрерывным изменением свойств. Краевые задачи для пластины с различными условиями на внешних поверхностях приведены в терминах матриц переноса и импеданса, полученные дисперсионные уравнения анализируются как в обобщенном виде, так и в длинноволновом и коротковолновом приближениях. Сформулированы теоремы о поведении ветвей дисперсионных кривых для различных краевых задач слоисто-неоднородной пластины, высказано предположение о возникающем из-за анизотропии отталкивании ветвей дисперсионных кривых, приводящее к формированию террасирующих узоров в спектрах SH-волн неоднородных пластин. В [26] предложена математическая модель для исследования поведения волн Лява и SH-волн, распространяющихся в стратифицированных средах с моноклинной симметрией. Представлены аналитические и численные решения, полученные с применением метода модифицированной матрицы переноса и специального формализма. Для пластин из функционально градиентного пьезоэлектрического материала (ФГПЭМ) в [27] использован гибридный численный метод, основанный на сочетании метода быстрого преобразования Фурье и модального анализа. Исследовано влияние коэффициентов градиентности модулей при квадратичном изменении свойств материала по толщине.

В [28] при решении краевых задач с электрически открытыми и закороченными условиями использованы функции Эри. В [29–34] предложен численно аналитический подход, в основе которого лежит сведение краевой задачи к системе начально-краевых задач Коши относительно компонент тензора напряжений и смещений в сочетании с использованием высокоточных численных схем восстановления их решения. Такой подход позволил исследовать особенности распространения волн в неоднородных упругих и электроупругих средах с монотонным, немонотонным и кусочно-непрерывным изменением свойств [29; 30]. В рамках предложенного подхода в [31; 32] реализованы двух- и трехкомпонентные модели функционально градиентных материалов (ФГМ), в которых значения параметров основного материала изменяются до значений параметров материалов включений. Показано влияние характера и локализации неоднородностей на особенности поведения SH-ПАВ. В [33; 34] в рамках двухкомпонентной модели для составной пластины из неоднородных ПЭ и диэлектрического (ДЭ) материалов исследовано влияние характера неоднородности слоев, градиентности включений и их локализации на дисперсионные свойства пластины и скорости SH-ПАВ. Для биморфных ПЭ/ПМ-пластин в [35] рассмотрено влияние свойств ПЭ-слоя на поведение скоростей SH-ПАВ и КМЭМС при различных электрических и магнитных условиях на внешних поверхностях. Показано влияние упругих, ПЭ и ДЭ характеристик слоя на изменение дисперсионных свойств составных пластин, особенности поведения различных мод SH-ПАВ и КМЭМС.

Влияние неоднородности в МЭУ-пластине на скорости SH-ПАВ исследовано в [36]. Представление механического перемещения, электрического и магнитного потенциалов получены путем решения уравнений связанного поля в случае экспоненциального изменения свойств материала по толщине. Рассмотрено влияние неоднородности материальных констант на фазовую скорость в узком диапазоне низких частот. В [37] получено решение задачи о распространении гармонических волн в МЭУ-пластинах из функционально градиентных пьезоэлектрического и магнитострикционного материалов с изменением свойств по степенному закону. Использован метод разложения в ортогональные ряды полиномов Лежандра, исследовано влияние учета ПЭ- и ПМ-эффекта на скорости распространения волн. В [38] приведены результаты исследований влияния функционально градиентного промежуточного слоя на скорости SH-ПАВ в слоистых ПЭ/ПМ-цилиндрах. Рассмотрены семь видов функциональных зависимостей изменения свойств промежуточного слоя и четыре вида электромагнитных поверхностных условий. Установлено, что высшие моды ПАВ более чувствительны к градиентности изменения свойств, низшие моды – к электрическим и магнитным поверхностным условиям.

Настоящая работа посвящена исследованию влияния неоднородности ПЭ- и ПМ-слоев на распространение SH-ПАВ в составной МЭУ-пластине. Полагается, что

ПЭ-слой выполнен из различных видов керамики на основе PZT. Неоднородность ПМ слоя моделирует взаимопроникновение материалов слоев в узкой переходной области у границы раздела. На примере задачи с электрически закороченными и открытыми магнитными поверхностными условиями исследовано влияние характера неоднородности ПЭ- и ПМ-слоев пластины на скорости SH-ПАВ. Показано, что важную роль в их поведении играет не только характер, но и расположение неоднородности ПЭ слоя. Установлены особенности поведения скоростей в зависимости от характера неоднородности у границы раздела слоев.

1.    Постановка задачи

Рассматривается задача о распространении в направлении x1 SH-ПАВ в МЭУ-пластине, представляющей собой неоднородный ПЭ (0 < x2 < H1, | x1 |, | x3 | < «) и неоднородный ПМ (H2 < x2 < 0, | x1 |, | x3 | < ^) слои, жестко сцепленные между собой, внешние поверхности свободно контактируют с вакуумом (рис.1).

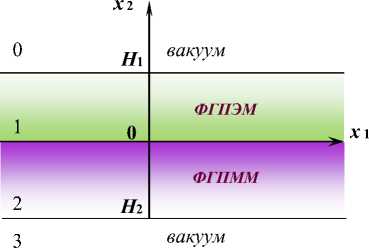
Рис. 1. Геометрия задачи

Fig. 1. Geometry of the problem

Полагается, что неоднородные ПЭ- и ПМ-слои выполнены из ФГПЭМ и ФГПММ. Изменение свойств слоев по толщине определены выражениями ( n = 1,2):

Р^{( n} ’ =p 0 n ’ F ⁿ ’ ( x 2 ) , c j ’ = c 0 ^{( n} ’ F ⁿ ’ ( x 2 ) , 4 ’ = e 0 ^{( n} ’ F ⁿ ’ ( x 2 ) , г j ’ =е 0 ⁽ n ’ F n ’ ( x 2 ) ,     (11)

4 ⁿ ’ = jⁿ ’ F fⁿ ’ ( x 2 ) , ц j ’ =ц j ^{( n} ’ F ( ⁿ ’ ( x 2 ) ,      .

e (²⁾ = 0, j ) = 0.

Здесь p0n’ - плотность, сjn’, e0(n’, fjn’ - компоненты тензоров упругих, ПЭ и ПМ констант, е jn’, ц jn’ -компоненты тензоров диэлектрической и магнитной проницаемости основных ПЭ (n = 1) и ПМ (n = 2) материалов пластины. Полагаем, что материалы слоев пластины имеют симметрию класса 6 mm, оси симметрии и поляризации направлены вдоль оси x3. Распространение волн вызвано действием удаленного источника гармонических колебаний. С учетом характера движения среды, зависимость от времени для всех параметров задачи представляется в виде (И - угловая частота):

f ( x i , x 2 , x 3 , t ) = f ( x i , x 2 , x 3 ) e " t .

Перемещения U kⁿ ’ ( x 1 , x ₂, x ₃, t ), электрический V^{( n} ’ ( x 1 , x ₂, x ₃, t ) и магнитный ^ ^{( n} ’ ( x 1 , x ₂, x ₃, t ) потенциалы удовлетворяют условиям ( n = 1,2 )

u1(n’ = 0, u2(n’ = 0, d(-) / dx3 = 0, u3(n’ = u3(n’(x1,x2)e-iИt, Ф(n’ = V(n’(x1,x2)e-i™t, (1-2) 4n ’=4n’ (x1, x 2) e - iИ t.

Поскольку рассматривается установившийся режим гармонических колебаний, экспоненциальный множитель далее опущен.

В квазистатическом приближении движение составной МЭУ среды описывается уравнениями [3–5]:

• ^{2 ( n} ’

• v - T ^{( n} ’ =p^{( n} ’ ^-u— , V - D ^{( n} ’ = 0, V - B ^{( n} ’ = 0, (1.3) Э t ²

Компоненты тензора напряжений ( т {р ¹’ ) векторов электрической ( d ( ⁿ ’ ) и магнитной ( b lⁿ ’ ) индукции определены соотношениями ( k , l , s , p = 1,2,3; n = 1,2):

_T ^{( n} ) __c^{( n}’Aⁿ ) _+e( ⁿ Ы ⁿ ) ₊ Aⁿ Ы ⁿ ) ¹ lP = c lksp u s , p ^{+ e}lkp V , p ⁺ J lPp V , p , j ^{( n}’-Aⁿ ) ⁽ n )__f^{( n} ’ ^{( n} )_J ⁿ ’ ^{( n} ’ d l = e lsp u s , p ^е lp V , p g lp ^V , p ,            ^(1-4)

_h ^{( n} ) _ A.ⁿ ) ^{( n} ) _ J ⁿ ) ^{( n} )       ^{( n} ) ^{( n} )

^bl = Asp u s , p g lp ^V , p ^Ц lp ^V , p ■

Для вакуума справедливо ( m = 0,3):

Дф⁽ m ’ = 0, Д^⁽ m ’ = 0.              (1.5)

В выражениях (1.3)-(1.5) V - оператор Гамильтона; _T( n )_{, D}( n ) и B^{( n )} – тензор напряжений, векторы индукции электрического и магнитного полей n -й составляющей структуры; u^{( n )} – вектор механических перемещений; V ^{( n} ’ и V ^{( n} ’ - электрический и магнитный потенциалы, определяющие векторы напряженности магнитного H^{( n} ’ =-Vv ^{( n} ’ и электрического E^{( n} ’ =-Vv ^{( n} ’ полей; P^{( n} ’   пттлтиллтк a⁽ n ’ ⁽ nn ’ fnn ’   глмплирптт>т тртллли

– плотность, c_lksp , e_lkp , f_lkp – компоненты тензоров упругих ПЭ- и ПМ-констант, е⁽ pn ’, ц p ’ - компоненты тензоров диэлектрической и магнитной проницаемости, g lp ’ - компоненты тензора магнитоэлектрических констант материала -й составляющей структуры. Участвующий в (1.5) оператор Лапласа с учетом (1.2) имеет вид Д = d ² / d x ₁ ² + d ² / d x 2 . Константы ПЭ- и ПМ-материалов симметрии 6mm в нотации Фойгта удовлетворяют условиям [3; 4]:

r(n)        n)         n) J n)         n) Дn)         n)

c 1111 = c 2222 = c 11 , c 3333 = c 33 , 4122 = c 2211 = c 12 ,

(n) - A n)         n)         n)

c 1133 = c 3311 = c 2233 = c 3322 = c 13 ,

(n) - A n)         n)         n) n)         n)         n) n)

c2323 = c2332 = c3223 = c3232 = c3113 = c3131 = c1313 = c1331 = c44 , r (n) = J n) = J n) = J n)           n )-4 n >)

c 1212 = c 1221 = c 2112 = c 2121 = 0’ ⁵ ( ^c11 c 22 ) ,

e(1) e е e J1) е e е e131 = e311 = e113 = e15 , e232 = e322 = e223 = e15 ,

_g( ¹ ) - J¹) __g( ¹ ) - J¹) - J¹ )

e113 = e223 = e311 = e322 = e31 , g (1) - J1) gW-gO) J1)-J1) e333 = e33 , °11 = °22 , P11 = H22 , f (2) _ 42) _ Д2) _ Д2) Д2) _ 42) _ rf) _ rf)

f 131 = f 311 = f 113 = f 15 , f 232 = f 322 = f 223 = f 15 , f (2) _ Д2) _ Д2) _ Д2) _ z(2) f 113 = f 223 = f 311 = f 322 = f 31 , f (2) _ f(2)  J2) _ ц(2)  g(2) _ g(2)  „(n) _ „(n) _ „(n) _ „(n)

^f 333 = ^f 33 , P 11 =^ 22 , ° 11 = ° 22 ’ ^g 11   = ^g 22 = ^g 33 = ^g 1 ^.

Следуя [18], полагаем, что магнитоэлектрические ( n ) Л константы материалов g } - 0 .

Замыкает постановку краевых задач о движении составной МЭУ среды задание граничных условий [4, 5]: на границе раздела ФГПЭМ и ФГПММ слоев выполняются условия сцепления:

x = 0: N • T ⁽¹⁾ = N • T ⁽²⁾ , N • D ⁽¹⁾ = N • D ⁽²⁾ ,

²                                                    (1.6)

B(1) = N • B(2), u(1) = u(2), ф(1) =ф<2), ф'1    4r, внешние поверхности структуры свободны от механических нагрузок:

x ₂ = H ₁: N • T ⁽¹⁾ = 0; x ₂ = H ₂: N • T ⁽²⁾ = 0. (1.7)

В зависимости от типа электрических и магнитных условий на внешних поверхностях [5] рассмотрим следующие задачи:

I - электрически закрытая, магнитно-открытая задача ( so ):

x ₂ = H j : ф^{( 1 )} = 0, у^{( 1 )} = 0;

x ₂ = H ₂

II - электрически дача ( os ):

(1.8)

: ф^{( 2 )} = 0, v^{( 2 )} = 0.

открытая, магнитно-закрытая за-

x ₂ = H j : ф^{( 1 )}

= ф(0), N• D(1) = N• D(0), и' U0), N • B(1) = N • B(0);

’                                   (1.9)

x ₂ = H ₂: ф^{( 2 )}=ф^{( 3 )} , N • D ⁽²⁾ = N • D ⁽³⁾, ф^{( 2 )}=ф^{( 3 )} , N • B ⁽²⁾ = N • B ⁽³⁾.

III - электрически и магнитно- открытая задача ( oo ):

x ₂ = H : ф^{( 1 )} = ф^{( 0 )} ,   N • D ⁽¹⁾ = N • D ⁽⁰⁾ , ф ¹ = 0;

• ^{2      1} -     - ■                      , v ,   (1.Ю)

x 2 = H ₂ : ф^{( 2 )} = ф^{( 3 )} , N • D ⁽²⁾ = N • D ⁽³⁾ , ф ² = 0.

IV - электрически и магнитно-закрытая задача ( ss ):

x ₂ = H ₁ : ф^{( 1 )} = 0, ф ' ¹ = Ф 0 , N • B ⁽¹⁾ = N • B ⁽⁰⁾ ;

x ₂ = H ₂ : ф^{( 2 )}= 0, ф ' ^{2 )}=V^{( 3 )} , N • B ⁽²⁾ = N • B ⁽³⁾.        ⁾

Здесь N - вектор нормали к поверхностям и границе раздела. Для удобства дальнейшего изложения введем расширенный вектор перемещений uem(n) = { u (n), u 4 n) = ф( n), u 5 n) =^( n)} n-й составляющей пластины. С учетом (1.2) и свойств материалов структуры отличные от нуля компоненты тензора напряжений и векторов электрической и магнитной индукции (1.4) принимают вид (k = 1,2; m = 0,3):

для PE

(1) -с(1)м(1) ^W/) тk3 = c44 u3,k + e15 u4,k , d!” = >?M?u!'!. bP =-Ф‘Л'?!;   r ’ k         15 3,k       11 4,k ' k          < 11 5,k '

для PM

_T ^{(2 )}_{= r}( ²U²⁾ . /(² )_;y^{( 2 )} Л^{2 )}₌ _p( ²U^{2 )}

Tk3 = c44 u3,k + f 15 u5,k ’ dk = °11 u4,k’ b (2) = H2M2)_U^^          (. )

b k = f 15 ^u 3, k ^H 11 ^u 5, k ;

для вакуума d2m) =-e0u4m?, b2m) =-H0u5m2).         (1.14)

Здесь e ₀, Ц ₀ - диэлектрическая и магнитная проницаемости вакуума.

Далее используются безразмерные параметры [35]:

l'= l / H , р ' ^{( n} ) = р^{( n} ) / р 0 ^{2 )} , c jn ) = c j ) / c ₄ ⁰ < ²⁾ ,

/⁽ n ) ₌ J n k / o⁽²⁾ p'⁽ n ) = p⁽ nj ² /r⁰⁽²)

ej      eij S e ' c 44 ’ ° ij °ij S e ' c 44 ’ f'(n)_ f( nhi /г0(2) ||'(n )_||( nhi 2 / 0(2)

• ^f j = f ij ^S m / c 44 ’ ^H ij = H ij ^S m / c 44 ’ ф! n ) =ф ⁽ n ) / ( S e H ) , ф ⁽ n W n ) / ( S m H ) ,

  где H - характерный линейный размер, S _e = 10¹⁰ [В/м], S _m = 10⁷ [А/м] - метрические множители, к ₂ =ю H / V^ -безразмерная частота, V^ = с J42 ) / р 0^{2 )} - скорость объемной сдвиговой волны основного ПМ материала. Далее штрихи опущены.

С учетом новых обозначений, условий (1.1) и представлений (1.12)-(1.14) уравнения движения (1.3), (1.5) в безразмерных переменных принимают вид:

для неоднородного ПЭ-слоя:

VГгwj¹) +ЛМ¹) 1+Z¹)          J¹) - -Л¹) к²-, ?)

^1 с44 u3,kk + e15 u4,kk I + c44,2u3,2 + e15,2u4,2 = р K2 u3 , k =1LJ

У ГeWz/1) -ew«(1) 1 + e,(1) z?) -e(1) z?) -0       (1.15)

^\e15 u3,kk °11 u4,kk I + e15,2u3,2 °11,2u4,2 = 0, k=1LJ

Г- n^M¹) 1-ц( 1 ) J1 ) / . ^H 11 u 5, kk    ^H 11,2 u 5,2 = ⁰;

k = 1

для неоднородного ПМ-слоя:

Y Г C^{( 2}M2 ) + f( ²M2 ) 1 + _C( ² ) Z/( 2 )+ f^{( 2} )_U( ² )--o( 2 ) K2 «( 2 ) / \ с 44 u 3, kk ⁺ f 15 u 5, kk I ⁺ c 44,2 u 3,2 ^{+ f} 15,2 u 5,2 = ^{р K} 2 u 3 ’ k =1 ^{L                         J}

Y Г- p( 2 ),/²) 1- p( 2 )„( 2 )__n                  (1.16)

/ \ ° 11 ^u 4, kk I ° 11,2 u 4,2 = °’ k =1 ^{L             J}

X Г f ) u . h ' u Ш + 4²) u (² -p ( 2 )2 u (² = 0;

15   3, kk 11 5, kk 15,2 3,2      11,2 5,2

для вакуума ( m = 0,3):

S u 4 "к = 0, S u 5 k = 0.         (1.17)

k = 1                k = 1

Граничные условия (1.6)–(1.11) записываются в виде: механические условия на внешних поверхностях:

X 2 = H 1 : ^ 25 = 0;   x 2 = H 2 : 43’ = 0;     (1.18)

на границе раздела:

• ( 1 )    __T2 J¹) _d⁽2)           _b('²')

x 2 = 0 • ^T 23 = ^T 23 >  d 2 = d 2 , b 2 = ^b2 ,

• ( 1 )         ( 2 )       ( 1 )         ( 2 )       ( 1 )         ( 2 )           ⁽ ■ )

u

3 — u з , u 4 — u 4 , u 5 — u 5 ■

Электрические и магнитные условия на внешних поверхностях:

I – электрически закрытая, магнитно-открытая задача ( so ):

x, = H • u ^{( 1 )} = 0, u ^{( 1 )} = 0;

^{214    5}          (1.20)

x ₂ = H ₂ • u 4^{2 )} = 0, u 5^{2 )} = 0.

II – электрически открытая, магнитно-закрытая задача ( os ):

X=H-U(1)=M(0)            «/W0» /,<1)=/,<0)-

• x 2   ^J1[ • ^u 4      ^u 4   , ^u2     ^u2 , ^u 5      ^u 5   , ^2     ^2   ^;

■ )           ;,-^{:                                                                                                                              .}

x ₂₂: u ₄ u ₄,_{2    2}, u ₅ u ₅,₂₂.

III – электрически и магнитно- открытая задача ( oo ):

x ₂ = H 1 • u 41 ) = u 40 ), d 21 ) = d 20 ), u 51 ) = 0;

x 2 = H 2 • ^u 42 ) = ^u 43 ), d 22 ) = d 23 ), u 52 ) = 0.

(1.22)

IV – электрически и магнитно- закрытая задача ( ss ):

x ₂ = H 1 • u 41 ) = 0, u 51 ) = u 50 ),   b 21 ) = b 20 );

x 2 = h 2 • ^u 42 ) = 0, ^u 52 ) = ^u 53 ), ь 22 ) = ь 23 ).

(1.23)

2.    Решение задачи

Решение задач I – (1.15), (1.16), (1.18) – (1.20), II – (1.15) – (1.17), (1.18), (1.19), (1.21), III– (1.15) – (1.17), (1.18), (1.19), (1.22) и IV – (1.15) – (1.17), (1.18), (1.19), (1.23) строится в пространстве образов Фурье ( а - параметр преобразования по координате x ₁ ). Смещение, электрический и магнитный потенциалы для составляющих пластины и вакуума будем искать в виде ( p = 3,4,5; g = 4,5,6; 5 = 4,5; n = 1,2 )•

U«(«, x 2 ) = Sckn’y«(а, x2 )• k=1

U_s ⁽⁰⁾ ( а , x ₂ ) = C < ⁰⁾ e ² , U^ ( а , x ₂ ) = C<³⁾e ° x ² .

(2.1)

Функции y (”к*(а, x 2) в представлении (2.1) являются линейно независимыми решениями задач Коши с начальными краевыми условиями yp""k)(а,0) = 5pk для уравнений

Y ⁽ " ’‘= R ⁽ " > ( а , x ₂ ) Y ⁽ " ’,                 (2.2)

Y ⁽ n )

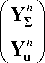
Y = { ® Г 3 ⁽ n ’ , d 2 ⁽ n ’ , b F ⁽ n ’f,

n

u

(2.3)

' U 3 " ’ , U 4 n ’ , U 5 n ’

Здесь 0 F ₃ ⁽ " ’, D 2 ⁽ " ’, B 2 ⁽ " ’, U P" ’ - трансформанты Фурье компонент тензора напряжений, векторов электрической и магнитной индукции (1.12)–(1.14) и расширенного вектора смещений; 5 _pk - символ Кронекера. Матрицы R ⁽ " ’ ( а, x ₂ ) имеют вид^

' 0 0 0 c44’а2 -р(1’к2 е(5’а2 0 0 0 0 е(5’а2 -Еп’а2 0 (2.4) R(1’(а, x 2 ) = 0 Е?? / re 0 e(5’ / re 0 0 0 0 0 0 -^v 0 e(5’ / re -c44 / re 0 0 0 0 0 0 -1/h!? 0 0 0 '   0 0 0 0 0 0 r (2U 2 — гЯ V2 C44 а   p  K2 0 0 -^’а2 f 52’а2 0 (2.5) R(2)(а, x2 ) = и(?/ rm 0 0 0 f(2) / rm f15 /r0 А .'■ 0 0 0 а 0 0 -1/ 0 0 0 0

Следует отметить, что уравнения (2.2) с обозначениями (2.3)–(2.5) представляют собой системы обыкновенных дифференциальных уравнений (ОДУ) 1-го рода 6-го порядка с переменными коэффициентами. Линейно независимые решения таких систем строятся на основе численного решения набора задач Коши с начальными условиями при фиксированных значениях параметра а . Для их решения могут быть использованы различные численные методы. В настоящей работе, как и в работах [29–34], при решении (2.2) использован метод Рунге – Кутты – Мерсона 5-го порядка, с помощью которого восстанавливаются значения ygk (а,x₂) на отрезке x₂е [0,H1 ] для ПЭ и ygk’ (а,x₂) на отрезке x₂е [0,H₂] для ПМ слоев. Далее, подставляя решения (2.1) в граничные условия задач I, II, III и IV, для вычисления неизвестных коэффициентов ck"’ и egm’ получаем однородные системы линейных алгебраических уравнений. В зависимости от типа рассматриваемых задач условие нетриви-альности решения приводит к дисперсионному уравнению задачи. Далее, после определения всех неизвестных и применяя к (2.1) обратное преобразование Фурье, получаем решение рассматриваемых задач.

3.    Дисперсионные уравнения

Представим дисперсионные уравнения задач I, II, III и IV для составной МЭУ пластины в виде [33; 35]:

det Ar (a, k₂ ) = 0, r = 1,П,Ш,ГУ.        (3.1)

Структура и размерность матриц			Ar(a, x2)	опреде-
ляются граничным (1.18)–(1.23): AI =		и условиями рассм ' PeI (H1 )       0    ' Pe (0)   -Pm (0) . 0     Pm (H2) j	атриваемых задач ,
	' PJI ( H1 )	0 Gem ( h1)	0	2
A11=	Pe (0) к0 ' Pe111( H1 )	-Pm (0)      0 Pm (H2)     0 0      Ge (H1 )	0 GeIm ( H2: 0 Л	J	, (3.2)
A111=	Pe (0) 4    0 ' PeIV ( H1 )	-Pm (0)      0 Pm1(H2)     0 0     Gm ( H1	0 Ge ( H2 )j 0	, 2
AIV =	Pe (0) ^    0	-Pm(0)      0 PmV (H2)     0	0 Gm (H2	) J	.

Матрицы А^IIIи A^IVимеют размерность 14×14, A^Iи AII - соответственно 12*12 и 16*16. Матрицы P_e(0) и Pm ( 0) , в силу условий сцепления на границе раздела (1.19) и принятых начальных условий задачи Коши для уравнения (2.2), являются единичными матрицами размерности 6*6: Pe (0) = Pm (0) = I. С учетом (2.1) матрицы Pe¹¹(H1) и Pm¹(H₂) размерности 5*6 имеют вид:

	( ( n ) У11)	( n ) У12)	( n ) У13)	( n ) У14)	( n ) У15)	( n ) У16)
	(n) y 21)	(n) y 22)	(n) у 23)	(n) y 24)	(n) y 25)	(n) y 26)
P" (Hn ) =	(n) y 51	(n) У 52)	(n) У 53)	(n) y 54)	(n) y 55)	(n) y 56)	(3.3)
	(n) У 31)	(n) У 32)	(n) У 33)	(n) У 34)	(n) У 35)	(n) y 36)
	(n) 1У 61)	(n) У 62)	(n) У 63)	(n) У 64)	(n) У 65)	(n) У 66) >

	(	0 -e0ay(1)	0 0
Gem ( h1 )=	<	-Yw 0 0 20 e0ay(2)	0 pa.'/' -Y0» 0 2 0	J
Glm (H 2 ) =		-Y(2) 0 40	0 pa.'/2 -y(2)j	,

(3.4)

где y⁽¹⁾ = e^aH 1, Y⁽2) = e^aH²■ Векторы Ge(H1), Ge(H2) получаются из матриц GIm (H 1) и Gem (H2) путем вычеркивания 2-го столбца и 4-й строки, Gm(H1), Gm(H2) – путем вычеркивания 1-го столбца и 2-й строки.

4. Численный анализ

Для исследования особенностей распространения SH-ПАВ в биморфной пластине из ФГПЭМ/ФГПММ рассмотрена двухкомпонентная модель ФГМ [31; 32]. В рамках модели свойства изменяются по толщине от параметров основного материала до параметров материала включения. В качестве основных материалов ПЭ- и ПМ-слоев использованы пьезокерамика PZT-5H (m1) [3] и высокоскоростной пьезомагнитный материал CoFe2O4 (m4) [10; 23]. При выборе материалов включений ПЭ-слоя – m2 (PZT DL-61HD [39]) и m3 (гипотетический материал) учитывалось незначительное различие упругих модулей при существенном разбросе пьезоэлектрических и диэлектрических констант. Скоростные характеристики включений определялись условиями |V - V 21 ^ V - Vm31 и у™1 - Vm21 = Vsm■ -vm3. неод- нородность ПМ-слоя моделировала проникновение ПЭ-материала в узкой области у границы раздела. В рамках этого подхода упругие параметры материалов включений ПМ-слоя m41, m42 и m43 выбирались равными упругим параметрам m1, m2 и m3 и сохранялось соотношение скоростных характеристик включений слоев, в частности vm / vm2 = vm41 / vm42, vm / vm3 = vm41 / vm43. Пара-SS SSSS SS метры материалов и скорости сдвиговых волн без учета и с учетом ПЭ и ПМ свойств приведены в таблице.

В таблице: v_s = ^c44 / p , v_Se = ^(c₄₄+(e₁₅)² / e_n) / p , ^vSm = ( c44 ⁺⁽f.5 ) / И11 ) / ^p.

Следуя [31–34], участвующие в (1.1) функции Fsⁿ), s = p, c, e, e, f,p представим в виде:

Fsn)= gS + g2F (x2).                (4.1)

Параметры g¹_s , g_s² – определены значениями модулей основного материала и материалов включений; F (x2) - функциональная зависимость изменения параметров по толщине слоя, которая определяет локализацию включения и размер зоны перехода одного материала в другой.

В рамках двухкомпонентных моделей исследованы:

– пластины ФГПЭМ/ПМ с различной локализацией включений по толщине ПЭ-слоя:

m1-m2/m4 – неоднородный ПЭ-слой m1 с высокоскоростным включением m2 и однородный ПМ-слой m4;

m1-m3/m4 – неоднородный ПЭ-слой m1 с низкоскоростным включением m3 и однородный ПМ слой m4.

– пластины ФГПЭМ/ФГПММ (включения ПМ- и ПЭ-слоев расположены в окрестности границы раздела.):

m1/m41-m4 – однородный ПЭ-слой m1 и неоднородный ПМ-слой m4 с включением m41;

m1-m2/m42-m4 – неоднородный ПЭ-слой m1 с включением m2 и неоднородный ПМ-слой m4 с включением m42;

m1-m3/m43-m4 – неоднородный ПЭ-слой m1 с включе нием m3 и неоднородный ПМ-слой m4 с включением m43.

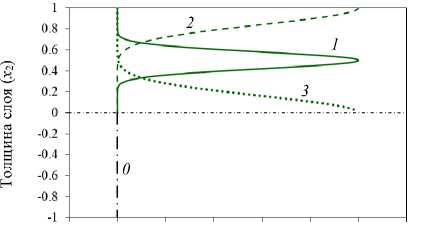
Функциональные зависимости изменения свойств по толщине рассматриваемых пластин приведены на рис. 2.

Параметры материалов

-0.2       0       0.2      0.4      0.6      0.8       1       1.2

Функциональная зависимость F (x2)

Функциональная зависимость F (x 2)

b

Безразмерный параметр с 44 (x 2)

Material parameters

Параметр m1 m2 m3 m4 m41 m42 m43 ρ [кг/м3] 7500 8200 7560 5300 6150 7900 6160 c44 × 1010 [Н/м2] 2.3 3.9 1.32 4.53 2.3 3.9 1.32 e15 [Кл/м2] 17 33.1 6.46 0 0 0 0 ε11 × 10-10 [Кл2/(Н·м2)] 151 249 80.6 0.8 24 45 16 f15 [Н/(А·м)] 0 0 0 550 300 450 200 µ11 × 10-6, [Н·с2/Кл2] 5 5 5 -590 -150 -470 -80 VS [м/с] 1751 2181 1321 2924 1934 2222 1464 VSe, [м/с] 2370 3182 1559 VSm, [м/с] 2907 1908 2210 1436 c                                                           d

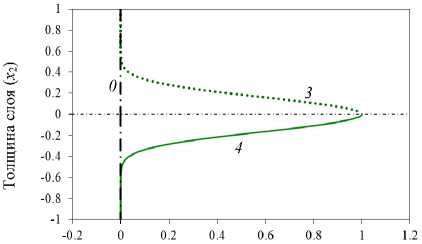
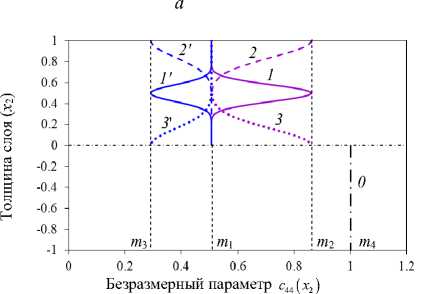
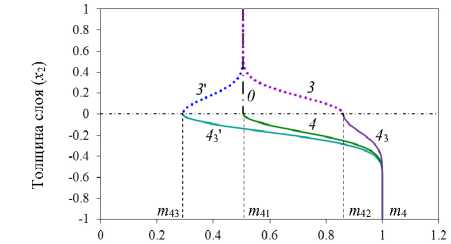
Рис. 2. Графики функциональных зависимостей изменения свойств в пластине: а – изменение свойств в ПЭ-слое; b – изменение свойств в ПЭ- и ПМ-слоях; c, d – изменение c44(x2) по толщине пластины

Fig. 2. Graphs of functional dependencies of changes in properties in the plate: a – changes in properties in the PE layer; b – changes in properties in the PE and PM layers; c, d – changes in c44(x2) across the plate thickness

На рис. 2, а, b, представлены функциональные зависимости изменения свойств ПЭ-слоя с однородным (см. рис. 2, а) и неоднородным (см. рис. 2, b) ПМ-слоем пластины. Цифрами 1, 2, 3 на рисунках отмечены кривые с локализацией неоднородности ПЭ-слоя в середине (сплошная линия 1), у внешней поверхности (штриховая линия 2) и у границы раздела (пунктирная линия 3). Кривая 4 (сплошная линия, см. рис. 2, b) отвечает изменению свойств ПМ слоя с локализацией неоднородности у границы раздела. Цифрой 0 (штрихпунктирные линии) на рисунках отмечены кривые для однородных материалов. На рис. 2, с, d, показано изменение безразмерного параметра c44 (x2) по толщине пластины в случае ФГПЭМ/ПМ (см. рис. 2, с) и ФГПЭМ/ФГПММ (см. рис. 2, d). На рис. 2, с, локализация включений m2 (кривые 1, 2, 3) и m3 (кривые 1', 2', 3') отмечена сплошными, штриховыми и пунктирными линиями в соответствии с рис. 2, а. На рис. 2, d, изменение c44 (x2) в случае пластины m 1/m₄₁-m4 отмечено штрихпунктирной линией 2 и сплошной линией 4, в случае m1–m2/m42–m4 – пунктирной линией 3 и сплошной линией 43, в случае m1–m3/m43–m4 – пунктирной линией 3' и сплошной линией 43'.

Из графиков следует, что свойства биморфной пластины из неоднородных материалов определяются как характером изменения параметров материала, типом, величиной и расположением неоднородности (F (x2)), так и соотношением параметров основного материала и материалов включений ( g1s, gs2 (4.1)).

Влияние характера и локализации неоднородности биморфной пластины на особенности распространения SH-ПАВ демонстрируются на примере задачи I (so) с электрически закрытыми и магнитно-открытыми условиями на внешних поверхностях. На рисунках приведены зависимости относительных фазовых скоростей VI / V(2 от частоты К ( УГ = к, / Zr, r = I, II, III, IV,

FS               2 F 2   ,    ,,  ,   ,

Zr - нули дисперсионного уравнения (3.1) с обозначениями (3.2) – (3.4)).

• 4.1.    Влияние области локализации неоднородности ПЭ-слоя

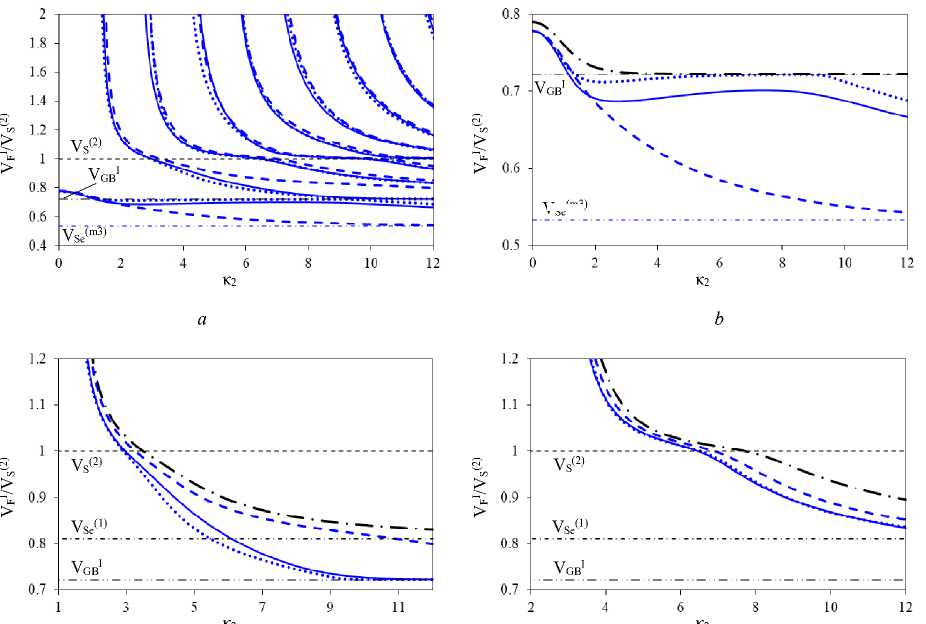
На рис. 3, а–d, показано влияние локализации включения на фазовые скорости V_F^I SH-ПАВ в случае m1– m2/m4. Расположение неоднородности отмечено сплошными, штриховыми и пунктирными линиями, соответствующими кривым 1, 2, 3 на рис. 2, а, c. Штрихпунктирная линия на рис. 2, b–d, отвечает пластине m1/m4. На рис. 3, b–d, приведено изменение скоростей 1-х, 2-х и 3-х мод.

d

Рис. 3. Влияние локализации высокоскоростного включения на скорости SH-ПАВ: а, b, c, d – скорости 1-х, 2-х и 3-х мод

Fig. 3. Effect of high-speed inclusion localization on SH-SAW velocities: a, b, c, d are the velocities of 1st, 2nd and 3rd modes

Из анализа рис. 3, а–d, следует, что влияние локализации неоднородности носит сложный характер и по-разному сказывается на поведении скоростей в различных диапазонах частот. Для высокоскоростного включения m2 характерно: в области частот выхода 2-й и 5-й мод влияние локализации невелико, на частоты выхода 3-й и 7-й мод в большей степени влияет срединная, 4-й и 8-й мод – приграничная локализация (см. рис. 3, а). По сравнению с пластиной m1/m4, в данном случае частоты выхода мод сдвигаются в область более высоких значений. Начиная с 6-й моды, сдвиг становится существенным. Для 1-х мод (см. рис. 3, b) – начальное значение VFI больше начального значения скорости в пластине с m1/m4 (штрихпунктирная линия). С ростом частоты в случаях приграничной и срединной локализации (пунктирная и сплошная линии) скорость VFI уменьшается до значения VGIB (скорость волны Гуляева – Блюштейна в материале m1 с коротко замкнутой поверхностью [4]). При поверхностной локализации (штриховая линия) после падения VFI в низкочастотном диапазоне наблюдается ее рост до максимального значения превышающего vSe^ и последующее постепенное уменьшение VFI на более высоких частотах. Для 2-х мод (см. рис. 3, с) при любом расположении m2 асимптотические значения VFI превосходят vSSe1. Влияние локализации сказывается в области средних и высоких частот. Для 3-х мод (см. рис. 3, d) в случае приграничной и срединной локализации включения в окрестности VS2 наблюдается появление «террасных» участков – диапазонов частот, на которых VFI изменяются незначительно V/ = V^ .

На рис. 4, а–d, продемонстрировано влияние локализации включения на фазовые скорости SH-ПАВ в случае m1–m3/m4. Сплошными, штриховыми и пунктирными линиями отмечено расположение неоднородности в середине ПЭ-слоя, у поверхности и границы раздела слоев (кривые 1, 2, 3 на рис. 2, а, и кривые 1', 2', 3' на рис. 2, с). На рис. 4, b – d, представлено поведение скоростей 1-х, 2-х и 3-х мод. Штрихпунктирной линией отмечено поведение скоростей в случае пластины m1/m4.

Из анализа рис. 4, а – d, следует что наличие низкоскоростного включения m3 в ПЭ-слое сдвигает частоты выхода мод SH-ПАВ в сторону более низких значений по сравнению с пластиной m1/m4. С ростом номера моды, начиная с 5-й, сдвиг частоты выхода становится значительным.

VSe(m3)

d

Рис. 4. Влияние локализации низкоскоростного включения на скорости SH-ПАВ: a, b, c, d – скорости 1-х, 2-х и 3-х мод

Fig. 4. Effect of low-speed inclusion localization on SH-SAW velocities: a, b, c, d are the velocities of 1st, 2nd and 3rd modes

Отметим, что влияние локализации включения на сдвиг частот выхода мод ПАВ носит неравномерный характер, т.е. в зависимости от расположения неоднородности меняется диапазон частот между выходом различных мод ПАВ. Для 1-х мод (см. рис. 4, b) – начальное значение V_F^I меньше начального значения скорости в пластине m1/m4 (штрихпунктирная линия), определяется параметрами включения и не зависит от его локализации. С ростом частоты в случае поверхностного расположения включения m3 скорость V_F^I падает, приближаясь к значению V^m³). В случае приграничной локализации после падения скорости в области низких частот наблюдается диапазон частот, в котором VI ~ VGIB , скорости 1-й и 2-й мод принимают близкие значения. Дальнейшее увеличение частоты приводит к выходу 2-й моды на значение скорости V_G^I_B , скорость 1-й моды становится меньше. При срединной локализации этот эффект менее выражен. Для 3-х мод характерно более быстрое по сравнению с пластиной m 1/ m 4 падение скорости до Vs1, перегиб в окрестности V^ происходит на более низких частотах (см. рис. 4, d).

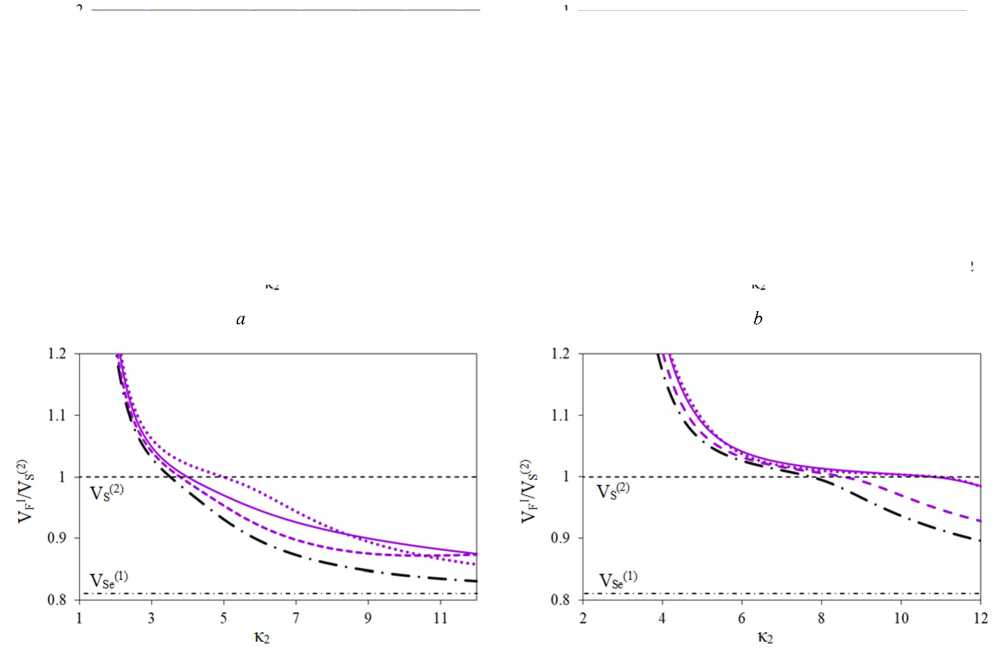
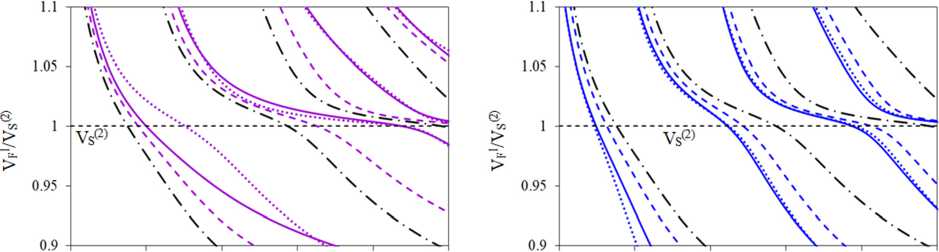
Из сравнения рис. 3, а, и рис. 4, а видно, что наличие как m2, так и m3 включений в ПЭ-слое приводит к появлению в окрестности V^ «террасных» участков. На рис. 5, а, b, приведены фрагменты рис. 3, а, и рис. 4, а, для скоростей 2-х, 3-х, 4-х и 5-х мод ПАВ в окрестности VS⁽²⁾.

Из рисунков видно, что в случае пластины m1–m2/m4 с приграничной или серединной локализацией включения «террасные» участки в окрестности V^ появляются на 3-й моде ПАВ (см. рис. 5, а). В случае m1–m3/m4 такие участки появляются на 5-й моде, в случае пластины m1/m4 – на 4-й моде ПАВ. Следует отметить, что результаты, полученные для скоростей SH-ПАВ МЭУ пластины ФГПЭМ/ПМ, хорошо согласуются с результатами [34] для пластины с неоднородными ПЭ- и ДЭ-слоями с учетом различий параметров ПМ- и ДЭ-слоев.

• 4.2.    Влияние неоднородности ПЭ и ПМ слоев

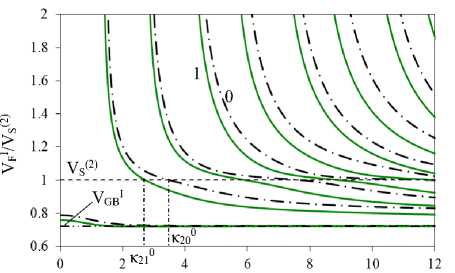
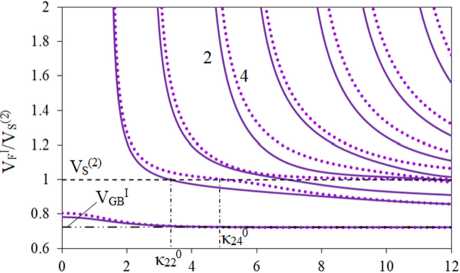
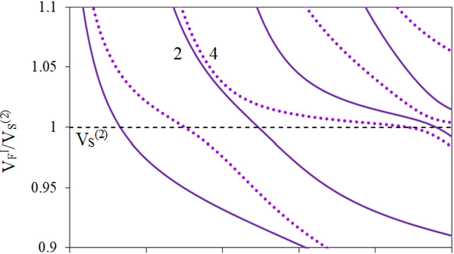
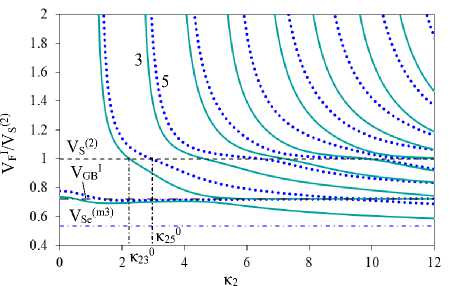
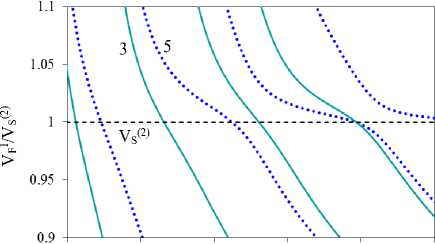
На рис. 6 и 7 проиллюстрировано влияние характера неоднородности пластины ФГПЭМ/ФГПММ на скорости SH-ПАВ. Функциональные зависимости изменения свойств по толщине соответствуют зависимостям рис. 2, b, и изменению параметров рис. 2, d. Сплошными линиями отмечены скорости в пластинах m1/m41–m4 (кривые 1 на рис. 6, а, b), m1-m2/m42-m4 (кривые 2 на рис. 6, c, d) и m1–m3/m43–m4 (кривые 3 на рис. 6, e, f). Для сравнения пунктирными линиями отмечены скорости SH-ПАВ пластины m1–m2/m4 (кривые 4, рис. 6, c, d) и пластины m1– m3/m4 (кривые 5, рис. 6, e, f). Штрихпунктирные линии на рис. 6, а, b, отвечают скоростям пластины m1/m4. На рис. 6, b, d, f, представлены соответственно фрагменты рис. 6, а, b, c, для скоростей 2-х, 3-х, 4-х и 5-х мод ПАВ в окрестности VS⁽²⁾.

Из рис. 6, а–f видно, что наличие неоднородностей ПЭ- и ПМ-слоев, расположенных у границы раздела в биморфной пластине, приводит к сдвигу частот выхода новых мод и частот (K0i) пересечения скоростей ПАВ с VS² в сторону более низких значений. С ростом частоты сдвиг увеличивается. Имеет место падение скоростей SH-ПАВ относительно пластин с однородным ПМ слоем. Из анализа рис. 6, b, d, f, видно, что наличие в окрестности границы раздела включений, для которых Vmi< V^²² (см. таблицу), приводит к сглаживанию поведения кривых скоростей в окрестности Vs²: появление «террасных» участков отмечается на модах с более высокими номерами.

2          4 б 8          10         12               2          4          6          8          10         12

К2                                                               К2

• а                                                               b

Рис. 5. Влияние локализации включений на скорости SH-ПАВ в окрестности VS⁽²⁾: а – высокоскоростное включение; b – низкоскоростное включение

Fig. 5. Effect of localization of inclusions on SH-SAW velocities in the vicinity of Vs⁽²⁾: a – high-speed inclusion; b – low-speed inclusion

а

2           4           б           8          10          12

κ2

K2

b

2           4           6           8           10          12

К2

c

d

2          4          б          8         10         12

κ2

e                                                                        f

Рис. 6. Влияние неоднородности ПЭ- и ПМ-слоев на скорости SH-ПАВ. Включения расположены в окрестности границы раздела: а, b – пластины m1/m41–m4 и m1/m4, c, d – пластины m1–m2/m42–m4 и m1–m2/m4, e, f – пластины m1–m3/m43–m4 и m1–m3/m4

Fig. 6. Effect of heterogeneity of PE and PM layers on SH-SAW velocities. Inclusions are located near the interface: a, b plates m1/m41–m4 and m1/m4; c, d plates m1–m2/m42–m4 and m1–m2/m4, e, f, plates m1–m3/m43–m4 and m1–m3/m4

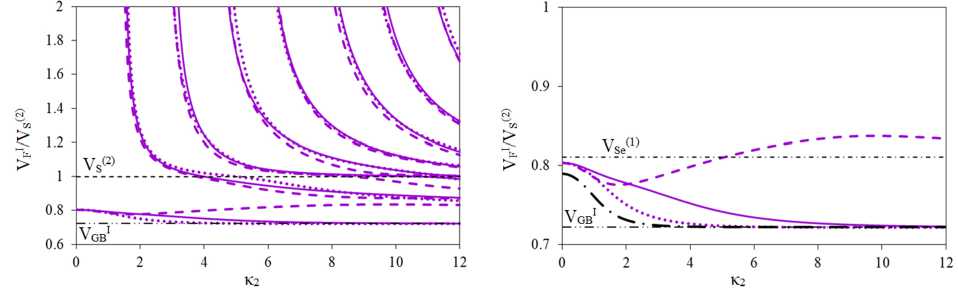
Отдельно отметим особенности поведения скоростей первых мод SH-ПАВ пластин из ФГМ. На рис. 7, а, приведены скорости 1-х мод ПАВ для пластин, представленных на рис. 6, а, c, e. На рис. 7, b, в более удобном формате показано поведение скоростей 1-й и 2-й мод ПАВ пластины m1–m3/m4 с приграничным расположением неоднородности (пунктирные линии, кривые 5, фрагмент рис. 6, e). На рис. 7, c, приведены скорости первых 3-х мод пластины m1–m3/m43–m4 (сплошные линии, кривые 3, фрагмент рис. 6, e). Рис. 7, d, представляет собой фрагмент рис. 7, c, для скоростей 2-й и 3-й мод в окрестности частоты к23. Для наглядности на рис. 7, c и d штриховой линией выделена 2-я мода SH-ПАВ.

Из рис. 7, а, видно, что при всех рассмотренных неоднородностях в пластинах из ФГМ, как и в пластине m1/m4, (кривая 0) происходит падение скорости от начального значения до V_G^I_B в случаях m1/m41–m4 (кривая 1), m1–m2/m42–m4 (кривая 2), m1–m2/m4 (кривая 4) и до минимального из значений VSe материалов пластины - vS^³) в случаях m1–m3/m43–m4 (кривая 3) и m1–m3/m4 (кривая 5).

Максимальное начальное значение скорости 1-й моды наблюдается в случае m1-m2/m4 (кривая 4).

Отметим особенности в поведении мод SH-ПАВ в пластинах с низкоскоростным включением. В случае m1/m41–m4 (кривая 1, рис. 7, а) с включением в ПМ-слое падение скорости 1-й моды происходит до значения V_F^min в низкочастотном диапазоне с последующим увеличением скорости до V_G^I_B . В случае m1–m3/m4 с локализацией неоднородности в ПЭ-слое у границы раздела (кривые 5, см. рис. 7, а, b), после падения скорости 1-й моды в низкочастотной области и дальнейшим ее возрастанием выделяется диапазон частот [ к0₅, к*₅], в котором скорость 1-й моды мало изменяется, находясь в окрестности значений VGIB. С увеличением частоты к₂> к*₅ скорость 1-й моды падает, выход на асимптотическое значение происходит на более высоких частотах.

Скорость 2-й моды, начиная с частоты ее зарождения, падает, выходя на значение VGIB при прохождении частоты к*5, в окрестности которой значения скоростей 1-й и 2-й мод достаточно близки. В случае m1–m3/m43–m4 с двумя низкоскоростными включениями у границы раздела слоев (кривые 3, см. рис. 7, а, c, d) кривая скорости 1-й моды претерпевает два изгиба в диапазоне низких и средних частот с последующим падением скорости до (m^)

значения V_Se³.

В поведении скорости 2-й моды в диапазоне частот ^к23, к23 ] выделяется «террасный» участок, на котором ее скорость мало отличается от V_G^I_B . После прохождении частоты к*23 скорость 2-й моды начинает падать. Поведение скорости 3-й моды повторяет поведение 2-й моды предыдущего случая: происходит падение скорости с выходом на значение V_G^I_B при прохождении частоты к^*₂₃ , в окрестности которой скорости 2-й и 3-й мод принимают близкие значения (см. рис. 7, c, d).

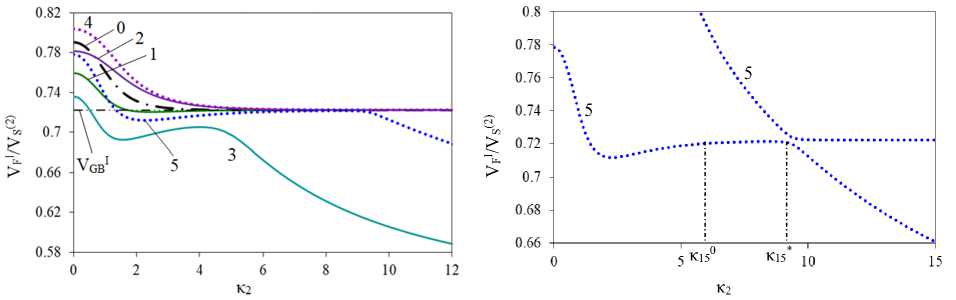
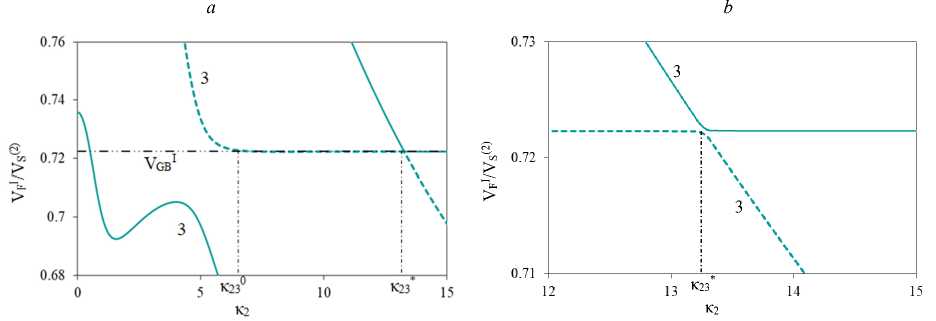
Рис. 7. Поведение скоростей первых мод SH-ПАВ в пластинах из ФГПЭМ/ФГПММ: а – поведение 1-х мод для пластин с рассмотренными неоднородностями; b – 1-я и 2-я моды, случай m1–m3/m4; c – 1-я, 2-я и 3-я моды, случай m1–m3/m43–m4; d – фрагмент (c)

Fig. 7. Behavior of the velocities of the first SH-SAW modes in FGPEM/FGPMM plates: a –behavior of the 1st modes for plates with the considered inhomogeneities; b – 1st and 2nd modes, case m1–m3/m4; c – 1st, 2nd and 3rd modes, case m1–m3/m43–m4; d – fragment (c)

Заключение

В работе в квазистатическом приближении исследованы особенности распространения SH-ПАВ в составной МЭУ-пластине из неоднородных ПЭ- и ПМ-слоев. При моделировании неоднородности слоев использована двухкомпонентная модель ФГМ с изменением свойств по толщине от значений параметров основного материала до значений параметров материала включения. В качестве основных материалов ПЭ- и ПМ-слоев пластины использованы PZT-5H (m1) и CoFe2O4 (m4). При выборе материалов включений ПЭ-слоя уделялось внимание материалам с незначительным различием значений упругих модулей при существенном отличии пьезоэлектрических и диэлектрических свойств. В предположении, что неоднородность ПМ-слоя связана с взаимопроникновением материалов слоев в узкой переходной области у границы раздела, параметры материалов включений выбирались близкими параметрам материала ПЭ-слоя и его включений. В рамках модели рассмотрено расположение включений ПЭ-слоя у поверхности пластины, в середине слоя и у границы раздела. Включения ПМ слоя локализованы у границы раздела. Волновой процесс в МЭУ-пластине из ФГПЭМ/ФГПММ инициирован действием