Особенности размещения и роста городов Южного федерального округа России

DOI:

Введение. В ходе реализации социальноэкономической политики в регионах возникает необходимость понимания процессов, вызывающих концентрацию ресурсов, населения, предприятий на конкретной территории. Это определяется тенденцией урбанизации, агломерационными факторами, усиливающими дифференциацию регионального развития в рамках страны. Проблема феномена размещения производительных сил в пространстве на современном этапе развития экономической науки является предметом систематических и активных исследований, что определено растущей дифференциацией социально-экономического состояния городов: в 2015 г. объем отгруженных товаров и услуг на душу населения в г. Москве составил 467 тыс. руб.; в г. Санкт-Петербурге – 421 тыс. руб.; в г. Белгороде – 414 тыс. руб.; в г. Краснодаре – 302 тыс. руб.; в г. Астрахани – 244 тыс. руб.; в г. Пензе – 147 тыс. руб.; в г. Майкопе – 56 тыс. руб.; в г. Махачкале – 15,4 тыс. рублей [10].

Доля прожиточного минимума в среднемесячной начисленной заработной плате в 2014 г. составляет: в г. Москве – 20 %; в г. Санкт-Петербурге – 19 %; в г. Белгороде – 23 %; в г. Астрахани – 22 %; в г. Краснодаре – 23 %; в г. Майкопе – 29 %; в г. Махачкале – 27 % [10].

Ученые пытаются объяснить концентрацию конкурентных преимуществ на одних территориях (трудовые ресурсы, инвестиции) и дефицит на других, в результате чего формируются города, ускоренного развития, опережающие территории, и растет межрегиональное неравенство. Таким образом, выявление особенностей размещения и роста городов в России является актуальным и своевременным исследованием.

Целью исследования, результаты которого отражены в данной статье, является выявление особенностей размещение и роста городов на территории Южного федерального округа России. В работе будут подтверждены или опровергнуты следующие гипотезы: 1) средняя численность населения города региона (за исключением столицы региона) коррелирует с расстоянием до ближайшего города-миллионника; 2) плотность населения в регионе имеет обратную зависимость с расстоянием до ближайшего города-миллионника; 3) темп роста численности населения коррелирует с объемом инвестиций в бюджет города.

Обзор исследований. Для достижения поставленной цели рассмотрим зарубежные и отечественные исследования по данной теме. Первой попыткой сформулировать гипотезу о регулярности городов и связи их с размером стала «теория центральных мест» В. Кристаллера, согласно которой города располагаются в иерархичном порядке в зависимости от размера (численность населения) [13]. Зарубежные исследователи стремятся объяснить, что вызывает пространственное неравенство. Р. Товнсенд, К. Уэда предлагают модель, которая определяет взаимосвязь между экономическим ростом, финансовой структурой и неравенством. Н.М. Абдель-Рахман моделирует социальное обеспечение и неравенство доходов в системе городов. Э. Глайзер выявляет экономические силы, способствующие росту городов в США [15], отмечая роль географии рынков и соседей в иерархии городов. Темп роста городов-соседей оказывает прямое влияние на социально-экономическую активность в городе.

М. Бекман утверждает, что в границах территории распределение по размеру города подчиняется правилу Парето с индексом, равным единице, данная закономерность получила название закона Ципфа [11], который заключается в том, что если крупные города ранжировать по убыванию численности их населения, то отношение численности двух городов будет обратно пропорционально отношению их рангов.

Т. Розен и М. Резник первыми провели комплексные исследования данного закона на примере 44 стран. Исследователи считают, что в Австралии индекс завышен, и относят этот случай к исключениям. Если убрать из выборки Австралию, то лидером по индексу Парето становится Нигерия – 1,5 [17]. Р. Харрисс в проводимых исследованиях доказал, что распределение размера городов требует учета влияния международных взаимосвязей на процесс экономического роста [18].

М. Раваллион утверждает, что урбанизация снижает численность населения сельской местности, но способствует росту городской бедности, увеличивает пространственные различия [16]. Среди зарубежных урбанистов в оценке городского роста популярностью пользуется закон Гиб-рата, согласно которого темпы роста населения города не зависят от его начального размера. В 1931 г. Р. Гибрат установил правило: пропорциональный темп роста фирмы не зависит от ее абсолютного размера [12]. Данный закон применим к городам.

Вопросами пространственного и городского неравенства в современной отечественной экономической науке занимаются О. Балаш (пространственное моделирование городов) [1]; А. Буфетова (тенденции развития системы «центр – периферия») [2]; К. Глущенко (оценка межрегионального неравенства) [3]; Ж. Зайон-чковская, Н. Ноздрина (миграционные потоки, радиус притягательности крупных городов на основе социологических исследований) [4]; Е. Коломак (неравномерность пространственного развития, городские агломерации) [5]; М. Малкина (неравенство региональных доходов) [6]; А. Трейвиш, Т. Нефедова (оценка состояния городов страны, прогнозирование их реакции на финансовый кризис) [7].

Методология исследования. Методологической базой послужил сравнительный анализ, метод группировок. Оценку стабильности городской системы Южного федерального округа проводили с использованием закона Ципфа. Закон Ципфа или Парето-распределение представляют собой выражение степенного закона. В эмпирической литературе для оценки экспоненты степенной функции используется метод наименьших квадратов. Его преимущество заключается в том, что он дает визуальные критерии согласно с законом (ф. 1):

In rank = A — K ln size , (1)

где ln _rank – логарифм ранга города; ln _size – численность населения города; K – параметр распределения, оценочный коэффициент Ципфа, который дает наклон линейной зависимости между размером города и городским рангом. Закон Ципфа соблюдается при условии K = 1, то есть самый большой город в к раз больше к -го по величине города. При К < 1 – размеры крупных городов больше прогнозируемых законом Ципфа; при К > 1 распределение городов более равномерно прогнозируемого законом Ципфа [14].

Для выявления особенностей роста городов по показателю численность населения – закон Гибрата , логарифмическая специфика которого представлена формулой (2):

In r , t = ^eo + Yln r , t - 1 , ⁽²⁾

где P₀— константа; r it — численность населения города i в год t ; r_{i, t –1} – численность населения города i в год t —1; если у 1 равен 1, то темп роста города и начальный размер независимы (закон Гибрата выполняется) [12].

В исследованиях, проведенных А. Чешером, установлены следующие характеристики коэффициента Y 1 :

• Y 1 < 1 — маленькие города растут быстрее, чем крупные;

• Y 1 > 1 — крупные города растут быстрее маленьких [12].

В таблице 1 представлены результаты анализа распределения городов России в границах федеральных округов, плотности и уровня урбанизации в федеральном округе.

Наибольшее количество городов расположено в Центральном федеральном округе, в Северо-Кавказском ФО – в 5,5 раз меньше. По численности городского населения лидером выступает ЦФО, а численность г. Москвы составляет 12 108 тыс. чел., следовательно, в 305 городах проживает 17 844 тыс. человек. Северо-Западный и Южный федеральные округа имеют одинаковую численность городского населения, но в СЗФО крупный город Санкт-Петербург с населением 5 132 тыс. чел., то есть на оставшиеся 146 городов приходится 8 711,7 тыс. чел., на территории СЗФО расположены в основном малые города.

Выявим основные закономерности размещения городов ЮФО (см. табл. 2).

Cогласно данным таблицы 2, на территории ЮФО в 2015 г. расположено два города-милли-

Таблица 1

Распределение городов на территории России в 2014 г.

Федеральный округ	Количество городов	Численность городского населения, тыс. чел.	Плотность населения, чел./км2	Уровень урбанизации, %
Центральный	306	29 952	59,9	81,8
Северо-Западный	147	13 843,7	8,2	83,9
Южный	79	13 963,8	33,3	62,8
Северо-Кавказский	56	9 590,1	56,7	49,1
Приволжский	198	19 672,7	28,7	71,2
Уральский	139	14 371,1	6,8	80,7
Сибирский	130	12 635,3	3,8	72,5
Дальневосточный	66	4 069,3	1,0	75,3

Примечание . Рассчитано авторами по: [10].

Таблица 2

Особенности городов Южного федерального округа, 2014 г.

Регионы	Количество городов	Численность населения, тыс. чел.		Уровень урбанизации, %	Плотность населения, 2 чел. на км	Расстояние до ближайшего города-миллионника, км
		столицы региона	оставшихся городов
Адыгея	2	145,5	12,5	35	57,3	333 (г. Ростов-на-Дону)
Астраханская область	6	530,9	111,1	63	20,7	424 (г. Волгоград)
Волгоградская область	19	1 018,0	798,0	71	22,8	424 (г. Волгоград)
Калмыкия	3	104,0	22,0	45	3,8	299 (г. Волгоград)
Краснодарский край	26	805,7	1 957,3	51	71,6	276 (г. Ростов-на-Дону)
Ростовская область	23	1 109,8	1 719,2	67	42,0	276 (г. Ростов-на-Дону)

Примечание . Рассчитано авторами по: [10].

онника: г. Волгоград, г. Ростов-на-Дону. Большая дифференциация численности населения городов имеет место в Астраханской, Волгоградской области и Республике Калмыкия, так как численность населения столиц данных регионов выше оставшейся части городского населения.

С применением закона Ципфа (правило «ранг – размер») проверим стабильность городской системы (по показателю численности городского населения) ЮФО в 2003–2014 гг. (см. рисунок).

Отметим, что в 2010 г. из состава ЮФО был выделен Северо-Кавказский федеральный округ, поэтому в анализе за 2003 г. учтены города СКФО. На рисунке показаны изменения в городской структуре обследуемого федерального округа в сторону увеличения стабильности, о чем свидетельствует график 2014 года.

Предположим, что данная ситуация является результатом исключения городов СКФО. Проверим заявленные гипотезы.

Средняя численность населения города региона коррелирует с расстоянием до ближайшего города-миллионника. Факторный признак –рассто-яние от города региона до города-миллионника, результативный – средний размер города региона (за исключением столицы). Показатели использовали по значению их натурального логарифма.

Базовая спецификация модели имеет следующий вид (ф. 3):

In y = 12 - 1,5ln x + £, (3)

где у – средний размер города региона (за исключением столицы), тыс. чел.; х – расстояние от города региона до города-миллионника, км; £ - ошибка.

Представленные результаты расчетов позволяют заключить, что размеры городов при удалении от городов-миллионников на 1 % уменьшаются на 1,5 %.

В результате проведенных расчетов вторая гипотеза не получила подтверждение.

Темп роста численности населения коррелирует с объемом инвестиций в бюджет города. Факторный признак – объем инвестиций в бюджет города, результативный – темп роста численности населения города. Анализ проводился за период 2009–2003 и 2014–2009 годов. Показатели использовали по значению их натурального логарифма.

За 2009–2003 гг. гипотеза не получила подтверждения. За период 2014–2009 гг. базовая спецификация модели имеет следующий вид (ф. 4):

In y = - 1,17 + 0,12 ln x + £ , (4)

где у – темп роста численности населения города; х – объем инвестиций в бюджет города, тыс. руб.; £ -ошибка.

В ЮФО увеличение объема инвестиций в бюджет города на 1 % способствует увеличению темпа роста численности населения на 0,12 %. Низкий коэффициент детерминации ( R ² = 0,28) объясняется неучтенными факторами влияния на зависимую переменную.

По условиям закона Гибрата, темпы роста города не зависят от его начального размера. Тестирование данного закона в системе городов ЮФО было проведено за период 2003– 2014 годов. Отметим, что для получения более объективных результатов целесообразно за

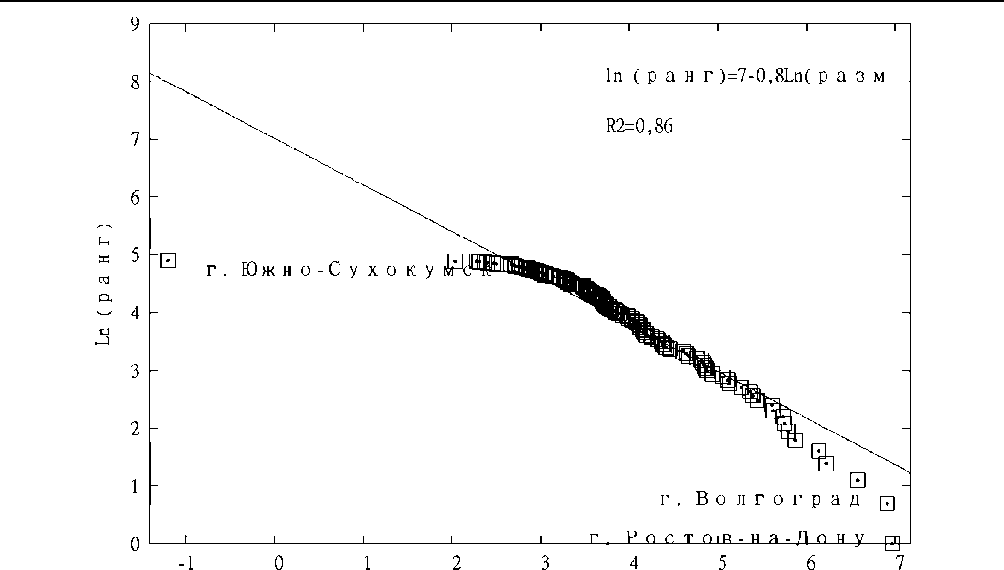
Ln( размер)

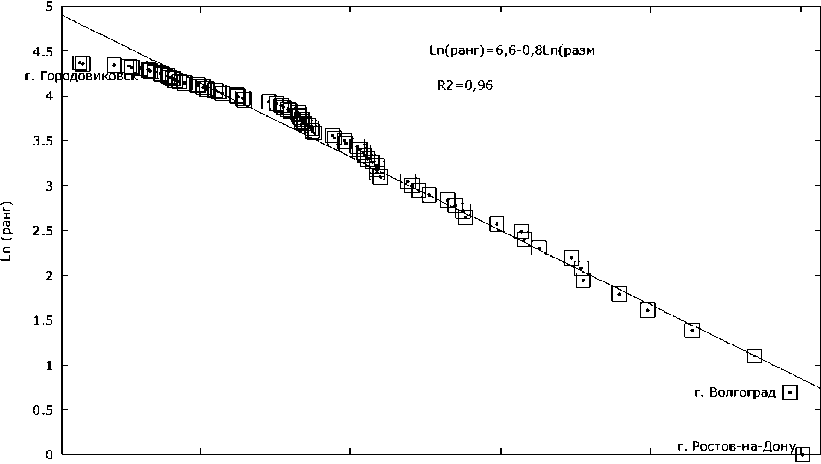
3                    4                    5                    6                    7

Ln (размер)

Рисунок. Зависимость «ранг – размер» по показателю численности населения для городов ЮФО Примечание . Рассчитано авторами по: [8; 10].

начальный период в анализе использовать данные года возникновения города, но в связи с низким уровнем развития муниципальной статистики РФ, получение таких данных затруднено, по большинству малых городов они отсутствуют.

Проведенные расчеты позволили получить следующие модели:

• 1)    период 2003–2009 гг. (ф. 5):

ln y, .=- 0,01 + 0,9ln x, ,                (5)

где y – численность населения города в 2009 г.; x – численность населения города в 2003 г.;

• 2)    период 2009–2014 гг. (ф. 6):

In y = 0,4 + 0,9ln x, ,                 (6)

где y – численность населения города в 2014 г.; x – численность населения города в 2009 г.

Таким образом, согласно коэффициента у 1 (коэффициент детерминации 0,9) на территории ЮФО в исследуемые периоды маленькие города растут быстрее крупных.

Рассмотрев особенности размещения и роста городов ЮФО, можно сделать ряд выводов:

• 1.    Размеры городов при удалении от городов-миллионников на 1 % уменьшаются на 1,5 %.

• 2.    Увеличение объема инвестиций в бюджет города на 1 % способствует увеличению темпа роста численности населения на 0,12 %.

• 3.    На территории ЮФО в 20014–2009 гг. маленькие города росли быстрее крупных.

• 4.    Теоретическая значимость проведенного исследования заключается в дополнении методологических основ оценки роста городов с использованием закона Гибрата по показателю численности населения.

• 5.    Полученные результаты могут быть использованы в деятельности региональных и муниципальных органов власти, позволят научно обосновать программы и стратегии социальноэкономического развития городов ЮФО.