Особенности синхронизации динамики численности в системе трех миграционно связанных популяций

И.Г. Суходоев, М.П. Кулаков, Е.В. Курилова, Е.Я. Фрисман Институт комплексного анализа региональных проблем ДВО РАН, ул. Шолом-Алейхема 4, г. Биробиджан, 679016, e-mail: , ; e-mail: , ; e-mail: , ; e-mail: ,

Одним из направлений изучения популяций и сообществ животных являются исследования динамики как отдельно взятых локальных групп особей, так и систем популяций, взаимодействующих между собой за счет миграции особей, которая может носить постоянный или сезонный характер. Необходимость рассматривать системы миграционно связанных популяций, образующих метапопуляцию, объясняется тем, что многие виды животных отличаются неравномерным распределением особей по ареалу. Это выражается в том, что на изучаемой территории имеется несколько связанных местообитаний, занятых особями одного биологического вида. Элементарным объектом изучения при этом является локальная популяция, которая может демонстрировать регулярную, периодическую или нерегулярную динамику.

При исследовании системы миграционно связанных популяций особое внимание уделяется изучению особенностей полной и фазовой синхронизации динамики между разными местообитаниями (участками). Давно известна роль синхронизации для сохранения и устойчивого развития миграционно связанных популяций на ареалах разного размера [7–9, 12, 13, 15, 17, 18]. В частности, в простейших моделях динамики метапопуляций показано, что полная синхронизация является тревожным симптомом [13], при котором катастрофическое снижение численности лишь на одном участке увеличивает риск полного вымирания на всем ареале [12]. С другой стороны, показано, что переход от полной синхронизации к противофазной глобально стабилизирует динамику системы равновеликих и симметрично связанных популяций за счет расширения бассейнов притяжения противофазных режимов [7, 8, 15, 17, 18].

Существует несколько подходов к изучению синхронизации динамики связанных популяций с применением дифференциальных или разностных уравнений, описывающих процессы с непрерывным или дискретным временем. Обычно используются либо качественные методы, связанные с анализом устойчивости состояний равновесия, либо методы численного анализа, сопровождаемые проведением большого числа экспериментов и количественным анализом режимов динамики. В последнем случае на основе методов исследования связанных отображений (или связанных осцилляторов), а также различных показателей коллективной динамики количественно идентифицируется тип динамического поведения [1].

Отметим, что с биологической точки зрения несколько слабо связанных популяций одного вида, имеющих синхронную или синфазную динамику, могут быть приняты за одну большую популяцию (кластер), а несинхронные им – как популяции меньшего размера. Вместе с тем незначительное изменение силы связи может привести к возникновению противофазных колебаний численностей локальных популяций или частичной синхронизации [6].

Исследование поведения диссипативно связанных автоколебательных осцилляторов является фундаментальной задачей теории колебаний и нелинейной динамики [1, 3, 10]. Так, А.П. Кузнецов в своей работе [2] описал динамику трех связанных генераторов, способных демонстрировать автономные квазипериодические колебания, и провел сравнение полученных результатов со случаем трех связанных осцилляторов Ван дер Поля.

В работе [1] при рассмотрении цепочки трех диссипативно связанных автоколебательных осцилляторов с неидентичными управляющими параметрами показана возможность возникновения как полной синхронизации осцилляторов, двух- и трехчастотной квазипериодичности, так и полной широкополосной синхронизации, возникающей при сколь угодно большой величине частотной расстройки [16].

В последнее время особое внимание уделяется задаче о трех- (и более) частотной синхронизации [4, 5] в контексте феномена синхронизации квазипериодических колебаний. Так, в [5] рассмотрена динамика цепочки трех идентичных осцилляторов [1]. В работе [11] исследуются механизмы появления и исчезновения режимов полной синхронизации хаоса в кольце из трех логистических отображений с симметричной диссипативной связью, рассматриваются типичные колебательные режимы и переходы между ними. Исследованы некоторые механизмы формирования кластеров синхронных популяций в цепочке из большого числа миграционно связанных популяций [6].

Данная работа развивает подходы и методы исследования систем связанных популяций. Рассматривается кольцевая система из трех миграци-онно связанных популяций с непересекающимися поколениями, которая описывается моделью с дискретным временем. Исследуются особенности динамики и условия фазовой синхронизации циклов разных периодов (длин) в зависимости от параметров роста и силы связи. Отметим, что подобная модель для двух связанных популяций, динамика которых описывается уравнением Ферхюльста, была исследована ранее в [7]. Можно ожидать наследования части свойств динамики, обусловленных синхронизацией и мультистабильностью, а также появления новых эффектов, невозможных для двух популяций.

Модель динамики численности трех миграционно связанных популяций Рассмотрим случай, когда на некоторой территории существует три локальных популяции (субпопуляции), заселяющие сопредельные местообитания и связанные миграцией особей. Объектом моделирования могут выступать обособленные группы животных (стада, стаи), изолированные друг от друга и совершающие сезонные миграции между тремя участками.

В этом случае взаимодействие трех популяций может быть схематично изображено в виде графа с замкнутыми вершинами (цикла), показанного на рис. 1. Обозначим через x, y и z численно- сти популяций на первом, втором и третьем участках соответственно. Стрелки на рис. 1 указывают направления перемещения особей, а коэффициенты mij (где i, j=1, 2, 3) обозначают долю особей, перемещающихся из i-й популяции в j-ю. Интенсивность таких миграций определяется численностью той субпопуляции, откуда и куда происходят миграции.

ный доле от численности каждой популяции после размножения, которые пополняют два связанных с ней участка. Функция f(x) описывает локальный рост популяции со следующими свойствами: f(0)=a и df/dx<0, где a – максимальная скорость роста популяции. Такой вид функции позволяет описать плотностную регуляцию численности: максимальный рост наблюдается при низкой чис- ленности, когда внутривидовая конкуренция за

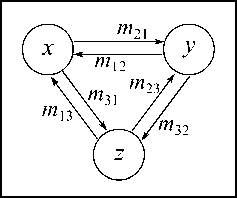
Рис. 1. Схематическое изображение системы трех миграционно связанных популяций

Fig. 1. Scheme of interaction of three populations coupled by migration

В дальнейшем будем рассматривать случай полной идентичности субпопуляций с симметричным характером миграционного взаимодействия. То есть предполагается, что скорости роста и число особей, покинувших популяцию (иммигрантов) и пришедших в нее (эмигрантов), имеют сходные значения ( m_ij = m ), а условия проживания для всех трех популяций являются одинаковыми.

Будем считать, что воспроизводство носит сезонный характер, а миграция осуществляется в промежутках между сезонными размножениями, причем расселение происходит после периода размножения и носит диссипативный характер. Такой характер связи предполагает, что эмигранты становятся неотличимыми от местных особей и сразу принимают участие в размножении, что влияет на мгновенную численность особей, сглаживает различия численностей и характер локальной динамики.

Таким образом, уравнения динамики численности трех миграционно связанных популяций имеют вид:

' x n + 1 = f ( x n X¹ - ² m ^{) +} m ( f ( У п ) ⁺ f ( z n ))’

< Уп + 1 = f(Уп )(1 - 2m) + m(f(xn ) + f(znU (1) _zn+1 = f(zn X1 - 2m) + m(f(xn ) + f(Уп ft где xn, yn и zn – численности в n-й сезон размножения, m – коэффициент миграции (0≤m≤0.5), рав- ресурсы минимальна, а с ростом численности кон- куренция усиливается и рост замедляется.

Рассмотрим функцию f в виде дискретного аналога модели Ферхюльста, т.е. f(xn)=axn(1–xn/K), где K – экологическая ниша популяции. Путем несложной замены переменных Kxn→xn, Kyn→yn, Kzn→zn от уравнений (1) можно перейти к модели с относительными численностями:

'x n + 1 = ^ax n ^{( 1} - x n X¹ - ² m ^{) +}

⁺ am ⁽ У п ^{( 1} - У п ^{) +} z n ^{( 1} - z n ft ^ У п + 1 = ^аУ п ^{( 1} - У п X¹ - ² m ^{) +}

⁺ am ⁽ x n ⁽ 1 - x n ⁾⁺ z n ^{( 1} - zn ft z n + 1 = az n ^{( 1} - z n X¹ - ² m ^{) +}

+ am ⁽ x n ^{( 1} - x n ⁾⁺ У п ^{( 1} - У п ft

Система (2) имеет

тривиаль-

ную x 0 = у 0 = = z 0 = 0 и нетривиальную X 1 = у 1 = Z 1 = ( a - 1)/ a = h особые точки. Очевидно, что условия их устойчивости аналогичны условиями одномерного уравнения x_{n+ 1}= ax_n (1– x_n/K ): тривиальная точка устойчива при 0< a <1, нетривиальная при 1< a <3. Потеря устойчивости ненулевой точки происходит согласно каскаду удвоения периода, в результате которого при 3< a ≤4 динамика демонстрирует пилообразные колебания численности (циклы), подчиняющиеся универсальности Фейгенбаума.

Наличие трех связанных популяций с циклами одного периода приводит к тому, что из-за различий в начальных значениях пики численностей могут изначально не совпадать, т.е. не совпадают фазы колебаний. Однако при определенных условиях миграция способна «сблизить» и синхронизировать эти колебания, даже в случае слабой связи. Либо несинхронные режимы окажутся устойчивыми и будут наблюдаться неограниченно долго (при n→∞ и m>0). Под несинхронными режимами будем понимать такие режимы динамики двух или более популяций, периоды или фазы колебаний которых не совпадают. Более строго, если argmin supxn - Уп+J| = 0

0 < о < О при n→∞ (T – максимальный для xn и yn период колебаний), то динамика фазовых переменных x и y синхронная (синфазная). Если argmin sup|x„ - yn+r|> 0

0 < о <  О

^, то несинхронная (несинфазная).

Вместе с тем давно известно, что в системах разного числа связанных отображений полностью синхронные режимы (| x_n – y_n |=0 при n →∞), для которых совпадают фазы и периоды циклов, могут сосуществовать с несинхронными режимами, когда нет совпадения фаз или периодов. В этом случае говорят о фазовой мультистабильности режимов динамики, при которой в зависимости от начальных условий в системе (2) в асимптотическом случае возможно несколько режимов, отличающихся фазами колебаний переменных x_n , y_n и z_n относительно друг друга (с разными значениями τ ).

Для системы двух связанных отображений хорошо известно, что синхронные режимы всегда рождаются в результате первого удвоения периода неподвижной точки, т.е. при a >3 [7, 8, 10, 15, 17]. Граница существования и устойчивости несинхронных режимов зависит от коэффициента миграции m , а при m =0 она, очевидно, совпадает с границей a =3 для синхронных режимов. С ростом m несинхронные режимы возможны при более высоких значениях a . Можно ожидать, что аналогичный сценарий наблюдается в системе (2).

Очевидно, что в системе трех связанных популяций, демонстрирующих колебания с периодом 2 (2-цикл), возможно две ситуации: синхронны все три популяции или лишь две, а третья несинхронная (несинфазная) с ними. Несинхронную динамику сразу трех популяций можно ожидать для циклов больших периодов, например, 3-цикла.

Рассмотрим условия формирования несинхронных режимов на примере 2- и 3-цикла.

Формирование синхронных и несинхронных режимов

Для исследования качественных перестроек (бифуркаций) в системе (2) построим одномерную буфуркационную диаграмму при изменении параметра a и фиксированном значении m. Для этого будем изменять величину a в допустимом диапазоне (для системы (2) 10: ai=a0+Δi (i=0,1,2,…). Для каждого ai строится 5000 итераций уравнений (2) и 200 последних помещаются на координатную плоскость (a, x), (a, y) или (a, z). Если при этом несколько элементов последовательности {(xn, yn, zn), n=4801,4802,…,5000} имеют достаточно близкие значения, то соответствующие точки сольются и на диаграмме останется небольшая их часть. Ко- личество оставшихся точек для фиксированного ai указывает на период колебаний (длину цикла). Если элементы (xn, yn, zn) образуют плотное облако точек, то можно говорить о сложном нерегулярном поведении. Отметим, что модель (2) демонстрирует мультистабильность, когда выбор начальной точки существенно влияет на характер и синхронизацию динамики переменных xn, yn и zn. Озвученная классическая процедура построения буфуркационных диаграмм обычно выполняется двумя способами: для каждого значения ai стартовая точка (x0, y0, z0) фиксирована (построение бу-фуркационной диаграммы без наследования) или изменяется, когда она является последней точкой исследуемой системы для предыдущего значения ai-1 (с наследованием).

Построим буфуркационные диаграммы двумя указанными способами. На рис. 2 a изображено две совмещенных диаграммы с наследованием (красные точки) и без наследования (синие точки). По диаграмме видно, что при a = 2.8 нетривиальная неподвижная точки системы (2) устойчива до a = 3. В данном случае с ростом параметра a и при наследовании стартовой точки, по сути, прослеживается каскад удвоения периода только синхронных режимов, который, очевидно, аналогичен каскаду в одномерном уравнении: x_{n+ 1}= ax_n (1– x_n ). Поскольку уже при a = 2.8 траектория модели достигает равных значений фазовых переменных ( a –1)/ a , следующая стартовая точка даже для a > 3 может привести только к синхронным режимам ( x_n = y_n = z_n ).

В процедуре без наследования начальная точка подбирается таким образом, чтобы обеспечить несинхронную динамику для тех значений a , для которых она возможна. Однако в области параметров, где возможны лишь синхронные режимы, траектория неизбежно сходится к синхронному режиму (поскольку других нет), и синие точки сливаются с красными. Вместе с тем после некоторого критического значения a в модели происходит ряд качественных перестроек и траектория все же достигает устойчивого несинфазного режима, а на диаграмме в стороне от красных точек наблюдаются синие, соответствующие несинфазному поведению двух популяций (рис. 2 a ). Несложно заметить, что такие режимы появляются довольно жестко, а их последующие бифуркации происходят позже (при более высоких значениях a ), чем для синхронных режимов. Кроме того, увеличение коэффициента миграции m еще дальше отодвигает точки бифуркаций синфазных и не-

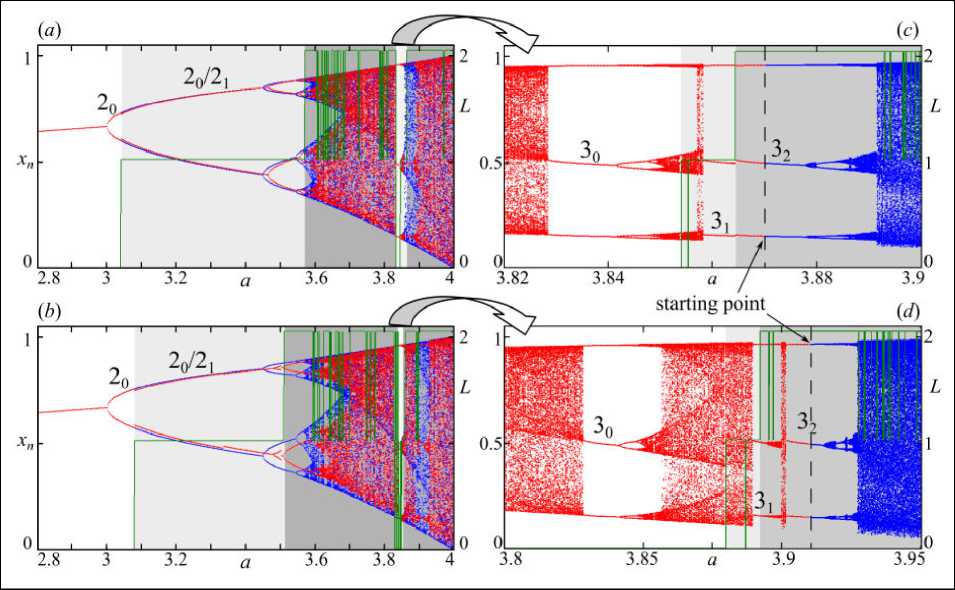
Рис. 2. Бифуркацонные диаграммы системы (2) при вариации параметра a и следующих начальных значениях: (a)-(b) x0= 0.99, y0= 0.5, z0= 0.15, m = 0.005 и (c)-(d) x0 = 0.49, y0 = 0.96, z0 = 0.15, m = 0.01. Красная и синяя линии – предельные значения xn при разных начальных условиях, зеленая линия – величина L, характеризующая степень взаимной фазовой синхронизации

Fig. 2. Bifurcation diagrams of system (2) at variation of parameter a, and the following initial values: (a)-(b) x0=0.99, y0=0.5, z0=0.15, m=0.005 and (c)-(d) x0=0.49, y0=0.96, z0=0.15, m=0.01.

The red and blue lines are the limiting values of xn for different initial conditions; the green line is the value of L, which characterizes the degree of mutual phase synchronization. The red and blue lines are the limiting values of xn under different initial conditions; the green line is the value of L, which characterizes the degree of phase synchronization синфазных режимов, и, по всей видимости, меняет тип их бифуркаций (рис. 2b).

Для идентификации синфазных и несинфазных режимов воспользуемся данным выше определением для этих типов динамики. Рассмотрим неотрицательные величины

L 1 = argmin ^s up|| x , - У п _{+ r} || , L 2 = argmin ^s up| x - z n ₊ J|

0< о < О                              0< о < О и L3 = argmin sup||Уп - zn + r || .

0 < о <  О

Несложно понять, что если переменные xn, yn и zn попарно синхронны (синфазны) между собой, то эти три величины одновременно равны нулю, т.е. L1+L2+L3= 0. Если синхронны лишь две переменные, то нулю будет равна только одна из этих величин, т.е. L1L2= 0 или L1L3= 0, или L1L3= 0. Если все три переменные не синхронны, то эти величины будут больше нуля, т.е. L1L2L3>0. Тогда введем величину L, которая характеризует степень взаимной фазовой синхронизации трех переменных. Она принимает три значения – 0, 1 или 2 – в каждом из перечисленных случаев.

На рис. 2 зеленая линия показывает то, как изменяется величина L для режимов, отмеченных на бифуркационной диаграмме, т.е. для элементов последовательности {(xn, yn, zn), n=4801,4802,…,5000} при конкретном ai. Ясно, что для первой диаграммы с наследованием (красная линия), которая стартует из точки a=2.8, возможны только синхронные режимы и L=0. Для диаграммы без наследования (синяя линия) для некоторых ai и при фиксированной стартовой точке траектория системы (2) выходит на частично синхронный режим с двумя синфазными и одной несинфазной переменной, тогда L=1. Из графи- ка величины L видно, что после некоторого ai в системе (2) возникает несинхронный режим на основе колебаний с периодом 4, 8, 16 и т.д., для которых несинфазными могут оказаться все три переменные, тогда L=2. Кроме того, видно, что хаотическая динамика в целом представлена несинхронными режимами (L=2) с редкими переходами к частичной (L=1) и полной синхронизации (L=0) в окнах периодичности (3-цикл, 5-цикл и др.).

На рис. 3 приведены примеры динамики численности трех связанных популяций, описываемых системой (2). Для обозначения формируемых циклов используется следующая нотация: TL – цикл длины T (период), L – показатель взаимной фазовой синхронизации переменных, рассчитываемый по вышеуказанной методике. Например, 20 – синфазные колебания трех популяций с периодом 2, 21 – синфазны только две популяции из трех. Из приведенных примеров видно, что 2-цикл имеет только два этих варианта, а вариант с колебаниями трех популяций с разными фазами возможен только для циклов больших периодов, например, для 8-цикла (последний график на рис. 3a) или 3-цикла (рис. 3b). На рис. 3 показано, что при низких значениях скорости роста a траектория быстро выходит на устойчивый режим (рис. 3a). При высоких же значениях a для выхо- да на устойчивый аттрактор траектории требуется длительное время, поскольку начальная точка выбиралась достаточно произвольно.

Несложно понять, что циклом с минимальным периодом, при котором динамика трех популяций может быть несинхронной (при L =2), является 3-цикл. Для изучения данного режима в качестве начального значения параметра a ₀ подберем такое его значение, при котором наблюдается 3-цикл, а динамика трех популяций изначально будет несинхронной. Построим диаграмму с наследованием как в сторону роста параметра a , т.е. a_i=a ₀ +hi ( i =0, 1, 2,…), так и его снижения, т.е. a_i=a ₀ –hi ( i =0, 1, 2,…). На рис. 2 c и d стрелкой отмечена данная стартовая точка, а цвет указывает на разное направление варьирования параметра a . Такой подход позволит проследить эволюцию изучаемого режима от его зарождения (слева), до разрушения (справа) в области нерегулярной динамики.

На рис. 2 c приведен фрагмент бифуркационной диаграммы, где показана эволюция 3-цикла. Согласно порядку Шарковского с ростом бифуркационного параметра a происходит «разрушение» хаотического режима, из которого рождается устойчивый 3-цикл, изначально представленный только синфазным поведением трех популяций (3₀). Далее это цикл испытывает каскад удвоений

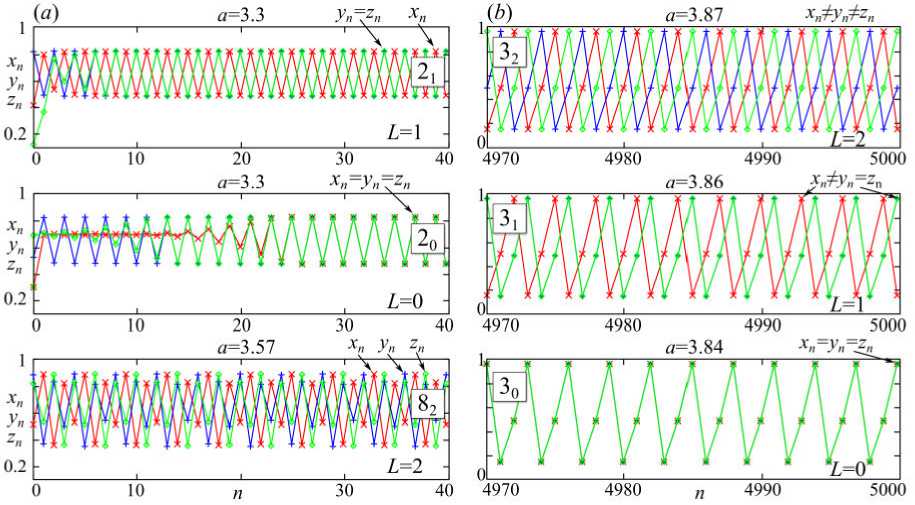
Рис. 3. Примеры динамики системы (2) при m=0.005: (a) 2- и 8-цикл, (b) 3-цикл. Значения параметра a приведены над графиками

Fig. 3. Examples of the system (2) dynamics at m=0.005: (a) 2- and 8-cycle, (b) 3-cycle. The values of the parameter a are given above the graphs

периода, оканчивающийся хаотическим, но синхронным поведением трех популяций на прямой x = y = z . Следом, в зависимости от коэффициента миграции m , появляется хаотический или периодический режим с синфазным поведением двух популяций (3₁). Очевидно, что он представлен тремя вариантами (на плоскости x = y или x = z , или y = z ), которые могут сосуществовать с синхронным режимом. Однако после некоторого критического значения a область притяжения (бассейн) синхронных режимов стягивается к линии x = y = z с мерой нуль, и синхронизация по факту невозможна. Дальнейший рост a приводит к определенной серии бифуркаций, непохожих на качественные изменения синхронных режимов. По всей видимости, в фазовом пространстве вокруг каждого элемента частично синхронного 3-цикла (периодическая точка с периодом 3) рождаются предельные инвариантные кривые, расположенные в плоскостях x = y или x = z , или y = z . Разрушение этих кривых приводит к полной потере фазовой синхронизации и рождению режима с тремя несинфазными популяциями. Бифуркация такого режима происходит также через образования трех предельных инвариантных кривых вокруг элементов несинфазного 3-цикла.

В зависимости от значения параметра m три варианта фазовой синхронизации циклов любой длины могут сосуществовать и иметь в фазовом пространстве свои области притяжения (бассейны). Для трехмерных динамических систем их построение является нетривиальной задачей, сопряженной с перебором начальных условий и анализом возникающих режимов динамики, а также визуальным представлением трехмерных бассейнов. Однако анализ только устойчивых режимов не дает полного представления о механизмах и условиях формирования режимов динамики с разной степенью фазовой синхронизации. Наиболее полное представление можно получить из анализа фазовых портретов, которые включают описание глобального поведения при движении траектории от одной неподвижной или периодической точки к другой, с выделением сепаратрисных поверхностей, отделяющих области притяжения разных режимов.

Далее мы рассмотрим построение полного фазового портрета одного из динамических режимов модели, а именно 2-цикла.

Полный фазовый потрет и глобальная динамика

Выберем параметры модели (2), соответствующие устоявшейся динамике с периодом 2

(2-цикл), которая реализуется двумя способами: все популяции синхронны между собой (2₀), синхронны только две из них, а третья синфазна им (2₁ ). Например, такое наблюдается при a =3.4 и m= 0.01 (рис. 2). Для построения полного фазового портрета в этом случае необходимо найти все неподвижные и периодические точки, оценить тип их устойчивости и максимально полно описать характер динамики при движении от одной точки к другой. Для этого необходимо описать движение вдоль некоторых особых направлений – многообразий, возмущения которых соответствуют траекториям модели (2).

Отметим, что знание о структуре фазового пространства позволяет увидеть всевозможные типы динамики численностей связанных популяций, включая переходные процессы, которые обычно «опускаются» при традиционном анализе устойчивости. Кроме того, полный фазовый портрет позволяет в деталях проследить за бифуркациями, приводящими к появлению устойчивых периодических решений, которые сосуществуют с неустойчивыми или седловыми состояниями. Последние определяют геометрию бассейнов притяжения и оказывают влияние на характер динамики.

Как известно, в окрестности неустойчивой неподвижной точки существует локальное неустойчивое многообразие, которое касается собственных подпространств, задаваемых собственными векторами якобиана системы. Локальное многообразие можно продолжить до глобального устойчивого W^S или неустойчивого W^U , двигаясь малыми шагами вдоль траектории исследуемой системы в прямом и обратном времени [19].

Для построения многообразий воспользуемся алгоритмом, предложенным в статье [14]. Аппроксимация многообразия стартует из неподвижной точки и ее возмущения вдоль собственных векторов. Несложно убедиться, что система (2) имеет следующие собственные числа: λ1= a–2 и λ2,3= (a–2)(1–3m). Первому числу соответствует единичный собственный вектор e1= (1,11)T. Движение вдоль него определяет полностью синхронную динамику трех переменных. Тогда отрезок, соединяющий неподвижную и периодическую точку с синхронной динамикой, совпадает с неустойчивым многообразием для синхронных режимов. Кратным же собственным числам λ2,3 соответствует система собственных векторов, натянутых на линейное трехмерное пространство. Например, можно указать два вектора: e2= (–1,1,0)T и e3= (–1,0,1)T, для которых верно: Je2,3= λe2,3. Но более важно, что это равенство верно для любой линейной комбинации e2 и e3, т.е. J(α2e2 + α3e3) = =λ2,3(α2e2 + α3e3), где α2,3∊R. В дополнение к указанным векторам рассмотрим следующий набор векторов, ортогональных единичному вектору: (1,1,–2)T, (1,–2,1)T, (–2,1,1)T и (0,1,–1)T, а также противоположные им. Поскольку λ1< –1 при a = 3.4, то система (2) задает неориентированное отображение. Поэтому при построении многообразия необходимо вычислять вторую итерацию (т.е. рассматривать значения x2n, y2n, и z2n), а вместе с каждым собственным вектором рассматривать противоположный ему вектор.

На рис. 4a. показано 12 одномерных многообразий, которые стартуют из этих наборов векторов (касаются их). Несложно заметить, что часть из них заканчивается в устойчивых перио- дических точках, а часть проходит в окрестности седло-фокусов. Если при построении этих кривых не вносить никаких возмущений и вычисления производить максимально аккуратно, то многообразие, стартующее из неустойчивой неподвижной точки, закончится в седло-фокусе и будет невозможно оценить характер динамики в ее окрестности и продолжить многообразие в сторону устойчивой точки. Поэтому будем немного возмущать стартовую точку вектором ± εe1 (ε > 0 – достаточно малое). В результате вычисленная кривая будет максимально близка к истинному многообразию, но при этом будет отдаляться от него в окрестности седло-фокуса. Двигаясь вдоль этих кривых, несложно оценить тип устойчивости точек без необходимости точного вычисления их координат. Например, если кривая WU «обрывается» в неко-

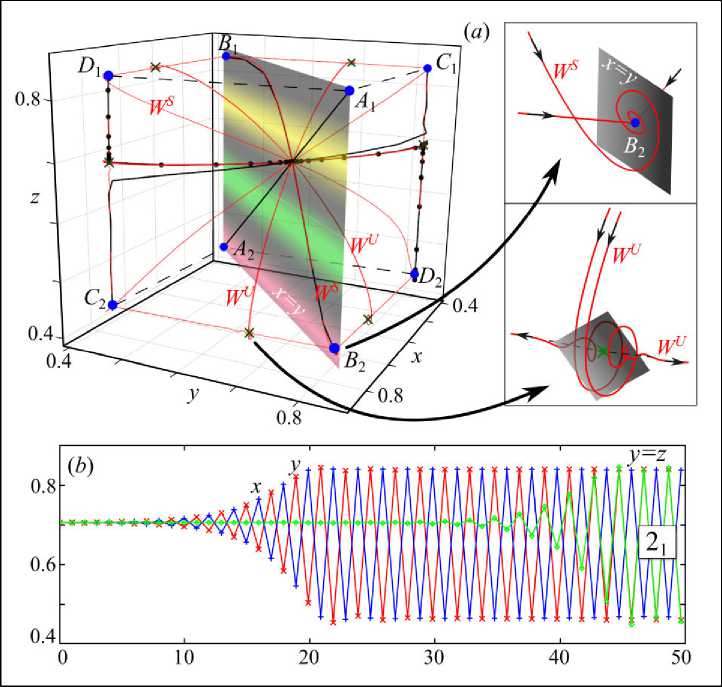
Рис. 4. (a) Фазовый потрет системы (2) при a=3.4 и m=0.005, а также увеличенные его фрагменты в окрестности устойчивой (B2) и неустойчивой периодической точки (обозначена крестиком). (b) Пример динамики в случае движения траектории вдоль неустойчивого одномерного многообразия WU

Fig. 4. (a) Phase portrait of system (2) at a=3.4 and m=0.005, as well as its enlarged fragments in the neighborhood of the stable (B2) and unstable periodic point (showed by a cross). (b) Example of dynamics with a trajectory moving along an unstable one-dimensional manifold WU

торой точке, то она, вероятно, устойчивая. Если W^U подходит к точке, а затем отдаляется от нее, то точка неустойчивая или седловая. Если кривая закручивается в спираль в ее окрестности, то можно говорить о фокусе. Дополнительно несложно вычислить решения системы (2), которые будут проходить в окрестности многообразий. На рис. 4 a аппроксимация многообразий показана красным цветом, а решения системы показаны черным, которые дополнены графиком динамики переменных x_n , y_n и z_n (рис. 4 b ).

Таким образом, был получен набор траекторий, которые достаточно близки к искомым устойчивым и неустойчивым одномерным многообразиям, подробно описывают набор всех периодических точек (включая неподвижную), характер их устойчивости, а также подробно характеризуют глобальную динамику (рис. 4 a ).

Несложно заметить, что точки, соответствующие элементам 2-цикла, с разной степенью фазовой синхронизации лежат в противоположных вершинах параллелепипеда (на концах главных диагоналей). На рис. 4 a пара точек, соответствующая полностью синхронным колебаниям (2₀), обозначена буквами A ₁ и A ₂. Ясно, что они лежат на отрезке биссектрисы первого квадранта ( x = y = z ). Три другие пары точек, обозначенные как B _1,2, C _1,2 и D _1,2, лежат в плоскостях x = y , x = z и y = z и соответствуют синхронному поведению лишь двух популяций (2₁). На ребрах между точек, соответствующих частично синхронной динамике (2₁), расположены точки типа седло-фокус, которые обозначены крестиком. Из построенного таким образом фазового портрета становится ясно, почему невозможно асинхронное поведение трех популяций на основе 2-цикла.

Снизу справа на рис. 4 a показан увеличенный фрагмент кривой W^U , которая закручивается в спираль, приближаясь к неустойчивой точке, а затем движется влево или вправо в зависимости от направления начального возмущения. Очевидно, что данная седловая точка и формируемое в ее окрестности двумерное неустойчивое многообразие (его фрагмент показан серым прямоугольником) задают сепаратрисную поверхность, которая соответствует границе бассейнов притяжения разных режимов. Если начальная точка лежит справа от нее, то траектория сойдется к паре точке B _1,2; если слева, то к паре C _1,2. Аналогичным образом фазовое пространство делится между бассейнами точек C _1,2 и D _1,2, B _1,2 и D _1,2.

В то же время, приближаясь к устойчивой периодической точке, траектория либо достигает ее под острым углом, либо закручивается в спираль в ее окрестности (сверху справа на рис. 4a). Это, в частности, указывает на то, что дальнейшие бифуркации 2-цикла могут идти по сценарию Неймарка-Сакера и сопряжены с образованием предельных инвариантных кривых.

На рис. 4 b показано решение системы (2), которому на рис. 4 a соответствуют черные кружки на черной линии. В данном примере из-за наличия седло-фокуса и сепаратрисной поверхности траектория, стартующая из окрестности неподвижной точки, сойдется к какому-то одному режиму в зависимости от малых возмущений. Однако прежде, чем это произойдет, траектория неизбежно пройдет в окрестности седло-фокуса. До этого момента динамика численности одной из популяций долгое время не будет испытывать колебаний, в то время как две другие будут противофазны друг другу. Это соответствует ситуации, когда одна популяция «зажата» между двумя другими. В результате противофазные колебания численностей «интерферируют» в ней и популяция продолжительное время не испытывает колебаний. Однако такое состояние с тремя несинхронными популяциями неустойчивое, поэтому «зажатая» популяция неизбежно синхронизируется с одной из популяций.

Отметим, что исследование синхронизации 3-цикла через конструирование многообразий и построение фазового портрета – это довольно нетривиальная задача. Ее сложность связана с тем, что 3-цикл появляется в результате разрушения хаоса. В этом случае в фазовом пространстве существует счетное множество неустойчивых точек, оставшихся в результате каскада удвоения периода. В результате инвариантные многообразия имеют сложную структуру и нетривиальным образом соединены между собой. Без сомнения, это требует дальнейшего детального исследования.

Выводы

Проведенное исследование системы трех миграционно связанных популяций позволяет заключить, что колебания численностей (циклы) демонстрируют фазовую мультистабильность. В этом случае в зависимости от начальных численностей формируются либо синхронные циклы, либо режимы, отличающиеся степенью фазовой синхронизации на смежных участках.

Показано, что 2-цикл помимо полностью синхронного варианта динамики трех популяций может иметь три варианта с двумя синхронными (синфазными) и одной несинхронной (несинфазной) им популяцией. В это время для циклов боль- ших длин, в том числе 3-цикла, динамика трех популяций может иметь сдвиг фазы колебаний (быть несинхронной). На примере 2- и 3-цикла показано, что при вариации скорости роста и коэффициента миграции происходит переход от состояния, когда возможна только синхронная динамика, к состоянию с двумя, а далее тремя несинхронными популяциями. В случае 2-цикла крайний вариант возможен только как часть переходной динамики.

Исследовано устройство фазового пространства в случае 2-цикла. Обнаружено, что каждая периодическая точка, соответствующая разным вариантам фазовой синхронизации, окружена набором седловых точек, которые задают бассейны притяжения разных вариантов совместной динамики. Можно предположить, что характер бифуркаций, приводящих к появлению этих точек, и, соответственно, сценарий усложнения динамики значительно отличаются от системы двух связанных популяций. Отметим, что несинхронная (несинфазная) динамика, наблюдаемая для трех популяций на основе 3-цикла, по всей видимости, возможна для трех и более популяций. Такой режим примечателен тем, что его можно представить как сдвиг одного и тоже пика численности при движении особей по кругу. Примечательно, что это происходит в системе симметрично связанных популяций. Поэтому его исследование, например, методом фазовых портретов, предложенным в статье, имеет довольно заманчивые перспективы.

Работа выполнена в рамках государственного задания Института комплексного анализа региональных проблем ДВО РАН.