Особенности статистического распределения разности фаз в спекл-поле: численный и натурный эксперименты

Рассеяние лазерного (когерентного) света случайно неоднородным объектом сопровождается формированием дифракционного спекл-модулированного оптического поля [1–4]. Такие поля имеют место при записи оптических голограмм объектов с рассеивающими поверхностями [5–7], в методах спекл-фотографии [3, 4, 7], в лазерной интерферометрии диффузно рассеивающих объектов и сред [4, 7, 8], в методах спекл-интерферометрии в оптической астрономии [9–11], в формировании образа объекта в механизме зрительного восприятия человека [12], в лазерных сканирующих системах формирования изображения [13, 14] и во многих других оптических методах и системах, где происходит рассеяние когерентных пучков света.

Статистические свойства спекл-модулированного поля, в частности, его фазовые статистические закономерности, проявляются в интерференционных эффектах с участием таких полей. При достаточно глубокой пространственной фазовой модуляции оптического поля в актах рассеяния, когда пространственные флуктуации фазы достигают 2π радиан, формируется так называемое развитое спекл-поле. Согласно [1, 2], комплексная амплитуда развитого спекл-поля в произвольной точке пространства имеет Гауссову статистику, а начальная фаза колебаний имеет равномерную плотность распределения вероятности в основном интервале [0,2π]. Эти представления переносятся и на статистические свойства разности фаз колебаний в различных спеклах дифракционного поля. Полагается, что при переходе от одного спекла к соседнему фаза поля также должна равновероятно изменяться в интервале [0,2π]. В общем случае для источников рассеянного когерентного поля с апертурой произвольной формы, как показали наши эксперименты, такое представление вполне оправдано. Однако в работах [15–20] показано, что в случае δ-коррелированного источника, распределение средней интенсивности по апертуре которого описывается чётной функцией координат, случайная составляющая модуля разности фаз в различных точках спекл- поля в дальней зоне дифракции с наибольшей вероятностью принимает два значения - 0 и π радиан.

Экспериментальное подтверждение данного обстоятельства получено путём прямых измерений разности фаз с помощью оптической схемы интерференционного опыта Юнга и визуальных наблюдений смещения интерференционных полос при смене реализаций спекл-поля [15]. Однако большая трудоёмкость такого метода позволила провести исследования только для одной кольцевой апертуры источника и при сравнительно малом числе реализаций спекл-поля. С помощью цифровых средств обработки изображений в натурном и численном экспериментах возможно использование случайной выборки с достаточно большим числом значений, что намного повышает статистическую достоверность получаемых результатов. Поэтому цель данной работы состояла в установлении с помощью численного и натурного экспериментов закономерностей статистического распределения разности фаз в спекл-полях, формируемых источниками с апертурами различной формы, и в установлении связи этих закономерностей с пространственными корреляционными свойствами развитых спекл-полей.

Функция поперечной корреляции комплексной амплитуды спекл-модулированного поля в дальней области дифракции

Возможная причина возникновения неравномерности статистического распределения разности фаз в дифракционном спекл-модулированном поле, как мы полагаем, может быть связана с пространственными корреляционными свойствами спекл-поля. Возможные знакопеременные осцилляции поперечной корреляционной функции спекл-поля статистически предопределяют в соответствующих точках поля разность фаз поля в π радиан. Сильные осцилляции корреляции в рассеянном поле в дальней области дифракции формируются при использовании симметричных и периодических апертур источников.

Пространственная корреляционная функция комплексной амплитуды спекл-поля в дальней области дифракции определяется на основании теоремы Ван

Циттерта–Цернике как Фурье-образ распределения средней интенсивности по источнику диффузнорассеянного когерентного излучения [1, 2, 21]. Следовательно, для источников с равномерным распределением средней интенсивности и апертурой, форма которой имеет симметрию вращения чётного порядка, корреляционная функция поля принимает действительные знакопеременные значения.

В нашей работе были рассмотрены апертуры источника спекл-поля разной формы: треугольник, круг, сплошной квадрат, кольцо, кольцевой квадрат и два прямоугольника (рис. 1). Распределения нормированной средней интенсивности I ( x , у ) по апертурам таких источников можно записать соответственно выражениями

, .   [ 1, 0 <  у <  ( - V3| x | + 3aa /2);

• 11    (x, У ) = 1

[ 0, в остальных случаях;

• 1 ₂    ( r ) = circ ( r / a ) , где r = x ² + у ² ;

• 1 ₃    ( x, у ) = rect ( x / a ) x rect ( у / a ) ;

• 1 4    ( r ) = circ ( r / a ) - circ ( r / b ) ;                        ⁽¹⁾

• 1 5    ( x , у ) = rect ( x / a ) x rect ( у / a ) -

  - rect ( x / b ) x rect ( у / b ) ;

• 1 6    ( x , у ) = rect ( x / a ) x rect ( у / a ) -

  - rect ( x / b ) x rect ( у / a ) .

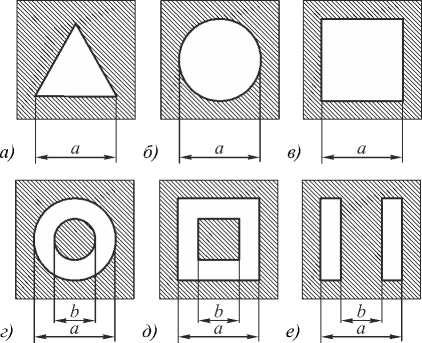
Рис. 1. Апертуры рассеивателей – источников спекл-полей: а) треугольник; б) круг; в) квадрат; г) кольцо; д) кольцевой квадрат; е) два прямоугольника

Для автокорреляционных функций комплексной амплитуды спекл-полей в дальней области дифракции для источников, имеющих апертуры в форме круга, сплошного квадрата, кольца, кольцевого квадрата и двух прямоугольников, можно получить выражения [22], представленные ниже, в которых Ap = ^/ A^ ² + An ² , B { I ( r ) } - преобразование Фурье-

Бесселя, J 1 (2 n a Ap ) - функция Бесселя первого рода первого порядка, F { I ( x , у ) } - преобразование Фурье.

G ₂(Ap) = B{ 1 2( r )} =

aJ 1 (2na Ap) ^AP

G ₃(A£, An) = F{ 1 ₃( x , у )} = a ²sinc ( a A^) sinc ( a An);

G ₄(Ap) = B{ 1 ₄( r )} =

aJ 1 (2n a Ap) bJ 1 (2n b Ap) ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^a  ^^^^^s  ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^a

Ap        Ap

G ₅(A^, An) = F{ 1 ₅( x , у )} =

= a ²sinc ( a A^ sinc( a An)- b ²sinc ( b A^) sinc ( b An);

G ₆(A^, An) = F{ 1 ₆( x , у )} =

= a ²sinc ( a A^ sinc ( a An) - ab sinc ( b A^) sinc ( a An) .

На рис. 2 представлены двухмерные графики нор-

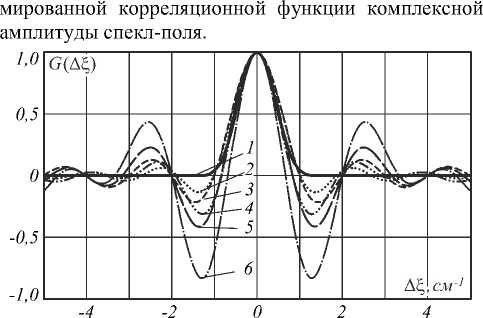
Рис. 2. Нормированные корреляционные функции комплексной амплитуды спекл-поля при Ar] = 0 для источников с апертурами в форме: треугольника (1); круга (2); квадрата (3); кольца (4); квадратного кольца (5);

двух вертикальных прямоугольников (6);

a/b=2; a=10 мм (рис. 1)

Изменение знака корреляционной функции спекл-поля позволяет сделать предположение о наиболее вероятном изменении знака комплексной амплитуды поля при переходе от спекла к спеклу. Это означает, что с наибольшей вероятностью колебания поля в соседних спеклах происходят в противофазе и, таким образом, имеет место неравномерность плотности распределения разности фаз в соседних спеклах с наиболее вероятным значением π радиан.

Численный статистический эксперимент

Для исследования неравномерности пространственного фазового распределения в спекл-поле в дальней области дифракции выполнен численный статистический эксперимент по определению разности фаз в различных точках спекл-поля. Моделирование источника спекл-поля производилось согласно следующему алгоритму. Генерировались две матрицы случайных независимых вещественных величин g_k и g_j , распределённых от –1 до 1 по нормальному закону. На их основе формировалась матрица случайных комплексных переменных g k + ig j . Таким образом создавалось случайное δ-коррелированное поле круговых Гауссовых комплексных величин [23]. Данное поле модулировалось бинарной апертурной функцией

P ( k , j ) , равной 1 в пределах апертуры и 0 за её пределами. Распределение комплексной амплитуды поля в плоскости источника задавалось в виде дискретного массива независимых круговых Гауссовых случайных величин U ( k , j ) = ( g_k + ig_j ) P ( k , j ) .

Фурье-преобразование этого поля формировало спекл-поле в дальней области дифракции. Проводилась случайная выборка двух точек K ₁ и K ₂ в смоделированном спекл-поле, и определялась разность фаз поля в этих точках. Точки располагались на определённом расстоянии ∆ξ друг от друга по отношению к размерам спеклов. На рис. 3 приведена схема натурного эксперимента, соответствующего вышеописанной числовой процедуре.

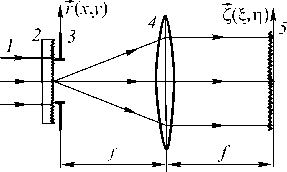
Рис. 4. Фрагменты смоделированных спеклограмм, формируемых рассеивающими источниками с апертурными диафрагмами в форме: а) треугольника; б) квадрата; в) квадратного кольца;

г) двух прямоугольников

б)

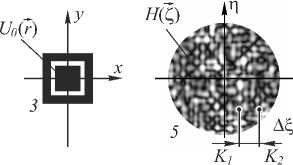
Рис. 3. Схема натурного эксперимента для определения разности фаз в точках спекл-поля в дальней области дифракции: 1 – лазерный пучок, 2 – рассеиватель, 3 – апертура, 4 – линза, 5 – спекл-поле в дальней области дифракции

В численном эксперименте возможно определение разности фаз в полном интервале [0,2 π ], включая границы интервала. Однако в натурном эксперименте, результаты которого представлены ниже, невозможно отличить разность фаз в (0 ± δφ ) и (2 π ± δφ ) рад, где δφ - погрешность определения разности фаз. Поэтому для корректного сопоставления результатов численного и натурного экспериментов мы вынуждены были ограничиться и в численном эксперименте определением разности фаз в интервале [0, π ].

С помощью численного моделирования формировались спекл-поля, создаваемые с использованием апертур в форме треугольника, квадрата, кольцевого квадрата и двух вертикальных прямоугольников, соотношение размеров a/b =2 (рис. 1). Фрагменты спекл-картин, соответствующие этим апертурам, представлены на рис. 4. В численном эксперименте на основании выборки из 3600 значений строились гистограммы статистического распределения разности фаз в двух точках для различных расстояний ∆ξ (рис. 5–7). Выбирались характерные по отношению к среднему размеру спеклов ε _⊥ расстояния ∆ξ между точками смоделированного спекл-поля.

Средний размер спеклов ε _⊥ определялся как среднее расстояние между двумя соседними минимумами интенсивности спекл-поля. Такой подход вполне применим также для случая апертуры в форме двух прямоугольников, когда дифракционное спекл-поле формируется в результате интерференции спекл-полей, образованных отдельными частями такой апертуры. Несмотря на то, что в этом случае в горизонтальном направлении интерференционная картина имеет квазирегулярный характер (рис. 4 г ), логично и целесообразно определять размер спекла так же, как среднее расстояние между минимумами интерференционной картины.

Как видно из гистограмм (рис. 5–7), наиболее вероятные значения для разности фаз находятся вблизи 0 и π радиан. Если исходить из представления о равновероятном значении разности фаз в спеклах, то приведённые данные не поддаются объяснению. Напротив, представление, что наиболее вероятной является разность фаз в соседних спеклах π радиан, позволяет объяснить наблюдаемую картину.

При расстоянии ∆ξ между точками спекл-поля, равном половине размера спекла, наиболее вероятно их попадание в один спекл, но не исключается возможность попадания и в соседние спеклы. В этом случае наиболее вероятны значения разности фаз вблизи 0. При расстоянии ∆ξ , равном среднему раз- меру спекла, равновероятно попадание точек и в один, и в соседние спеклы. При расстоянии ∆ξ , равном значению 1,5 среднего размера спекла, наиболее вероятно, что точки при случайной выборке попадают в соседние спеклы, но не исключается возможность их попадания и в один спекл. При расстоянии ∆ξ , равном значению 2,5 среднего размера спекла, наиболее вероятно, что точки при случайной выборке попадают в спеклы через один, но не исключается возможность попадания в соседние спеклы и даже в

один спекл. В этом случае наиболее вероятны значения разности фаз вблизи 0, что и наблюдается на соответствующих гистограммах.

N " 800 -

ТУГ 800-

400-

о

ПППппгДф

400-

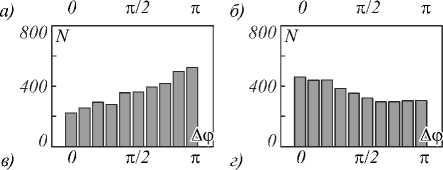
Рис. 5. Гистограммы распределения разности фаз в двух точках смоделированного спекл-поля, создаваемого рассеивающим источником с апертурной диафрагмой в форме квадрата. Отношение расстояния между точками спекл-поля ∆ξк среднему размеру спеклов ε⊥ равно: a) 0,5; б) 1; в) 1,5; г) 2,5

Следует отметить, что наблюдаемое статистическое распределение разности фаз (пунктирные линии на рис. 8) отличается от теоретически предсказываемого в виде суммы двух δ -функций (сплошные линии на рис. 8). Данное обстоятельство может быть, в частности, объяснено следующими соображениями. Строго говоря, условие δ -коррелированности диффузно-рассеивающе-го источника из-за конечности поперечных размеров рассеивающих неоднородностей на его поверхности практически невыполнимо [23]. Это приводит к нарушению симметрии в распределении средней интенсивности в симметричной апертуре рассеивателя и, как следствие, к уширению локальных максимумов плотности распределения вероятности разности фаз (рис. 8). В численном моделировании асимметрия обусловлена различием амплитуд поля в симметрично расположенных пикселях. Таким образом, можно только предполагать наиболее вероятное значение разности фаз в π рад

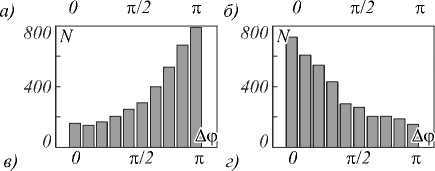
Рис. 6. Гистограммы распределения разности фаз в двух точках смоделированного спекл-модулированного поля, создаваемого рассеивающим источником с апертурной диафрагмой в форме кольцевого квадрата. Отношение расстояния ∆ξк среднему размеру спеклов ε _⊥ равно: a) 0,5; б) 1; в) 1,5; г) 2,5

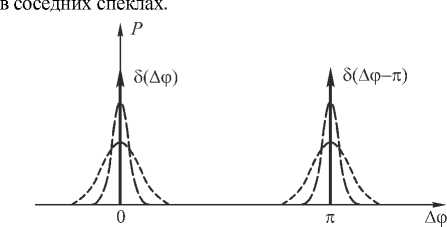
Рис. 8. Уширение функции распределения разности для реального рассеивающего объекта с конечными поперечными размерами неоднородностей

Чтобы подчеркнуть частный характер отмеченной особенности спекл-полей, аналогичное моделирование было проведено для полей, создаваемых рассеивающими источниками, апертура которых не обладает вращательной симметрией чётного порядка. На рис. 9 представлены гистограммы для рассеивающего объекта в форме треугольника.

1200 -№

N ~

1200-

a)

800-

400-

0"_ в)

О к!2 л

г)       О к!2 л

Рис. 7. Гистограммы распределения разности фаз в двух точках смоделированного спекл-модулированного поля, создаваемого рассеивающим источником с апертурной диафрагмой в форме двух вертикальных прямоугольников. Отношение расстояния∆ξк среднему размеру спеклов ε _⊥ равно: a) 0,5; б) 1; в) 1,5; г) 2,5

Ппг-1г4ф|

О

О

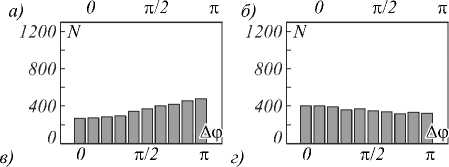
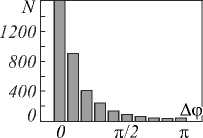
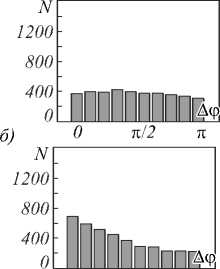
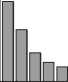
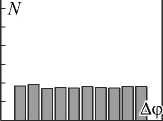
Рис. 9. Гистограммы распределения разности фаз в двух точках смоделированного спекл-поля, создаваемого рассеивающим источником с апертурной диафрагмой

в форме треугольника. Отношение ∆ξ к ε _⊥ равно:

a) 0,5; б) 1; в) 1,5; г) 2,5

Наблюдается выраженный максимум распределения разности фаз вблизи 0 для точек, попадающих в один спекл (рис. 9 а ). Во всех остальных случаях на-

блюдается практически равномерное распределение по всему интервалу (0, п ), рис. 9 б-г . В этом случае разность фаз в соседних спеклах приблизительно равномерно распределена в интервале (0, п ).

Гистограммы на рис. 5–8 показывают, что изменение знака корреляционной функции комплексной амплитуды спекл-поля (рис. 2) связано с изменением знака комплексной амплитуды поля при переходе от спекла к спеклу. Чем больше по модулю величина первого отрицательного максимума автокорреляционной функции, тем больше неравномерность распределения разности фаз.

Влияние формы апертуры на статистическое распределение разности фаз в двух точках спекл-поля в дальней области дифракции

Согласно вышесказанному можно предположить, что чем больше по модулю значения экстремумов автокорреляционной функции комплексной амплитуды спекл-поля, тем больший максимум плотности распределения разности фаз в двух точках спекл-поля будет наблюдаться. Проследим эту закономерность

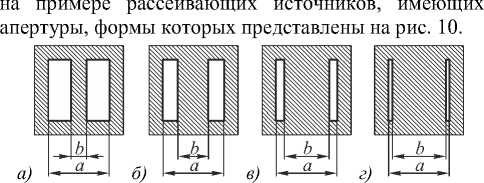
Рис. 10. Апертуры рассеивателей – источников спекл- полей, в форме двух параллельных прямоугольников: а) a/b=4; б) a/b=2; в) a/b=4/3; г) a/b=8/7

Распределения нормированной средней интенсивности I ( x , y ) по апертурам таких источников можно записать, соответственно, в следующем виде: I 1 ( x , y ) = rect ( x ) x rect ( y ) ;

• 1 2    ( x , y ) = rect ( x ) x rect ( y ) - rect ( 4 x ) x rect ( y ) ;

• 1 3    ( x , y ) = rect ( x ) x rect ( y ) - rect ( 2 x ) x rect ( y ) ;      (3)

• 1 ₄    ( x , y ) = rect ( x ) x rect ( y ) - rect ( 4 x /3 ) x rect ( y ) ;

• 1 5    ( x , y ) = rect ( x ) x rect ( y ) - rect ( 8 x П ) x rect ( y ) .

Поперечную корреляционную функцию комплексной амплитуды спекл-поля в дальней области дифракции определим как Фурье-образ распределения средней интенсивности по апертуре источника диффузно-рассеянного когерентного излучения [22]: G 1 ( A^ , An ) = F { 1 1 ( x , y ) } = sinc ( A^ ) sinc ( An ) ;

G 2 ( A^ , An ) = F { 1 2 ( x , y ) } =

= sinc ( A^ ) sinc ( An ) - ( 1/4 ) sinc ( A^ /4 ) sinc ( An ) ;

G 3 ( A^ , An ) = F { I з ( x , y ) } =

= sinc ( A^ ) sinc ( An ) - ( 1 /2 ) sinc ( A^ /2 ) sinc ( An ) ;

G 4 ( A^ , An ) = F { 1 4 ( x , y ) } =

= sinc ( A^ ) sinc ( An ) - ( 3/4 ) sinc ( 3 A^ /4 ) sinc ( An ) ;

G ₅( A^ , An ) = F { 1 ₅( x , y ) } =

= sinc ( A^ ) sinc ( An ) - ( 7/8 ) sinc ( ? A^ / 8 ) sinc ( An ) .

На рис. 11–12 представлены графики нормированных корреляционных функций комплексной амплитуды спекл-поля для источников с апертурами в форме квадрата и двух вертикальных прямоугольников. Графики функций получены при различных отношениях a/b (рис. 10) . Для рис. 11 остаётся постоянным размер a= 10 мм, для рис. 12 - расстояние между центрами прямоугольников, ( a + b ) / 2 = 10 мм.

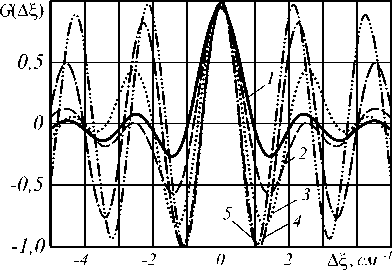
Рис. 11. Нормированные корреляционные функции комплексной амплитуды спекл-поля для источников с апертурами в форме: 1) квадрата (рис. 1а); 2-5) двух вертикальных прямоугольников (рис. 10); a=10 мм;

отношение a/b равно: 2) 4; 3) 2; 4) 4/3; 5) 8/7

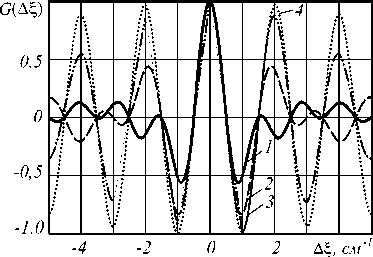
Рис. 12. Нормированные корреляционные функции комплексной амплитуды спекл-поля для источников с апертурами в форме двух вертикальных прямоугольников, отношения a/b: 1) 4; 2) 2; 3) 4/3; 4) 8/7; расстояние между центрами прямоугольников ( a + b )/ 2 =10 мм

На рис. 11, 12 видно, что при уменьшении отношения a/b, вызванном уменьшением ширины прямоугольников, увеличиваются по модулю значения локальных максимумов корреляционной функции поля. Фото спекл-картин на рис. 13 показывают, как изменяется форма и размер спеклов при уменьшении ширины прямоугольников.

Важно проследить изменение величины максимума плотности распределения вероятности разности фаз в двух точках спекл-поля в зависимости от изменения параметров апертуры источника и, соответственно, от изменения величины локальных максимумов корреляционной функции комплексной амплитуды поля. На рис. 14 представлены гистограммы статистического распределения разности фаз в двух точках спекл-поля, создаваемого источником с апертурой в форме двух вертикальных прямоугольников, при расстоянии Д^ между точ- ками, равном 1,5 среднего размера спеклов. В этом случае наиболее вероятно, что точки при случ айной выборке попадают в соседние спеклы и наиболее вероятные значения для разности фаз находятся вблизи прадиан.

a)

Рис. 13. Фрагменты смоделированных спеклограмм, формируемых рассеивающими источниками с апертурами в форме двух прямоугольников; расстояние между центрами прямоугольников ( a + b ) / 2 = 10 мм,

б)

соотношение a/b равно: а) 4; б) 2; в) 4/3; г) 8/7

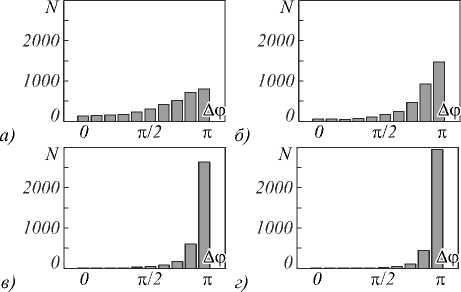
Рис. 14. Гистограммы распределения разности фаз в двух точках смоделированного спекл-поля для рассеивающего источника с апертурой в форме двух параллельных прямоугольников; А§ равно 1,5 среднего размера спеклов, a/b равно: 1) 4; 2) 2; 3) 4/3; 4) 8/7

На рис. 11, 12, 14 видно, что при увеличении по модулю значений локальных максимумов корреляционной функции комплексной амплитуды спекл-поля увеличиваются максимальные значения гистограмм. Проследим эту закономерность на примере рассеивающего источника с апертурой в форме кольца.

Распределения нормированной средней интенсивности по рассеивающим источникам, имеющим форму кольца, с различной шириной кольцевой области (рис. 15), можно записать выражениями:

• 1 1    ( r ) = circ ( r ) ;

• 1 2    ( r ) = circ ( r ) - circ ( 4 r ) ;

• 1 3    ( r ) = circ ( r ) - circ ( 2 r ) ;                            (5)

• 1 ₄    ( r ) = circ ( r ) - circ ( 4 r /3 ) ;

• 1 ₅    ( r ) = circ ( r ) - circ ( 8 r / 7 ) .

Для таких центрально-симметричных объектов Фурье-образ можно записать в полярной системе координат как функцию одной координаты [21]. Корреляционную функцию комплексной амплитуды спекл-поля в дальней области дифракции определим c помощью преобразования Фурье–Бесселя [22]:

G ( Др ) = B { I ( r ) } = J ^{1 (2 пДр )} ;

Др

• _С 2 ( ДР ) = B { 1 2 ( r ) } = M - J ^Z ;

Др       4Др

G ( Др ) = B { I, ( r ) }= J ^) -.^р^а );   (6)

Др       2Др

W = B { 1 4 ( r ) } = J i ^l n^e ) - “ ;^Vl ;

Др       4ДрG (Др) = B{ I, (r )}=« - 2»^).Др        8Др

• а)               б)               в)               г)

Рис. 15. Апертуры рассеивателей – источников спекл-полей в форме кольца с внешним диаметром a=10 мм:

• а) a/b=4; б) a/b=2; в) a/b=4/3; г) a/b= 8/7

На рис. 16 представлены нормированные корреляционные функции комплексной амплитуды спекл-поля при различных соотношениях внешнего и внутреннего диаметров кольца a/b, при a= 10 мм (рис. 15) . Каким образом изменяется форма и размер спеклов при изменении толщины кольца, показано на рис. 17.

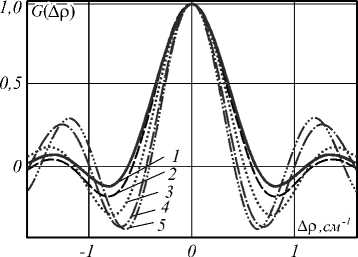
Рис. 16. Нормированные корреляционные функции комплексной амплитуды спекл-поля для рассеивающих источников с апертурами, имеющими формы: 1) круга с диаметром a=10 мм (рис. 1а); 2-5) кольца, внешний диаметр a=10 мм, соотношение внешнего и внутреннего диаметров кольца a/b (рис. 15) равно:

2) 4; 3) 2; 4) 4/3; 5) 8/7

a)

б)

Рис. 17. Фрагменты смоделированных спеклограмм, формируемых рассеивающими источниками с апертурами в форме кольца; соотношение внешнего и внутреннего диаметров кольца a/b равно:

а) 4; б) 2; в) 4/3; г) 8/7

На рис. 18 представлены гистограммы статистического распределения разности фаз в двух точках при расстоянии ∆ξ между ними, равном 1,5 среднего размера спеклов, когда предполагается наиболее вероятным попадание этих точек в соседние спеклы.

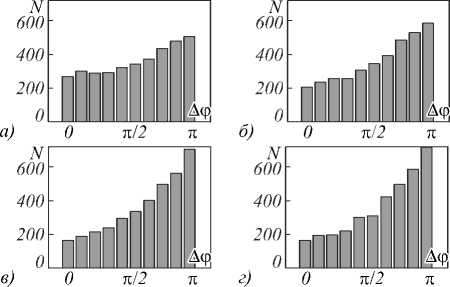
Рис. 18. Гистограммы распределения разности фаз в двух точках смоделированного спекл-поля для рассеивающего источника с апертурой в форме кольца (рис. 15) с внешним диаметром a=10 мм; ∆ξравно 1,5 среднего размера спеклов; отношение внешнего диаметра кольца к внутреннему a/b равно: а) 4; б) 2; в) 4/3; г) 8/7

Из рис. 16 и 18 видно, что в этом случае также прослеживается связь между увеличением значения модуля первого локального максимума корреляционной функции комплексной амплитуды спекл-поля и увеличением максимума плотности распределения вероятности разности фаз в π радиан в двух точках спекл-поля при их наиболее вероятном попадании в соседние спеклы. Этот эффект менее выражен, чем в случае апертуры источника в форме двух прямоугольников, поскольку меньше по модулю значение первого локального максимума корреляционной функции. Тем не менее отчетливо наблюдается эффект увеличения максимума плотности распределе- ния вероятности разности фаз при увеличении значения модуля первого локального максимума корреляционной функции комплексной амплитуды поля.

Натурный статистический эксперимент по определению разности фаз в двух точках спекл-поля с использованием интерферометра Юнга

В работе [15] нами уже был выполнен натурный статистический эксперимент по определению разности фаз в двух точках спекл-поля с использованием интерферометра Юнга, но со сравнительно малым значением выборки N = 150 . Гистограммы статистического распределения разности фаз определялись при использовании рассеивающего источника с апертурой только одной формы и при трёх расстояниях между точечными отверстиями в интерферометре Юнга. Смещение интерференционных полос в интерферометре при смене реализаций спекл-поля определялось визуально с помощью микроскопа.

В связи с развитием технических средств регистрации и обработки стало практически возможным проведение натурного эксперимента с реализацией выборки с достаточно большим числом значений для рассеивающих источников с апертурой разных форм. В настоящей работе реализован статистический эксперимент с числом выборки N = 1000 для каждой гистограммы; использованы апертуры, ограничивающие рассеивающий источник, четырёх форм: квадрат, кольцевой квадрат, треугольник, кольцевой треугольник – при двух различных расстояниях между точечными отверстиями в интерферометре Юнга. В ходе эксперимента было сформировано восемь выборок, по которым построено восемь гистограмм.

На рис. 19 представлена схема реализации натурного эксперимента по определению разности фаз в двух точках спекл-поля с использованием схемы интерферометра Юнга.

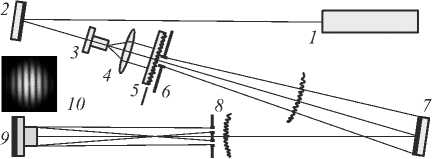
Рис. 19. Схема натурного эксперимента по определению разности фаз в двух точках спекл-поля с использованием схемы интерферометра Юнга: 1 – лазер, 2, 7 – зеркала, 3 – микрообъектив, 4 – линза, 5 – рассеиватель, 6 – апертура, 8 – экран с двумя точечными отверстиями, 9 – цифровая камера, 10 – изображение интерференционных полос на матрице цифровой камеры

Пучок света от лазера 1 отражается от зеркала 2, расширяется с помощью микрообъектива 3, коллимируется линзой 4 и проходит через рассеиватель 5, ограниченный апертурой 6. Расстояние z от апертуры 6 до экрана с двумя отверстиями 8 много больше размера апертуры. Внешний размер апертуры D ≈ 5 мм , расстояние z ≈ 1500 мм , поэтому можно считать, что плоскость экрана с отверстиями 8, на которую попадает спекл-поле, находится в дальней области дифракции. Зарегистрированные спекл-картины, формирующиеся в плоскости экрана 8, представлены на рис. 20.

а                       б

Рис. 20. Формы апертур рассеивающих источников (а) и фрагменты создаваемых этими источниками спекл-картин (б), зарегистрированных в дальней области дифракции.

Физические размеры кадров с апертурами ≈7×7 мм, со спекл-картинами ≈2×4,5 мм

В эксперименте использовались лазер непрерывного линейно поляризованного излучения ГН-50 (мощность – 25 мВт, длина волны – 0,63 мкм) и цифровая фотокамера DCM 510 (размер КМОП-матрицы – 5,7 × 4,28 мм, в пикселях – 2592 × 1944). На рис. 21 представлена фотография экспериментальной установки.

Рис. 21. Общий вид экспериментальной установки для реализации натурного статистического эксперимента по определению разности фаз в двух точках спекл-поля с использованием схемы интерферометра Юнга

В эксперименте расстояние между отверстиями на экране 8, рис. 19, равное ∆ξ = 0,5 мм , не менялось, а отношение ∆ξ к среднему размеру спеклов ε⊥ , равное 1,5 и 2,5, ∆ξ ≈ 1, 5ε⊥ , ∆ξ ≈ 2, 5ε⊥ , обеспечивалось путём изменения расстояния z0 от апертуры 6 до экрана 8. Средний поперечный размер спеклов определялся путём численной обработки изображения спекл-картины как среднее расстояние между двумя соседними минимумами в пространственном распределении интенсивности. Расстояние z0 принимало два значения z01 = 250 см и z02 = 150 см , при которых средние поперечные размеры спеклов равны ε⊥ ≈ 0,3 мм и ε⊥ ≈ 0,2 мм . Выборки формировались при двух расстояниях z0 до экрана 8, в которых ∆ξ / ε⊥ равнялось 1,5 и 2,5.

На матрице цифровой фотокамеры 9 регистрировалось дифракционное гало с системой интерференционных полос 10 (рис. 19). Величина периода полос Λ зависит от расстояния ∆ξ между отверстиями и расстояния z между экраном 8 и матрицей цифровой фотокамеры 9, Λ = λz/∆ξ . Положение полос зависит от разности фаз в спеклах, которые попадают на отверстия в экране. При поперечном смещении рассеивателя 5 на величину, равную размеру апертуры, происходит полная смена реализации спекл-поля на поверхности экрана с отверстиями 8. Положение полос на матрице меняется, если изменяется разность фаз ∆φ колебаний поля в отверстиях. Изменение разности фаз ∆φ поля в отверстиях экрана можно определить по величине сдвига интерференционных полос ∆ x ' в долях их периода Λ :

∆φ = 2 π∆ x '/ Λ . (7)

Изображение дифракционного гало с системой интерференционных полос, зарегистрированное на матрице цифровой фотокамеры, представлено на рис. 22.

Рис. 22. Смещение интерференционных полос в дифракционном гало при смене реализации спекл-поля.

Период интерференционных полос на матрице фотокамеры ≈ 0,45 мм (200 пикс.)

Снимались N = 1000 подобных изображений при разных реализациях спекл-поля на экране с точечными отверстиями для каждой апертуры источника и для каждого расстояния ∆ξ ≈ 1, 5ε⊥ и ∆ξ ≈ 2, 5ε⊥ . За- регистрированные изображения обрабатывались, определялся сдвиг интерференционных полос Ах' в каждом изображении относительно некоторого опорного изображения (рис. 22), и определялось изменение разности фаз Аф по формуле (7).

Смещение интерференционных полос А х ' определялось корреляционным методом как абсолютная величина смещения центрального пика функций взаимной корреляции распределений интенсивностей 1 ₀( х ', у ') и I_t ( х ', у ') опорного и текущего изображе-

ний интерференционных полос относительно положения центрального пика функции автокорреляции

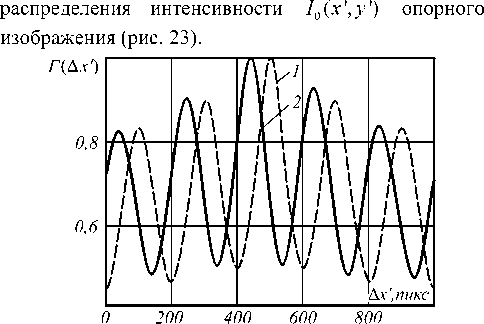
Рис. 23. Нормированные функции: 1) автокорреляции

распределения интенсивности 1 ₀ ( х ', у ') в опорном изображении интерференционных полос; 2) взаимной корреляции распределений интенсивностей 1 ₀ ( х ', у ')

и I_t ( х ', у ') в опорном и текущем изображениях интерференционных полос

Функции автокорреляции распределения интенсивности 1 ₀( х ', у ') и взаимной корреляции распределений интенсивностей 1 ₀( х ', у ') и I i ( х ', у ') можно записать следующими выражениями, в которых ( х ', у ') - дискретные координаты пикселей матрицы с записями интенсивностей; n х m - размер матрицы в пикселях.

nm

^Г 0^{( А х} ', ^А у ) = У У I 0^{( х} ', у ') I 0^{( х} ' ^{-А х} ', у ' ^-А у ');

х ' = 1 у ' = 1

nm

Г i ( А х ', А у ') = У У 1 0 ( х ', у ') I n ( х ' -А х ', у ' - А у ').

х ' = 1 у ' = 1

При значениях ( А х ', А у '), равных величине сдвига интерференционных полос, функция Г i ( А х ', А у ') принимает максимальное значение, наблюдается пик корреляции. Поскольку в эксперименте смещение интерференционных полос происходит только вдоль оси X, можно анализировать функции корреляции одной переменной Г i ( А х ')(рис. 23).

Программа обработки поочерёдно считывает текущие изображения, сравнивает (корреляционно) с опорным изображением, определяет абсолютное значение сдвига центрального пика функции взаимной

корреляции Г i ( А х ', А у ') распределений интенсивно-

сти относительно положения центрального пика функции автокорреляции Г ₀( А х ', А у '). Согласно (7)

определяется Аф для каждого текущего изображения и заносится в соответствующую ячейку вектора-строки. На основе полученных данных построены гистограммы, представленные на рис. 24.

400-

400-

200 ■

О _

a)

N~

400-

пппПпППпП 4Ф

О к(2 к

200- оШпППпППпоЬр

200 ■

О _

б)

N

400-

пППППгПг—.ГпГФф

ппПп.тПЫ

0 _

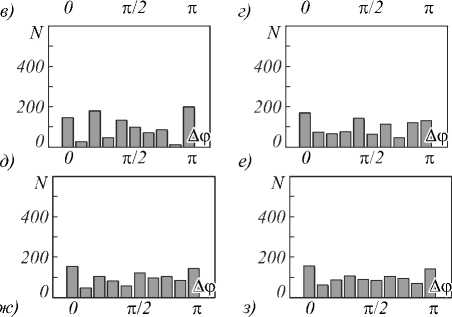
Рис. 24. Гистограммы распределения плотности вероятности разности фаз ∆φ в двух точках спекл-поля, создаваемого источником с апертурой в форме: (а, б) кольцевого квадрата; (в, г) квадрата; (д, е) кольцевого треугольника; (ж, з) треугольника. Расстояния ∆ξ между

отверстиями в интерферометре Юнга равно: (а,в,д,ж) - ∆ξ ≈ 1,5 ε _⊥ ; (б,г,е,з) - ∆ξ ≈ 2,5 ε _⊥

Приведённые на рис. 24 а-г гистограммы показывают отчётливую неравномерность плотности распределения вероятности разности фаз в двух точках спекл-поля для источников, имеющих апертуру в форме кольцевого квадрата и просто квадрата. Для таких источников, как было сказано выше, корреляционная функция дифракционного поля имеет достаточно выраженные локальные максимумы. Чем больше по модулю значения локальных максимумов, тем больше локальные максимумы плотности распределения вероятности разности фаз, что и наблюдается на рис. 24 в случае кольцевого квадрата. При А^ =1,5 е_± , когда отверстия в интерферометре Юнга с наибольшей вероятностью попадают в соседние спеклы, максимум плотности распределения вероятности разности фаз наблюдается при значении Аф = п рад. При А^ = 2,5 е_± , когда отверстия в интерферометре Юнга с наибольшей вероятностью попадают в спеклы через один, максимум наблюдается при Аф =0.

Следует отметить характерную особенность гистограмм, полученных в натурном эксперименте. На рис. 24 а-г наблюдается не плавное увеличение максимума, как в численном эксперименте, а скачком вблизи 0 и π рад, и почти равномерное распределение значений разности фаз на всём остальном промежутке. Это можно объяснить тем, что при проведении натурного статистического эксперимента, при смене реализаций спекл-поля, отбирались только яркие и чёткие изображения дифракционного гало с системой интерференционных полос. В этих случаях оба отверстия интерферометра Юнга попадают в светлые области, в нашем эксперименте или в соседние спеклы, или через один, и наиболее вероятно, что значения разности фаз равны или π рад, или 0. Если изображение не было ярким и чётким, смещали дальше рассеиватель до получения «хорошей» картины. При случайной выборке в численном эксперименте учитывались все попадания точек: и в центральные области спеклов, и в их окрестности, и на границы, – что приводило к плавному увеличению максимума плотности распределения вероятности разности фаз.

Величина максимума плотности распределения вероятности разности фаз на рис. 24 б, г больше для расстояния ∆ξ ≈ 2, 5 ε _⊥ , когда отверстия в интерферометре Юнга с наибольшей вероятностью попадают в спеклы через один, чем на рис. 24 а, в для расстояния ∆ξ ≈ 1, 5 ε _⊥ , когда отверстия в интерферометре Юнга с наибольшей вероятностью попадают в соседние спеклы. Это можно объяснить техническими особенностями эксперимента. Для реализации условий равенства Д^ = 1,5 г_± и А^ = 2,5 г_± изменяли расстояние z 0 от апертуры 6 до экрана с двумя отверстиями 8 (рис. 19); расстояние z 0 принимало два значения z ₀₁ = 250 см и z ₀₂ = 150 см . При увеличении расстояния z ₀ средняя интенсивность поля уменьшается. Изображения интерференционных полос в дифракционном гало становятся менее яркими, так как регистрируется меньше «хороших» картин.

Корреляционная функция поля, создаваемого рассеивающим источником с апертурой в форме треугольника или кольцевого треугольника (рис. 20), не имеет локальных максимумов, поэтому предполагается равномерная плотность распределения вероятности разности фаз. Результаты натурных экспериментов подтверждают данное предположение для источников с несимметричными апертурами, рис. 24 д-з .

Заключение

С помощью средств компьютерного моделирования возможна реализация случайной выборки с числом значений на порядки больше, чем в натурном эксперименте. Поэтому результаты численного статистического эксперимента могут служить весомым аргументом в подтверждении статистического свойства неравномерности распределения разности фаз в спекл-поле в дальней области дифракции для некоторого класса форм апертур источников спекл-полей.

Результаты численного моделирования и экспериментальных исследований подтверждают теоретические положения о том, что в развитом спекл-поле разность фаз в двух точках принимает наиболее вероятные значения 0 и π радиан для апертур источников симметричной формы. На гистограммах, полученных в ходе проведения и натурного эксперимента, и моделирования, заметна отчётливая неравномерность плотности распределения вероятности разности фаз в развитом дифракционном спекл-поле. Необходимым условием увеличения значения максимумов статистического распределения разности фаз является увеличение по модулю значений локальных максимумов автокорреляционной функции комплексной амплитуды поля. Это обеспечивается использованием источников спекл-поля с апертурой определённой формы.

Неравномерность распределения разности фаз в двух точках спекл-поля, создаваемого источниками с апертурой определённого класса, может позволить в ряде случаев восстановить утраченную при записи спеклограмм фазовую информацию об объектном поле, что может быть положено в основу методов восстановления фазы спекл-поля по его интенсивности – спеклограмме, и восстановления информации о рассеивающем источнике. Знание статистических свойств разности фаз в спекл-поле также имеет практическое значение для оценки статистических параметров сигнала лазерных спекл-интерферометров микроперемещений объектов с рассеивающими поверхностями [24].

Авторы благодарят Д.В. Лякина и О.А. Перепелицыну за помощь в экспериментальных исследованиях.