Особенности структуры семейства траекторий на плоскости и фокусировка пучков заряженных частиц

Для научного творчества Ю.К. Голикова характерно широкое использование современного математического аппарата при анализе ионнооптических систем. Одним из таких современных и эффективных методов является интенсивно развиваемый в последние десятилетия аппарат теории особенностей отображений дифференцируемых многообразий, более известной как "теория катастроф" [1]. Этот аппарат позволяет с единых позиций, абстрагируясь от частностей, анализировать общие свойства семейства траекторий.

Как в волновой, так и в корпускулярной оптике понятие фокусировки тесно связано с понятием каустики. Каустики, их форма и особенности, являются важнейшими характеристиками семейства траекторий. Они определяются из условия обращения в нуль гессиана классического действия на траектории

H ( $ ) = d 2 sd 2 s (.^ Y = 0. (1) da l da 2 ( da_xda ₂ )

Здесь S ( r , a ₁ , a ₂) — полный интеграл стационарного уравнения Гамильтона—Якоби, которое для задачи о движении частицы массы m и с зарядом q в электростатическом поле с потенциалом U ( r ) имеет вид

( V S ) 2 = 2 m ( E - qU ( r ) ) = P² ( r ) . (2)

Параметры a1 и a2 в уравнении (1) задают совокупность траекторий, выходящих из заданной поверхности, координатами на которой можно считать эти параметры. Для центрального поля траекторий a1 и a2 определяют направление выхода траекторий из заданной точки.

Каустики являются огибающими данного семейства траекторий. На каустиках обращается в бесконечность кривизна волнового фронта S ( r , a ₁ , a ₂) = const. Вблизи каустики резко возрастает концентрация траекторий. При пересечении каустики изменяется число траекторий, приходящих в заданную точку [1]. Каустики играют важную роль в задачах о нахождении коротковолновых асимптотик уравнений Гельмгольца и Шредингера [2–4].

АНАЛИЗ ПРЯМОЛИНЕЙНЫХ ТРАЕКТОРИЙ НА ПЛОСКОСТИ

Рассмотрим семейство прямолинейных траекторий на плоскости. Такими семействами описывается широкий класс электронно-оптических систем на основе двумерных электростатических полей [5]. Эти же семейства характеризуют оптические свойства систем на основе электростатических полей, обладающих осевой симметрией, в тех случаях, когда достаточно ограничиться траекториями в меридиональной плоскости, когда, например, точечный источник заряженных частиц находится на оси системы. Кроме того, поскольку в большинстве случаев плоскость фокусировки (плоскость изображения, или гауссова плоскость) находится в бесполевом пространстве, достаточно ограничиться прямолинейными траекториями, считая, что на входе в эту бесполевую область предшествующим электрическим полем сформирован волновой фронт семейства траекторий с определенными свойствами.

Итак, пусть обозначены: кривая у , r = r ( s ) — волновой фронт семейства траекторий на плоскости, s — естественная параметризация кривой. Траектории ортогональны к кривой γ и прямолинейны. Огибающей семейства нормалей к кривой γ , т. е. каустикой рассматриваемого семейства траекторий, является эволюта [6]

r ( s ) = r ( s ) + -1- n ( s ),            (3)

k ( s )

где

k ^{( s} ) =

d2r ds2

1   d² r

n ( s ) =--7

k ( s ) d s ²

— кривизна кривой γ, единичный вектор нормали к кривой γ в точке r(s) .

Допустим, что кривизна волнового фронта имеет экстремум в точке s0 и k'(s 0)=k\s 0)=... = k(1 -1)( s 0) = 0,      k(1)(s 0) * 0. (4)

Поместим начало системы координат XY в точку r(s0) , направив ось X вдоль вектора касатель-dr ной t = в этой точке, а ось Y вдоль вектора ds нормали n (s0) (см. рис.).

Используя формулы Френе [5], легко показать, что при выполнении условия (4) для эволюты (3)

r ‘ ( s 0 ) = r "( s 0 ) = ... = r ^{( 1 - 1)}( s 0 ) = 0,

Г 1 Y 1 )

^{r ( 1 )( s} 0 ) =|    ) n ^{( s} 0 ),

< ^{k V} s 0

r ^{( 1 +} 1) ( s 0 ) =

Г 1 у 1 + 1)                            г 1 Y 1 )

| I      n(s0) - 1k(s0)t(s0) | I kk s0                                                       s0

Поэтому в окрестности точки r ( s ₀) будем иметь

I * ⁽ ' ) =

/              ( 1 A ( ¹ )

=- TTTw k ( s 0 ) (?) ( s - s 0 ) ^{1 + 1} + O ( ( s - s 0 ) ¹ + 2 ) ,

(I +1)!       < k) s 0

1 Г 1

y ^{( s} ) = ^y 0 ⁺77 | 7 I ^{( s - s} 0 ) ^{1 +} O ( ( s - s 0 ) ^{1 + 1} ) .

1 ! V k y.

i

Здесь y0 = y (s0)=—-—=R (s0) — радиус кривизны 0        0    k(s0)

кривой γ в точке s ₀ .

Из соотношений (5) следует, что вблизи s ₀ имеем уравнения каустики:

:r ^{( s} ) = c_x ( ^{s - s} 0 ) ^{1 + 1},    ^{y ( s} ) ^{- y} 0 = c y ( ^{s - s} 0 ) ¹ .

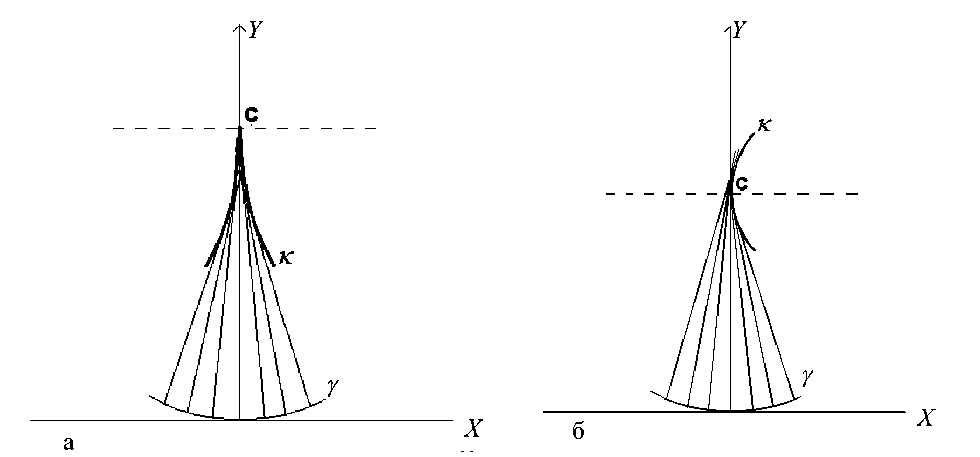
Каустики (кривые κ ) семейства прямолинейных траекторий вблизи точки фокусировки порядка l _.

a — четное значение l ; б — нечетное значение l . Точка C — точка фокуса, кривые γ — волновые фронты

В случае четного значения l каустика рассматриваемого семейства траекторий имеет при s = s 0 точку возврата (точка С на рис., а). Острие каустики направлено в сторону от волнового фронта, если его кривизна в точке s ₀ имеет минимум ( k ^{( l} ) ( s 0 ) >  0). Если кривизна имеет максимум в точке s ₀ ( k ⁽ l ) ( s 0 ) <  0), то острие направлено к волновому фронту. В частности, при l = 2 имеем полукубическую параболу: x = c_x ( s - s ₀ ) ³, y ^- y 0 = c y ( ^{s - s} 0 ) ².

Для случая нечетного значения l каустика изображена на рис., б. Она может располагаться как слева, так и справа от оси Y в зависимости от знака k ^{( l )}( s 0 ).

Заметим, что в случае осесимметричных систем для меридиональных траекторий реализуются только четные значения l : в силу указанной симметрии k ( s ₀ + A ) = k ( s ₀ - A ).

Из соотношений (5) легко получить зависимость от параметра s угла с осью Y траектории, проходящей через точку r ( s ) волнового фронта и касающейся каустики в точке r ( s ):

₊      d x /d y    . .     .

a ~tga =— /—= -k0(s -s 0) , ds  ds где kо = k (s0).

Координата точки пересечения траектории с гауссовой плоскостью — с плоскостью фокусировки (прямая y = y ( s ₀))

( - 1) ^{l + 1} ( 1 V ^l )

x = x - ( y - y ( s ₀))tg a =—j------ — a^l .   (6)

0         k о ^l ( l + 1Д k ) s о

Такой вид зависимости координаты точки прихода частицы в гауссову плоскость от угла наклона траектории в терминах оптики заряженных частиц [5] означает наличие в плоскости y = y ( s 0 ) фокусировки l -го порядка.

Таким образом, каустика для семейства прямолинейных траекторий на плоскости в окрестности его точки фокусировки нечетного порядка (фокусировка первого, третьего и т. д. порядков) имеет вид, изображенный на рис., б. Для случая фокусировки четного порядка каустика имеет вид, изображенный на рис., а. В этом случае каустика имеет точку возврата.

КЛАССИФИКАЦИЯ ОСОБЕННОСТЕЙ ПОЛЯ ТРАЕКТОРИЙ

Коснемся теперь вопроса о классификации особенностей поля траекторий, связанных с фокуси- ровкой l -го порядка, в терминах теории катастроф [1]. Для этого рассмотрим плоскость y=y (s0) + 5, близкую к гауссовой. Используя соотношение (6), с учетом малости угла α траектории с осью Y имеем для координаты точки пересечения траектории с этой плоскостью x (a, 5) = cla+1 + 5a. (7)

Здесь введено обозначение cl =

( - 1) ^l k 0 ^l ) ( l + 1)! k 0 ⁺ 2

k ₀ ^{( l )} — значение первой отличной от нуля производной кривизны волнового фронта в критической точке в соответствии с (4).

Критические углы траекторий определятся из условия dx/da = 0, откуда для четного l и при условии 5c < 0 имеем два значения ac = ±(-5/ ((l +1) Cl ))Vl(9)

и для нечетного l — одно значение критического угла ac =-(5 ((l +1) Cl ))Vl.(10)

Каустики определятся из условия

,x ^{( 5} ) = x(a,⁵ )| _a=_a , откуда

x(5) =     ac5.(11)

l + 1

Для четных значений l вещественная каустика имеет две ветви и расположена в области значений δ , противоположных по знаку коэффициенту c_l .

Производящая функция или версальная деформация особенности [1], соответствующая фокусировке l -го порядка (соотношение (7)), содержит l существенных внешних параметров (коразмерность особенности равна l ) и при l >  1 имеет вид

f ( a , X₁, ^ ,X_l ) = a^{l + 2} + X₁a + X 2 a ^{- 1} + „. + X_la. (12)

Параметры X , ^ , X_l образуют пространство каустики. В соответствии с зависимостью (7), для фокусировки l -го порядка

X = X ₂ = „. = X_{l - 2} = 0;

; - ^l + ²       -

^X l - 1 =       ⁵ ;   ^X l =

2 c_l

-

l + 2

x . c_l

Для фокусировки первого порядка ( l = 1) вер-сальная деформация f (ос , X ) = a ³ + Xo c , где a = a + 5 2 c ₁, имеет один существенный внешний

3 <    52) _       .         .   „ параметр X =--x + — . Точка фокуса X = 0 в ci I    4 ci )

терминах теории катастроф [1] является точкой типа "складка". Это условие определяет параболу x + 5 ²/4 с 1 = 0 в пространстве координат ( x , 5 ), на которой реализуется фокусировка первого порядка и которая является каустикой.

Для фокусировки второго порядка версальная деформация содержит два существенных внешних параметра, которые связаны с координатами в плоскости ( x , δ ) соотношениями (13). Точка фокуса X = X 2 = 0 — точка фокусировки второго порядка, является точкой "сборки" [1]. Каустика данной особенности — полукубическая парабола 8X 3 + 27X 22 = 0. Ее точки вне фокуса — точки "складки". В этих точках реализуется фокусировка первого порядка.

В случае фокусировки второго порядка две пространственные координаты ( x , δ ) полностью описывают особенность, ее версальную деформацию и пространство каустики, которое в данном случае является двумерным.

Для фокусировки третьего порядка ( 1 = 3) версальная деформация содержит три существенных внешних параметра. Пространство каустики трехмерно. Точка фокуса X = X ₂ = X 3 = 0 — точка фокусировки третьего порядка, является точкой типа "ласточкин хвост" [1]. Каустика представляет собой сложную поверхность в трехмерном пространстве. В нашем случае в доступном нам пространстве координат ( x , δ ) мы наблюдаем лишь сечение этой поверхности плоскостью X = 0, которое имеет вид 27 X 24 + 80 X 3 = 0 и которое схематично изображено на рис., б. Точки этой каустики вне фокуса являются точками "складки". В этих точках реализуется фокусировка первого порядка.

В случае фокусировки четвертого порядка ( 1 = 4) точка фокуса X = X 2 = X 3 = X 4 = 0 — точка типа "бабочка" [1]. Каустика такой особенности — трехмерная гиперповерхность в четырехмерном пространстве. Каустика в пространстве ( x , δ ) — сечение этой поверхности плоскостями X = 0 и X = 0, которое схематично изображено на рис., а. Точки этой каустики вне фокуса являются точками "складки", где реализуется фокусировка первого порядка.

Плотность траекторий I ~ ( d xda a ) 1 на каустике обращается в бесконечность. Используя формулу (11), легко получить порядок особенности:

– в плоскости фокусировки

I ~ a ~¹ ~ x~^{1 ( 1 + 1)} при а ^ 0, x ^ 0;

- в плоскости y = у 1 вблизи фокуса ( y 1 ^ y ( s ₀))

I~ (а - а1)-1~(x - x1)"1/2, а ^ а1, x ^ x1, где x1 — координата пересечения каустики плоскостью, α1 — соответствующий угол траектории.

Независимость порядка особенности от l вне фокальной точки означает однотипность точек каустики — как уже отмечалось выше, все точки каустики кроме, может быть, фокальной — точки "складки".

ЗАКЛЮЧЕНИЕ

Задачи электронной оптики — это, как правило, исследование особенностей отображения двумерных многообразий (например, направление луча, выходящего из заданной точки, представляется некоторой областью на единичной сфере) на двумерные (например, плоскость фокусировки). Устойчивыми особенностями таких отображений, согласно теореме Уитни [1], являются только "складка" и "сборка". Все остальные "малым шевелением" распадаются на эти две. Это означает, в частности, что фокусировка третьего и более высокого порядков в реальных системах недостижима, мы лишь можем приблизиться к ней, максимально сжав каустическую структуру из точек "складки" и "сборки".