Остаточная влажность материала при валковом отжиме

DOI:

Основной задачей процесса валкового отжима является обеспечение требуемой технологическим процессом остаточной влажности отжимаемого материала. Поэтому при исследовании процесса валкового отжима любых материалов, одной из основных задач является определение аналитической зависимости остаточной влажности от параметров процесса валкового отжима.

Исследования по моделированию остаточной влажности отжимаемого материала проводятся в трех направлениях.

Первое ‒ экспериментальное, строится на основе опытных данных, с применением методов математической статистики и планирования эксперимента, получаемых в виде эмпирических или регрессионных зависимостей [1-3].

Второе ‒ экспериментально-теоретическое, строится в результате теоретического исследования на основе экспериментально полученных эмпирических зависимостей [4, 5].

Третье ‒ теоретическое, строится в результате теоретического исследования на основе изучения гидравлических явлений, происходящих в зоне контакта валков с отжимаемым материалом [6-10].

Анализ литературы показал, что модели остаточной влажности, полученные экспериментальными методами, используют в основном с учетом технологического назначения. Степень дальнейшего применения формулы остаточной влажности, полученной экспериментально-теоретическим методом, зависит от использованных в ней эмпирических зависимостей. Корректная модель остаточной влажности, полученная теоретическими методами, в настоящее время отсутствует. Имеющиеся отдельные модели могут быть использованы в исследованиях частных случаев валкового отжима.

В работе [10] были определены аналитические зависимости, описывающие остаточную влажность отжимаемого материала для симметричного двухвалкового модуля. В целях дальнейшего развития теоретических представлений, как в работе [11], объектом исследования служит обобщенный двухвалковый модуль, в котором валки расположены относительно вертикали с наклоном справа под углом β , имеют неравные диаметры с эластичными покрытиями ( D_x ^ D ₂) , слой волокнистого (обрабатываемого) материала имеет равномерную толщину δ и подан с наклоном вниз относительно линии центров под углом γ (рис. 1).

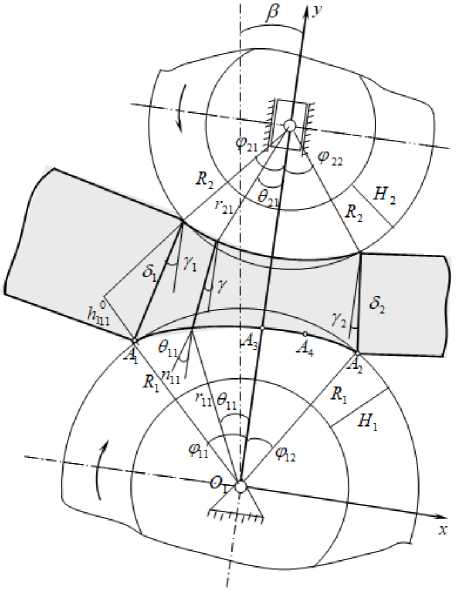
Рисунок 1. Схема двухвалкового модуля отжимных машин. Figure 1. Scheme of a two-roll module of squeezing machines.

МЕТОДЫ

Кривая контакта нижнего валка (кривая A 1 A 2 ) состоит из двух зон A A и

AA .

В зоне A A происходит сжатие волокнистого материала и покрытия валка, а

^A 3 ^A 2 ^–

восстановление деформации.

Сначала рассмотрим процесс фильтрации жидкости в зоне A A .

В зоне сжатия для рассматриваемого двухвалкового модуля имеем [1]:

r

R 1

^{1 + k} 11 ^ 11 к

1 + k 11 ^ 11

^cos(^ 1 + Y i )

cos(^n + Y) )

-(Ф11 + Y1) ^ °п + Y ^ 0,

,    k 11^11 R r =  --:——

1 + k ii ^ i

sin O, ^{L cos} Ф 11---2^1

i         cos O i

.

m 11 H 1 8т( ф _п + Ф ₂ 1 ) где ^k 11 —    *

^m 1 ^ 1 ^sin⁽ Ф 21 ^- Y 1 )

A_X 1 m ;1 ( A / 11 ) ср - ( A 1 (1 - m 11 ) - 4 *1 (1 - m ^)) ^ Q

An m _n(A / 11 ) ср + ( 4 11 (1 - m _n) - A * (1 - m * )) H 1 ;

0    * ^— Y 1 ) .               sm2( ^ _u + / 1 )

h ii = ⁵i               ;;   ^{( A} l ii ) ср = R i ' ¹ — ,

s*_u + ф 21 )               (     ²⁽ ^ 11 + y D )

здесь m, _t — коэффициент упрочнения точек эластичного покрытия нижнего валка при сжатии, m ** — коэффициент упрочнения точек мокрого материла при сжатии.

В зоне A A мокрый материал сжимается, поэтому жидкость переходит из нее в покрытие валка вдоль полярного угла [5, 11].

Как известно [11], количество удаленной жидкости, протекшей вдоль кривой контакта валка, может быть определено выражением dG = Bpu9dh,

где B — ширина мокрого материала; р — плотность жидкости; ие — скорость фильтрации в направлении 9.

В зоне сжатия A A скорость фильтрации u описывается формулой [11]:

u n s =^{— Ь} 11 ⁽( ф ц ⁺ Y 1 ) 3 ^{+ ( 9} 11 ⁺ Y ⁾³⁾,  — ( Ф 11 + Y 1 ) ^ 9 11 + Y ^ 0 ,                ⁽⁴⁾

_{где b =} v m ^R 1 ^COS( Ф 11 ⁺ Y 1 )      _h 0 _₅ ^Sin( ф 21 ^— Y 1 )

• ^{11    3 h} H^{(1 +} k 1 Л 1Х^{1 +} k 11 Л 1^cos( Ф 11 ⁺ Y 1 )),      ^{11     1 sin} ( ф 11 ⁺ ф 21^).

На этом участке деформация мокрого материала выражается равенством h11 = R1 cos(Ф11+ Y) — r11 cos(911 + Y).

Отсюда, с учетом выражений (1) и (2), находим dh11

d ( 9 11 + Y )

R ¹—^{sin( 9} 11 + y ) ~   R ^^{( 9} 11 ⁺ Y ) -

• 1    + k j ^               1 + k_xx

Согласно формулам (3), (4) и (5), имеем dG„ = — PBRbY ((Ф11 + Y1)3 + (911 + Y )3 )(9.1 + Y) d (9» + Y) -(6)

^{1 + k} 11 ^ 11

После интегрирования выражения (6) получим

G =—  pBR1 b11  (2(  + y )5 + 5(ф + л )3(9 + y )2) + C r

• 11     10(1 + k ^H)     11              11    1     1111

Постоянную C находим по условию G ( - ( ϕ + γ )) = 0 :

^C 11 ⁼

ρBR 1 b 11 10(1 + k 11 λ 11 )

3( ϕ ₁₁ + γ ₁ ) ⁵ .

Тогда имеем

G 11 = α 11 (3( ϕ 11 + γ 1 )⁵ - 2( θ 11 + γ )⁵ -5( ϕ 11 + γ 1 )³( θ 11 + γ )²),             (8)

ρv BR ² cos( ϕ + γ )

.

где  -( ϕ + γ ) ≤ θ + γ ≤0, α =           ^{m 1     11   1}

• ^{11    1     11               11}   30 h 1 ⁰ 1 (1+ k 11 λ 11 )² (1+ k 11 λ 11 cos( ϕ 11 + γ 1 ))

Формула (8) определяет закономерности изменения удаленной жидкости, протекшей через зоны сжатия A A .

Количество удаленной жидкости, протекшей через зоны сжатия, определяется расходом в конечной точке A , то есть влажностью G (0) :

G11(0) = 3α11(ϕ11 +γ1)5.(9)

На участке A A зоны восстановления деформации скорость фильтрации u описывается формулой [10]:

u12θ=-b12((ϕ14+γ4)3 -(θ12+γ)3), 0 ≤θ12 +γ ≤ϕ14 +γ4 ,(10)

а деформация мокрого материала, выражением h12=r12cos(θ12+γ)-r12(0).

Тогда по формуле (3) с учетом выражений (10) и (11) находим dG12 = ρBR1b12 ((ϕ14 +γ4)3 -(θ12 +γ)3)(θ12 +γ)d(θ12 +γ).(12)

• 1    + k ₁₂ λ ₁₂

После интегрирования получим

G12=   ρBR1b12   (5(ϕ14+γ4)3(θ12+γ)2-2(θ12+γ)5)+C12.(13)

12   10(1+k λ )      14    4     12              1212

Согласно условию G (0) = G (0) = 3 α ( ϕ + γ )⁵ , находим C = 3 α ( ϕ + γ )⁵ .

Тогда имеем

G 12 =3 α 11 ( ϕ 11 + γ 1 )⁵+ α 12 (5( ϕ 14 + γ 4 )³( θ 12 + γ )²-2( θ 12 + γ )⁵) ,        (14)

ρv R ² cos( ϕ + γ ) где 0 ≤ θ + γ ≤ ϕ + γ , α =             ^{m 1     12   2}           .

• ^{12        14   4 ,    12}  30 h ⁰(1+ k λ )²(1+ k λ cos( ϕ + γ ))

Количество удаленной жидкости, протекшей через поверхности контакта зоны сжатия и первые участки зоны восстановления деформации нижнего валка, определяется расходом жидкости через выходное сечение зоны деформации, то есть влажностью G ₁₂ ( ϕ ₁₄ + γ ₄ ) :

G12(ϕ14 +γ4) = 3α11(ϕ11 +γ1)5 +3α12(ϕ14+γ4)5.(15)

На участке A A зоны восстановления деформации скорость фильтрации u описывается формулой [12]:

u129 =-b12((^14 + Y4)3 - ф12 + Y)3), Ф14 + Y4 ^ 612 + Y < Ф12 + 72.

а деформация мокрого материала, выражением h12 =r12cos(θ12+γ)-r12(ϕ14+γ4).

Аналогично равенству (12), имеем dG12 = ρBR1b12 ((ϕ14+γ4)3-(θ12+γ)3)(θ12+γ)d(θ12+γ)

1 + k ₁₂ λ ₁₂

или после интегрирования и использования условия G (0) = 3 α ( ϕ + γ )⁵ получим

G ₁₂ = 3 α ₁₁ ( ϕ ₁₁ + γ ₁ )⁵ + α ₁₂ (5( ϕ ₁₄ + γ ₄ )³( θ ₁₂ + γ )² -2( θ ₁₂ + γ )⁵),               (18)

где   ϕ ₁₄ + γ ₄ ≤ θ ₁₂ + γ ≤ ϕ ₁₂ + γ ₂ .

Обобщая формулы (14) и (18), получаем

G ₁₂ = 3 α ₁₁ ( ϕ ₁₁ + γ ₁ )⁵ + α ₁₂ (5( ϕ ₁₄ + γ ₄ )³( θ ₁₂ + γ )² -2( θ ₁₂ + γ )⁵),              (19)

где   0 ≤ θ ₁₂ + γ ≤ ϕ ₁₂ + γ ₂ , ϕ ₁₄ + γ ₄ = ς ₁( ϕ ₁₂ + γ ₂), 0 < ς ₁ ≤ 1.

Таким образом, закономерности изменения удаленной жидкости, протекшей через поверхности контакта нижнего валка, описываются формулами (8) и (19).

Современные инновации, системы и технологии //

Modern Innovations, Systems and Technologies

Количество удаленной жидкости, протекшей из материала через поверхности контакта нижнего валка, определяется расходом ее в точке A , то есть влажностью

^G 12^{( ф} 12⁾ •

G 12 ⁽ Ф 12 + Y 2 ) = ^{3 a} 11 ⁽ Ф 11 + Y 1^{) 5 + a} 12 ⁽⁵⁽ Ф 14 ⁺ Y 4^{) 3 (} ^ 12 ⁺ Y 2^{) 2 - 2(} Ф 12 ⁺ Y 2 )^$ ) •           ⁽²⁰⁾

Закономерности изменения и количество удаленной жидкости, протекшей через поверхности контакта верхнего валка, определяем аналогично.

Они имеют вид:

	G 21 = a 21 (3( ^ 21 - Y 1 )5 -2( ^ 21 - Y )5 - 5 ф - Y 1 )3( 6 — Y ) 2 ),                (21) pv m BR 2 2 cos( ^ 21 - Y i )
где	( ф^   Y ) — 6-   Y — 0,    a =                                         , 21   1     21             21   30 h^ \(1 + k2Л. 1) 2 (1 + k2Ai cos ^ 21 - y )) G 22 = 3 а 21( ф 21 - Y 1 ) + а 22(5( ф 24 - Y 4 ) ( 6 22 - Y ) - 2( 6 22 - Y ) ) ,                   (22)
где	0 — 6 22 - Y — Ф 22 - Y 2 ,   Ф 14 - Y 4 = ^ 2 ( Ф 22 - Y 2 ), 0 <  ^ 2 — 1; a  =__________ Vm PR 22COS ^ 22 - Y 2 ) __________ 22   3 0 h ’2 (1 + k22A 2 )2 (1 + k 2 2 A 2 cos( ^ 2 - Y ))" G 22( ф 22 - Y 2 ) = 3 а 21( ф 21 - Y 1 ) + а 22(5( ф 24 - Y 4 ) ( ф 22 - Y 2 ) - 2( ф 22 - Y 2 ) ) •           (23)

Количество удаленной жидкости из обрабатываемого материала в процессе отжима равно сумме количества жидкости, удаленной через кривые контакта нижнего и верхнего валков:

G yd = ^{3 а} 11^{( ф} 11 ⁺ ^ ^{+ а}12⁽⁵⁽ Ф 14 ^{+ Y} 4^{)3( ф} 12 ^{+ Y} 2⁾² - ^{2( ф} 12 ^{+ Y} 2^{)5) +}

^{+ 3 а} 21^{( ф} 21 - ^Y 1^{) 5 + а} 22^{(5( ф} 24 - ^Y 4^{) 3 (} ^ 22 - ^Y 2^{) 2} - ^{2( ф} 22 - ^Y 2^{) 5 )} •                 ⁽²⁴⁾

При известном количестве удаленной жидкости, удаленная влажность из мокрого материала при отжиме, определяется выражением [11]

W. = — — 100%,                             (25)

УД  PBVm где v - скорость материала.

При валковом отжиме имеет место равенства [11] W 0_cm = 1^_ач — W_yg , где W_ocт’ Whoч - остаточная и начальная влажность отжимаемого материала, соответственно.

Из выражений (24) и (25) следует, что остаточная влажность валкового отжима волокнистых материалов определяется выражением:

^W ocm = W Ha4 --1^ ^{(3 a} 1M1 + Y 1 ) 5 + « 12⁽⁵ ( ^ 14 + Y 4^{) 3} ( Р 12 + Y 2^ - ²⁽ ^ 12 + Y 2 Л ⁺ ρ Bv_ь

^{+ 3 а} 21 ( ^ 21 - Y \ f ^{+ а} 22⁽ 5( ^ 24 - ^Y 4^{) 3}( ^ 24 - ^Y 2^{) 2} - ² ( ^ 22 - ^Y 2^ Т) .             ⁽²⁶⁾

РЕЗУЛЬТАТЫ

Таким образом, определена аналитическая зависимость (26), описывающая остаточную влажность отжимаемого материала.

ВЫВОДЫ

• 1.    Разработаны математические модели закономерностей изменения удаляемой жидкости в зоне контакта и остаточной влажности мокрого материала в процессе валкового отжима.

• 2.    Из анализа расчетных данных и графиков (рис. 2) следует:

• •    количество удаленной жидкости в начале зоны сжатия растет быстрее, что связано с быстрым ростом деформации сжатия мокрого материала. Затем темп роста удаленной жидкости намного понижается, а под конец зоны сжатия удаленная жидкость стабилизируется, что связано с понижением деформации сжатия мокрого материала.

• •    закономерности изменения удаленной жидкости в зоне восстановления деформации зависят от числа ( [ = ^0,4 = 0,74, определяющего положение точки, где жидкость меняет направление. При 0 < ^ < 0,74, удаленная влажность после отжима будет меньше, чем в конце зоны сжатия. При этом происходит обратное впитывание влаги мокрым материалом из покрытия валка. При 0,74 <  ^ [ <  1, удаленная влажность после отжима будет больше, чем в конце зоны сжатия. При этом в начале зоны восстановления деформации жидкость перемещается из покрытия в мокрый материал, а в конце происходит обратное впитывание влаги из покрытия валка, причем

количество удаленной жидкости из мокрого материала в зоне восстановления деформации будет больше, чем впитываемой. При значении <^ = 0,74 количество удаленной влажности при отжиме равняется количеству удаленной влажности в конце зоны сжатия, то есть количество удаленной и впитываемой жидкости в зоне восстановления деформации будет равным.

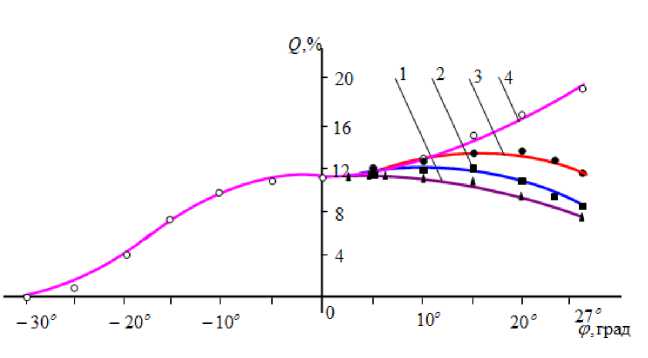
Рисунок 2. Графики изменения удаленной жидкости, протекшей через кривой контакт нижнего валка: 1                     1                      3 л

1-^14 - ^12’ 2-^и - —^12; 3 “ ^14 — ^^12 ’ 4 — ^14 — ^12 •

Figure 2. Graphs of the change in the removed liquid flowing through the contact curve of the lower roll: ,           1        „           1       1             3

1 ^14 ^— ^^12’ ^"^-Ф\^ -^ФМ! ³ ^14 ^— 4^’¹²’     ^14 ^— ^12"