Остаточные контактные напряжения после волочения бислойной трубы

• ¹    Волжский филиал Института металлургии и материаловедения им. А.А. Байкова РАН, г. Самара

• ²    Самарский государственный аэрокосмический университет

Построена математическая модель, позволяющая найти остаточное контактное напряжение после волочения бислойной трубы.

Остаточные напряжения на границе бислойных труб являются одним из наиболее важных показателей качества составных полуфабрикатов. Сжимающие напряжения способствуют сцеплению труб, а растягивающие напряжения препятствуют этому, вызывая отслаивание труб друг от друга.

В работах [1, 2] приведены теоретические зависимости для расчета остаточных напряжений для бислойной системы. Контактные напряжения находили, используя в [1, 2] решение задачи Ляме-Гадолина, в [2] теорему о разгрузке А.А. Илюшина. Расчетные значения контактных напряжений по разработанным методикам носят качественный характер, так как при теоретическом анализе процесс волочения был сведен к процессу редуцирования двух труб под действием радиального внешнего давления с осевым растяжением при различном удлинении наружной и внутренней труб. Кроме того, при вычислениях необходима дополнительная информация о усилии волочения, закономерностях упрочнения и деформации каждой трубы .

Для решения поставленной задачи в данной работе сделаны следующие допущения: деформация наружной и внутренней тонкостенных труб при волочении принималась как осесимметричная и безмоментная (рис.1); напряженное состояние плоское, а меридиональное оl и окружное ое - главные напряжения; трубные заготовки считаются несжимаемыми, трансверсально-изотропными, механические свойства в поперечном сечении одинаковы, но отличны от свойств в продольном направлении; упрочнение материалов труб изотропное и определяется в виде квадратичного полинома; на поверхности контакта наружной трубы с волокой действуют касательные напряжения, определяемые по закону Кулона. Массовыми и инерционными силами пренебрегаем. Рабочий канал волоки состоит из конического и радиусного участков, сопряженных между собой. Трубные заготовки разбиваются на узкие кольцевые элементы, число которых достаточно, чтобы считать процесс деформирования монотонным в пределах выделенного элемента. Взаимное перемещение труб при волочении в диапазоне коэффициентов вытяжек к < 1,2 отсутствует. Поверхность раздела бислойной системы в очаге совместной пластической деформации имеет вид прямо-

Рис.1. Схема волочения бислойной трубы линейного конуса с полууглом в • Напряженно-деформированное состояние кольцевых элементов трубы (рис.2) на коническом участке волоки длиной l описывается следующей системой уравнений:

dl dR       dt de, — —, deа — —, der — —;

l l     6 R           t

de_l + de ₆ + de_r — 0;         (2)

d ei — J      dde+ + de2 + 2^de6der; (3)

V1 - m²

o i — a ₀ + a₁1n X + a ₂( l n X )²;     ⁽⁴⁾

o1 —

M

1 - m ²

^o i

—

dei

[¹ I M

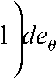
+ de ; (5)

M

o6—

o [f1 1 — M2 de IM ei

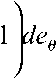
— de r

p — q • Cos (в — а) _ o6 • Cos а

t

R

;

— ( o ₆ Rt ) + o ₆ t + SR- + qR ( в — а ) — 0, (8) dR             sin а

где l , R, t ‒ текущие значения длины, радиуса и толщины стенки пластически деформируемой трубы:

R — R ₀ — l sin а ,            (9)

/ / R t _— t 0^ 0^vv0 , Rl  ^;

de_l , de ₆ , de_r , d e i - бесконечно малые приращения деформации и интенсивность прира-

щения деформаций; o l , o ₆ - компоненты напряжений и интенсивность напряжений; a ₀, a ₁, a ₂ - коэффициенты аппроксимации кривой упрочнения материала трубы; X - коэффициент вытяжки; M - коэффициент анизотропии; а - угол наклона образующей конического участка к оси волоки; p - контактное давление на стенки волоки, сопри-касаемые с трубой, q - контактное давление на границе труба-труба; f - коэффициент трения.

Радиусный участок волоки длиной l_р представлен в виде набора узких конических колец с углами

f R а _р — arccos —

'к — R

K- — +1

V ^R p

где R k - конечный радиус трубы, R _p - радиус кривизны радиусного участка.

На калибрующем участке волоки длиной l_кал принимали, что труба деформируется упруго согласно закона Гука, а нормальные контактные напряжения р постоянны по его длине. Дифференциальное уравнение равновесия имеет вид:

do l — /

dl     t p .

Таким образом, получена замкнутая система двенадцати уравнений для определения двенадцати неизвестных величин:

R , l , t , e ₆ , e_r , e_l , e i , o _i, o _l, o _t , p , q . Решение сис-

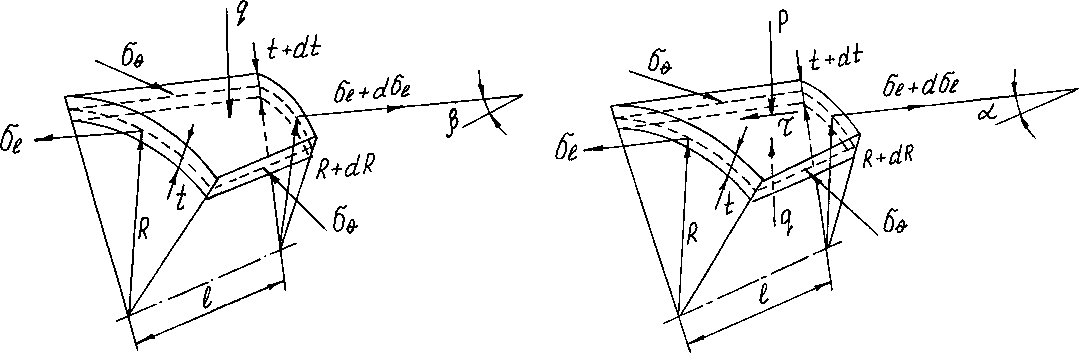
Рис.2. Напряженное состояние элементов наружной (а) и внутренней (б) труб

темы включает в представленной последовательности сводится к решению дифференциального уравнения статического равновесия (8) относительно независимой переменной R .

Процесс вычислений начинали с кольцевого элемента на входе в волоку, где напряжения и деформации считались известными и равными [3]:

с т l = 0,15 о _т , т _е = p = 0, е _е = e r = е l = 0, где О Т - предел текучести материала труб.

Напряженно-деформированное состояние в других элементах определяли от элемента к элементу при решении системы приведенных уравнений (1)-(12), записанных в конечно-разностном виде [4].

Из анализа априорной информации задавали начальное приближенное значение длины i- го элемента на отрезке

0,95 / ₀ <  1_t <  1,05 / ₀.

Точное значение длины 1_t , определяющего геометрию i -го элемента, находили методом дихотомии [4]. Другие параметры деформации элемента определяли по формулам (9) и (10).

Расчет проводили до определения переменной /_i с заданной точностью:

11"+1 - 1iN| < А 1 = 1 • 10 -9 м, где N+1, N - номер приближений для 1t.

Конечные деформации i-го элемента получили суммированием приращений де- формаций:

⁽ e i ) i = ( е\ - 1 ^{+ ( А e} i ) i ,

⁽ е е ) i = ⁽ e ₉ ) _t - 1 + ( ^А е е ) _t ,

( e r ) i = ⁽ e r ⁾ i - 1 ^{+ ( А} e r )„

⁽ е / ) i = ( е / ) . - 1 ⁺ ( ^А е / ) i ■

Расчет начинаем с определения параметров внутренней трубы.

Для описания закона распределения давления q по длине очага совместной пластической деформации на границе контакта труб использовали квадратичную зависимость q = aR2 + eR + c отображающую зависимость, полученную расчетом на ЭВМ в дискретных точках. Постоянные а, в, с находили по методу наименьших квадратов. Затем переходили к расчету параметров наружной трубы.

Границу раздела бислойной заготовки находили из условия минимума совместного усилия волочения Р в

■    = 0,

de где р - варьируемый параметр.

Рв = Рв1 + Рв 2, где Рв 1 и Рв2 - усилия волочения наружной и внутренней труб.

Р в 1 = о 1 П1 R 1 - 1 1 ) 1 1 ,

Рв 1 = о l 2 п (2R ₂ - 1 ₂) 1 ₂,

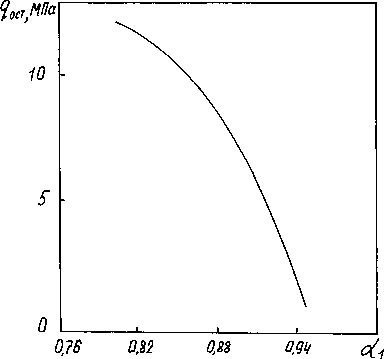
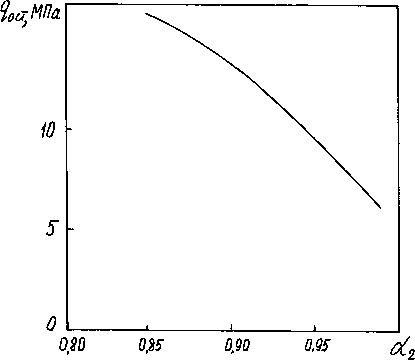
Рис.3. Остаточные контактные напряжения в зависимости от размеров наружной (а) и внутренней (б) труб

Г l 1 и cyl 2 - напряжение волочения наружной и внутренней труб.

Остаточные напряжения после пластической деформации в месте контакта труб при r = R2 определяли в виде разностей напряжений в пластическом состоянии и напряжений упругой разгрузки qост

2pE

ЦГ i i E 2 — ца 1 ₂ E , — 1 - ^ 2

E 2 Ц 1

V

1 + а?

1 - а 1 ²

- E J ц +

2,

1 - а 2

² 7

где Е₁ и Е₂ ‒ модули упругости материалов наружной и внутренней труб;

ц 1 и ц 2 - коэффициенты Пуассона материалов наружной и внутренней труб;

а 1 и а2 - коэффициенты толстостенности наружной и внутренней труб

RR а = ^-,а = 3

1 _{R 1}     2 _{R 2}

.

В качестве примера использования изложенной математической модели рассмотрен процесс волочения медной трубы из МЗ в отожженном состоянии с размерами 0 22 x 1,5 мм и вставленной внутрь нее с зазором трубы из алюминиевого сплава АД31Т с размером 0 18,5 x 1,0 мм. Результаты расчета q_ост приведены в таблице и на рис.3 и 4.

Величина остаточных напряжений, полученные расчетом на ЭВМ отличается от значений, полученных способом тензометри-рования [5] в пределах 18,6…21,3 %, что указывает на адекватность построенной матема-

Таблица. Сопоставление расчётных и экспериментальных данных q_ост

Методы исследования X =1,10 X =1,15 X =1,20 Тензометри-рование 20,97 27,26 33,83 Расчет на ЭВМ 17,09 22,54 26,61 тической модели.

Из графиков на рис.3 видно, что с уменьшением степени толстостенности наружной трубы остаточные контактные напряжения постепенно уменьшаются. Аналогичный характер изменения контактных напряжений имеет место с уменьшением степени толсто-стенности внутренней трубы. По абсолютной величине контактные напряжения убывают быстрее в зависимости от размеров внутренней трубы.

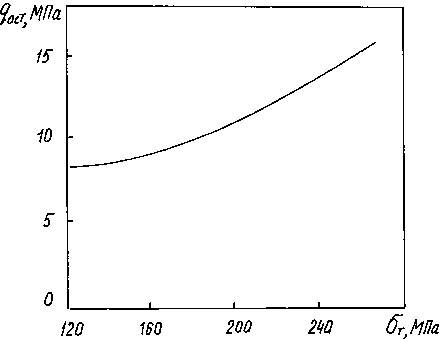
Из графиков на рис.4 видно, что с увеличением пределов текучести материалов сочленяемых трубных заготовок давление на границе контакта труб возрастает. По абсолютной величине контактные напряжения возрастают быстрее в зависимости от предела текучести внутренней трубы. Для получения плотного сцепления между трубами из однородных материалов необходимо, чтобы предел текучести материала внутренней трубы был больше предела текучести материала наружной трубы.

Предложенная математическая модель позволяет установить общие закономерности формирования остаточных контактных

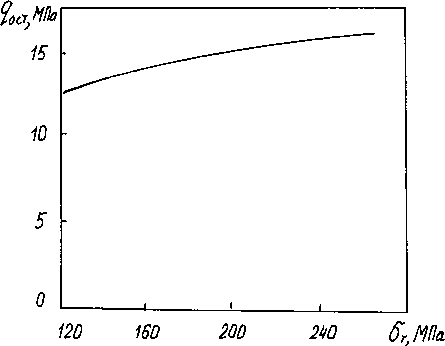
Рис.4. Остаточные контактные напряжения в зависимости от пределов текучести материалов наружной (а) и внутренней (б) труб

напряжений, необходимые для оптимального проектирования волочения бислойных труб.