Острая фокусировка света планарной градиентной микролинзой

Острая фокусировка света и преодоление дифракционного предела широко обсуждаются. Линзы и оптические элементы, имеющие возможность сфокусировать лазерный пучок в узкое пятно, соразмерное длине волны света или меньше неё, могут использоваться в задачах микроскопии, сопряжения волноводов, телекоммуникации, литографии, обработки материалов и т.д. Например, в [1–3] при моделировании было получено фокусное пятно с диаметром λ/2-λ/4. Одним из вариантов уменьшения фокусного пятна является использование поляризации света с радиальной симметрией [4, 5]. Другим способом уменьшения светового пятна является субволновая локализация света с помощью плазмонов на периодических структурах [6]. Таким образом можно получить острую фокусировку света, периодически повторяющуюся в пространстве. Узкая локализация света также может наблюдаться при распространении пучка в средах с анизотропией, например, состоящих из набора диэлектрических и металлических слоёв [7] или массива металлических проводников в диэлектрике [8]. В работе [8] получена локализация света в волноводной структуре шириной по полуспаду интенсивности FWHM = λ/9, а в [7] авторы получили очень острую локализацию света в продольной структуре с шириной по полуспаду интенсивности FWHM = λ/152 и FWHM = λ/268 по поперечным координатам. Однако для получения такой среды период чередования металлических (ε = -12,9) и диэлектрических (ε = 13,9) слоёв составил 13,2 нм. Такую среду сложно изготовить, кроме того, узкая локализация света остаётся внутри среды. В [9] показана возможность локализации света на поверхности наношара из металла или диэлектрика, находящегося на острие аксикона, в пятно с шириной FWHM = λ/400. Однако, такую конструкцию тоже сложно изготовить. Эффективность такой фокусировки авторы оценивают в 0,5 %, что может усложнить попытку экспериментально подтвердить результаты работы. Одним из перспективных способов преодоления дифракционного предела в исследовании нанообъектов является STED-микроскопия. В частности, авторы в [10] достигли ширины по полуспаду флуоресцирующей точки на изображении FWHM = λ/28. Широко распространены также фотонные кристаллы для фокусировки света [11, 12]. Например, в [11] авторы достигли ширины фокусного пятна в 0,26λ. А в [12], используя в качестве линзы одномерный фотонный кристалл, было получено фокусное пятно шириной FWHM=0,164λ.

Известно, что щель, ширина которой имеет порядок десятков нанометров, может служить для локализации и распространения в ней света, как в волноводе [13–15]. В двумерном случае было показано, что расположение щели в материале линзы в области фокусного пятна помогает значительно увеличить интенсивность света и уменьшить ширину фокуса. Так, в [15] в случае ТМ-поляризации получено фокусное пятно шириной FWHM = λ/28 и эффективностью 43 %. Однако возможность фокусировки света трёхмерной планарной микролинзой и влияние её толщины на возможность острой фокусировки света подобным образом не были исследованы. Перспективность такого способа острой фокусировки обуславливается возможностью локализации света с высокой интенсивностью на границе линзы, где узкое фокусное пятно может быть доступно для различных применений. Об этом и пойдёт речь в данной работе.

Моделирование

Свет распространяется в волноводе высотой H и шириной W , нанесённом на подложку из стекла. Показатель преломления подложки n = 1,5, волновод выполнен в кремнии, его показатель преломления n 0 = 3,47. Волновод оканчивается градиентной линзой длиной L , высота и ширина линзы равны таковым у волновода. Линза фокусирует свет на своей границе (рис. 1).

Градиентный показатель преломления линзы рассчитывался по формуле Микаэляна [16]:

n

( x ) = n 0(1 ch ^ 2L ^ )•

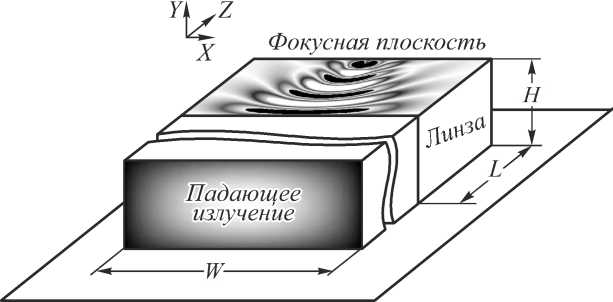
Рис. 1. Схема рассматриваемой задачи

Высота волновода и линзы H =0,8 мкм была выбрана исходя из возможности изготовления методами электронной литографии. Ширина линзы была принята W =4,8 мкм для удобства сравнения с результатами предыдущей работы [15], длина линзы L =2 мкм. Длина волны света λ = 1,55 мкм соответствует наиболее часто используемой длине волны в задачах телекоммуникации. Для наибольшего приближения результатов моделирования к возможному эксперименту световая мода, распространяющаяся в волноводе до линзы, рассчитывалась в программном пакете FIMMWAVE (Photon Design).

На рис. 2 представлен результат её расчета для линейно-поляризованного света с направлением электрического вектора вдоль оси X.

б)

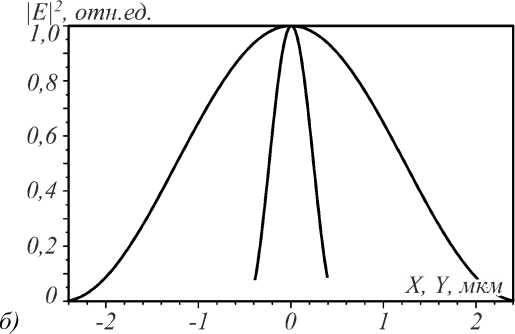
Рис. 2. Распределение интенсивности света |E|2, распространяющегося в волноводе до линзы, в плоскости XY (а, негатив), и его сечения вдоль осей X и Y (б)

Точка с координатами X = Y =0 на изображении совпадает с центром волновода. Как видно из рис. 2, при столь значительном различии между показателями преломления волновода и подложки сечение интенсивности света через центр волновода вдоль оси Y получилось практически симметричным относительно центра координат X = Y =0. Ширина падающего пучка при толщине волновода H =0,8 мкм равна FWHM x =2,13λ,

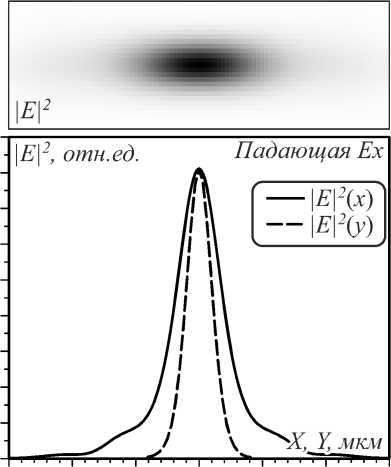
FWHM y =0,414λ. Прохождение света через линзу моделировалось методом FDTD, реализованным в программном пакете FullWAVE (RSoft Design). Наименьшая ширина фокусного пятна вдоль оси Х при этом получается при падающей волне Ey =1, Ex = Ez =0, его ширина по полуспаду интенсивности равна FWHM x =0,254λ вдоль оси X, FWHM y =0,19λ вдоль оси Y (рис. 3). При падающей волне Ex =1, Ey = Ez =0 ширина фокусного пятна по полуспаду интенсивности равна FWHM=0,268λ вдоль оси X, FWHM=0,15λ вдоль оси Y.

0 а)

\E\2, отн.ед.

Падающая Ey

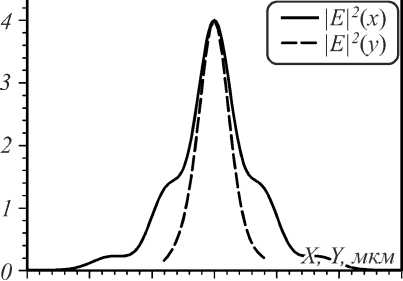
Рис. 3. Интенсивность света в фокусе градиентной линзы (негатив) для падающей волны Ex (а) и Ey (б) и сечения интенсивности вдоль осей X и Y через центр на оптической оси

Рассмотрим особенности фокусировки света при наличии щели на оптической оси линзы. Расположение щели и её размеры представлены на рис. 4.

Параметры щели выберем W 3 = H , W 2 = L . На рис. 5 показана зависимость ширины фокусного пятна по полуспаду интенсивности от ширины щели. Падающее поле – Ex = 1, Ey = Ez =0.

Из рис. 5 следует, что зависимость ширины фокусного пятна от ширины щели линейная и согласуется с аналогичной зависимостью в двумерном случае [15]. В рассматриваемом трёхмерном случае ширина фокусного пятна по полуспаду интенсивности получилась меньше примерно на 5 % по сравнению с двумерным случаем в работе [15]. На рис. 6 приведены основные энергетические характеристики фокусиров- ки света рассматриваемой линзой со щелью шириной в диапазоне W1∈(0, 200 нм).

За эффективность фокусировки примем отношение энергии внутри фокусного пятна (до первых минимумов) ко всей энергии, пришедшей в выходную плоскость линзы. Как видно из рис. 6, интенсивность сфокусированного излучения превышает интенсивность от обычной линзы в 4,8 раза при ширине щели 20 нм. Также видно, что эффективность фокусировки с уменьшением ширины щели увеличивается, что согласуется с ростом интенсивности в фокусе.

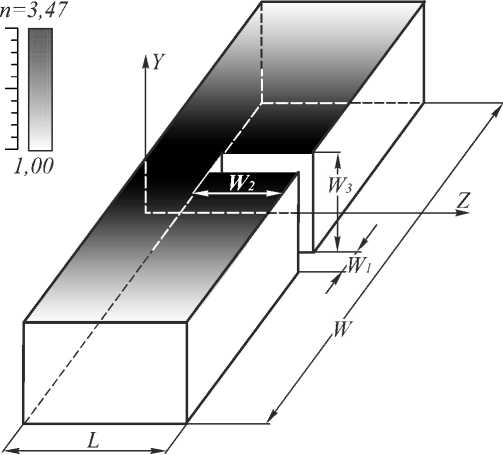
Рис. 4. Схема линзы со щелью на оптической оси

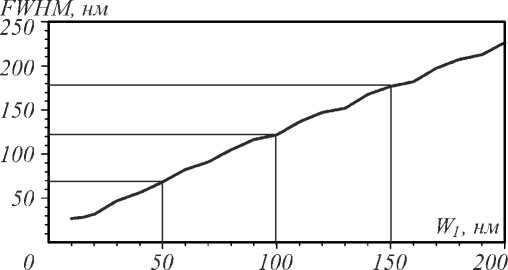
Рис. 5. Зависимость ширины фокусного пятна по полуспаду интенсивности от ширины щели W 1

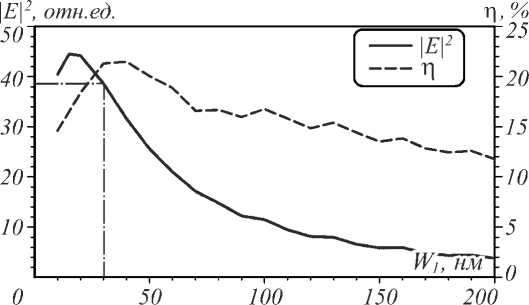
Рис. 6. Зависимость интенсивности |E|² на оптической оси и эффективности фокусировки света η от ширины щели W 1

Уменьшая длину щели, можно добиться ещё некоторой прибавки в интенсивности излучения в фокусе линзы. На рис. 7 показаны зависимости эффективности фокусировки и интенсивности на оптической оси от длины щели W2. Видно, что увеличить интенсивность в центре фокусного пятна на 37 % можно путём уменьшения длины щели до 200 нм, при этом эффективность фокусировки света также немного увеличивается и до- стигает η = 22,7 %. То есть увеличение в интенсивности в фокусе по сравнению с вариантом линзы без щели составляет приблизительно 6,5 раз. Ширина фокусного пятна при изменении длины щели остаётся неизменной, и в данном случае вдоль осей X и Y равна соответственно FWHMx=40 нм, FWHMy=280 нм.

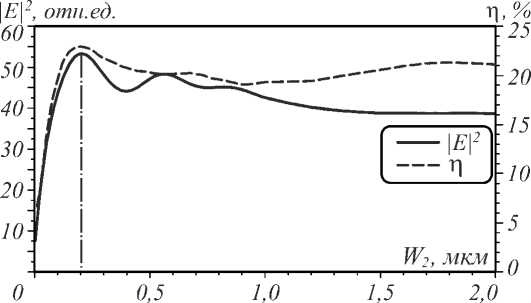
Рис. 7. Зависимость энергетических характеристик фокусировки от длины щели W 2 при ширине щели W 1 = 30 нм

На рис. 8 представлена зависимость интенсивности от глубины щели W 3 , при этом ширина и длина щели были зафиксированы на значениях W 1 = 30 нм, W 2 = 200 нм. Щель глубиной W 3 <  H размещалась в центре линзы, не достигая своими краями плоскостей линзы, граничащих с воздухом и подложкой.

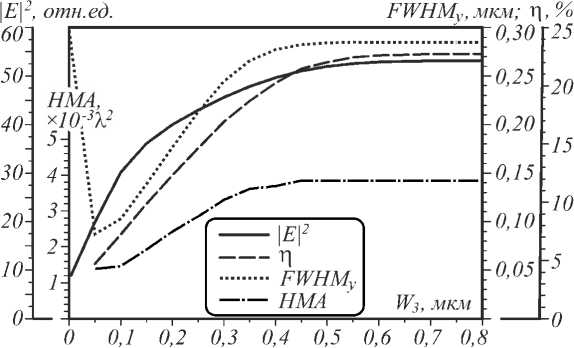
Рис. 8. Зависимость энергетических характеристик фокусировки от глубины щели W 3 при ширине щели W 1 = 30 нм и длине щели W 2 = 200 нм. На графике представлены интенсивность |E|² в центре фокусного пятна на оптической оси, эффективность фокусировки света η, ширина фокусного пятна вдоль оси Y FWHM y , площадь фокусного пятна HMA, приведённая в λ², где λ – длина волны света

Уменьшение глубины щели W 3 происходило таким образом, что центр щели оставался в центре линзы (на оптической оси, X = Y =0). Как показало моделирование, уменьшение этого параметра не приводит к дальнейшему росту интенсивности или эффективности фокусировки. При этом с уменьшением W 3 наблюдается уменьшение фокусного пятна вдоль оси Y начиная с W 3 =0,4 мкм и менее. Уменьшение глубины щели W 3 также влечёт уменьшение площади фокусного пятна, измеренное по половинному уровню (half maximum area – HMA). Для волновода толщиной 0,8 мкм оно составляет HMA=3,8· 10^–3 λ ². При уменьшении глубины щели до W 3 =0,05 мкм значение площади фокусного пятна падает до значения HMA= 1,3·10^–3 λ ². В отсутствие щели HMA=0,062 λ², что близко к значениям для острой фокусировки света аксиконом в свободном пространстве [17].

На рис. 9 представлен график зависимости эффективности фокусировки и интенсивности в центре фокусного пятна линзы от толщины линзы и волновода H .

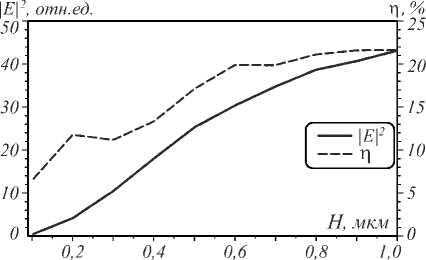
Рис. 9. Зависимость интенсивности в фокусе и эффективности фокусировки от толщины линзы и волновода H

Чтобы не учитывать возможные резонансные эффекты, длина щели в данном моделировании была равна длине линзы W 2 = L =2 мкм. Для получения данных на рис. 9 для каждой толщины H рассчитывались поля, распространяющиеся в волноводе и поступающие на вход линзы с помощью программного пакета FIMMWAVE. При этом производилась нормировка интенсивности в максимуме, то есть интенсивность электрического поля для различной толщины H одинакова на оптической оси, что даёт возможность сравнить возможности линзы по усилению интенсивности излучения в области фокуса. При увеличении толщины после значения H =0,8 мкм эффективность фокусировки выходит на уровень насыщения, равный η = 21..22 %, и останавливается в росте. Однако с уменьшением толщины волновода и линзы до H =0,6 мкм эффективность всё ещё остаётся в пределах 20 %. Полученные результаты дают представление о наилучших параметрах для наиболее эффективной фокусировки света линзой Микаэляна со щелью для получения минимального фокусного пятна, наибольшей эффективности и плотности энергии в фокусе линзы: H =0,8 мкм, W 2 =200 нм, W 1 =30 нм, W 3 = H . Интенсивность света в фокусе линзы с данными характеристиками представлена на рис. 10.

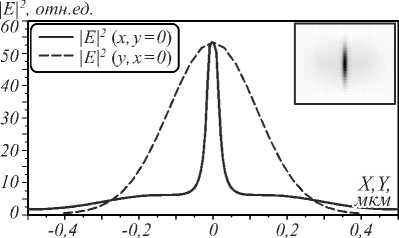
Рис. 10. Распределение интенсивности в фокусе линзы со щелью (негатив) и его сечения вдоль осей X и Y через центр

Поскольку градиентные линзы сложно изготовить, целесообразно градиентный профиль показателя преломления аппроксимировать ступенчатым бинарным профилем, например, в виде фотонно-кристаллической линзы.

На рис. 11 представлен профиль показателя преломления линзы в плоскости XZ, аналогичной той, результат которой рассматривался на рис. 10.

Z мои

, n=l n=3,47

-2-10  1  2

Рис. 11. Профиль показателя преломления фотонно-кристаллической линзы

Линза состоит из волновода с тем же материалом, показатель преломления которого n = 3,47, и отверстий в нём с показателем преломления n = 1. Моделирование показало, что при наличии щели зависимость ширины фокусного пятна вдоль оси X сохраняется такой же, как и для градиентной линзы, то есть ширина FWHM фокусного пятна шире W 1 на 15–20 %. Сохранился также и характер зависимости интенсивности фокусного пятна относительно длины щели: при аналогичных параметрах моделирования наибольшая интенсивность получается при длине щели в диапазоне W 2 = 180...200 нм. Однако с ростом количества рядов отверстий вдоль оси Z увеличивается интенсивность в фокусе линзы при отсутствии щели. Это способствует росту интенсивности при наличии щели оптимальной длины W 2 =200 нм, однако не пропорционально. Например, моделирование показало, что максимальная интенсивность по центру линзы при 6 рядах отверстий вдоль оси Z (максимальный диаметр отверстия – 333 нм) при отсутствии щели составляет I max = 1,78 отн. ед., в то время как при 8 рядах отверстий (максимальный диаметр отверстия – 250 нм, см. рис. 11) максимальная интенсивность возросла до I max =2,9 отн. ед. Минимальный диаметр отверстия в обоих линзах был ограничен в 30 нм. Максимальная интенсивность, полученная в результатах моделирования фокусировки света этими линзами при наличии щели на оптической оси с параметрами W 1 =30 нм, W 2 =200 нм W 3 = H составила 15,3 и 18,8 отн. ед. соответственно. Оптимальная длина щели в 200 нм для фотонно-кристаллического аналога градиентной линзы Микаэляна является наилучшей и для эффективности фокусировки света. Так, для линзы, изображённой на рис. 11, эффективность, измеренная до первых минимумов вокруг фокусного пятна, составила η = 30,2 %, что выше максимального полученного значения 22,7 % для градиентной линзы.

Заключение

В работе численно показана возможность фокусировки света планарной градиентной микролинзой со щелью в узкое пятно площадью HMA = 3,8·10–3 λ2 и минимальной шириной FWHM=0,026λ (λ/38). Эффективность фокусировки света до первых минимумов соста- вила 22,7 %. Ширина фокусного пятна определяется шириной щели на оптической оси линзы. Уменьшая ширину щели до 10 нм, можно добиться уменьшения ширины фокусного пятна вплоть до FWHM=0,027 мкм (λ/59), эффективность при этом упадет до η = 15 %. Чтобы упростить изготовление линзы, её можно представить в виде фотонного кристалла – массива отверстий в кремнии диаметром от 30 до 250 нм. В этом случае при ширине щели 30 нм и соответственно ширине фокусного пятна в поперечной плоскости 0,026λ эффективность фокусировки света составит η =30,2%.

Работа выполнена при поддержке Российского фонда фундаментальных исследований, гранты РФФИ 14-29-07133, 15-07-01174, 16-29-11698, гранта Президента РФ поддержки ведущих научных школ НШ-9498.2016.9.