От оксидов и силикатов до атома гелия

Конструирование нановеществ и устройств на их основе, исследование наноминерального мира предъявляют новые требования к теории химической связи, включая эволюцию связи в ряду: простая молекула — кластер — нанокристалл — кристалл. В данном ряду увеличивается сложность многоэлектронной системы. Чтобы понять законы усложнения, необходима безусловная уверенность в правильности описания простой системы. Понять природу химической связи, например в молекуле водорода, — это значит иметь пусть неточное, но правильное представление о движении электронов в ней. А простейшей многоэлектронной системой и пределом объединенного атома для молекулы водорода является, как известно, атом гелия. Поэтому предшествующие годы были посвящены исследованию химической связи в молекулах и основного состояния атома гелия путем анализа известных экспериментальных данных и сравнения их с общепринятыми теоретическими построениями.

Причиной такого рода исследований стало желание убедиться в правильности (и точности) или неправильности (или грубости) модели перекрывающихся неизменных атомов с целью применить ее самому и рекомендовать широкому кругу специалистов для определения прочности химической связи атомов или ионов на основе межатомных расстояний, установленных путем дифракционных измерений. В данной модели прочность (или энергия связи) пропорциональна глубине (или объему) области перекрывания атомов. Для этой цели необходимо иметь всего-то набор атомных и ионных радиусов. Строго квантовомеханически вычисляемые величины — это средние радиусы. Например, средний радиус атома водорода в основном состоянии, вычисляемый по формуле:

< г>=\. 5 /(2£)^1/2>         ⁽¹⁾

равен приблизительно 79 пикометрам ( Е — это энергия ионизации). Эти величины, вычисленные в соответствии с теорией многоэлектронных атомов, давно известны (например, атомные радиусы Вебера—Кромера). Однако их использование совершенно непродуктивно. Более приемлемы радиусы, ограниченные некоторым значением электронной плотности. Но и они не позволяют добиться необходимой для практических нужд точности (1—3 пикометра). Очень неплохих результатов удалось добиться с помощью эмпирических радиусов, выведенных мною на основе принципа «здравого смысла», в котором главную роль играет условие медленного изменения величины атомного радиуса у элементов от первой до восьмой группы в Пе-

Сравнение скоростей уменьшения различных атомных радиусов 2 / -элементов. R WC — радиусы орбитальных максимумов (Waber, Cromer, 1965), < R _CR> — ожидаемые значения (Clementi, Roetti, 1974), R _H — расстояния, на которых эффективный потенциал Кона—Шэма равен орбитальной энергии (Ghanty, Ghosh, 1996), R A and R _CR — эмпирические и теоретические радиусы

Взаимопроницаемые ионы кремния и кислорода в структуре кварца

риодической таблице Д. И. Менделеева. В качестве примера можно привести соотношение размеров ионов кремния и кислорода в структуре кварца и зависимость энергии сублимации кристаллов от степени перекрывания атомов.

Однако необходимо было доказать, что именно такие радиусы являются истинными. Для этого в свою очередь следовало доказать, что теория многоэлектронных атомов неверна. Это удалось сделать на примере простейшего многоэлектронного атома гелия. Погрешность теории обнаружилась в неправильном балансе потенциальных энергий притяжения и отталкивания, приходящихся на один электрон, который возникает в результате необходимой процедуры интегрирования уравнения Шредингера. Чтобы объяснить существо ошибки, не обойтись без краткого введения в теорию.

В основе нерелятивистской теории двухэлектронного атома с зарядом Z и бесконечной массой ядра, находящегося в центре координат, лежит стационарное уравнение Шредингера:

= ^(гь^),

с гамильтонианом (оператором суммы потенциальных и кинетических энергий электронов) H :

н = нх +н2 =

= -(|A1+Z/r1-l/r12)-

~l~k₂+Z/ ^2).

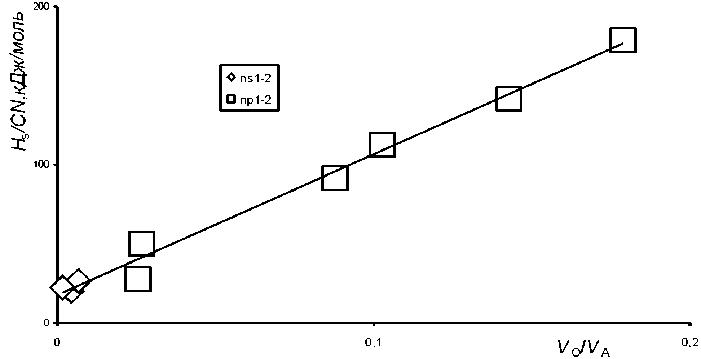
Корреляция между величинами энергии сублимации на одну связь H,/CNи относительным объемом области перекрывания сферических атомов VO/ VA некоторых гомоатомных веществ

Здесь используется атомная система единиц, в которой m _e = e =Й = = a ₀ = 1, m _e и e — это масса и заряд электрона, Й —постоянная Планка, а ₀ = 52.9177 пм — радиус Бора. Атомная единица энергии равна 27.2114 эВ = = 2625.500 кДж/моль. В уравнении (2) и формуле (3), которые обозначим как уравнение (2—3), r 1 и r ₂ — это координаты электронов, r 1 , r ₂ и r ₁₂ — расстояния от ядра до первого и второго электронов и между электронами, А — оператор кинетической энергии. Полная энергия E основного состояния равна сумме энергий ионизации электронов: E =—( E 1 + E2 ) < 0. Приближенная волновая функция основного состояния находится из вариационного условия минимума функционала:

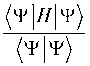
^ min = Е ,    (4)

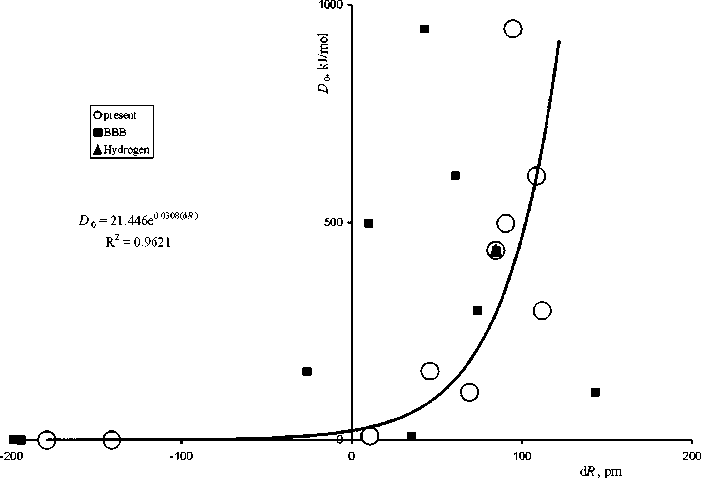
Зависимость энергии диссоциации гомоатомных молекул первого и второго периодов от глубины перекрывания атомов d R = 2< r > — R , где R — это межатомное расстояние. ВВВ — вид той же зависимости при использовании радиусов, вычисляемых согласно общепринятой теории (Bunge et al., 1993)

где скобки Дирака обозначают интегралы.

Дело в том, что для атома гелия стационарное уравнение Шредингера не может быть решено как задача на собственные функции и значения, т. е. подобно задаче для атома водорода. Поэтому изначально выбирается пробная функция с варьируемым параметром, которая подставляется в это уравнение. Простейшей вариационной функцией (в сферических координатах) является следующая:

уОЪГг^'МлЭч'гО'г^

Щс³/^¹^ ,   (5)

где к — варьируемый параметр. После интегрирования по координатам получается алгебраическое уравнение относительно варьируемого параметра, которое выражает закон «сумма кинетической и потенциальной энергий обоих электронов равна полной энергии атома»:

к² -2Zk+—k- Е .      (6)

Значение параметра к и, соответственно, конкретный вид волновой функции определяются с помощью процедуры минимизации трехчлена в левой части уравнения. Именно в данном алгебраическом уравнении потенциальная энергия притяжения, приходящаяся на одну частицу, в два раза больше, чем в исходном уравнении Шредингера. Причиной этого является то, что операция интегрирования по координатам, естественно, стирает информацию о различии в местоположениях электронов. В результате алгебраическое уравнение (6) описывает распределение потенциальной и кинетической энергии для некоторой единственной (несуществующей) частицы, в то время как в исходном уравнении Шредингера (2—3) их две. Вследствие избытка потенциальной энергии величина варьируемого параметра возрастает по сравнению с истинным. Средний радиус атома обратно пропорционален этому параметру. Поэтому он уменьшается. То же самое верно для всех атомов. Согласно теории, в формуле (1) для многоэлектронного атома Е есть полная энергия атома. В этом случае, например, радиус атома лития больше радиуса неона более чем в четыре раза. Исправление заключа ется в том, что уравнение Шредингера следует решать для одного из взаимодействующих электронов с оператором Н1 и энергией Е1, и, следовательно, в формуле (1) должно стоять значение первого потенциала ионизации атома. В результате разница радиусов атомов упомянутых лития и неона сокращается в два раза. Уже такое сокращение кардинально изменяет вид зависимости энергии диссоциации двухатомных гомоядерных молекул от глубины взаимопроникновения атомов. Уточнение волновых функций приведет к еще более точной форме данной зависимости.

Ценность проведенных теоретических исследований не сводится к поиску метода вычисления истинных радиусов атомов и ионов и анализу с их помощью межатомных расстояний. Полученные результаты имеют более глубокий смысл. На их основе уже сделан вывод о том, что решения стационарного уравнения Шредингера недостаточно для правильного описания состояния двух и более электронов как в атоме, так и в молекуле и кристалле. Данную проблему необходимо решать динамически. А это сопряжено с большими изменениями в представлениях и вычислительных методах. Надеюсь, что это составит программу действий на ближайшие годы.