Отбраковка "выбросов" и оценка параметров масс-спектрометрических сигналов для прецизионного изотопного анализа

Большинство масс-спектрометров, применяемых для изотопного анализа веществ в газовой и твердой фазах, имеют в своем составе автоматизированные измерительно-вычислительные системы различных типов. Основной целью настоящей работы является показать возможности повышение точности, надежности и производительности измерений путем введения в программное обеспечение вычислительных устройств нового поколения современных алгоритмов первичной обработки данных.

АЛГОРИТМЫ ОТБРАКОВКИ "ВЫБРОСОВ" В МАССИВАХ ДАННЫХ ИЗОТОПНЫХ МАСС-СПЕКТРОВ

Под "выбросами", или "ложными" элементами, понимают данные, сильно отличающиеся по величине от математического ожидания анализируемой выборки случайной величины. Плотность распределения данных случайных величин, в которых имеются "выбросы", f v обычно представляется в виде распределения Тьюки, которое записывается в следующем виде:

fv = f,(1 - а) + fга, где f1 — плотность распределения данных, в которых отсутствуют "выбросы", f2 — плотность распределения данных, которые являются "выбросами", а — относительное количество "выбросов" в анализируемой выборке данных. Например, если в анализируемой выборке данных содержится 10 % "выбросов", то а = 0.1, если 5 %, то а = 0.05. В случае нормального распределения анализируемых данных fv = N(m 1,°1)0 -а) + N(m2,02)а ,       (1)

где f , и f ₂ представляют собой функции Гаусса со средними значениями соответственно m ₁ , m ₂ и средними квадратичными отклонениями о 1 , о ₂. Очень часто "выбросами" являются данные, плотность распределения которых имеет среднее значение m ₂ = m ₁ , а средние квадратичные отклонения отличаются в к раз, то есть о ₂ = к о 1 . При этом число к может быть существенно больше 3. Для отбраковки "выбросов" наиболее простым и достаточно надежным методом является метод "3 о " (трех сигм). При наличии в выборке данных "выбросов" оценка значения величины о может быть искажена. Описываемые ниже алгоритмы показывают, каким образом в задачах масс-спектрометрического анализа газов в статическом режиме и в масс-спектрометрическом анализе веществ в твердой фазе производится отбраковка "выбросов" по методу трех сигм, в котором первоначальная оценка значения величины о производится особым способом.

Алгоритм с поочередным исключением измерений

Мы полагаем, что измерения являются линейной регрессией

y ( t^ = A + Bt, + W ( t i ), ( i = 1,..., n ) ,         (2)

где W ( t i ) — напряжение шума .

Из выборки, содержащей исходные результаты измерений, поочередно исключаются по одному, а затем по два измерения. При исключении двух измерений перебираются все комбинации пар. По оставшимся измерениям находятся методом наименьших квадратов коэффициенты А и В. По полученным массивам коэффициентов строятся линии регрессии и выбирается такая пара коэффициентов, которая дает наименьшую сумму квадратов отклонений S. По полученной S для каждого ис- ходного данного вычисляется значение его среднего квадратического отклонения от линии регрессии. В случае превышения отклонением значения 3S/(N - 1), где N — объем выборки, данное измерение заменяется значением, "лежащим" на линии регрессии. После этого по полученным новым данным вычисляются коэффициенты А и В. Данный алгоритм внедрен в программное обеспечение масс-спектрометров МИ 1201 ИГ [1] в Институте геологии рудных месторождений и в масс-спектрометре МИ 1201В в Объединенном Институте геологии, геофизики и минералогии СО РАН.

Алгоритм на основе метода квадрата минимального медианного остатка

Для того, чтобы использовать метод квадрата минимального медианного остатка [1], предлагается рассматривать преобразованные измерения z ( t i ) = У ( t i ) - Bt i и затем искать

I(B) = min {med[z(ti) - T(z(t1)...z(t„))2]}, где T(z(t1) ... z(tn)) — оценка параметра А, минимизирующая квадрат медианного остатка. Для нахождения В в качестве первого его приближения возьмем медианную оценку производной исходных измерений y(ti), т. е.

(

B = med

I

y ⁽ t i + 1 ) ^- y ⁽ t i - 1 ) ⁴ t i + 1 — t i - 1        ,

В дальнейшем выполняются операции по схеме оценки методом квадрата минимального медианного остатка для переменной z(ti ) = У(tm ) - B(ti - tm )» где У(tm ) = med(У(ti )) • нее квадратичное отклонение 8 = 1.48354 о2 .

• 6.    Вычисляем абсолютные величины остатков: r ( i ) = | z ( t i ) - A и проводим отбраковку "по-„              - С       r ( i ) 2

• 7.    Находим новые оценки параметров А и В и окончательную оценку дисперсии.

дозрительных измерений. Если ---> 3 , то i — отсчет "подозрительный". Этот отсчет заменяется отсчетом "лежащим" на линии регрессии для данного времени измерения. Полученный ряд измерений у(tj) обрабатываем по схеме наименьших квадратов У(z(ti)- A - Bti) ^ min.

Проверка данного алгоритма на моделях с различным отношением сигнал/шум показала результаты, представленные в табл. 1. На рис. 1 представлен пример восстановления линейного сигнала, в котором 50 % "выбросов".

Алгоритмы отбраковки "выбросов" в масс-спектрометрическом изотопном анализе веществ в твердой фазе

Отбраковка "выбросов" производится на следующих этапах проведения автоматизированного изотопного анализа веществ в твердой фазе:

• 1.    при определении среднего значения по результатам измерений на каждом из пиков спектра;

• 2.    при определении средних значений изотопных отношений по серии спектров;

• 3.    при определении средних значений изотопных отношений по нескольким сериям спектров.

• 1.    Строим вариационный ряд:

• 2.    Образуем следующие k разностей:

• 3.    Находим минимальную разность

• 4.    Находим оценку параметра А

• A = z( t th0+k+1) + z ( t th0) 2             .

• 5.    Находим дисперсию шума измерений через медианное отклонение о ² = ( A - z ( t _th0))² и сред

^{z (} t 1 ) < ^{z (} t 2 ) <  - < ^{z (} t k ) < - < ^{z (} t 2 k + 1 ); n = ² k ^{+ 1}

^A 1 = z ⁽ t k + 2 ) - z ⁽ t J;

A 2 = z ⁽ t k + 3 ) ^- z ⁽ t 2 );

A k = ^{z (} t 2 k + 1 ) ^{z (} t k )

A tho

Табл. 1. Результаты отбраковки "выбросов" алгоритмом на основе метода квадрата минимального медианного остатка

СКО шума, %	Заданное количество выбросов, %	Отбракованное количество выбросов, %
0	11	11
20	40	40
0_5	50	50
5^10	44	44
5^10	50	48
10^20	50	46
33	25	25

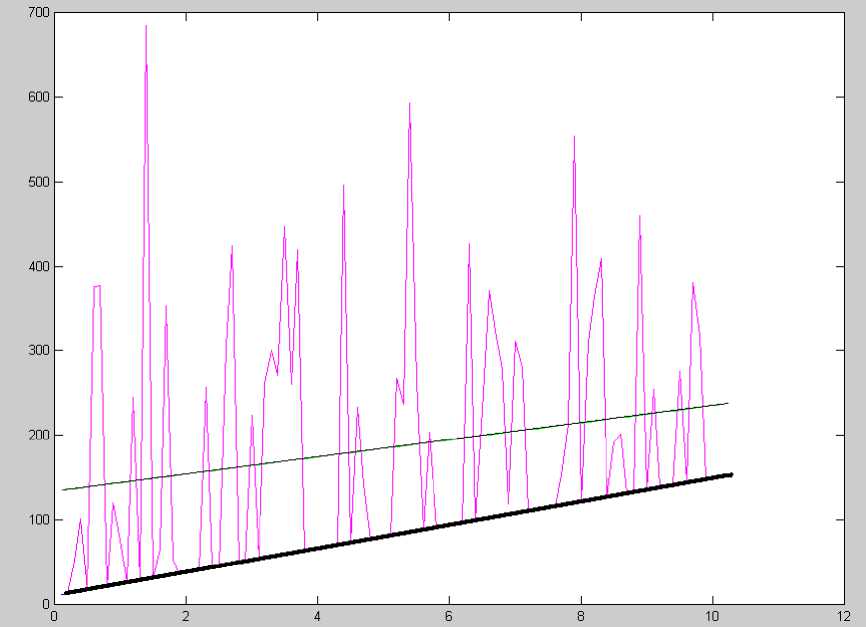
Рис. 1. Влияние односторонних "выбросов" на параметры линейного сигнала. Тонкой линией показан искаженный "выбросами" сигнал, а жирной — сигнал, восстановленный после удаления "выбросов"

Для каждого из этих этапов предлагается простая и достаточно надежная процедура отбраковки "выбросов".

• 1.    Строится вариационный ряд из обрабатываемых данных.

• 2.    Из всех данных отбрасывается а % данных, находящихся в верхней и нижней частях вариационного ряда, где а — априорный процент "выбросов" в соответствии с плотностью распределения, описанной формулой (1).

• 3.    По оставшимся данным определяется среднее значение m и среднее квадратичное отклонение 7 .

• 4.    Дальнейшая процедура отбраковки "выбросов" является стандартной по критерию к а , где к определяется по таблицам распределения Стьюдента в зависимости от объема выборки.

На рис. 2 показывается, какие из обрабатываемых данных участвуют в определении среднего значения m и среднего квадратичного отклонения 7. Проверка работы данного достаточно простого алгоритма на масс-спектрометрах МИ 1201Т и МИ 1320 [2] в Всероссийском геологическом институте показала возможность отбраковки до 15 % "выбросов".

Даммые, по которым определяются среднее и среднее квадратичное значения

п

Рис. 2. Упорядоченная выборка обрабатываемых данных, построенная в порядке возрастания чисел. Темным фоном показаны числа, которые не участвуют в определении среднего и среднего квадратичного значений выборки

НАСТРОЙКА НА ОПОРНЫЙ ПИК

rect ( t ) =

1,

1 1 ^ t ^ 1 2 ,

Время настройки на центр пика, выполняемой во всех масс-спектрометрах с дискретной ступенчатой разверткой, можно сократить при использовании описываемых ниже алгоритмов. Без применения этих алгоритмов время получения оценки положения середины пика при постоянной времени измерительной системы, равной 0.2 с, достигает 80 с (резистор в цепи обратной связи электрометрического усилителя имеет сопротивление 1012 Ом). В применяемых до сих пор алгоритмах необходимо проводить измерение 50–60 значений ионного тока в области предполагаемого положения центра пика при разных величинах напряженности магнитного поля [1]. Время, в течение которого удается проделать необходимое количество измерений, столь велико еще и по той причине, что для снижения влияния динамических ошибок перед измерением каждого нового значения ионного тока необходимо дождаться завершения переходных процессов в системах прибора. Необходимое для оценки положения центра пика количество исходных данных и, следовательно, общее время настройки можно существенно сократить, если найти модель пика, удачно (с точки зрения минимума средней квадратичной ошибки) описывающей пик. В этом случае можно оценить положение центра и другие параметры пика лишь по нескольким значениям ионного тока, примерно равномерно распределенным по области, где находится пик. А если при вычислениях учитывать динамические свойства измерительной системы, то становится возможным снимать значения (ионного тока), не дожидаясь окончания переходных процессов, что еще несколько снизит общее время оценки положения центра пика. Уменьшение времени работы программы позволяет снизить влияние нестабильных процессов в источнике ионов, ионно-оптической системе и в системе управления магнитным полем.

0, t <  1 1 или t >  1 ₂,

которая описывает влияние широкой щели. Такая композиция представляет собой примерно равномерную полосу в своей средней части, быстро спадает по краям и выражается следующим образом:

( i (t) = A Ф

t 2 t

V V

о2 J

+ Ф

_V ))

,

где Φ — функция Лапласа, А — масштабный множитель.

Графики функции i ( t ) (при t 1 = 60.9, t 2 = 108.5, A = 256.3, о = 7.5) и пика изотопа стронция 88 (Sr ⁸⁸) приведены на рис. 3.

Используя указанную модель, произведем оценку положения центра пика. Так как масс-спектрометр относится к классу так называемых линейных приборов [3], то выходной сигнал может быть представлен в виде свертки (при отсутствии шума и при пренебрежении дискретным характером измерений на конечном интервале)

^

I ( t ) = J h ( t — т ) i ( t )d T .

-^

Здесь t и τ — параметры времени при управлении напряженностью магнитного поля. Такой переход оказывается допустимым, т. к. напряженность магнитного поля в пределах одного пика можно считать линейной функцией от времени. Естественно, встает вопрос о восстановлении истинной зависимости i ( t ) по измеренным значениям I ( t ) решением уравнения (4).

Модели пика для изотопных масс-спектрометров

Качественно форму пика можно вывести до опыта из теоретических соображений. Поскольку обычно форма одиночного пика масс-спектрометра качественно близка к гауссовой кривой, можно в качестве модели одиночного спектрального пика использовать композицию функции Гаусса

s ( t ) = exp

V и прямоугольной функции

J

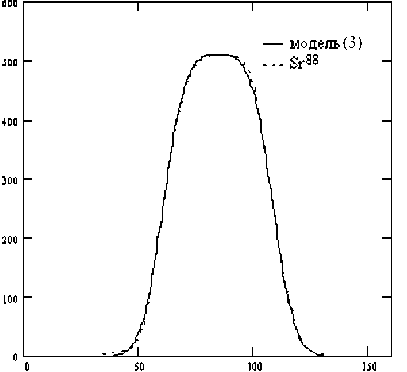
Рис. 3. Графики модели i ( t ) (3) (параметры указаны в тексте) и пика изотопа стронция Sr⁸⁸

Трудность состоит в следующем. Данные I ( t ) реально регистрируются с некоторой погрешностью, а задача (4) относится к классу обратных, некорректных в классическом смысле задач [3], поэтому возможно получение неустойчивого, осциллирующего решения. Действительно, если формально задачу (4) решать методом так называемой деконволюции с использованием преобразования Фурье, то в результате при практических вычислениях получается осциллирующая кривая, не являющаяся искомым решением [4]. Для нахождения устойчивых решений обратных задач в вычислительной математике наиболее мощными методами являются регуляризация по Тихонову и оптимальная фильтрация Винера [5]. Поскольку в регистрируемых данных масс-спектрометра I ( t ) неизбежно присутствует шум, то требование выполнения точного равенства (4) не имеет смысла и целесообразно искать приближенное решение, удовлетворяющее уравнению (4) с допустимой точностью. Кроме того, иногда интеграл (4) удается взять в общем виде. Тогда наиболее простым и логичным методом решения данной задачи является подбор параметров для аналитического решения интеграла (4) методом наименьших квадратов.

Используем в качестве первого приближения аппаратной функции, описывающей динамические процессы в измерительном тракте масс-спектрометра, апериодическую функцию h (t) = eA, t), (5)

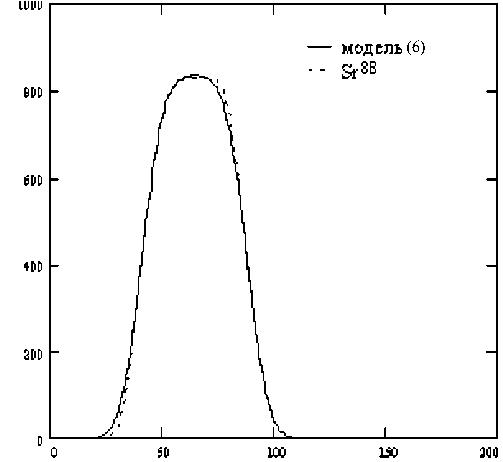
Рис. 4. Графики функции i ( t ) (6) (при условиях, указанных в тексте) и пика изотопа стронция Sr⁸⁸

где

n ( t ) =

1,

0,

t >  0, t <  0,

т. е. единичная функция

Хевисайда; a — параметр, характеризующий инерционность, имеет размерность с^–1.

Для аппаратной функции вида (5) и модели пика (3) решением интеграла (4) является уравнение

i ( t ) = A

f 1 a

V

«-a t A ^e—

a /

f f

Ф

t — t 1

^V2 J

f

—Ф

V

t ₂

—

t

О

График функции (6) (при А = 37.7, a = 0.09, t 1 = 41, t ₂= 88, о = 7.5) и пик Sr⁸⁸ изображены на рис. 4.

Степень близости модели к экспериментальным данным определялась по значениям невязок и по критерию X Пирсона [6].

Оценка среднего значения невязок для модели (3) и модели (6) не превышает 1.5 % от площади пика. Проверка соответствия моделей (3) и (6) экспериментальных данных по критерию X Пирсона показала ее правдоподобность с вероятностью 0.95. Для проверки моделей (3) и (6) экспериментальные данные регистрировались соответственно с интервалом времени 1.0 и 0.2 секунды.

Невязки, вычисленные для модели (6) носят периодический характер, что указывает на наличие колебательной составляющей в аппаратной функции. Следующая модель аппаратной функции, более точно описывающая динамические процессы внутри измерительной системы, — уравнение свободных затухающих колебаний

h ( t ) = e"^т sin to t n (t ), (7)

где to — круговая частота затухающих колебаний.

Аналитическое выражение свертки функций (3) и (7) получается довольно громоздким. Поэтому модельный пик проще вычислять непосредственно по формуле (4). Поскольку функция свертки (3) и (7) получается достаточно гладкой и без особенностей, нет необходимости в использовании сложных адаптивных алгоритмов интегрирования. Для вычислений можно воспользоваться одной из многоточечных прямых формул интегрирования, например Уэддля [7]. График функции (4) (при А = 780, 1 1 = 30, 1 ₂ = 78, ц = 7, а = 0.22, го = 0.050) и пик Sr⁸⁸, снятый с интервалом между измерениями в 0.2 с, представлены на рис. 5. На этом же рисунке показан пик, восстановленный рассматриваемым методом. На рис. 6 изображены модели пика при ( А = 90, 1 1 = 40, 1 ₂ = 86, ц = 7, а = 0.22, го = = 0.048) и пик Sr⁸⁴, снятый с интервалом между отсчетами в 0.275 с. Можно видеть, какое сильное влияние на снимаемые данные оказывает инерционность системы регистрации. Сравнение этой модели с экспериментальными данными показало,

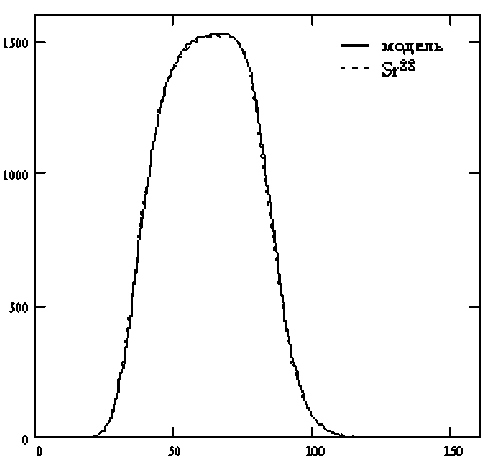
Рис. 5. График функции (4), снятый при указанных в тексте условиях, и пик изотопа стронция Sr ⁸⁸

• 1.    Практическую независимость от шумов точности оценки параметров пиков с использованием модели формы в диапазоне сигнал/шум от 50 и выше.

• 2.    Возможность восстановления параметров середины пика с погрешностью, допустимой для эксперимента при количестве проведенных измерений 5-6.

• 3.    Погрешность восстановления центра пика не превышает минимального шага системы управления разверткой.

ОБНАРУЖЕНИЕ ПИКОВ И ОЦЕНКА ИХ ПАРАМЕТРОВ В РЕЖИМЕ С НЕПРЕРЫВНОЙ РАЗВЕРТКОЙ

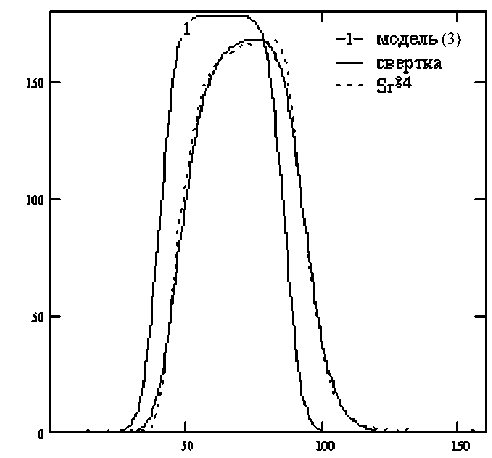
Рис. 6. Модель пика, вычисленная при указанных в тексте условиях, и пик изотопа стронция Sr⁸⁴

Обнаружение масс-спектрометрических пиков методом свертки экспериментальных данных с производными гауссовых функций

Теория и возможности метода обнаружения и оценки параметров масс-спектрометрических пиков методом свертки экспериментальных данных с производными гауссовых функций описаны в статье [10]. В настоящей работе приведем основные формулы и покажем на двух примерах возможности метода.

Частные производные второго и четвертого порядка для гассовых функций представляются в виде следующих функций:

S 2( t )=(1 — t ²/ ^ ₎²)exp(- / ² 2, ц , Т

S 4 ( t ) = (3 - 6 t ²/ ц >² + 1 ⁴/ ц 02 )ехр(- t ²/2 ц >² ).

Эти функции "подобны" пику в том смысле, что имеют экстремумы при t = 0.

Теперь рассмотрим свертки S 2 ( t ) и S 4 ( t ) с отдельно взятым пиком:

У 2^{( Т} ) = ^- A I ^еХР

-те у

t1

2 ц1

^

S 2 ( т - t )d t ,

/

те       /

У 4 ^{( т} ) = ^- A I ^еХР

-те

t1

2 ц1

^

V ( т - 1 )d t .

J

Взяв интегралы, получим:

что среднее значение невязок не превышает 4.8 % от площади пика. Так как модели пика представляют собой функции, нелинейные относительно своих параметров, то для их оценивания использовался итерационный метод Ньютона [8, 9].

Результаты проверки работы алгоритмов

Проверка работы алгоритмов показала:

У 2⁽ Т ) =

= А цп ^1/2 /[1 + ( ц / ц ₀)²]³² х

X (1 - т2 /(ц2 + ц 2)) х х ехр(-т2 /(ц2 + ц02));                  (11)

У 4^{( т} ) =

= А цл1² /[1 + ( ц / ц ₀)²]^5/2 х

х(3 -6т2 /(ц2 + ц0)) + т4 /(ц2 + ц2)2 х х ехр(-т 2/( ц2 + ц 02)).                      (12)

Из формул (11) и (12) следует:

— При т = 0 у ₂( т ) и у ₄( т ) имеют абсолютный максимум.

— у 2 (0)/ у 4 (0) = 1 + ( ц + ц о )².

— Если у обеих сверток в одной и той же точке имеются максимумы, то это значит, что на экспериментальной кривой в этом месте расположен пик, а в данной точке — его вершина.

Таким образом, производится обнаружение пика в спектре. Факт обнаружения пика в данном случае аналогичен действию фильтра с выделением заданной частоты [11]. Традиционный фильтр, выделяющий полосу, основан на вычислении свертки исходного сигнала с синусоидальной функцией. В связи с ортогональностью и единственностью функций на основе производных четных порядков { S n ( t )}, в базисе этой системы может быть представлен сигнал исследуемого масс-спектра, аналогично представлению сигнала в традиционном гармоническом базисе. Выполнение операций свертки при n = 2 и n = 4 дает возможность выделить пик в заданной точке оси масс, если он там существует, точно так же, как свертка с синусоидальной функцией дает возможность выделить сигнал заданной частоты.

Затем по значению сверток в максимуме, используя формулы (11) и (12), можно вычислить полуширину ц и амплитуду А обнаруженного пика. Обозначим значение свертки у ₂( т ) в максимуме как С ₂, а значение свертки у ₄( т ) в максимуме как С 4 , тогда:

;

Г       А ц = ц • -2- -1

kC4    J

A =

Г

C 2 1

1 V

+ 7 2 цо у

2 пц

Предлагаемый метод проверен с помощью компьютерной программы.

Примеры работы метода

В табл. 2 представлены результаты исследования возможности алгоритма обнаруживать и оценивать параметры одиночного пика при различных отношениях сигнала к шуму. На рис. 7, 8

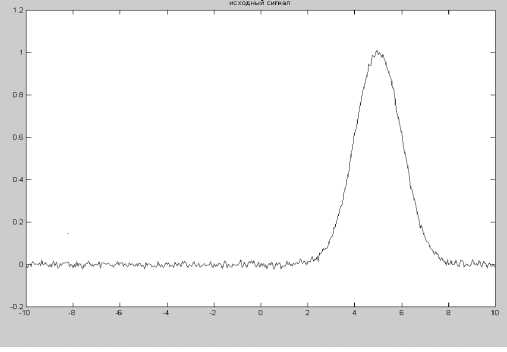
Рис. 7. Исходный сигнал с соотношением сигнал / шум 100

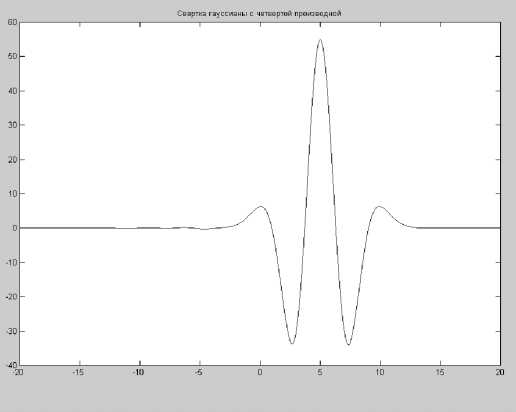
Рис. 8. Свертка сигнала (рис. 7) с четвертой производной гауссианы

Табл. 2. Возможности алгоритма обнаруживать и оценивать параметры одиночного пика при различных отношениях сигнал / шум (с/ш)

Отношение с/ш Значение амплитуды пика в мВ Погрешность оценки в % 100 1000 0 10 1004 0.4 5 1021 2 1 1070 7 0.5 1160 16 представлены графики, исходного гауссового сигнала с отношением сигнал / шум 100 и результат обнаружения центра пика с помощью свертки с четвертой производной.

На рис. 9, 10 представлены аналогичные графики для отношения сигнал / шум 0.5.

Гауссовы функции, с производными которых производятся свертки, должны иметь полуширину примерно в 1.5–2 раза меньше, чем полуширина пика в сигнале масс-спектрометра.

ЗАКЛЮЧЕНИЕ

Рассмотренные алгоритмы позволяют снизить погрешности измерений изотопных отношений в автоматизированных масс-спектрометрических комплексах различного назначения и работающих по разным методикам. Несмотря на разнообразие методик и задач масс-спектрометрического изотопного анализа они отражают единый подход к первичной обработке масс-спектрометрических измерений.

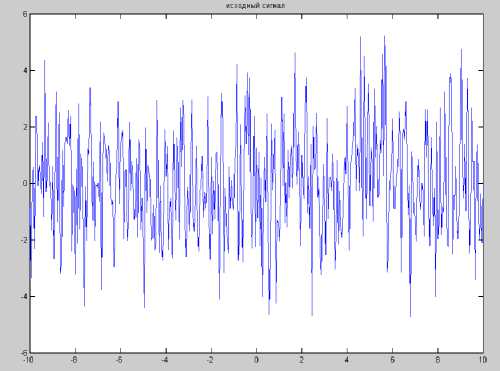
Рис. 9. Исходный сигнал с соотношением сигнал/шум 0.5

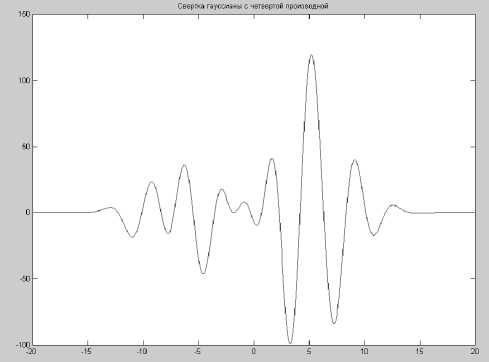
Рис. 9. Свертка сигнала (рис. 8) с четвертой производной