Относительные фазовые проницаемости в моделировании (на примере гидродинамических моделей)

Гидродинамическое моделирование процесса разработки – это эффективный инструмент, который позволяет определить основные моменты добычи нефти: структуру остаточных и извлекаемых запасов, определение потенциала разработки и многое другое. Это способствует развитию нефтедобывающей отрасли и просчета эффективности отдельных мест добычи в частности [1].

Для моделирования гидродинамических процессов крайне важны функции фазовых проницаемостей. Это данные, которые зависят от коэффициента насыщенности флюидами. С помощью этих функций и определяется точная модель двухфазного течения, которая по большей части представляет собой процесс вытеснения нефти водой.

Также стоит отметить, что текущее развитие нефтедобывающей отрасли в виде увеличения добычи нефти, а также введения сложных месторождений в разработку, сказывается на эффективности использования месторождений и более полной добыче нефти из недр. Для проведения подобных работ важно предельно точно понимать и описывать процессы, которые происходят в пластах, насыщенных флюидами. Именно гидромоделирование позволит создать связь между классическими и современными основами, которые представляют подземную гидродинамику.

Сегодня моделирование гидродинамических моделей является незаменимым элементом при создании проектов новых разработок. Для этого используются модели различных размерностей (2D, 3D), что позволяет получить важные данные о подземных процессах. Доступные сегодня программные комплексы позволяют прогнозировать показатели разработки, используя в основе интегрируемые системы нелинейных дифференциальных уравнений в частных производных. Для подобной математической модели необходимы крайне точные данные, касающиеся функций капиллярного давления и фазовых проницаемостей. Эти данные получаются экспериментально, производясь из расчетов на примере конкретных объектов.

Для определения функций ОФП наиболее часто используют экспериментальные исследования, берущие в основу проницаемости образцов керна. Подобные работы требуют соответствующую аппаратуру и занимают довольно много времени. Поэтому зачастую используют данные ближайших разработанных месторождений или для соответствующих пород. Это влечет за собой отклонения от настоящих показателей, ведь зависимости ОФП даже для одной породы могут отличаться на основе многих факторов. Поэтому для исследований ОФП в лабораторных условиях используются два главных метода: метод вытеснения и стационарной фильтрации. Первый метод основывается на нестационарных методах определения ОФП, где образец пористой среды, содержащий нефть и связную воду, накачивается водой. Это эффективный способ, который дает быстрый результат. При использовании второго метода берется тот же образец, в который закачивают некое соотношение воды и нефти. Каждый режим исследований дает свои показатели, представленные в виде результатов стационарной фильтрации. Но этот метод довольно долгий, а для его проведения требуется дорогостоящее оборудование. Но при использовании этих методов возникают некоторые сложности, связанные с описанием функции ОФП, а также с некорректной постановкой задач. Для решения этих проблем используются различные методы, включая использование данных от промысловых исследо- ваний скважин. Но результат использования ОФП, основанных на этих данных, может значительно отличаться от результатов лабораторных исследований. Также многие не учитывают, что в лабораторных исследованиях интерпретация данных производится с помощью определенной модели. Поэтому ОФП, которые были получены с помощью промысловых данных без использования соответствующих лабораторных результатов, нельзя принимать в качестве корректных. Причиной необходимости определения ОФП является то, что эти данные попросту незаменимы для создания рабочих моделей, ведь являются исходным материалов для определения показателей разработки. Поэтому результаты моделирования, которые предельно точно описывают процессы в пласте, позволяют добиться отличных результатов при проектировании, регулировании и анализе разработки различных месторождений, а также гидродинамических расчетах и прогнозе потенциала разработки. Это позволяет сказать, что математическая модель месторождения позволяет значительно повысить точность будущих прогнозов и произвести анализ различной важной информации, что является весьма актуальной задачей.

Что касается моделирования разработки месторождений, для этого активно применяются численные трёхмерные модели гидродинамики многофазной фильтрации. В их основе лежат геологические модели месторождений. Но иногда те содержат такое количество сегментов разностной сетки, что скорость вычисления становится крайне медленной. Так как это неприемлемо для исследовательских работ, необходимо уменьшить количество сегментов с помощью объединения нескольких мелких ячеек в крупные. Это позволит получить эквивалентные параметры крупных ячеек, основанных на параметрах от мелких ячеек, составляющих их. В итоге различие в скорости вычислений будет весьма существенно, что позволит привести этот показатель к приемлемой отметке [2].

Породы нефтяных месторождений состоят из двух или трех фаз. Во время фильтрации породы проницаемость для одной из нескольких фаз уступает ее абсолютной проницаемости. Зачастую именно фазовая проницаемость и отражает функцию насыщенности среды. Также на фильтрационные качества породы влияют следующие особенности: смачиваемость поверхности каналов фильтрующего материала, свойства жидкости и ее химические особенности на границах фаз, строение породы и другие параметры. Поэтому совместное фазное течение, состоящее с двух или трех фаз, изучается в экспериментальных лабораторных условиях, представляя процесс в виде зависимости фазовых проницаемостей от насыщенности водой. Во многофазных системах эффективность проницаемости для нефти и воды определяется следующим соотношением:

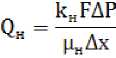
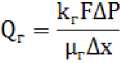
Экспериментальным путем было доказано, что фазовые проницаемости постоянно уступают абсолютным. Это касается и тех случаев, когда среда поддерживает лишь однофазную фильтрацию. Это подтверждается экспериментами с остаточной водонасыщен-ностью или нефтенасыщенностью породы, где фазовая проницаемость также была ниже абсолютной.

Для измерения ОФП используется несколько методов. Из них наиболее точным принято считать метод стационарной фильтрации. При его использовании в образец породы нагнетают смесь нефти и воды в определенном соотношении. Целью эксперимента является равенство составляющих на выходе. Процесс происходит при стабилизации перепада давления. Специалисты ОАО «ВНИИнефть» для расчета водонасыщенно-сти пористой среды предложили следующую формулу:

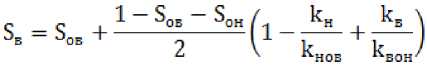
также удобнее будет выразить фазовые проницае- мости через составляющую долю воды:

с _ с I ^ ~ S°B ~ $он _ (1 ~ ^вАРнов) ^вАРвыЛ

В - ОБ       2             ^        др J

где fв и DP – это значение доли воды, содержащейся в жидкости, и общий перепад давления. Также водона- сыщенность среды можно вычислить с помощью электрического сопротивления, измеряя его для предварительно изученных образцов. Для использования этого метода породы должны иметь установленную зависимость параметра насыщения от коэффициента водона-сыщенности. Параметр насыщения – это отношение сопротивлений в частично водонасыщенной и полностью водонасыщенной породе. Важно отметить, что эксперимент возможен лишь при неизменной минерализации воды в процессе исследований.

В основе второго метода лежит анализ результатов для нестационарного эксперимента вытеснения нефти водой. Эксперимент происходит при постоянном перепаде давления или расходе. В его основе лежат расчеты соотношения закачанной воды и выкачанной нефти, а также замеры перепадов давления. После этого проводится обратное решение теории фильтрации, в котором функция обводненности определяется на основе изменения водонасыщенности в образце. И на основе обводненности происходит вычисление ОФП от водонасыщенности:

MS) / f(S) мkH(S) U-fts)*^/

После этого показатели функции насыщенности, отраженные в выходном сечении, определяются как:

, , /kB(S) kH(S)\y(S) = f^2 + ^2

' Pb Mu '

Также для определения ОФП применяется еще один способ, который регулярно используется в лабораторных исследованиях. Он имеет наименьшую точность, но позволяет получить результат на основе ка-пиллярометрии. При его проведении порода модели- руется в виде пучка капилляров, имеющих различный радиус, а результат фазовых проницаемостей опреде- ляется с помощью:

2 rS-sdS

^B_fs-idS ^S-0 P_K2

2 rS-1 dS

^H_fs-idS ^S-0 P₌2

где t выступает в качестве извилистости каналов фильтрации. Для расчета этого показателя используется формула Роуза-Уилли, представленная в виде: t ² = mР п ,

Здесь m отвечает за показатель пористости, а P _g – ее параметр. Однако сразу можно заметить множество допущений и небольших условностей, которые содержит последний метод. Это значительно снижает его точность, что и является причиной его низкой популярности. Экспериментальное сравнение показателей, а именно кривых фазовых от метода капилляров и метода нестационарного вытеснения показывает, что результаты имеют приблизительно одинаковую точность лишь в том случае, когда вязкость нефти не достигает 3-х мПа×с. Поэтому можно сказать, что метод можно использовать лишь для простых поровых пространств, которые содержат маловязкую и неактивную нефть.

Таким образом, методы исследования характеристики фильтрации на основе фазовых проницаемостей позволят значительно повысить понимание процессов вытеснения нефти жидкостями и способствовать исследованию пород в разработках.