Относительные характерные толщины динамического пространственного пограничного слоя при различных законах распределения скорости

Существующие на сегодняшний день логарифмические и степенные профили для аппроксимации эпюры скорости в пристеночном пограничном слое (рис. 1) имеют существенные недостатки [1] .

При логарифмическом законе распределения при у ^ 0; u ^ —да, что физически нереально, логарифмическая формула не может описывать распределение скоростей турбулентного потока в непосредственной близости от стенки, поскольку существует вязкий подслой, течение в котором характеризуется значительным влиянием сил вязкости и определяется почти линейным законом du         du распределения (т0 = ц— = const и    = const), подоб- dy          dy но ламинарному безнапорному течению (течению Куэтта).

Кроме того, — ^ 0 на толщине пограничного слоя (на dу оси трубы) как для степенного, так и для логарифмического профиля. Между тем, естественным условием на оси, подтверждаемым опытными данными, является I —        = 0 . Несмотря на эти недостатки профили ду у=5=R

(рис. 1) в основной части турбулентного ядра потока со- гласуются с опытными данными многих исследователей. Согласно Л. Прандтлю [2] установлен теоретический закон распределения скорости в поперечном сечении турбулентного потока в цилиндрической трубе, где y – расстояние от оси трубы либо от верхней границы пограничного слоя:

тт и ' 1 R и = U --ln-----, X R ^— У

где U – скорость на оси трубы; R – радиус трубы или толщина пограничного слоя 5 ; X — опытный числовой 0,5

I тп | коэффициент; U = I I - динамическая скорость;

U _с           ^ ^р ^

т ₀ = Хр — 8р- - напряжение трения; U _ср - средняя скорость.

Приближенно распределение скоростей при турбулентном течении предлагается оценивать вместо формулы (1) выражением

U — и

U

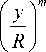
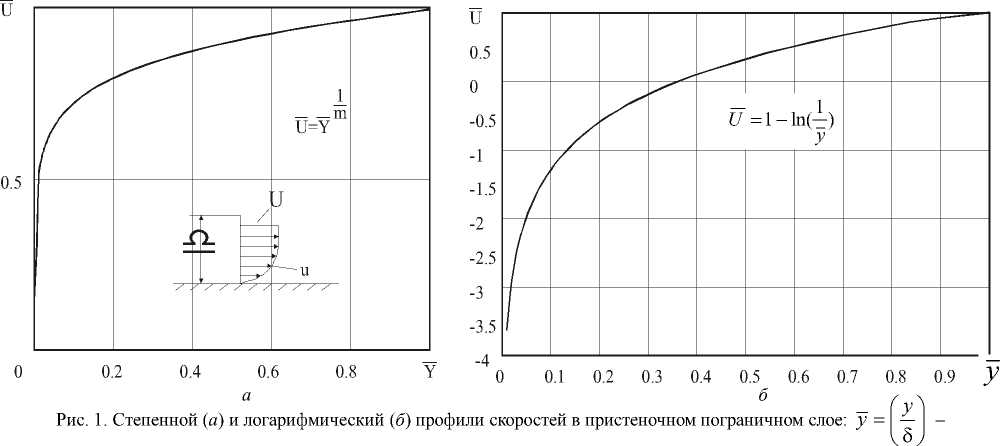
при у = 0 - точка на оси трубы и = U - согласуется с теоретическим значением (1). Примем более удобное для нашего случая обозначение y как расстояние от непод-

u относительная координата; о - толщина пограничного слоя; и =--относительная скорость

вижной стенки, тогда формула (2) преобразуется следующим образом:

U - u _! R - y I m

U

R

,

Толщина потери импульса продольного потока в поперечном направлении для степенного закона распределения профиля скорости (учтем, что профиль поперечной скорости выбираем по рекомендации) [3]:

y

или после преобразований с учетом u = U ; y = y

по-

лучим уравнение, выразив U :

u = 1 - (1 - У ) ^m -

тт U ,

W = U £— 1 U

^^^^^^в

\ 3^

U I

U ^j

;

5 **

ФУ

^^^^^^в

u I w I ₁ y I ^m = 1 -

U ^j U 0 1 5^j

Графически зависимость (4) представлена на рис- 2 совместно с выражением:

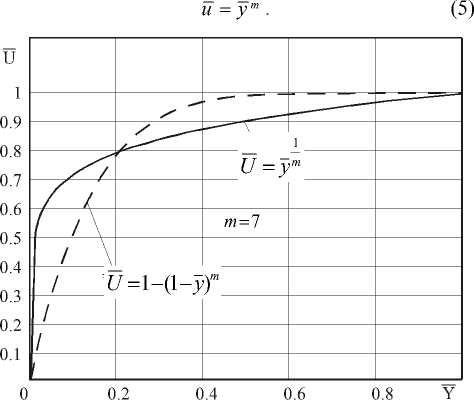
Рис. 2- Распределение профилей скоростей градиентного и степенного закона

I y I ^m

Х£

1.5 J

1 -I y I m

dy =

= £5 m

^^^^^^в  ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^в  ^^^^^^в

( m +1 m + 2 m + 4 m + 5 J

_          £5 m (6 m +18)

( m +1)( m + 2)( m + 3)( m + 4)( m + 5) ’ где £ - тангенс скоса данной линии тока-

Относительная характерная толщина ( J) для степенного закона распределения профиля скорости с учетом (11), (8) находится по выражению

j = 1 5

.**

I

ФУ

£ 5'

■ **

I

Ф

6( m + 3)

( m + 4) ( m + 5)

-

Толщина потери импульса поперечного потока в продольном направлении для степенного закона распределения профиля скорости:

3 _I

-dy = I U ^z

Следует отметить, что профиль (2) не имеет недостатков логарифмического (1) и степенного (5) профилей: в центре трубы ^ R = о и производную на неподвижной

=£?

у у y Im I y Im 5J +m

dy =

стенке:

^[1 - (1 - y ) ^m ] = m (1 - y ) ^{m - 1} d y^{L           J}

= £5 m

^^^^^^»

-

m + 2 m + 5

3 m

= £5

( m + 2)( m + 5)

-

Основные выражения для характерных толщин ППС степенного закона (5):

- толщина вытеснения

5Ф / X

Относительная характерная величина ( M) для степенного закона распределения профиля скорости с учетом (13), (8) имеет вид

м 15:

M =—

■ **

¹ УФ    ^{3( m +} 1)

5 ф

y =

£ 5'

¹Ф      ^{m + 5}

-

5 I

= 1 -

^^^^^^в

y i m

5 j

.         5        е..

dy =     =5 ;

m + 1

- толщина потери импульса продольного потока

u |, u I         I y I m

5, =     1 - dy =

^{Ф J} Ш Ui 15 j

х

^^^^^^в

У I ^m sj

dy =

m

( m +1 )( m + 2 )

5-

Относительная характерная толщина ( H) для степенного закона распределения профиля скорости рассчитывается по выражению

5 *

ф

- **

⁵ Ф

5    ( m + 1)( m + 2) = m + 2

( m + 1)      5 m

-

m

Толщина вытеснения поперечного потока рассчитывается по формуле

5       5      (

5 * = w =

^{У    J} o U ^J o

u

£ — 1

U

^^^^^^в

U I

U ^j

s 3 m

= £5---------------- (15)

( m + 1)( m + 4)

Обратим внимание, что 5 У*_Ф = 5 У -5 ф*_У [3], тогда с учетом (15) и (11) получаем выражение, тождественное (13):

е **      е*

5 =5

УФ У

-£5

^^^^^^в

_..    _      3 m

5.....= £5-------------

^ФУ ( m + 1)( m + 4) m (6 m + 18)

( m + 1)( m + 2)( m + 4)( m + 5)

£5 m

3 m ² + 15 m + 12

( m + 1)( m + 4) ^ ( m + 2)( m + 5)

3 m

= £5------------

( m + 2)( m + 5)

-

^^^^^^в

Толщина потери импульса поперечного потока степенного закона распределения профиля скорости имеет вид

5 * ^Ф

H =

5 ** ^Ф

5   ( m +1)(2 m +1)   2 m +1

( m +1)      5 m

m

-

2 (

о **

⁵ У

I dy =

Y2

0 V 7 к

( . Г . X 4 У и ( и I и "I и ^J .

dy =

£2=1

y I m

5 J

mm

21 y I +1 y I k5J k5J

dy =

= _£ 2 5 m I (1 — m )( m + 8) + ( m + 2)( m + 5) к     ( m + 2)( m + 5)( m + 8)

= £ ² 5

18 m

( m + 2)( m + 5)( m + 8)

= 5 **

У ^-

Относительная характерная толщина ( L ) для степенного закона распределения профиля скорости с учетом (16) и (8) равна

_L = X ^ =   18( m +1)

£² 5 ф *    ( m + 5)( m + 8)

-

Относительная характерная толщина ( F) связана с другими [3] и имеет вид

F = —

JM

-

Относительная (существенно положительная) характерная величина ( K) для степенного закона распределения профиля скорости находится по уравнению

**            **

к = M + J = ¹ -УФ + ¹ -ФУ- =

5 ф ^{£ 5} Ф

484 m ⁴ + 367 m ³ + 115 m ² + 17 m + 1

(3 m + 1)² (4 m + 1)(5 m + 1)

-

Рассмотрим аналогичные толщины ППС для закона профиля (4), и = 1 — (1 — y ) ^m , толщина вытеснения ( 5_ф ) выглядит следующим образом:

* .          I

0 ^k

m

dy -

y

—I

dy

Произведя замену переменных z = 1 — ; dz =--- ,

5        5

получим выражение

5* = — ^ф m + 1

-

Толщина потери импульса продольного потока составит

5           к 5 ( C

O** f ^U | 1 ^U | 7 fl | 1 5™ = — 1-- dy = 1 — 1 ^{ф J} Щ Ui     ¹   I

0 k V      0 к k

m y I

5 J

m

1 — y) dy

5J z-

Произведя аналогичную (19) замену переменных, получим формулу

**          ^{5 m}

5,. =------------------- ф (m +1)(2 m +1)

-

Относительная характерная толщина ( H ) для градиентного закона распределения профиля скорости имеет вид

Учтем, что профиль поперечной скорости [4] определяется выражением (10), толщина потери импульса продольного потока в поперечном направлении выглядит следующим образом:

**       r

ФУ       I

0 ^к

r х 1

к

и I w _ f U ^J U "j

m

^{1 —} y J,

1 —

m y I

£ X

5 J

1 —1 1 — y к 5

m k³

dy ,

сделав подстановку (19), после достаточно громоздких преобразований получим выражение

5 ** =£5

ФУ

2 m +1 3 m +1 4 m +1 5 m +1J’

или в другом виде

_**          £5 m (36 m ² + 11 m + 1)

5 =-------------------------- фу   (2 m +1)(2 m +1)(4 m +1)(5 m +1)

-

Относительная характерная толщина ( J ) для закона профиля (4) с учетом (20) и (22):

j = 1 5

**                             2

¹ фу = ( m + 1)(36 m + 11 m + 1)

£ 5^

i ф*    (3 m + 1)(4 m + 1)(5 m + 1)

-

Толщина потери импульса поперечного потока в продольном направлении для закона профиля (4) рассчитывается по выражению

г

=^£ J ^{1 —}I ¹

к

2 m

"sJ ,

,3

~ dy = I U ^z

m

1—Г1—y I к 5J

А5

dy -

Произведя замену переменных (19), после интегрирования имеем

5 **

УФ

, m + 1 2 m + 1 3 m + 1 4 m + 1 5 m + 1 J

или в другом виде

г **

⁵ УФ

2 £5 m ² (47 m ² + 12 m + 1)

( m + 1)(2 m + 1)(3 m + 1)(4 m + 1)(5 m + 1)

-   (24)

Относительная характерная величина ( M) для градиентного закона распределения профиля скорости с учетом (24) и (20):

15:

M =--

.**

I

УФ

£ 5

**

I Ф

£5 2 m ² (47 m ² + 12 m + 1)

£ ( m + 1)(2 m + 1)(3 m + 1)(4 m + 1)(5 m + 1) ( m + 1)(2 m + 1) = 2 m (47 m ² + 12 m + 1)

5 m

х

(3 m + 1)(3 m + 1)(5 m + 1)

-

Толщина вытеснения поперечного потока имеет вид

5     (

=4¹ —I ¹

0 ^к

—

m y I

5J

—

,3I

I dy =

m

1—Г1—y I к 5J

к4

dy ,

После замены переменных (19) и интегрирования получаем выражение:

5 *

V

+                           I , m +1 2 m +1 3 m +1 4 m +1J

или

5* =     s5 (26 m ³ + 9 m ² + m )

^V ( m + 1)(2 m + 1)(3 m + 1)(4 m + 1) ' Отметим, что проверка по выражению

**

L = -—- = 2 г»** ^{6 5} Ф

2 m ( m + 1)(7032 m ⁴ + + 2602 m ³ + 413 m ² + 32 m + 1) (3 m + 1)(4 m + 1)(5 m + 1) x

.

**      ~*

5 = 5

W V

5 ** = s5 (26 m ³ + 9 m ² + m )

^ФУ ( m + 1)(2 m + 1)(3 m + 1)(4 m + 1) e5 (36 m ³ + 11 m ² + m )      _

x (6 m + 1)(7 m + 1)(8 m + 1)

Относительная (существенно положительная) характерная величина ( K) для степенного закона распределения профиля скорости:

(2 m + 1)(3 m + 1)(4 m + 1)(5 m + 1)

=        2 e5 m ² (47 m ² +12 m + 1)

( m + 1)(2 m + 1)(3 m + 1)(4 m + 1)(5 m + 1)

дает результат, аналогичный уравнению (24).

Толщина потери импульса поперечного потока для закона профиля (4):

1 5**     1 5**

K = M + J =1 -Уф +1 -^у ф 6 5ф

5 Г

, 4 Y

I dy =

=6 ² J

Г

1 -1 1 - y

V 5

0 V m \²

Г

2 1

1 - y 5

m Л⁵

m

1 — y )

5 J

dy.

После замены переменных (19), интегрирования и достаточно громоздких преобразований получим выражение

Г 9

36     60

или

£** „2x ⁵ V = e ⁵

2 m + 1 3 m + 1 4 m + 1

54      28

,

5 m + 1 6 m + 1 7 m + 1 8 m + 1 J

о **

2 e ² 5 m ²(7032 m ⁴ + 2602 m ³ + + 413 m ² + 32 m + 1) (2 m + 1)(3 m + 1)(4 m + 1) x x (5 m + 1)(6 m + 1)(7 m + 1)(8 m + 1)

.

Относительная характерная толщина ( L ) для градиентного закона распределения профиля скорости с учетом (27) и (20):

m (3 m + 19) + 22

" ( m + 4)( m + 5) "

Очевидно, что использование градиентного закона распределения профиля скорости требует изменения всех относительных характерных толщин в уравнениях импульсов ППС и изменения закона трения, поскольку отношение толщин потери импульса степенного (5) и градиентного (4) закона распределения профиля скорости отличается от единицы:

2 m +1 _ ---------+1.

m + 2

Для степенного закона распределения профиля скорости m = 7 имеем согласно [3]:

т                Г и ₅ ** т^0,25

= 0,01256 —М   .       (30)

Р U          V v J

Для градиентного закона распределения профиля скорости m = 7 получаем с учетом (29):

_т              Г и ₅ ** Y^0,25

^0^ = 0,0111 —М   ,        (31)

Р U2         V v J где 5ф* для уравнения (30) вычисляется по (8); 5ф* для выражения (31) вычисляется по (20).

Для удобства относительные характерные толщины для законов (5) и (4) при различных значениях m сведены в таблицу.