Относительный метод передачи сигнала с одновременной коррекцией параметров среды распространения

Вопросы кодирования/декодирования сигналов и коррекция параметров среды распространения широко освещены в научной литературе. Данные операции выполняются раздельно и имеют ряд негативных явлений.

Одним из наиболее трудновыполнимых требований работы известных алгоритмов коррекции является необходимость наличия образцов сигнала передачи на приемной стороне.

В этой связи поиск алгоритмов кодирования/декодирования сигналов с одновременной коррекцией параметров канала связи является актуальной задачей.

Постановка задачи. Имеем информационный сигнал S(nT), содержащий N информационных отсчетов в каждом блоке. Между блоками передачи предусмотрен защитный интервал, содержащий N₂ нулевых отсчетов.

Будем полагать, что импульсная реакция эхо-тракта, содержащая N₂ информационных отсчетов и N нулевых отсчетов, также представлена отсчетами h(nT).

Требуется синтезировать алгоритм формирования сигналов на приеме с одновременной коррекцией межсимвольных искажений, вносимых каналом связи.

Решение задачи. Любой алгоритм обработки сигналов можно реализовать во временной и частотной областях обработки. Технические характеристики указанных выше алгоритмов идентичны.

Однако обработка сигналов в частотной области имеет преимущества перед обработкой во временной области. Эти преимущества заключаются в существенном уменьшении требуемых операций умножения.

В этой связи синтез указанного выше алгоритма произведем в частотной области обработки. На передаче сигнал во временной области представлен блоками 5 . (nT). С помощью ДПФ (или БПФ) произведем преобразование сигнала в частотную область [1]:

М - 1 - 2 ^ nk

S i ( jk ц ) = Х S i ( nT ) e^{N 1} , (1)

n = 0

где S(jkto) - энергетический спектр сигнала передачи на .-ом блоке; к - номер отсчета энергетического спектра; n - номер отсчета информационного сигнала; ц - кру- говая частота; N - количество информационных отсчетов в каждом блоке.

Используя рекуррентное соотношение, сформируем сигнал передачи следующим образом:

S вых ( ^jk ® 1 ) i = c i^S вых ( ^jk ® 1 ) i - 1 S i ( ^jk Ц ) ,       (2)

где с - коэффициент масштабирования; 5.(/кщД. - энергетический спектр сигнала передачи до преобразования (исходный сигнал); 5_в(/к ю ₁) . - энергетический спектр сигнала передачи после преобразования.

Коэффициент масштабирования, предусмотренный в каждом блоке формирования сигналов передачи, исключает явление переполнения разрядной сетки при реализации алгоритма в виде цифрового фильтра [2].

Сформированный таким образом сигнал передачи преобразуем во временную область с помощью ОБПФ:

N 1 ~ ¹                  j — nk

S _Bbix ( nT ) = - У S bb ix ( jk Ц ) e N ¹ .

ВЫХ          i                вых         1 / i

T k = 0

Дополним каждый блок 5 _вых ( пТ ) нулевыми отсчетами в количестве N, и через цифро-аналоговый преобразователь подадим его на вход канала связи (рис. 1).

Сигнал передачи, сформированный указанным выше способом, пройдя канал связи, преобразуется в соответствии со следующим соотношением [2]:

У (nT)i = Sвых (nT)i * h (nT)i =

N-1 (4) = y Sвых (kT)ih (kT - nT)i, k=0

где символ * обозначает операцию линейной или круговой свертки; h(nT) - отсчеты импульсной реакции канала связи; N^N₁ + N₂-количество отсчетов сигнала приема в каждом блоке; N₁ - количество информационных отсчетов сигнала передачи; N₂ - количество информационных отсчетов импульсной реакции.

Будем полагать, что на приемной стороне есть цикловой синхронизм. Поделим соседние блоки друг на друга, получим

Рис. 1. Структурная схема передающего устройства

S пр ⁽ jk « 1 ^ =

У i ( jk « 1 ) У i - 1 ( jk « 1 )

S вых ( jk « 1 ) H ( jk « 1 ) i

S вых ( jk « 1 ) i - 1 H ( jk « 1 L ,

гдеЯ"₁(/^ « ₁) - амплитудно-фазовый спектр канала связи.

Параметры любого канала связи на соседних блоках обработки можно считать неизменными [3], тогда выражение (5) преобразуется следующим образом:

S пр ⁽ jk « 1 ) =

= c . S i ( jk « 1 ) S вых ( jk « 1 ) i - 1 =

S _BB tx ( jk «1 ) , вых          1 1 —1

= cS ( jk « ) ,                 ⁽⁶⁾

С помощью ОБПФ преобразуем сигнал из частотной области во временную область и выдаем его потребителю (рис. 2).

Каждый демодулированный блок отличается от соответствующего блока на передаче постоянным множителем с . . Влияние этого коэффициента можно устранить дополнительным автоматическим регулятором усиления.

Оценим качественные характеристики данного метода:

• 1.    Влияние шумов квантования. В данном методе используется 2 аналого-цифровых преобразователя (АЦП), следовательно, мощность шумов квантования удваива

• 2.    Поведение разработанного метода при появлении перерывов связи. Пусть . блок обработки из-за перерыва связи потерян. Тогда 5_вых . (/^ « ₁) = А , где А - шаг квантования:

• 3.    В расчетах предполагается, что импульсная реакция h(nT) имеет N₂ информационных отсчетов и N₁ нулевых отсчетов. В действительности h(«T бесконечна. Усечение реальной характеристики до конечных размеров

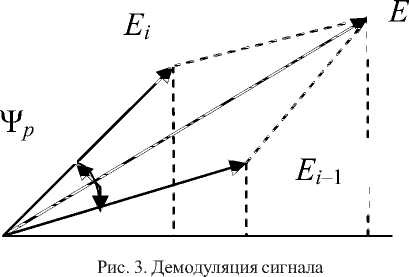
• 4.    Воздействие белого шума. Для расчета помехоустойчивости предлагаемого метода будем считать, что сигнал передачи (станция А) представляет собой относительный фазоманипулированный сигнал (ОФМ). Помехоустойчивость систем с ОФМ сигналами хорошо изучена, поэтому будет достаточно просто сравнить помехоустойчивость предлагаемого метода с классическими методами. Механизм демодуляции сигналов ОФМ по методу сравнения фаз приведен на рис. 3.

  

ется.

А yi(jk«)=ймsA I     (7)

У . + 1 ( jk « 1 ) = S ^{вых (} j « ¹ )'⁺ 1 ^ 2 r где r - разрядность обработки.

Пропадание одного блока приводит к неправильной демодуляции сигналов приема на 2-х блоках.

приводит к появлению дополнительных шумов.

Погрешность работы из-за этого явления будет равна

2 NT S ( nT ) h ( kT — nT ) £ S ( kT ) h ( kT — nT ) + £ [ S ( kT ) h ( kT — nT ) ] 2

= k =0 ______________________ k = N ________________________ k = N __________________________

N — 1

i S ( kT ) h ( kT — nT ) ]

,(8)

где S(nT - сигналы передачи; h(nT) - импульсная реак ция канала связи.

При больших выборках N данная погрешность будет несущественной.

Для расчета помехоустойчивости предлагаемого метода применительно к флуктуационной помехе найдем плотность распределения вероятностей результирующего значения Е на входе приемного устройства. Плотность распределения на выходе любого устройства можно рас считать, зная плотность распределения на входе данного устройства и оператор преобразования [4].

Зная Е., Е.+1, и Т^, с помощью элементарных преобра зований и рис. 3 получаем

^E i = E i ⁺ E ²+ 1 ^{+ 2} EE + 1^cos ( v p ^{+ па} . + 1 ) ,       (9)

где Е- принимаемый сигнал на i-ом тактовом интервале; Т ^ - разность фаз между .-м и (.+ 1)-м тактовыми интервалами принимаемого сигнала а . е {0,1}- передаваемый символ на входе передатчика. Плотность распределения на входе приемного устройства

W ( ^E i , v p ) = W ( E ) dE -+ dE _i

+ W ( E - + 1 ) dET + W ( v p ) d V p , dE _i          dE _i

где W(E . ) - одномерная плотность распределения величины Е . ; W( r _p) - одномерная плотность распределения разности фаз соседних векторов.

Многомерная плотность распределения для двухканальной фазовой системы определяется выражением [5]

Рис. 2. Структурная схема приемного устройства

W ( E iN , E 2 N , ψ p ) = ^{E iN E ( i + 1)} ₂ ^N exp × 2 π ( 1 - p )

ξ                                              ( 1 - p ² ) ²

- u ³ ⎡ 1 + 2 α cos ( ψ-ψ-µ ) +α ² ⎤

_{64 ⎣} ( p 0     ) _⎦ 3

⎡_⎣ 1 - p cos ( ψ _p -γ ) ⎤_⎦ ²

1 - p

×   ^{E ∑}    ,

E ₀ ² sin ψ _p

× exp ⎨

E_i ² _N - 2 pE_iNE _{( i + 1 ) N} cos( ψ _p -γ ) + E ₍ ² _{i + 1 ) N}

1 - p

^Х ,(11)

где Д =

1 - p ²

q ² - 2 pq ₁ q ₂cos ∆ϕ ₀ + p ² q ₁.

× I 0

1 - p ²

cos ∆ϕ ₀ + p ² q ₂ ×

× E i ² N + 2 α E iN E _{( i + 1 ) N} cos ( ψ p -ϕ-µ ) +α ² E ₍ ² _{i + 1 ) N} } ,

где

2 q ₂ - 2 pq ₁ q ₂cos ∆ϕ+ p ² q ₁

q ₁ - 2 pq ₁ q ₂cos ∆ϕ+ p ² q ₁

µ = arctg ×

Тогда общая вероятность ошибочного приема (для независимых событий) будет π

Р ош = Z Р (ai)Р (Г ) = 2 J i =1                          0

E nop

J W ( E ^ , V p ) dE ^ d V p .         (14)

Учитывая, что q₁ - q₂ -g, Е_пор - 1,41E₀, E²₀ 10 ' ^q [6], а также то, что помеха некоррелирована (р-0, р -0, а -1, t - 2q, и - ^ 2q, Д - ^ 2q), окончательно получим

×⎨ p sin ∆ϕ

q ₁ - 2 pq ₁ q ₂ cos ∆ϕ+ q ₂

q ₁ q ₂ ( 1 + p ² cos2 ∆ϕ ₀ ) - p ( q ₁ + q ₂ ) cos ∆ϕ ₀

ош

= 2exp ^⎧ - ^⎛ 2 q + 110^{0,1 q} _⎩⎜_{⎝ 4}

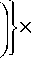
Е- нормированная величинаЕ , на z-ом тактовом интер

× ( 1 - 2 q 10^{0,1 q} ) ( 1 - q ) 10^{0,1 q} .

вале; q₁, q₂ - отношение мощности сигнала к мощности

помехи соответственно для первого и второго каналов; р - обобщенный коэффициент корреляции двухканальной помехи; у- обобщенный фазовый параметр двухканальной помехи; Д^ ₀ - % - Y - разность фазовой расстройки сигнала и двухканальной помехи; 1₀(х) - модифицированная функция Бесселя нулевого порядка.

Воспользовавшись разложением функции Бесселя в ряд [6] 1₀(х) = 1 -х²/2 и введя для краткости обозначения

t=

q ₁ - 2 pq ₁ q ₂cos ∆ϕ+ q ₂

1 - p ²

u=

1 - p ²

q ₁ - 2 pq ₁ q ₂cos ∆ϕ+ p ² q ₂

формула (11) перепишется в виде

_{W ( E iN , E 2 N , ψ p )=} ^EiN^E ( i + 1) N _× 2 π ( 1 - p ² )

× e ^{- t} exp

E _i ² _N - 2 pE _iN E _{( i + 1 ) N} cos( ψ _p - γ ) + E ₍ ² _{i + 1 ) N} 4 ( 1 - p ² )

u ² ⎡_⎣ E _i ² _N + 2 α E _iN E _{( i + 1 ) N} cos( ψ _p -ϕ-µ ) +α ² E ₍ ² _{i + 1 ) N} ⎤_⎦

,(12)

Воспользовавшись формулами (9), (10), (12), получим окончательную формулу для плотности распределения W(E_y, Т _р) на входе приемного устройства:

W ( E _∑ ,

E ψ p ) = _{1 -} ⁰ _p 2 ⋅ e ^{- t} exp

4 ( 1 - p ² )

( 1 - u ² E 0² ) ×

Графики помехоустойчивости для абсолютной фазовой манипуляции (1) классической ОФМ (2), предлагаемого метода передачи (3), из которых видно, что помехоустойчивость предлагаемого метода практически совпадает с помехоустойчивостью классической ОФМ представлены на рис. 4. Все приведенные выкладки касались фазовой манипуляции, но они справедливы и для биим-пульсного сигнала, который является предельным случаем фазовой манипуляции; поэтому предлагаемый метод может найти широкое применение в высокоскоростных системах связи, работающих по кабелям связи с использованием биимпульсных сигналов.

0 4   5    6   7    8    9    10 q, дБ

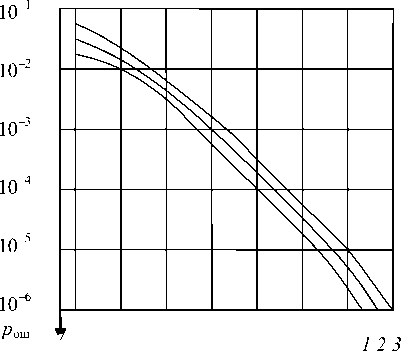
Рис. 4. Кривые помехоустойчивости

11 ⎛ p ²   2 ⎞ p ² ∆ ² E 0²

-        +∆+

2 ( 1 - p ² ) 4 ( 1 - p ² ) ^{2 ⎜} ⎝ ^{1 - p 2 ⎟}⎠ ( 1 - p ² ) ⁴

2 E _∑             e - t π   ⎧_⎪ 1         1 _- p 2

-

E ₀ ⎡_⎣ 1 + cos ψ _p ⎤_⎦ 2 π ( 1 - p ² ) ⎪_⎩ 4 1 - p cos ( ψ _p -γ )

Следует заметить, что кривые 1 и 2, отражающие помехоустойчивость абсолютной ФМ и ОФМ, рассчитаны без учета искажений среды распространения.

Таким образом, предлагаемый метод может найти широкое применение в системах телекоммуникаций.