Отображение областей, ограниченных прямолинейными многоугольниками

Для доказательства теоремы 1 сформулируем вспомогательный материал.

Теорема 2 (Римана). Для любых V_o и V единственным образом определено отображение р = g (z) , переводящее область V₀ на область V₁, причем g(z o ) = ( о , arg g(z 0 ) = а о , где z o Е V , ( о Е V , а о Е IR.

Теорема 3 (Римана—Шварца) (принцип симметрии). Пусть D1 и D1 — области, имеющие жордановы границы dD1 и dD1, причем dD1 содержит часть прямой или дугу окружности у, а dD*— такую же часть или дугу у*. Тогда если функция f1 реализует конформное отображение D1, на D*, при котором f1(y) = у*, то f1 допускает аналитическое продолжение в симметричную с D1 относительно у область D2, и продолженная таким образом функция отображает область D1 U у U D2 на D1 U у U D2 конформно, если D1 П D 2 = 0 и D* П D2 = 0.

3амечание 2. В случае, если промежуток у * содержит бесконечную точку, продолжение

/ будет мероморфным. То есть функция / окажется голоморфной в D всюду, кроме точки z₀ G у, соответствующей бесконечной точке, где она имеет полюс обязательно первого порядка, так как / однолистна в области D (вблизи кратного полюса функция многолистна).

Доказательство теоремы 1. По теореме Римана существует функция р = g(z"), конформно отображающая плоскость z + на ограниченный многоугольник Р_п , причем т ^ ^ го, i = 1,2, ..., п. Такая функция имеет ряд свойств.

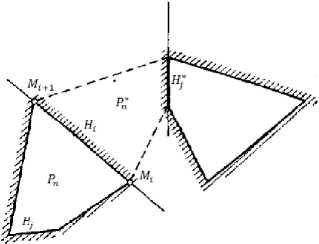
Пусть G(z^ — аналитическая функция с исходным элементом g(z) /т z > 0. Покажем, что функция G(z) является аналитической во всей расширенной комплексной плоскости с выколотыми точками т^, i = 1, п. Функция р = g(z) переводит интервал h [ = (т [ ,т [ ₊₁) в интервал Щ = (М [ , М ^ ₊₁). Исходя из принципа симметрии, заключаем, что через отрезок (т ^ ,т ^ ₊₁) существует аналитическое продолжение g*(z~) функции g(z~) в нижнюю полуплоскость /т z < 0. Функция р = g(z') конформно отображает полуплоскость /т z < 0 на многоугольник Р П* , симметричный относительно грани М [ М [ ₊₁ с областью Р_п . При таком отображении интервал H j* , симметричный H j относительно грани M_tM_t+1 , является образом интервала h j .

Предположим, что выполнены все возможные аналитические продолжения. В результате получится бесконечнозначная аналитическая во всей расширенной комплексной плоскости функция р = G (z) с выколотыми точками т ^ , i = 1,п.

Теперь докажем, что функция /(z)

g"(z)

= ^7^ однозначна и регулярна во

всей расширенной комплексной плоскости с выколотыми точками m i (I = 1^.

Пусть р = g*(z') и р = g**(z) — две произвольные ветви функции G(z') в плоскости z+. Тогда, из вышеизложенного, эти ветви отображают верхнюю полуплоскость конформно на два многоугольника Р^ и Р* соответственно. Учитывая, что любая пара симметрий относительно двух произвольных прямых сводится к некоторому сдвигу и повороту, запишем функцию g**(z') в виде g**(z) = eiag*(z") + а, где z G z+, а, а —константы. Это справедливо и для ветвей в нижней полуплоскости. "

Функция /(z) = -^т^ = — Ing'(z) аналитична в плоскости z+ в силу того, что g'(z~) ^ 0 при любом z как производная функции конформного отображения. Функция f(z~) будет однозначной при всевозможных аналитических продолжениях g(z) Следовательно, f (z') однозначна во всей расширенной комплексной плоскости с выколотыми точками mi (i = 1,n). Регулярность /(z-) в бесконечности следует из того, что z = т переходит не в вершину многоугольника, а в некоторую точку на его стороне.

Определим вид функции /(z^-) в точке z = m i :

f⁽z) = ( i + ⁽z — m i ^{)a i (}a₀ + a 1 ⁽z — m i ) + •••).

Тогда разложение Лорана функции /(z-) вблизи точки z = mi будет иметь вид:

/(z) =

g"(z) _ (a i -1)a o a i (z-m i ) ^ai ² +-.

g ' (z)       a o a i (z-m i ) ^ai^-1 +-

—---+ a' + a'(z — m^) + ■■■,

z-m t     0    ¹

откуда видно, что точка z = mi для функции /(z) является простым полюсом с вычетом а — 1. Следовательно, /(z') во всей плоскости имеет только n особых точек.

Определим функцию F(z^ как разность функции f(z) и главных частей ее разложения в особых точках:

d 1 -1     (Х 2 — 1           (Z_n — 1

----...--. z—m 1   z—m₂       z—m_n

Полученная функция является регулярной на всей плоскости z. Так как в точке z = от функция f(z) правильна, то в ее окрестности

g(z)   do + dp. , 1L--, ....

f(z) =

d—p .

P ⁽ P ^{+ 1)} ZP+2 +^ _

pd—p zP⁺¹⁺" "

P+1   d —2

— .  +  . +-■ •

При z = от получим f (от) = 0, следовательно, F(ot) = 0. Тогда

[(/) ^Ing'U) — + — L4 —.

dz          z—m 1   z—m₂       z—m_n

Проинтегрировав полученное выражение вдоль любого пути, лежащего в области Im z > 0, а затем потенцируя его, получим

g'(z) = C(z — m1)d1—1(z — m2)a2—1... (z — mn)dn—1.

Интегрируя последнее выражение, получим представление для g (z)

g(z) = C fz (z — m1)ai—1(z — m2)a2—1... (z — mn)“n—1 dz + C1.

^Z 0

Теорема доказана.

• 2)    Одна из вершин многоугольника – образ бесконечно удаленной точки.

Пусть m_n = от. Введем линейное преобразование е = —¹ + m ^ плоскости z⁺ на верхнюю полуплоскость е, при котором точки m 1 , m 2 , ..., m_n перейдут в конечные точки m ‘ , m₂, .., m^. Тогда по теореме Шварца - Кристоффеля получим:

g(z) = C f£ (е — m1)ai—1(E — m2)a2—1... (е — mL)dn—1 de + C1= £0

=^C i Z"; 2 ^(m" ^{— m} 1 ^{— 1}) “ ^{1 -(m}n ^{— m}г-^^{)a 2} * .(^— | ^)d ” ^{1dz + C} 1 =

= C/ZZ

^Z 0

(z—m₁) “^{1 1} (z—m₂) ^a2 1 .(z—m_n-1 ) “^{n-1 1}

zC^1+t^2+^+t^'n —71 + 2

dz + C 1 ,

где т^ =      — некоторые вещественные константы, а С — комплексная постоянная. С учетом формулы суммы углов п —угольника, по которой а1 + а2 + —+ ап = п — 2, окончательно имеем

Ф = С (^z (z — т_г)^а 1 ¹^ — т₂)^а 2 ¹ ... (z — т_л_₁ )^а ^-1 ¹ dz + С_г.

zo                                               п

Из последнего выражения видно, что если одна из вершин многоугольника – образ бесконечно удаленной точки, то множитель, относящийся к этой вершине, в формуле Шварца – Кристоффеля отсутствует.

• 3)    В бесконечно удаленной точке лежат одна или больше вершин многоугольника.

Допустим, такой вершиной является М [ . На лучах M_tM_t+1 и М_1-1М₁ отметим произвольным образом точки М [ и М ' . Соединяя эти точки, получим (п + 1) —угольник Р_л. Функция, отображающая полуплоскость на многоугольник Р П выражается формулой

‘                                ‘‘

Ф = С/ (z — т₁)^{a 1 1}„(z — т^)^a ^ ¹(z — т^ )^{а 1}

^Z 0

... (z — т_п )^а ” ¹ dz + С 1 ,

где а ' и а ' — углы при вершинах М - и М ' , измеренные в долях п, а т ' и т '' — точки действительной оси, соответствующие этим вершинам.

Пусть отрезок М [ М ' с помощью параллельного переноса удаляется в бесконечность так, что точки т ' и т '' сливаются в одну т ^ , соответствующую вершине М ^ . Обозначим через а ^ п угол пересечения лучей М_1-1М [ и М [ М₁₊₁ в конечной точке М * , взятый со знаком минус. Из треугольника М '^ М '^ М * имеем а ' + а ' — а = 1, т.е. а ’ + а " — 2 = а ^ — 1. Тогда формула (1) примет вид

Ф = С f^Z (z — т 1 )^{а 1 -1} „.(z — т ; )^{а -1} „.(z — т_п )^а ^ ^-1 dz + С 1 .

^Z 0

В случае, когда в бесконечности лежат несколько вершин многоугольника, рассуждение проводится аналогично.