Отработка методов проведения экспериментов в области микрогравитации в автономном полете грузового корабля «Прогресс М-20М»

беляев м.ю .

ЛЕГОСТАЕВ В.П.

МАТВЕЕВА Т.В.

МОНАХОВ М.И.

РУЛЕВ Д.Н.

сазонов в.в .

МОНАХОВ Михаил Иванович — ктн, начальник сектора РКК «Энергия»,

Режимы вращательного движения ТГК «Прогресс» для проведения экспериментов в области микрогравитации

Начиная с 1978 г., транспортные грузовые корабли (ТГК) «Прогресс» успешно работают по программам долговременных орбитальных станций. После выполнения своих основных задач ТГК нередко обладают ресурсами основных систем, позволяющими им совершать автономный полет в течение нескольких месяцев. Целесообразно использовать возможности такого полета для проведения различных исследований [1], в частности, экспериментов в области микрогравитации.

Остаточные микроускорения на Российском сегменте Международной космической станции (МКС) слишком велики для исследования некоторых гравитационно-чувствительных процессов. В связи с этим изучается возможность проведения экспериментов с ними на ТГК «Прогресс» во время автономного неуправляемого полета. Неуправляемый полет необходим для обеспечения малого уровня остаточных микроускорений на борту, причем, чтобы минимизировать этот уровень, режим вращательного движения ТГК должен быть выбран специальным образом. В некоторых экспериментах режим неуправляемого вращательного движения должен обеспечивать заданные уровень микроускорений и характер их изменения во времени. В ходе соответствующих летных испытаний [2–4] производился выбор устойчивых режимов вращательного движения, обеспечивающих в течение нескольких суток как минимальный, так и требуемый для экспериментов уровень остаточных микроускорений. Эксперименты по поиску режимов, обеспечивающих малый уровень микроускорений, проводились на ТГК «Прогресс М1-11» (май–июнь 2004 г.), «Прогресс-51» (февраль–март 2005 г.) и «Прогресс М-20» (февраль 2014 г.). Поиск режимов, обеспечивающих заданные уровень микроускорений и характер их изменения во времени, проводился на перечисленных кораблях, а также на ТГК «Прогресс М-11М», «Прогресс М-13М», «Прогресс М-14М», «Прогресс М-15М» и «Прогресс М-17М». Один из найденных вариантов — режим закрутки на Солнце, опробованный в шести последних по времени полетах [3, 4], предназначен для экспериментов с датчиком конвекции «Дакон».

Минимальный уровень микроускорений обеспечивается при гравитационной ориентации ТГК. В этом режиме продольная ось корабля совершает малые колебания относительно местной вертикали, нормаль к плоскости солнечных батарей составляет малый угол с нормалью к плоскости орбиты. Однако, во-первых, этот режим сохраняется сравнительно недолго вследствие дестабилизирующего действия на корабль аэродинамического момента и ошибок в задании начальных условий. Во-вторых, приемлемый энергосъем с солнечных батарей обеспечивается в этом режиме только в том случае, когда Солнце находится достаточно высоко над плоскостью орбиты.

Устойчивая одноосная гравитационная ориентация и необходимый приход электроэнергии от Солнца могут быть обеспечены выполнением закрутки ТГК вокруг продольной оси в определенный момент времени и с определенной скоростью [5, 6].

При этом средневитковый энергосъем даже в наихудшем случае, когда Солнце лежит в плоскости орбиты корабля, составляет не менее 10% от максимально возможного (реализуется при непрерывном освещении батарей и нулевом угле падения солнечных лучей на их плоскость). Максимальный средневит-ковый энергосъем в этом режиме — 32% — реализуется на орбите, плоскость которой ортогональна направлению «Земля – Солнце». Однако даже на орбитах с наклонением 51,6 ° средневитковый энергосъем может быть повышен при надлежащем фазировании вращения корабля вокруг продольной оси с его орбитальным движением [5, 6].

Ниже описываются результаты использования этого режима на корабле «Прогресс М-20М» 7–9 марта 2014 г., которые существенно полнее результатов [2], поскольку основаны на более полной телеметрической информации. В работе [2] для определения движения кораблей использовались только значения тока, снимаемого с солнечных батарей (СБ). В новых экспериментах были дополнительно получены еще и измерения угловой скорости корабля, гораздо более информативные, чем измерения тока. Кроме того, измерения тока, согласно [3], содержат не только легко учитываемый вклад от прямого солнечного излучения, но и вклад от излучения, отраженного поверхностью Земли. Специфика режима гравитационной ориентации вращающегося спутника такова, что измерений угловой скорости достаточно для определения движения корабля в этом режиме. Именно так было выполнено определение вращательного движения МКС [7].

Ниже приводится описание методики обработки собранной телеметрической информации и результаты определения с ее помощью фактического вращательного движения корабля.

Математическая модель вращательного движения корабля

Корабль считается твердым телом. Для записи уравнений движения корабля относительно центра масс и соотношений, используемых при обработке данных измерений, вводятся три правые декартовы системы координат.

Строительная система Oy ₁ y ₂ y ₃ жестко связана с корпусом корабля. Точка O — центр масс корабля, ось Oy ₁ параллельна его продольной оси и направлена от стыковочного узла к агрегатному отсеку, ось Oy ₂ перпендикулярна плоскости СБ. В этой системе интерпретируются данные измерений угловой скорости. Светочувствительная сторона СБ обращена к полупространству у 2 > 0. Полагаем, что оси строительной системы являются главными центральными осями инерции корабля. Обработка по методике [3] измерений угловой скорости корабля «Прогресс М-20М», выполненных в режиме закруток на Солнце в марте 2014 г., показала, что отклонение главной центральной оси минимального момента инерции от оси Оу 1 составляет менее 1 ° , отклонения осей максимального и среднего моментов инерции соответственно от осей Oy ₂ и Oy ₃ не превосходят 5 ° .

Система CY ₁ Y ₂ Y ₃ близка ко второй геоэк-ваториальной системе координат эпохи даты. Ее начало находится в центре масс Земли, плоскость CY ₁ Y ₂ совпадает с плоскостью экватора, ось CY ₃ направлена в северный полюс мира, ось CY ₁ направлена приблизительно в точку весеннего равноденствия — повернута от плоскости Гринвичского меридиана на среднее звездное время против вращения Земли. В системе CY ₁ Y ₂ Y ₃ задаются двухстрочные элементы NORAD , которые использованы для задания орбитального движения корабля. Эту систему считаем инерциальной.

В орбитальной системе координат OX1X2X3 оси OX3 и OX2 направлены соответственно по геоцентрическому радиусу-вектору центра масс корабля и по вектору его орбитального кинетического момента. Положение системы Oy1y2y3 относительно системы OX1X2X3 будем задавать углами у, 8 и в, которые введем посредством следующего условия. Система OX1X2X3 может быть переведена в систему Oy1y2y3 тремя последовательными поворотами:

• 1)    на угол 8 + п /2 вокруг оси OX ₂;

• 2)    на угол в вокруг новой оси OX 3 ;

• 3)    на угол у вокруг новой оси OX 1 , совпадающей с осью Оу 1 . Углы 8 и в задают направление оси Oy ₁ в орбитальной системе координат, угол у задает поворот корабля вокруг этой оси.

Матрицу перехода от системы Oy ₁ y ₂ y ₃ к системе CY ₁ Y ₂ Y 3 обозначим lib || 1 . Здесь b — косинус угла между осями CY_i и Oy_j . Элементы этой матрицы параметризуем углами у b , 8 b и в b , которые вводятся аналогично углам у , 8 и в.

Уравнения вращательного движения корабля образованы динамическими уравнениями Эйлера для компонент его угловой скорости юi (i = 1, 2, 3) в системе Оу 1 у2у3 и кинематическими уравнениями Пуассона для первой и второй строк матрицы ||b^.||. В уравнениях Эйлера учитываются действующие на корабль гравитационный и восстанавливающий аэродинамический моменты, а также постоянный момент вдоль оси Oy1. Уравнения движения имеют вид y y                + ε

. ц' - ц                к(1-ц')

y y y y

к(1 - Ц') z

^1Р‘

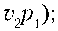
'11 1	t>l2O)3 -.			о„со3 — 1	Ь,3со9;
12 = '	^13®1 - '	ЬцСОз;	622 =	ьй«\ -	621юз;	(1)
'13 ~ '	b ।!со, — .	^12Ю1’	^23 ” ‘	ЬЧ1®2 -	^СОр

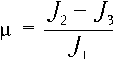
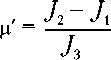
Зце

1F’ y y y

к = Ер_а\ v^ + у² + у₃² ,

где точка над символом означает дифференцирование по времени t; yi и vi — компоненты в системе Oy1y2y3 геоцентрического радиуса- вектора точки O и скорости этой точки относительно поверхности Земли; pi — параметры аэродинамического момента; е — угловое ускорение, создаваемое постоянным моментом; Ji — моменты инерции корабля относительно осей Oyi; цe — гравитационный параметр Земли; рa — плотность атмосферы в точке O (рассчитывается согласно модели

ГОСТ Р 25645.166-2004); E — масштабирующий множитель.

При численном интегрировании уравнений (1) единицами измерения времени и длины служат 1 000 с и 1 000 км, единицы измерения других величин: [v. ] = км/с; [mi] = 10-3c-1; [p.] = см/кг; [рa] = кг/м3; E = 1010. Третья строка матрицы ||b„|| вычисляется как векторное произведение ее первой и второй строк, начальные значения переменных b1i и b2i выражаются через углы yb, 8b и вb. Тем самым обеспечивается нужная точность выполнения условий ортогональности этой матрицы. Величины yi и vi задаются формулами з y к кг'

у. = Hv.b,. (г = 1, 2 , 3), , где                                            .

Здесь ю e — угловая скорость вращения Земли, координаты Y_k и компоненты скорости точки O в системе CY ₁ Y ₂ Y ₃ вычисляются в функции времени с помощью модели SGP 4 [11] по подходящему набору двухстрочных элементов.

Параметры ц , ц' в уравнениях (1) были найдены в результате обработки по методике [3] измерений угловой скорости корабля «Прогресс М-20М», выполненных в режиме закруток на Солнце в марте 2014 г. Их значения ц = 0,159; ц' = 0,871 . Параметры е и p i определяются из обработки данных измерений наряду с неизвестными начальными условиями движения корабля, т. е. служат параметрами согласования.

Режим гравитационной ориентации вращающегося спутника

Чтобы пояснить этот режим, рассмотрим уравнения (1) в упрощенной ситуации, которая в случае кораблей «Прогресс» близка к реальности. Примем, что орбита корабля круговая и неизменна в системе координат CY1Y2Y3. Матрицу перехода от орбитальной системы к системе CY1 Y2Y3 обозначим || ci. ||. ,_t, где ci. — косинус угла между осями CYi и OXj. Элементы этой матрицы будем выражать через наклонение орбиты, долготу ее восходящего узла и аргумент широты точки O. В рассматриваемом случае наклонение и долгота восходящего узла постоянны, аргумент широты линейно зависит от времени. Скорость изменения аргумента широты (среднее движение) 0    e/R3 , где R — радиус орбиты корабля. Движение точки O по орбите описывается соотношениями Yi = Rci3 (i = 1, 2, 3) . Матрицу перехода от системы Oy1y2y3 к орбитальной системе обозначим 11 а..\ | .    , где aij — косинус угла между осями OXij и Oyj. Элементы aij выражаются через введенные выше углы y, 8 и в [2]. Введенные матрицы позволяют получить соотношения yi = Ra3i, где а31 = - cos 8 cos в;

а ₃₂ = — sin 8 sin Y + cos 8 sin в cos Y ;

a33 = - sin 8 cos y - cos 8 sin в cos Y, а также вывести соотношения у = (Bj- tg 3(co.,cos у - ®3 sin y);

δ _cos β    ₂cos γ – ω ₃sin γ ) – ω ₀;     (2)

β = ω ₂cos γ – ω ₃sin γ .

Предположим далее, что корабль имеет два равных момента инерции J ₂ = J ₃, и к нему приложен только один внешний механический момент — гравитационный. Это значит, в системе (1) следует положить ц = 0; е = 0; p ₁ = p ₂ = p ₃ = 0. В результате первые три уравнения этой системы можно записать в виде

₂     (    ₃ – 3 ²₀ a ₃₁ a ₃₃);           (3)

₃ – ( ₂ – 3 ₀² a ₃₁ a ₃₂).

Уравнения (2, 3) образуют замкнутую систему, описывающую вращательное движение корабля относительно орбитальной системы координат. Эта система допускает два семейства частных решений, в которых ю1 = О;

ю₂ = ю₀ cos в cos y;

ю₃ = - ю₀ cos в sin y;

4 Ω t

γ _{+ 3} + γ ₀;                ₍₄₎

sin δ = 0;

(1 – ) Ω β = arcsin              ,

( + 3 ) ω ₀

где y₀ и О — произвольные постоянные; (1 - ц' ) I О | С (1 + 3 ц' ) ю₀ . Одно семейство получается при 8 = 0, другое при 8 = п . При 0 <  ц' < 1 решения (4) устойчивы по переменным 8 , в , 8 и в [8]. При 0 < 1 - ц' << 1 эти решения можно использовать для реализации режима гравитационной ориентации вращающегося спутника. Например, при ц' = 0,87 и О = 0,2 ° /с имеем в (4) в = 6,2 ° , т. е. ось Оу 1 мало отклоняется от оси ОХ ₃ при 8 = п или оси (- ОХ ₃) при 8 = 0.

У кораблей «Прогресс» эксцентриситет орбиты и параметры ц , е , p_i — малые величины.

По этой причине уравнения (1) допускают решения, которые, если их выразить через углы γ , δ и β , оказываются близкими решениям (4). Движения, описываемые такими решениями, были реализованы в экспериментах с кораблем «Прогресс М-20М». Результаты определения этих движений описаны ниже.

Методика обработки данных измерений

В экспериментах с вращательным движением корабля измерялись компоненты угловой скорости ω _i ( i = 1, 2, 3) и электрический ток, вырабатываемый СБ. Данные измерений по телеметрическому каналу передавались на Землю. Обработка этих данных, относящихся к одной и той же реализации режима, состояла в поиске решения уравнений (1), наилучшим образом согласующего эти данные с их расчетными аналогами.

Данные измерений угловой скорости имеют вид tn, ω ω ω , (n = 1, 2,  , N),       (5)

где _i ( i = 1, 2, 3) — приближенные значения компонент угловой скорости ω _i в момент времени t_n : _i ≈ ω _i ( t_n ), t ₁ < t ₂ < ... <  t_N . Разности t_{n +1} – t_n принимают значения от нескольких секунд до нескольких десятков секунд в зависимости от способа сбора телеметрической информации.

Данные измерений тока СБ представляют собой три ряда значений, получаемых от трех датчиков:

( m = 1, 2, ..., M ),       (6)

где — приближенное значение тока, фиксируемое в момент времени датчиком с номером j (j = 1, 2, 3);               . Если не принимать во внимание дублирующие данные, то t^— - t= = 1 с. Расчетный аналог тока СБ имеет вид где I0 — максимально возможный ток СБ; η — косинус угла между осью Oy2 и ортом направления «Земля – Солнце», имеющим в системе CY1Y2Y3 компоненты Sk. Зависимость величин Sk от времени рассчитывается по приближенным формулам.

Объем данных (5, 6), собранных во время одной и той же реализации режима гравитационной ориентации, велик, поэтому перед подгонкой к ним решения уравнений (1), описывающего фактическое движение корабля, проводилось их предварительное сжатие. Целесообразность сжатия данных измерений угловой скорости и его способ описаны в [7]. Способ состоит в следующем. Телеметрические значения каждой компоненты угловой скорости сглаживались дискретным рядом Фурье: последовательности точек (tn , i ), n = 1, 2, ..., N аппроксимировались выражениями

. .                  Z X V • П l( t — t. )

Х⁽ t ) = a i, L +1 ⁺ a L +2⁽ t ^- t 1) ⁺ L a i, I sin --- —1— , (8)

,          ,                         ,        t N^- t 1

где a_{i, l} — коэффициенты, и число L одинаково для всех i = 1, 2, 3. Это число не должно превосходить N – 2 и быть таким, чтобы выражения (8) позволяли достаточно точно аппроксимировать на отрезке t ₁ ≤ t ≤ t_N переменные ω _i системы (1) в ее решениях, описывающих возможные движения корабля [7]. Коэффициенты a_{i l} находились методом наименьших квадратов. Точность аппроксимации данных ( t_n , _i ) выражением χ _i(t) характеризовалась соответствующим среднеквадратичным отклонением s _{ω i} .

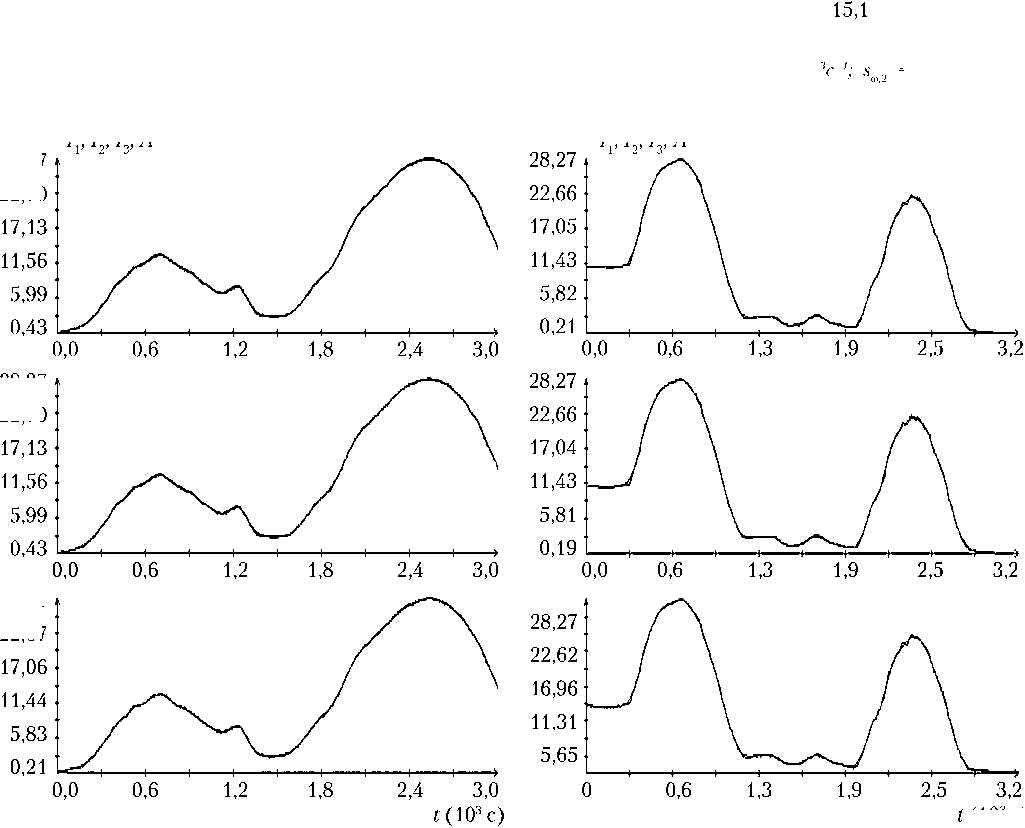
Графики данных (5) и графики сглаживающих эти данные выражений (8) для одной из реализаций режима гравитационной ориентации приведены на рис. 1. Графики данных расположены в левой части рисунка. Это — ломаные, звенья которых соединяют соседние по времени точки ( t_n , _i ).

Выражения (8) построены при L = 60. Их графики расположены на рисунке справа. Величины N , s _{ω, i} и декретное московское время (ДМВ) точки t ₁ приведены в подписи к рис. 1.

С помощью выражений (8) вычислялись псевдоизмерения — совокупность чисел

( l ^-1)( t N ^- t i)

t¹" t ^{1 +}       4L        ’

®(z) = Xi(t)) (1 = 1, 2,..., 4L +1; i = 1, 2, 3), используемых при обработке вместо исходных данных. Чтобы не усложнять обозначений, далее будем считать, что данные (5) — это псевдоизмерения.

Похожим образом псевдоизмерениями заменялись и измерения тока (6). Эти измерения разбивались на отрезки, соответствующие освещенным Солнцем участкам орбиты корабля. Совокупности точек ( ,   ) для значений , попавших в один и тот же отрезок, сглаживались выражением χj(t) при L = 60 (j = 1, 2, 3). Примеры двух отрезков измерений и сглаживающих выражений (8) иллюстрируются графиками на рис. 2.

В подписи к рис. 2 приведены число M точек на данном отрезке, среднеквадратичные значения s_{I, j} разностей    – χ _j( ) и ДМВ точки .

При выб ^, ранном масштабе рисунков оба графика практически сливаются, что согласуется с приведенными значениями s_{I, j} .

ω ₁ , ω ₃, ω ₃(10^–3с^–1)

-1,984

-2,167

-2,350

-2,533

-2,716

-2,899

А^У^

0,0     5,0      10,1     15,1     20,1    25,1

χ 1, χ 2, χ 3 (10^–3с^–1)

0,0

5,0      10,1

15,1     20,1    25,1

1,373

0,824

0,275

-0,275

-0,824

-1,373

у/; "У 3

0,0     5,0      10,1     15,1     20,1    25,1

0,0

5,0      10,1

15,1     20,1    25,1

1,373

0,855

0,336

-0,183

-0,702

-1,221

■м Г .

1,391

0,0      5,0      10,1     15,1      20,1     25,1 I

7(1О3с)

20,1    25,1

7(1О3с)

= 0,063 ⋅ 10^–3c^–1;

0,0

I I I А

I I I А

Рис. 1. Измерения угловой скорости и их аппроксимация: N s _{ω , 3} = 0,064 ⋅ 10^–3c^–1; момент t = 0 отвечает 13:53:07 ДМВ 08.02.2014 г.

5,0      10,1

= 2 515; s _{ω , 1} = 0,060 ⋅ 10^–3

t (103 с)

28,27

22,70

28,27

22,70

28,29

22,67

а)

Рис. 2. Измерения тока солнечных батарей и их аппроксимация: a – M = 3 040; s_{I, 1}

б)

= 0,076 А; s_{I, 2}

момент t = 0 отвечает 16:20:06 ДМВ 07.03.2014 г.; б – M = 3 175; s_{I 1} = 0,129 А; s_{I 2} = 0,129 А; s_{I 3} отвечает 13:46:43 ДМВ 08.02.2014 г.                               ^{,             ,             ,}

₂ = 0,075 А; s_{I, 3} = 0,077 А; = 0,130 А; момент t = 0

С помощью построенных сглаживающих выражений данные (6) на отрезке заменялись псевдоизмерениями =   + lh;    = χj ( ), где h = 20 с, l = 1, 2, ... и принадлежат отрезку сглаживания. Далее предполагается, что данные (6) — это псевдоизмерения. При фиксированном m величины (j = 1, 2, 3) почти одинаковы, поэтому измерением тока в момент считается величина Im = [I^ +122™) +13m)]/3.

Сначала совместная обработка данных измерений (5, 6) была выполнена по схеме, описанной в [3], и дала неплохие результаты. Однако, как показано в [3], измерения (6) содержат составляющую, которая обусловлена светом, идущим от поверхности Земли, и для которой нет простого и точного расчетного аналога. С другой стороны, данных измерений (5) оказалось достаточно для определения движения корабля. Ниже приведены результаты такого определения только по этим данным, данные (6) использовались для проверки.

Определением движения корабля по значениям угловой скорости (5) будем считать решение уравнений (1), доставляющее минимум функционалу ф-£ {f [ ^ - ® и иNA2};

. N                           (9)

A. = — 52 [го ⁽. n ) - го ( t )], i N ni i^{v n}^

где ∆ _i — постоянное смещение в данных (5) для i -ой компоненты угловой скорости. Функционал Φ получен в результате преобразования стандартного функционала метода наименьших квадратов, возникающего при уравнивании соотношений ≈      +   ( i = 1, 2, 3;

n = 1, 2, ..., N ). Минимизация Φ проводится по начальным условиям решения в точке t ₀ ( t ₀ ≤ t ₁), задаваемым величинами γ _b , δ _b и β _b , ω _{i 0} = ω _i ( t ₀), и параметрам ε , p_i , всего — по 10 переменным.

Минимизация функционала (9) выполнялась в несколько этапов. На заключительном этапе использовался метод Гаусса – Ньютона [9]. Чтобы обеспечить его надежную сходимость, надо иметь достаточно точное начальное приближение точки минимума и предусмотреть возможность регуляризации процесса минимизации. Регуляризация сводилась к использованию метода Левенберга – Марквардта [9] перед переходом к методу Гаусса. Поиск начального приближения состоял в минимизации Φ на движениях (4) при δ = π. В этом случае функционал зависит только от двух переменных — γ0 и Ω. Минимизация этого упрощенного функционала проводилась сначала случайным перебором в прямоугольнике 0 ≤ γ0 ≤ 2 π; Ωmin ≤ Ω ≤ Ωmax, где Ωmin и Ωmax — заданные числа. Приближенное значение Ω известно, поэтому разность Ωmax – Ωmin бралась малой. После перебора 500 вариантов применялся метод Левенберга – Марквардта. Найденное движение (4) позволяло задать начальную точку минимизации функционала (9) на решениях уравнений (1).

Точность аппроксимации данных измерений (5) и разброс в определении оцениваемых параметров будем характеризовать, следуя методу наименьших квадратов, соответствующими стандартными отклонениями. Хотя теоретиковероятностные допущения метода наименьших квадратов в данной ситуации не выполнены, стандартные отклонения оказались полезными характеристиками. Стандартное отклонение ошибок в данных (5) обозначим σ , оно рассчитывается по формуле о = V Ф _т1п/(3 N - 10); стандартные отклонения начальных условий и параметров обозначим σ_γ , σ_δ , σ_β , σ_{ω i} , σ_ε , σ _pi ( i = 1, 2, 3).

Результаты определения движения корабля

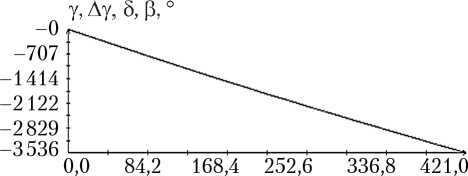
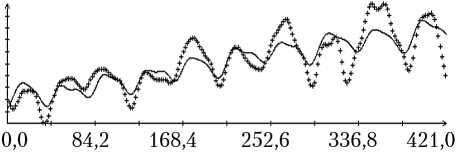
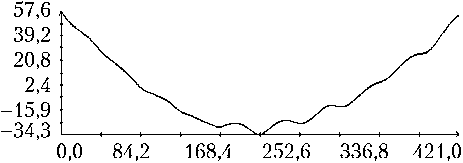
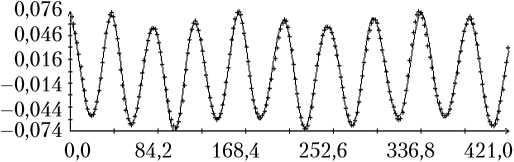
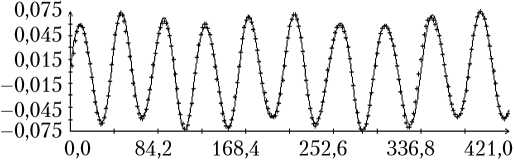
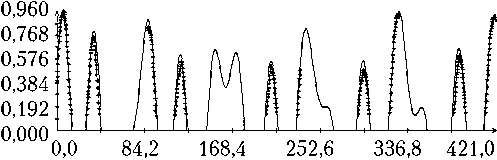
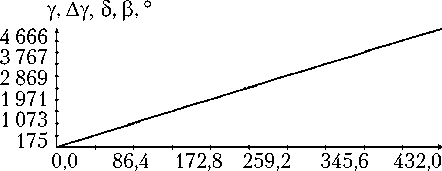
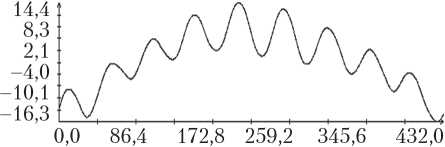
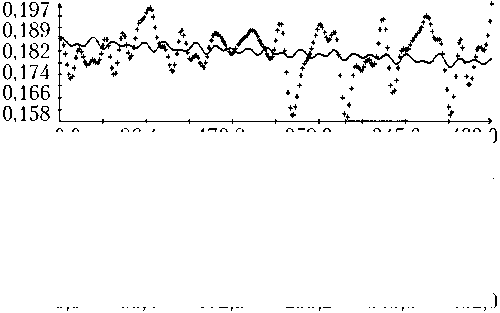
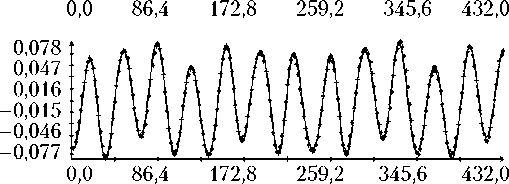
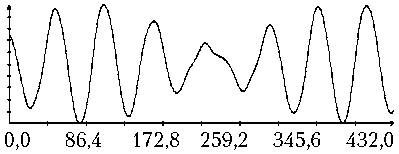
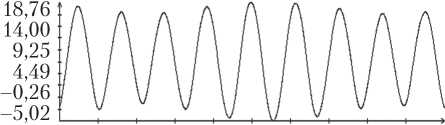
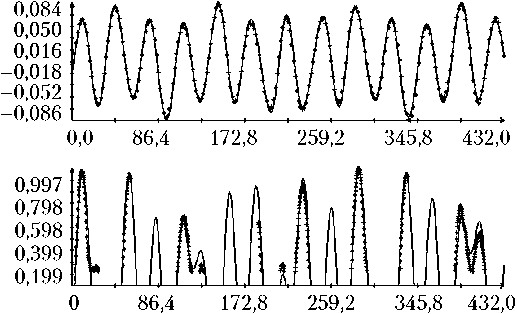
Определение вращательного движения корабля «Прогресс М-20М» по измерениям угловой скорости было выполнено для всех трех реализаций режима гравитационной ориентации. Результаты двух реализаций приведены на рис. 3, 4. Рисунки организованы следующим образом. В их левых частях изображены графики зависимости от времени углов γ , δ , β, а также график разности ∆γ ( t ) = γ ( t ) – с ₀ – с ₁ t , где с ₀ – с ₁ t — линейная аппроксимация функции γ ( t ), построенная методом наименьших квадратов. В правых частях этих рисунков помещены графики компонент угловой скорости ω _i ( t ) в найденных решениях уравнений (1) и функции η ( t ). Рядом с графиками компоненты угловой скорости ω _i ( t ) маркерами указаны точки ( t_n, _i – ∆ _i ), n = 1, 2, ..., N ; рядом с графиками функции η ( t ) — точки ( , I_m / I ₀), m = 1, 2, ..., M, для которых I_m > 3 A . Представленные на рисунках решения построены на отрезках t ₀ ≤ t ₁ ≤ T , где – 10 c; T = max( t_N , ) + 10 с. Моменты t ₀ на рисунках приняты за начало отсчета времени t = 0.

Как видно из рис. 3, 4, движения корабля близки движениям вида (4) при δ = π . Найденные решения уравнений (1) достаточно хорошо аппроксимируют данные (5), графики функции η ( t ) хорошо согласуются с данными (6). Однако следует отметить, что уравнения (1) описывают не все детали движения корабля. Это видно по графикам компоненты угловой скорости ω ₁. С другой стороны, диапазон изменения ординат этих графиков в несколько раз меньше аналогичного диапазона компонент ω ₂ и ω ₃, поэтому первое впечатление о больших значениях разностей ₁ – ∆ ₁ – ω ₁( t_n ) обманчиво.

-0,124

-0,133

-0,142

-0,151

-0,160

-0,169

ω₁ , ω₂, ω₃ , ° /с; η

185,77 ♦ 183,48 \ 181,19 \ 178,90 \ 176,61 \ 174,32 —^ 0,0

84,2   168,4 252,6   336,8 421,0

-2,01

-3,42

-4,84

-6,25

-7,67

-9,08

wV^/yvw

0,0   84,2   168,4 252,6   336,8 421,0

t , мин

t , мин

Рис. 3. Движение корабля в режиме гравитационной ориентации: момент t = 0 отвечает 13:52:03 ДМВ 08.02.2014 г.

ω₁ , ω₂, ω₃ , ° /с; η

188,55 185,01 181,48 177,94 174,40 170,86

0,0 86,4   172,8 259,2 345,6 432,0

t , мин

t , мин

Рис. 4. Движение корабля в режиме гравитационной ориентации: момент t = 0 отвечает 14:22:26 ДМВ 09.02.2014 г.

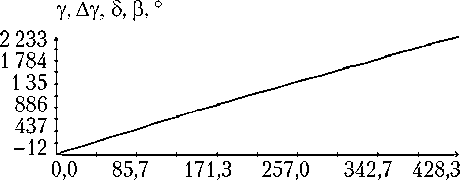
Приведем некоторые количественные характеристики. Поведение функционала (9) в окрестности точки минимума можно характеризовать собственными числами и векторами матрицы системы нормальных уравнений, возникающей в методе Гаусса – Ньютона. В точке минимума, где следует вычислять перечисленные величины, эта матрица приближенно совпадает с матрицей квадратичной формы d ² Φ /2. Как оказалось, для выполненных определений движения собственные числа указанной матрицы имеют примерно одинаковые значения. Например, для варианта определения движения, приведенного на рис. 5, указанные собственные числа составляют (в порядке возрастания) 1,467; 10,50; 110,2; …; 24 347; 7 423 000. Собственный вектор, отвечающий минимальному собственному числу, имеет вид:

(0,102; 0,133; 0,073;–0,022; –0,143; –0,039; 0,972; 0,000; 0,001; 0,000) ^Т .

В этом векторе доминирует седьмая компонента, отвечающая параметру p ₁. Следовательно, этот параметр определяется наименее точно. Такое доминирование имеет место и для двух других случаев определения движения корабля.

Точность определения движения корабля характеризуется стандартными отклонениями начальных условий. Если начальные условия задаются вне интервала с обрабатываемыми измерениями, то их значения обычно превышают стандартные отклонения фазовых переменных в средней части интервала. Эти стандартные отклонения приведены в табл. 1. Угловые переменные в таблице выражены в радианах. Стандартные отклонения углов γ _b , δ _b и β _b не превосходят 1,5 ° . Оценки параметров модели и их стандартные отклонения приведены в табл. 2. Как видно из этой таблицы, параметр p ₁ определен наименее точно.

ω₁ , ω₂, ω₃ , ° /с; η

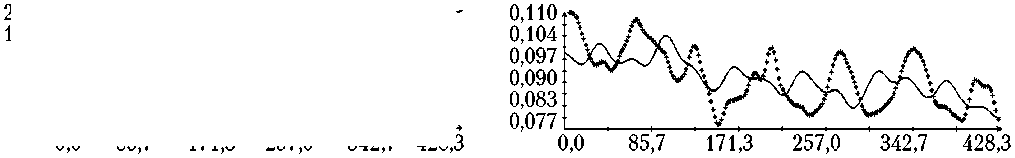
21,5 10,6 -0,2 -11,1 -21,9 -32,7 185,85 183,58 181,31 179,04 176,77 174,50 13,68 9,60 5,53 1,45 -2,62 -6,70	/Л                        0,076 0,046 V\a      0,016 -0,015 __/                              \   -0,045 CL_____._____._____._____._____._____._____._____.____\    -0.075			>+
	),0    85,7    171,3 257,0		342,7 428,3          С л      0,077 1	),0     85,7		171„	3    257,С	342,7   428,3
	),0   85,7    171,3 257	,0	342,7 428,3          ( 0 995 Nt 1	),0 Е	!5,7	171,.	3    257,(	342,7   428,3
				),0     85,7		171,3    257,0    342			,7   428,3 t , мин
	),0    85,7    171,3 257,0		342,7 428,3          ( t , мин

Рис. 5. Движение корабля в режиме гравитационной ориентации: момент t = 0 отвечает 14:40:58 ДМВ 07.02.2014 г.

Таблица 1

Оценки точности определения движения корабля

Номер интервала	Дата	tN – t 1 , мин	σ, 10–3 c–1	σ γ	σδ	σβ	σ ω1 , 10–3 c–1	σ ω2 , 10–3 c–1	σ ω3 , 10–3 c–1
1	07.02.2014	423	0,108	0,022	0,013	0,0087	0,0059	0,017	0,028
2	08.02.2014	418	0,078	0,019	0,014	0,0059	0,0044	0,013	0,022
3	09.02.2014	432	0,102	0,020	0,012	0,0073	0,0072	0,017	0,022

Оценки уточняемых параметров

Таблица 2

Номер интервала	∆ 1 , 10–3 c–1	∆ 2 , 10–3 c–1	∆ 3 , 10–3 c–1	p 1	σ p 1	p 2	σ p 2	p 3	σ p 3	ε	σ ε
1	0,073	–0,045	–0,017	0,064	0,087	–0,016	0,0017	–0,018	0,0021	–0,0108	0,00032
2	0,074	–0,005	0,081	0,176	0,061	0,024	0,0031	0,054	0,0045	0,0135	0,00062
3	0,077	–0,054	–0,008	0,270	0,084	0,003	0,0077	–0,010	0,0082	–0,0046	0,00027

Выводы

Полученные результаты позволяют сделать вывод, что движение ТГК «Прогресс» в режиме гравитационной ориентации вращающегося спутника может быть надежно определено по данным измерений вектора его угловой скорости. Режим обеспечивает устойчивое угловое движение ТГК и достаточный приход электроэнергии даже в случае нахождения Солнца вблизи плоскости орбиты корабля. Расчеты остаточных микроускорений на борту в этом режиме показывают [2, 10], что рассматриваемый режим обеспечивает комфортные условия для выполнения многих экспериментов в области микрогравитации.

Закрутки ТГК на Солнце вокруг нормали к плоскости солнечных батарей [3] или вокруг близкой к этой нормали главной центральной оси максимального момента инерции корабля [4] обеспечивают устойчивое вращение и практически максимальный энергосъем. Изменяя угловую скорость вращения ТГК, можно обеспечивать калибровочные значения микроускорений, что важно при планируемом изучении конвективных течений с помощью научной аппаратуры «Дакон» [1, 3, 4].