Отражение рентгеновского пучка от ограниченной многослойной дифракционной решетки

С появлением новых подходов к задачам рентгеновского рассеяния на многослойных дифракционных решетках (МДР) совершенствуются методы анализа дифракционных данных, в частности, все интенсивнее используется картографирование интенсивности рассеяния в обратном пространстве. Традиционно когерентное рассеяние на МДР описывается в рамках пространственно неограниченной рентгеновской волны, при этом дифракционные порядки становятся бесконечно узкими в латеральном направлении. Такой теоретический подход к задачам картографирования не применим. Поскольку в экспериментальных исследованиях рентгеновские пучки латерально ограничены, необходим новый формализм для рассмотрения дифракционной задачи. Работа по- священа развитию теории дифракции от МДР сис-пользованием нового подхода.

Теория

Пусть на МДР, состоящая из NΛ числа периодов шириной Л (рис. 1), под углом Д 1 к оси x падает монохроматическое синхротронное излучение с длиной волны λ. Считаем, что фронт падающей волны ограничен и имеет поперечный размер s1. Штрихи дифракционной решетки параллельны оси y, а ось z нормальна к поверхности образца и направлена вверх. Период многослойного рентгеновского зеркала (МРЗ) обозначим параметром d, общую толщину – sz, а толщину вытравленной ча- сти МРЗ – szg. Найдем интенсивность отраженной

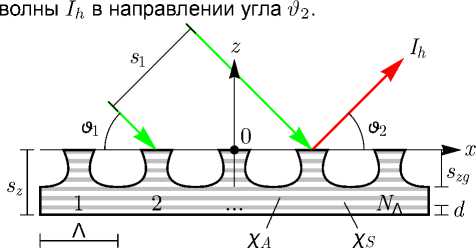
Рис. 1. Схема отражения рентгеновского пучка от ограниченной МДР.

Fig. 1. X-ray beam reflection scheme on the bounded multilayer grating.

Математическая модель рентгеновской поляризуемости МДР x = ( X A a + X S (1 - a))b зависит от функции a( z ) , которая моделирует распределение слоя поглотителя в объеме МРЗ, и функции b( x,z ) , позволяющей описать рельеф МДР. Считаем, что слой поглотителя и разделителя находится в аморфном состоянии, и их поляризуемости равны x A и X S соответственно. Функция a равна единице в слое поглотителя и равна нулю в слое разделителя. Функция b равна единице внутри отражающей полосы и нулю – за ее пределами. В приближении двух сильных волн считается, что в объеме МРЗ распространяется проходящая волна, поле которой имеет вид E ₀ ( r ) = A ₀ ( r ) e i ^k 0 ^r , и дифрагированная - E _i ( r ) = A _i ( r ) e i ^{k 1} r . Здесь k ₀ - волновой вектор падающей волны, | k ₀ | = к = 2 п/Х - волновое число, k _i = k ₀ + h , h -вектор обратной решетки многослойной структуры, | h | = h = 2 п/d . Амплитуды A 0 , _i ( r ) являются медленно меняющимися функциями от пространственных координат. Формально из уравнения Гельмгольца ( △ + к 2 (1 + x ( r ))) E ( r ) = 0 можно получить следующую систему уравнений относительно неизвестных функций A 0 , _i ( C,z ) = (2 п ) ⁱ J dx A о , i ( x, z ) e -i^x :

(ddz - ^п п ( c )) a n ( ^,z )

n

^ ia nn dC b( C ,z ) -A n ‘ ( C - C ,z ) • ^′ =0 , 1

Здесь индекс n равен 0 или 1. Пределы интегрирования от -го до + го . В уравнениях (1): b -Фурье образ функции b , n n ( C ) = [ nh ( к sin Д 1 -nh/ 2) - C ( k ^cos Д 1 + C/ 2)] / ( nh - к sin Д 1 ) , a _n,_n ‘ = к ² X n-n ‘ / (2 nh- 2 к sin Д i ) , X n = X S sinc( nn ) + ( x A -X S )sinc( nnY ) е^{г пп}^ - Фурье коэффициенты рентгеновской поляризуемости МРЗ, γ – отношение толщины слоя поглотителя к периоду МРЗ. Заметим, что система перевязанных интегро-дифференциальных уравнений (1) зависит только от параметра Д 1 . Граничные условия задачи: A ₀ ( C, 0) = ( A 1 s 1 / sin Д i ) sinc( Cs 1 / (2sin Д 1 )) и A i ( C, -s z ) = 0 . Так как амплитуды A 0 , _i ( x,z ) имеют компактный носитель на оси x , то согласно теореме Котельникова их Фурье образы можно записать в виде ряда:

An(C, z) = ^ An(Cm’, z) sinc(BC - пт'), (2) m′ где Cm = nm/B - эквидистантные отчеты на оси C, пределы суммирования от -го до + го. Произвольная величина B = ЛNB/2 характеризует компактность носителя функций A0,i(x,z), NB - подходящее целое число. Подставим ряд (2) в систему уравнений (1). Запишем полученные уравнения в матричной форме, ограничившись числом неизвестных функций A0,i(Cm, z):

^d A dzz ⁾ = M ( z ) . A ( z ) • (3)

Здесь вектор A ( z ) = ( A o ( z ) A i ( z )) T , ( A o , i ( z )) r = A 0 , _i ( C r ,z ) , блочная матрица M ( z ) состоит из квадратных матриц ( M _ii ( z )) r,c = n 0 ( C r ) ^ rc + a о , о B r-c ( z ) , ( M i2 ( z )) r,c = a о , i B r—c ( z ) , ⁽-^^ 2i ^{( z} )) r,c a i , 0 ^B r-c ^{( z} ) , ⁽-^^ 22 ^{( z} )) r,c

П _i ( C r ) 5 _rc + a _i , _i B _r-c ( z ) , индексы строки r и столбца c пробегают значения от – M до M , 5 _rc - символ Кронекера, B _m ( z ) = Г( z ) /N B sinc( пт Г( z ) /N B ) L N ( пт/N B ) , L N ( x ) = sin( Nx ) / sin( x ) , N = min( N B , N л ) -эффективное число периодов МДР. Функция Г( z ) задает модель формы отражающих полос и равна отношению ширины отражающей полосы к периоду МДР на глубине z . В области z < -s zg функция Г( z ) = 1 . Уравнение (3) решается численным методом. Интенсивность отраженной волны в направлении угла Д ₂ (рис. 1) равна I _h = | к sin Д ₂ 2A _i ( q _x , 0) | , где q _x = к (cos Д ₂ - cos Д _i ) - проекция на ось x отклонение вектора рассеяния от узла обратной решетки, q _z = к (sin Д _i + sin Д ₂ ) - h . Для частичной суммы по m в выражении (2) необходимо, чтобы M >  B|q x 1/п .

Численное моделирование

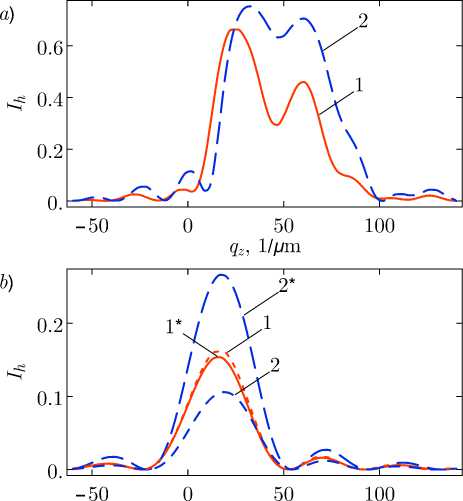
Численное моделирование проводилось для Ni/C МДР c параболической моделью формы отражающих полос [1] (Гb = 1, Гt = 0,4, Гт = -0,21). В вычислениях были использованы следующие значения параметров: Х = 0,154 нм, d = 3,9 нм, γ = 0,37, sz = 0,273 мкм, szg = 0,156 мкм, Λ = 0,8 мкм. Численный эксперимент проведен в двух конфигурациях (рис.2). В первой конфигурации пучок полностью засвечивал 41 период МДР, во второй – узкий пучок шириной 0,648 мкм испытывал дифракцию на МДР с большим числом периодов. На рис.3 представлены карты распределения интенсивности рассеяния в обратном пространстве для первой и второй конфигурации эксперимента. На рис.4 показаны сечения этих карт вдоль оси qz при разных значе-

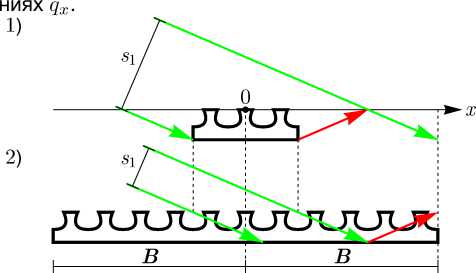
Рис. 2. Схема 1-й и 2-й конфигурации численного эксперимента.

Fig. 2. Diagram of the first and second configurations of a numerical experiment.

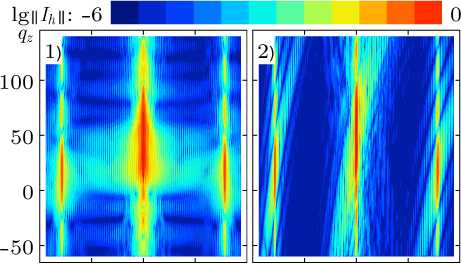
Рис. 3. Карты функции 1g I h ( q x ,q _z ) для 1-й и 2-й конфигурации численного эксперимента.

Fig.3. Maps of the function 1g I h ( q x , q z ) for the first and second configurations of a numerical experiment.

Распределение интенсивности рассеяния в обратном пространстве для первой и второй конфигурации существенно отличаются друг от друга не только вдоль оси q x , но и вдоль q z -сечений. В случае первой конфигурации МДР «купается» в падающем пучке. Поэтому фактор засветки поверхности решетки не влияет на RSM. В отличие от этого случая для второй конфигурации фактор засветки имеет существенное влияние. Точный учет параметра sin ϑ 1 в вычислениях приводит к тому, что для второй конфигурации численного эксперимента кривые отражения вдоль q x = -k Λ и q x = k Λ , где k Λ = 2 π/ Λ , имеют разную высоту и ширину максимумов, в то время как на картах, рассчитанных по упрощенным формулам [2], сателлитная структура была симметричной. Это можно связать с нелинейностью функции 1 / sin ϑ 1 от q x и q z для Ni/C МДР, у которой угол Брэгга составляет примерно 1°.

q z , 1 / pm

Рис. 4. Сечения карт вдоль оси q z для первой (кривая 1) и второй (кривая 2) конфигурации численного эксперимента: a) q x = 0 ; b) q x = к л и q x = -к л ( * ) - Fig. 4. The RSM sections along the q z axis for the first (curve 1) and second (curve 2) configurations of a numerical experiment: a) q x = 0 ; b) q x = к л and q x = -к л ( * ) -

Работа выполнена при частичной финансовой поддержке Программы фундаментальных исследований УрО РАН (проект 18-10-2-23) и РФФИ (проект № 17-02-00090).