Отыскание нетривиального решения интегрального уравнения Салема
Автор: Давлатов Ш.О.
Журнал: Мировая наука @science-j
Рубрика: Основной раздел
Статья в выпуске: 5 (98), 2025 года.
Бесплатный доступ
Эта статья посвящена исследованию нетривиального решения интегрального уравнения Салема. Для отыскания нетривиального решения интегрального уравнения рассмотрены все возможные случаи. И во всех случаях показано, что интегральное уравнение имеет только тривиальное решение.
Последовательность, уравнения салема, нетривиальное решение, гипотеза римана
Короткий адрес: https://sciup.org/140311526
IDR: 140311526
Текст научной статьи Отыскание нетривиального решения интегрального уравнения Салема
7£2№^=о
л (1)
среди ограниченных и измеримых функций имеет только тривиальное решение для 0< ст <1, .
Покажем, что среди ограниченных и измеримых функций интегральное уравнение (1) имеет только тривиальное решение .
В интеграле (1) сделаем замену переменных .
После замены интеграл (1) имеет вид:
z^(z)dz
о
Выберем произвольное значение
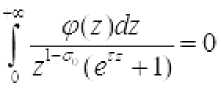
. Тогда
Докажем, что интегральное уравнение (3) не имеет нетривиальных решений.
I. Возьмем ограниченную, измеримую функцию заданной почти всюду на К с] и удовлетворяющей условию
^(z)dz = | (p(z)dz. b^(a.с}
Покажем, что при любых т > О
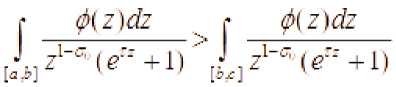
где .
Действительно, из неравенство
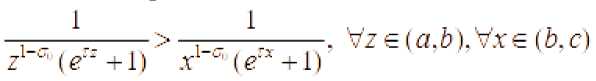
следует, что
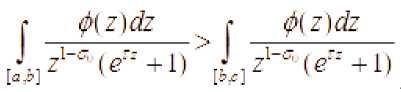
-
II. Рассмотрим теперь ограниченную, измеримую функцию заданная почти всюду на [л, с] и удовлетворяющая условии:
-
3. [-]
где
Построим функцию
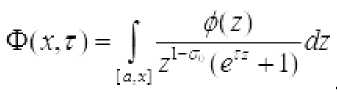
почти всюду на [л. У почти всюду на [^У]
ф^ IM
, dz z (ег -Г)
где
a
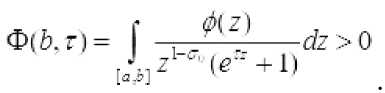
Из 3-го условия следует, что
Ф(с.1) = f -- dz- Г -J-J— dz<0
Очевидно, что для любых ij ^ii верны соотношения
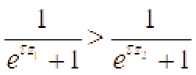
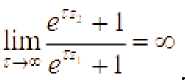
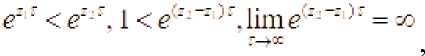
Из этого следует, что ростом Z , начиная с некоторого значения , функция начинает возрастать. Следовательно существует точка r = ^ - такое, что Фк. r:. . Очевидно, что и для всех r > - функция . Это означает, что существует точка такое, что n Г liiii Ф(с. г) — 0
функция достигает максимум в этой точке, поскольку .
-
III. Аналогичное рассуждение ведется для ограниченной, измеримой функции заданная почти всюду на [л, с] и удовлетворяющая условии: 1. ^ z )< О почти всюду на[«.&],
почти всюду на
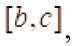
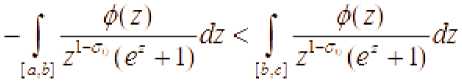
где
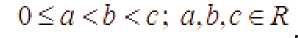
Аналогично, построим функцию
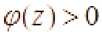
ф(х,г)= | -рДУ—^7z , где а <х <с; . Очевидно, что Ф(х, г непрерывная функция
Ф(Ь.г)= I । - ---dz<0
Из 3-го условия следует, что
Ф(^.П
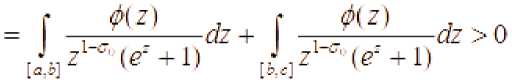
Следовательно, ростом 2 , начиная с некоторого значения
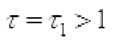
у ■ ► начинает убывать. Следовательно, существует точка такое, что . Очевидно, что и для всех функция
1Ш1Ф(СГ) = 0 т=г>г и г—= . Это означает, что существует точка такое, что функция Ф( с. г достигает минимум в этой точке.
-
IV. Пусть ограниченная, измеримая функция заданная почти (0. +=о)
всюду на и удовлетворяющая условию
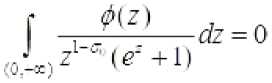
Рассмотрим функцию
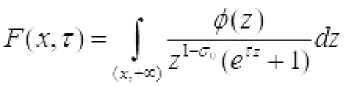
Рассмотрим возможные случаи, учитывая, что
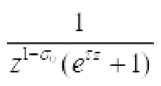
убывающая, положительная функция. Покажем, что во всех случаях функция m г)
имеет, по крайней мере, одну экстремальную точку. Все условия в этих случаях обеспечивают возможность появления хотя бы одного экстремума функции .
1 ЛО.г)
1-случай. Пусть интеграл представлен в виде конечной суммы интегралов
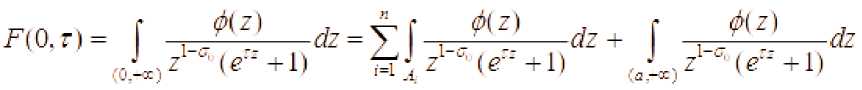
где
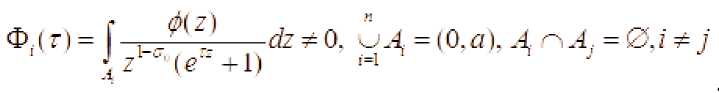
. Интегралы
функция знака постоянно на
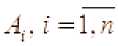
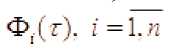
знака
чередующие, упорядоченные по интервалу интегрирования.
Пусть ФЛГ? '■ . Рассмотрим случай
-
1. Если '■ - четный
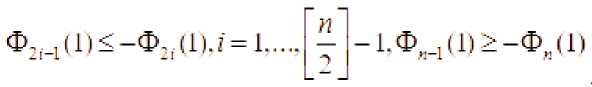
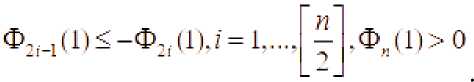
-
2. Если Vt - нечетный
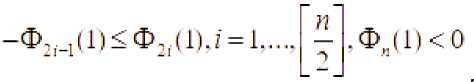
В этом случае из III. следует, что существует точка 1
такое, что
Откуда
.
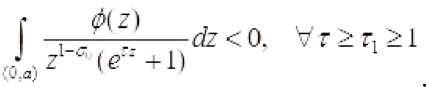
В этом случае из II. следует, что существует точка ; - - такое, что
Откуда
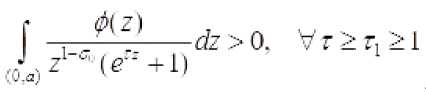
Следовательно, из II. следует, что существует точка
m^j >o
ЛО, г)
. Откуда следует, существование точки
LimF(O,r) = O
такое, что
- , в которой функция
достигает максимум, так как
Пусть теперь V 4 . Рассмотрим случай
1. Если ?' - четный
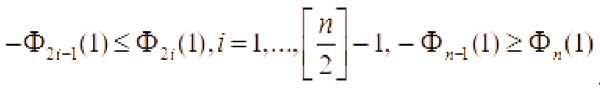
Следовательно, из III. следует, что существует точка 1 такое, что
/ (0. rj \ . Откуда следует, существование точки г ^ , в которой функция
no T) limF(O.D = O достигает минимум, так как -—i
В остальных случаях, очевидно, что функция ЛО. г имеет, хотя бы одну экстремальную точку.
2-случай. Пусть существует последовательность точек
1цихи = a
' Y ■ Y ‘ i7 Л = L "^ ^ я—11
("л / ' .4 " U’ , сходящейся к точке a справа, т.е. . Эти точки, разбивают отрезок [й' ‘-I на отрезки. В этих отрезках функция знака постоянна. почти всюду на (0. , в частности .
Пусть
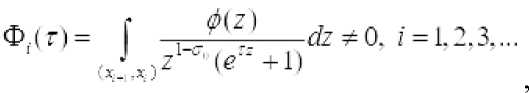
знака чередующие интегралы и
.
В этом случае интеграл F(0. г можно представить в виде бесконечной суммы интегралов т.е.
HO,r) = f ^£^ = УФ,(Г)+ [ ^J^dz
Пусть
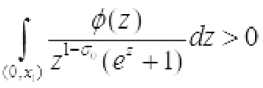
тогда из (4) следует
F(.rl>= f 4^1--dz<0
.
Не нарушая обычности можно считать, что Ф1 (1) >■ 0
Ф.Ш. 1=1. 2. 3....
Пусть среди интегралов л t имеются интегралы удовлетворяющие условие
.
Тогда из II. следует, что существует точка такое, что
Ф:^<Г11 + ФЧ(’1)>Ф,,1.1(1) + Ф,,1(1| или
Ф;.,-!^!-®:./^^0- *“L23
или
Вообще та
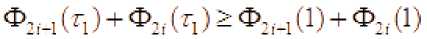
«WriH^-T'^ «-bJ-J
Ф1(г1) + 1’(х1.г1)>Ф1(1) + /’(х1.1)
или
.
Откуда
,
Следовательно F(0, zj) >F(0, . Откуда следует, существование точки г = rt > У , в которой функция F(0. г достигает максимум, так как limF(O.r) = O
.
Аналогично, пусть тогда из (4) следует
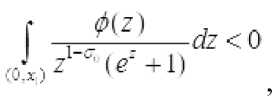
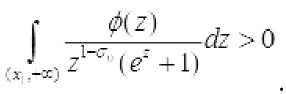
Не нарушая обычности можно считать, что ф10>< . Пусть среди
Ф г =1 2 3 интегралов ‘ имеются интегралы удовлетворяющие условие
.
Тогда из III. следует, что существует точка = - > такое, что Ф^^ + Ф^Л^Ф^Ш+Ф,,/!)
или
.
Вообще та
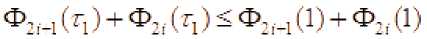
или
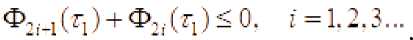
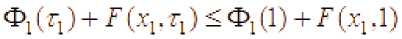
или
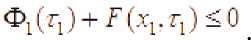
Откуда
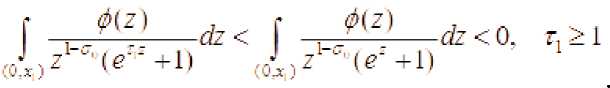
Следовательно НО: Н <Н°> . Откуда следует, существование точки Г = Г. > ^ , в которой функция F(0, г достигает минимум, так как LimF(O,r) = O
Пусть существует две последовательности точек {л-кд; >д}п = 1,2Д... {bob >Ь. к = [.2,3,... , сходящейся к точкам ,
liin х = а Ши у. = Ъ я—»х “ я—»®*’ " А справа соответственна, т.е. *т>а , . , для всех и, .
Эти точки последовательностей , разбивают отрезок [д- >1 на отрезки. В этих отрезках функция знака постоянна. почти всюду на (0. , в частности .
Пусть
Ф,(П- f т^^---dz^O. i = 1.2.3....
Л/ "(e +1> ,
*',
знака чередующие интегралы и не нарушая обычности можно считать, что .
В этом случае интеграл F(O, г можно представить в виде бесконечной суммы интегралов т.е.
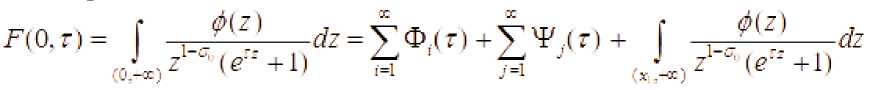
Пусть
[ i_ ^Z^---> О тогда из (4) следует
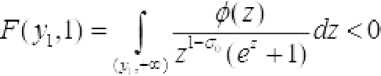
Не нарушая обычности можно считать, что x I
В этом случае из II. следует, что существует точка такое, что
Т^МЧ^и^^^
или
.
Если Ф1(1)>0,.
♦:«( M+*з W ^н (1)+M)
или
«ViW + IU^O. :=l-2.3....
А если ®i(D<0 ,
Ф:,^) + ®m(4) г Фг,(1) +
.
’Р1(г1)+Г(11.!'1)гЧ'1(1)+Г(112) или
.
Откуда
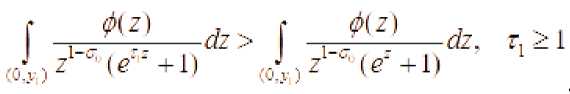
Следовательно И > Ж: . Откуда следует, существование точки Г = Гк > Г; , в которой функция F(O. ; достигает максимум, так как limF(0,r) = 0
Аналогично рассматривается случай
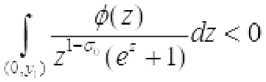
В этом случае, аналогично рассуждая можно показать, существование точки г = rt > ^ , в которой функция F(O. г достигает минимум.
Остальные этому подобные случаи, рассматриваются аналогично.
3-случай. Пусть интеграл F(O. г представлен в виде бесконечной суммы интегралов
ЛО.г) = f Hf.F1 dz
^z (e = +l) "(e‘--ll , ( где
Фг (И = f —dz * °- = < о- +* >. 4 n J. =0j^j
■ z (e+l) 1=1 ■
^(z) J . i=1.2.3.... Ф.(г). i =1.2.3....
знака постоянно на x . знака чередующие интегралы, упорядоченные по интервалу интегрирования.
Пусть ФИ? '■ . Из условия (4) следует, что среди интегралов
Ф г =1 2 3
имеются интегралы удовлетворяющие условие
Ф.,1Ч(1)<-ФЧ(1). £ = 1.2.3
J r — T" 1
1 такое, что
Фч-А»-,*Ч<Г1>> * = L2-3-
Следовательно, f (o. n -■ . Откуда следует, существование точки r = r. , в
которой функция достигает максимум, поскольку .
Пусть теперь ФА)< . Аналогично, из условия (4) следует, что среди
Ф i =12 3
интегралов имеются интегралы удовлетворяющие условие
-Ф214(1)£Ф,, (1), £ = 1.2.3...
J r — у 1
1 такое, что
-‘tw^
Следовательно, M 0 - ^j) . Откуда следует, существование точки
, в
по г) LimF(O,r) = O которой функция к ► достигает минимум, поскольку .
Из этих фактов следует, что функция F(O. г принимает различные значения при различных значениях .
Из выше изложенных следует, что в среди ограниченных измеримых функций о( интегральное уравнение (2) имеет только тривиальное решение. Следовательно, / (. почти всюду в .
Литературы.


