P-CVD-SWIN: a parameterized neural network for image daltonization

About 8 % of men and 0.5 % of women worldwide have color vision deficiency (CVD), which is an inability to distinguish between certain colors of the spectrum. Human color vision is based on three types of cones in the retina, which differ in their spectral sensitivity: long-wave sensitive (L), medium-wave sensitive (M), and short-wave sensitive (S) [1]. The absence of one type of the cones results in dichromacy, sometimes referred to as daltonism. It is divided into protanopia, deuteranopia, and tritanopia, which correspond to the absence of L-, M-, and S-cones, respectively. Anomalous trichromacy, caused by a deviation in the sensitivity of one type of the cones from the norm, also occurs. In its extreme form, anomalous trichromacy is close to dichromacy, so dichromats and anomalous trichromats close to them are collectively called protans, deutans and tritans.

To help people with CVD perceive images, methods have been proposed to preprocess them in order to compensate for the distortions introduced by CVD [2]. This approach can be compared to precompensation of refractive errors of vision [3]. It is important to note that such precompensation cannot provide the ability, for example, for a deuteranope to distinguish red and green colors, but it does improve the perception of contrasts and is capable of introducing the boundary between red and green areas (still not knowing which one is red and which is green). Such precompensation is called image daltonization.

The color space of a person with normal color vision (NCV) is three-dimensional, while that of a dichromat is twodimensional. The colors perceived by a dichromat can be simulated by removing from a vector in a three-dimensional color space a component that is indistinguishable to dichromats. The resulting two-dimensional vector for visualization by people with NCV must be supplemented with some third component, which can be chosen in different ways [4]. In general, this simulation can be described as a projection of the original vector in a three-dimensional linear color space along the direction of color blindness onto some two-dimensional color manifold. The requirement for the manifold is that the projection onto it in this direction exists and unique for any color. The most common approach is a projection onto a plane, as done in the work of Viénot [5], whose approach will be used in this paper.

The constructed image, which simulates the color perception of all pixels of the original, will be called a retinal image . The task of precompensation is to transform the original image so that the retinal image conveys the contrasts of the original as accurately as possible.

However, preserving contrasts in the image often leads to a violation of chromatic naturalness: objects acquire colors that are not characteristic of them. Chromatic naturalness can be considered in two aspects. Firstly, naturalness is important for the dichromat himself, i.e. the chromaticity in the retinal image after the precompensation must be close to the original chromaticity. Secondly, chromaticity may be important for a person with NCV. For example, a dichromat can watch movies together with people with NCV on the same device, so it is important that the precompensation does not disrupt the naturalness of the retinal image of the person with NCV (which we consider to be the same as the precompensated image that appears on the screen). This also called as visual sharing between CVD and normal-vision audiences [6].

A paper by Ma et al. [7] presents a method based on the construction of a nonlinear color map (SOM, self-organizing map), mapping a three-dimensional space of RGB colors into a two-dimensional color space, optimally preserving the contrast for a given image. However, this method does not preserve the naturalness of colors for people with NCV.

In a later work [8], Tennenholtz and Zachevsky proposed a method of natural contrast enhancement for dichromats, using similarity maps. The method produces local changes to the image around the zones where people with CVD have difficulty distinguishing colors and uses a color similarity map. The authors evaluated the proposed method on observers with CVD, but unfortunately did not provide source code to reproduce their results.

A paper by Simon-Liedtke and Farup [9] presents the Yoshi-II method, which operates on a scale pyramid using a gradient descent and improves the visibility of chromatic boundaries and contrast. The method preserves the naturalness of only neutral colors – those that remain distinguishable to people with CVD – rather than all colors. The authors also have not provided the source code.

The individualised halo-free gradient-domain colour image daltonisation algorithm [10] is a development of the previous work. It reduces the severity of artifacts near chromatic boundaries, increases the level of detail in the recolored image, and reduces the computational complexity of the algorithm. Unfortunately, the source code published by the author is intended for image precompensation not for a protanope, a deuteranope, or a tritanope, but for some imaginary dichromat modeled by the author.

A paper by Bao et al. [11] describes a color correction method for dichromats, using the CIE L*a*b* color space. The method is aimed at preserving the differences between red-green hues for protanopes and deuteranopes by increasing the differences along the b* axis, where the colors remain distinguishable. To achieve this, an optimization problem is posed and then solved by the conjugate gradient method. The source code is not provided.

In recent paper [12], a precompensation method is presented that aims to preserve the chromatic naturalness of the image for both NCV and CVD persons. The main idea is to modify the achromatic component using nonlinear contrastpreserving visualization method. At the same time, the chromatic components are kept close to the original. To compare their approach with the previously known methods, authors utilize objective and subjective evaluations that separately assess visibility enhancement and naturalness preservation.

A common drawback of all optimization methods is a fairly large and unfixed operating time, which makes it difficult to integrate them into real-time visualization systems (such as smartphone screens, TV sets, etc.). This contributed to the development of neural network methods for image daltonization, which have become widely used and in the field of image analysis [13].

In a paper by Orii et al. [14], a multilayer neural network with perceptual model was proposed. The authors trained a neural network consisting of a color map construction block and blocks of color discrimination characteristics for individuals with CVD. The method was evaluated visually on images simulated for protanopes. Authors provided neither the source code nor the training dataset.

Li et al. [15] first used a GAN (generative adversarial network) architecture to solve the problem under consideration. They adapted and compared three neural networks: pix2pix-GAN, Cycle-GAN, and Bicycle-GAN, and also created a dataset of 3084 images, allowing training, testing, and comparing various methods of image enhancement for persons with CVD. In their experiments, the best results were shown by the pix2pix-GAN neural network, which ensures color discrimination by an observer with CVD and simultaneously preserves the naturalness of colors for an observer with normal vision. However, the lack of publication of the collected dataset does not allow reproducing the results of this work. Additionally, it is worth pointing out one serious disadvantage of GAN architectures, which is that the learning process can be unstable [16].

Pendhari et al. [17] proposed a convolutional neural network architecture for precompensation. The authors trained three separate models for each type of CVD: protanopia, deuteranopia, and tritanopia. According to their illustrations, the proposed method does not preserve the naturalness of colors. The authors provided neither the source code nor the training dataset.

In a paper by Chen et al. [18], an architecture based on a U-Net is presented, in which convolutional layers are replaced by SWIN (Shifted WINdows) transformers [19]. Hereinafter, this architecture is referred to as CVD-SWIN. The paper investigated the problem of color precompensation with preservation of contrast and naturalness of colors, implemented by using a composite loss function: one addendum estimates the contrast (both local and global), and the other – chromatic naturalness using SSIM. Thus, CVD-SWIN is a state-of-the-art architecture for image daltonization that ensures the preservation of chromatic naturalness.

However, the CVD-SWIN approach has a serious disadvantage, which is the need to train separate neural network models for each type of dichromacy (protanopia, deuteranopia, and tritanopia). This disadvantage manifests itself in two aspects.

Firstly, the mathematical description of different types of dichromacy is uniform and differs only in the blind direction in the color space. Therefore, it can be assumed that the knowledge obtained by a neural network model trained on precompensation examples for one type of dicromacy can be used for the other types.

Secondly, as the number of trained models increases, so does the amount of computer memory required to store them. At the same time, in addition to the three directions of color blindness corresponding to protanopia, deuteranopia, and tritanopia, in some cases it makes sense to consider other directions. Thus, it is known that in people with NCV, the spectral sensitivity curves of the long-wave (L) cones can have the maximum at a wavelength of either 559 or 563 nm (the so-called polymorphism of the long-wave cones [20]). Obviously, the same polymorphic long-wave cones (and the corresponding color blind directions) are also found in the retinas of deuteranopes. In protanopes, the long-wave cones are absent, and in the spectral sensitivity curves of the medium-wave (M) cones of normal trichromats, no polymorphism is observed. However, there are known cases of the presence of defective pigments of the medium-wave cones in the retinas of protanopes [21]. Tritanopia is an extremely rare phenomenon, however, based on the independence of inherited defects, we can assume that a tritanope may well be the owner of a defective pigment of the L or M cones. Although the differences between the different variants of the cone spectral sensitivity curves are small, the above facts may indicate the need to consider more than one direction of color blindness for some types of dichromacy.

Thus, developing a neural network architecture similar to CVD-SWIN but parameterized by the color blindness direction will improve model training and potentially expand the applicability.

In this paper, such a parameterized architecture is proposed and investigated. Our parameterization of the CVD-SWIN neural network architecture consisted of adding a fourth input channel containing information about both the image itself and the precompensated color blindness direction. We tested the parameterized architecture in three training scenarios: for precompensation of protanopia and deuteranopia; for precompensation of protanopia, deuteranopia, and tritanopia; for precompensation of all color blindness directions. The experiments showed that parameterized neural networks better preserve the naturalness of colors compared to non-parameterized ones with the same size of the training dataset. Proposed P-CVD-SWIN architecture was included in OLIMP framework (Open Library for IMage Precompensation, .

• 1.    Materials and methods

All the experiments were performed using the OLIMP framework (Open Library for IMage Precompensation, .

The model used as a baseline was Generator_transformer_pathch4_844_48_3_nouplayer_server5 [18], selected by default in the authors' source code. This source code was integrated into the OLIMP framework.

In all the experiments, we used the Adam optimizer with a learning rate of 0.0002. The batch size was 4. The maximum number of epochs was limited to 50. The model with the best value of the loss function during the validation was selected as the optimal model.

• 1.1.    Loss function

All the models were trained using the same loss function, which was proposed by the authors of CVD-SWIN [18] with the coefficient a = 0.5 ensuring equal contributions of the parts responsible for chromatic naturalness and contrast:

L = (1 - a)(L[ + Lg) + a.Lni

where L , is the part of the loss function describing the local contrast; L g is the part of the loss function describing the global contrast; L_n is the part of the loss function describing the color naturalness.

The local contrast loss, L;, is calculated as follows:

L = Z ? ₌₁ X y _{£M x}

CL(x,y)

\\^x\\ ’

CL(x,y) = l\\c'x-c'y||1- \\Cx-Cy\\i|, c'x = CVD(c'x), ? y = CVD(c'y), where CL(x,y) is the contrast loss between two points, x and y; cx, cy, c'x, c'y are the colors of pixels x and y in the input and the output image, respectively; CVD(-) is the CVD retinal color simulation; \\ ■ \\1 is the L1 vector norm; wx is a set of pixels in a window of 11x11 pixels centered at x; \\wx\\ is the number of pixels in 0)x; N is the number of pixels in the image (being the same for the input and the output image).

The global contrast loss, L g , is computed using the local contrast loss between randomly selected pairs of pixels, x and y:

Lg    \\^\\Eew CL(x, y), where ш is a set of randomly chosen pairs of pixels, and \\ш\\ is the number of selected pairs, taken in the study equal to 3000, as in work [17].

To take into account the difference in the naturalness of the output and the input image, an SSIM-based loss is used:

L_n = 1 - SSIM.                                                                                     (5)

• 1.2.    Quality assessment

  The quality assessment was performed on the dataset "Collection of images utilized to assess daltonization methods and subjective evaluation results" available via the link: https://zenodo.org/records/14170170 . Dataset was proposed in the state-of-the-art article [12] and consisting of 10 real-world images. For quantitative assessment, two metrics were used: the first was to assess the preservation of naturalness and the second was to assess the preservation of contrast. Additionally, a subjective qualitative assessment was performed on the resulting images.

• 1.2.1.    Preservation of naturalness

For quantitative assessment of preservation of naturalness, the chromatic difference metric (CD) was used. CD was presented in several papers, including [22-27], and was modified from the color difference metric by ignoring changes in brightness [27]. Authors of original CVD-SWIN network [18] also used this modified CD metric for quality assessment.

CD (uref, utest) = 1. V\ ^^-a'^^^                                       (6)

where N is the total number of pixels, u_re f is the reference image, u_test is the test image, and a_test, a_re f , b_test, b_re f are the CIELAB or proLab [28] chromaticity coordinates of the test and the reference image, respectively. In our work, we used both CD metrics, in the CIELAB and proLab chromatic coordinates, as it was proposed in paper [12].

Two assessments of the preservation of naturalness will be considered: preservation of naturalness for dichromats (CD CVD) and preservation of naturalness for trichromats (CD NCV). In the first case, CD is calculated between the retinal images simulated from the original and precompensated images. The second case requires no retinal image simulation. The smaller the value of each CD metric, the better.

• 1.2.2.    Preservation of contrast

The RMS (root mean square) metric is widely used to assess contrast preservation of daltonization methods [23, 25, 28].

i  1^ 7^-^^F^^

R^MS(u ref , ^u test ) = । j | ^ ie/ J | ₀ . | ^ je0 i ^             ₁₆₀              J                                                 ⁽⁷⁾

where u_re f and u_test correspond to the original and resulting images in CIELAB coordinates, u^ and u l^est are the corresponding values in the i-th pixel, I is the set of pixels under consideration, 0 / is the set of neighboring pixels for the i -th pixel within I , | ■ | denotes the cardinality of a set, and || ■ ||₂ denotes the Euclidean norm. According to Machado and Oliveira [29], “The constant 160 in the denominator keeps the resulting value in the [0, 1] range.”

To assess contrast preservation, the RMS metric is calculated between the original image and the retinal image of the result of the method inder study. The lower the value of the RMS metric, the better.

Total color contrast (TCC) used in [18] was used as second metric for contrast preservation assessment. TCC estimated as combination of global contrast and local contrast. The lower the value of the TCC metric, the better. As in [18] number of global points for TCC was selected as 20 000.

TCC = L_g + L i (8)

• 1.3.    Training dataset

The approach proposed by the authors of the CVD-SWIN architecture [18] assumes (as in the paper [17]) training various neural network models for precompensation of protanopia and deuteranopia, and tritanopia is not considered in the paper at all. They developed special training datasets that differ for different types of dichromacy (protanopia and deuteranopia). One quarter of these datasets consists of real-world images, selected to contain color pairs confusing to people with chosen type of CVD. Other three quarters of the images in the datasets are synthesized artificially by putting specially selected (confusing to people with chosen type of CVD) color pairs on a canvas.

This creates a serious limitation on the generalization of the approach: to train a model for precompensation of tritanopia, it would be necessary to prepare another dataset. However, our studies showed that the selected dataset has little effect on the training result.

We randomly selected 10,000 images from each of datasets and trained four models (Table 1). CVD-SWIN-protan and CVD-SWIN-deutan are models trained on protanopia and deuteranopia datasets to compensate for protanopia and deuteranopia, respectively (i.e., on specialized datasets). CVD-SWIN-cross-protan and CVD-SWIN-cross-deutan are models to compensate for protanopia and deuteranopia, but trained on deuteranopia and protanopia datasets, respectively (i.e., on a non-specialized dataset). For the protanopia case, all CD metrics showed approximately the same values. CVD-

SWIN, trained on a non-specialized dataset, showed an advantage in RMS and TCC. In the case of the deuteranopia, CVD-SWIN trained on a specialized dataset showed the best result for RMS and TCC, but the worst for CD. Thus, we can conclude that there is no direct relationship between the quality of the model and its training on a specialized dataset.

During training, we split the selected dataset into training (80%) and validation (20%) samples.

Tab. 1. Comparison of a CVD-SWIN neural network trained on a specialized dataset (CVD-SWIN-protan and CVD-SWIN-deutan) and on a non-specialized dataset (CVD-SWIN-cross-protan and CVD-SWIN-cross-deutan). The first two rows were tested with CVD retinal color simulation for protanopia, the last two rows with CVD retinal color simulation for deuteranopia

NN	CDLab CVD	CD Lab NCV	RMS	TCC	CDpr0 Lab CVD	CDp r„Lab NCV
CVD-SWIN-protan	8,82	9,27	0,1073	0,1863	0,0937	0,1061
CVD-SWIN-cross-protan	9,04	9,56	0,0982	0,1731	0,1004	0,1130
CVD-SWIN-deutan	9,70	12,32	0,0881	0,1628	0,1027	0,1400
CVD-SWIN-cross-deutan	4,87	7,09	0,0908	0,1762	0,0538	0,0896

• 1.4.    Generalization of the Viénot simulation

Training the model for precompensation involves applying to the model output a distorting transformation that simulates the perception of a color image by a dichromat. The authors of the CVD-SWIN model used the linear simulation of Vienot [5]. In the linear simulator, the function CVD(c) is the operation of multiplying the color vector c by the simulation matrix. Geometrically, the linear simulation of the color vision of a dichromat transfers all points of the color space onto a certain plane, and the points are projected along a straight line (the so-called confusion line ) in the direction of which the dichromat does not distinguish color changes. If this direction is parallel to the selected projection plane or close to parallel, the simulation becomes unstable. Thus, no pre-selected plane is suitable for simulating dichromacy with an arbitrary confusion line direction, namely, it is not suitable for simulating dichromacy when the confusion line is close to parallel to the plane.

The confusion line in dichromats indicates the missing type of cones: L-, M-, and S-cones for protanopia, deuteranopia, and tritanopia, respectively. In LMS color space, the ends of the unit color blindness vectors parallel to confusion lines for protanopia, deuteranopia and tritanopia lie at the points (1,0,0), (0,1,0), and (0,0,1), respectively (Fig. 1). Therefore, we decided to specify the confusion line direction by the angular parameter у on a circle passing through these 3 points. For protanopia у = 0 ° , for deuteranopia у = 120 ° and for tritanopia у = 240 ° .

Viénot et al. proposed to use a projection plane passing through the "black", "white", "yellow" and "blue" vertices of a cube in the linRGB color space. This plane is equally suitable for simulating protanopia and deuteranopia, but is not suitable for simulating tritanopia. Therefore, we generalized Viénot's approach. To simulate tritanopia, we propose to consider a projection plane orthogonal to the one used by Viénot, passing through the "black" and "white" vertices of the linRGB cube. Moreover, our proposed approach allows simulating dichromacy with an arbitrary angular parameter of color blindness у. To do this, when constructing the simulation matrix, we select the plane of the two that intersects the given confusion line at a greater angle.

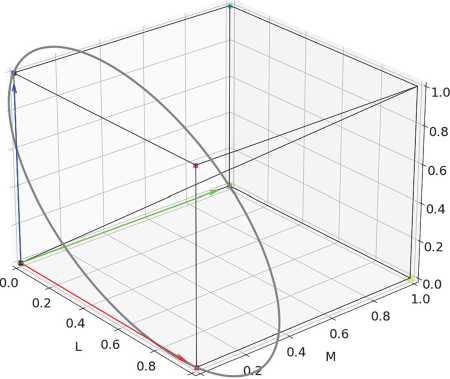
1.0 0.0

Fig. 1. Parameterization of the confusion line directions. The arrows show the color blindness vectors in LMS coordinates: protanope – red, deuteranope – green, tritanope – blue

• 1.5.    Parameterized architecture P-CVD-SWIN

• 2.    Experiments

We developed a parameterized neural network architecture P-CVD-SWIN, which receives as input not only the image requiring precompensation (as in CVD-SWIN), but also the confusion line direction. This direction is encoded in the input data as the fourth (along with R, G and B) channel of the image. Each of its pixels contains the scalar product of the unit color blindness vector (translated into linRGB coordinates) and the vector (R, G, B) of the pixel value (also in the linRGB system).

The resulting four-channel image is fed to the input of the original CVD-SWIN architecture, which supports more than 3 input channels.

The experiment compared models of the CVD-SWIN architecture trained for protanopes (CVD-SWIN-protan), deuteranopes (CVD-SWIN-deutan) and tritanopes (CVD-SWIN-tritan), with 3 parameterized models of the P-CVD-SWIN architecture:

• 1.    trained for two types of dichromacy (confusion line directions): protanopia and deuteranopia (P-CVD-SWIN-dual);

• 2.    trained for three types of dichromacy (confusion line directions): protanopia, deuteranopia and tritanopia (P-CVD-SWIN-triple);

• 3.    trained for all possible values of the angular parameter of the confusion line direction in the range [0,360) (P-CVD-SWIN-all).

Models designed for a single confusion line direction (CVD-SWIN-protan, CVD-SWIN-deutan and CVD-SWIN-tritan) were trained on a random sample from the combined dataset proposed by the authors of CVD-SWIN [18], with a size of 10,000 (large dataset) and 1,000 (small dataset) examples. The P-CVD-SWIN-dual model was trained on a random sample of 20,000 (large dataset) and 2,000 (small dataset) examples, for the first half of which the confusion line direction Y =0 ° (protanopia) was taken, and for the second half у = 120 ° (deuteranopia). The P-CVD-SWIN-triple model was trained on a random sample of 30,000 (large dataset) and 3,000 (small dataset) examples, for a third of which the confusion line direction у =0 ° (protanopia) was taken, and for the second third у = 120 ° (deuteranopia) and for the rest у = 240 ° (tritanopia).

Thus, for all the models listed, the dataset size was 10,000 (large dataset) or 1,000 (small dataset) examples for each confusion line direction the model was trained on.

The P-CVD-SWIN-all model was also trained on a random sample of 30,000 (large dataset) and 3,000 (small dataset), but uniformly distributed random values in the range [0,360) were taken as confusion line directions.

Weights for networks: CVD-SWIN-protan, CVD-SWIN-deutan, CVD-SWIN-tritan, P-CVD-SWIN-dual, P-CVD-SWIN-triple and P-CVD-SWIN-all are available for download via the folowing link:

We provided assessment of described methods for precompensation of three types of dichromacy: protanopia (Tab. 2), deuteranopia (Tab. 3) and tritanopia (Tab. 4). Each table described results for two experiments: where neural networks were trained on large datasets and on small datasets. In addition we compared our results with state-of-the-art non-NN (based on optimization) achromatic daltonization algorithm [12]. Moreover, we calculated mean values among three types of dichromacy (Tab. 5).

Tab. 2. Metric values for different methods for precompensation of protanopia-type distortions during training on large and small datasets (in case of neural network methods). Bold font – 1st best result, bold and italic – 2nd best

NN	CDLab CVD	CD Lab NCV	RMS	TCC	CDpr0 Lab CVD| CDpr0 Lab NCV
Trained on large datasets:
Achromatic dalt.	6,16	8,19	0,1206	0,2571	0,0098	0,0182
CVD-SWIN-protan	8,82	9,27	0,1073	0,1863	0,0937	0,1061
P-CVD-SWIN-dual	5,75	6,35	0,0964	0,1561	0,0673	0,0779
P-CVD-SWIN-triple	3,59	4,38	0,1076	0,1874	0,0393	0,0520
P-CVD-SWIN-all	3,06	4,58	0,1063	0,1818	0,0367	0,0576
Trained on small datasets:
Achromatic dalt	6,16	8,19	0,1206	0,2571	0,0098	0,0182
CVD-SWIN- protan	9,21	9,95	0,1187	0,2327	0,0918	0,1101
P-CVD-SWIN- dual	4,94	5,37	0,1115	0,2027	0,0513	0,0614
P-CVD-SWIN- triple	5,96	7,30	0,1060	0,1922	0,0628	0,0843
P-CVD-SWIN- all	4,66	5,66	0,1096	0,2042	0,0458	0,0667

The results showed that adding parameterization to CVD-SWIN tends to improve the preservation of chromatic naturalness, which is confirmed by subjective qualitative assessments provided in Fig. 2. At the same time, with an increase in the number of confusion line directions used in training, the preservation of naturalness improves, becoming visually indistinguishable between P-CVD-SWIN-triple and P-CVD-SWIN-all. This pattern is being violated in some cases with training on small datasets, but parametrized networks are still better than non-parametrized. In terms of contrast preservation P-CVD-SWIN-dual showed the best result, while the other neural network methods shown approximately the same results by metrics RMS and TCC (Tab. 2). In Fig. 2 P-CVD-SWIN-dual enhanced the contrast between background and the flower but at the cost on natural preservation. Original CVD-SWIN-protan network produced similar result with high contrast between background and the flower, but contrast on the flower elements was worse than in the parameterized networks.

Tab. 3. Metric values for different methods for precompensation of deuteranopia-type distortions during training on large and small datasets (in case of neural network methods). Bold font – 1st best result, bold and italic – 2nd best

NN	CDLab CVD	CD Lab NCV	RMS	TCC	CDvr0 Lab CVD | CD proLab NCV
Trained on large datasets:
Achromatic dalt.	4,60	6,40	0,0981	0,2097	0,0070	0,0132
CVD-SWIN-deutan	9,70	12,32	0,0881	0,1628	0,1027	0,1400
P-CVD-SWIN-dual	5,54	6,09	0,0757	0,1290	0,0653	0,0760
P-CVD-SWIN-triple	3,80	4,52	0,0884	0,1625	0,0431	0,0556
P-CVD-SWIN-all	2,73	4,76	0,0850	0,1564	0,0343	0,0602
Trained on small datasets:
Achromatic dalt.	4,60	6,40	0,0981	0,2097	0,0070	0,0132
CVD-SWIN-deutan	4,79	8,85	0,0972	0,1947	0,0460	0,1012
P-CVD-SWIN-dual	4,99	5,20	0,0901	0,1728	0,0530	0,0612
P-CVD-SWIN-triple	5,48	7,24	0,0805	0,1565	0,0607	0,0832
P-CVD-SWIN-all	4,04	5,30	0,0840	0,1700	0,0428	0,0641

Tab. 4. Metric values for different methods for precompensation of tritanopia-type distortions during training on large and small datasets (in case of neural network methods). P-CVD-SWIN-dual trained for precompensation protanopia and deuteranopia distortions and tested for tritanopia for comparison. Bold font – 1st best result, bold and italic – 2nd best

NN	CD Lab CVD	CD Lab NCV	RMS	TCC	CD proLab CVD	CD proLab NCV
Trained on large datasets:
Achromatic dalt.	2,94	4,86	0,0746	0,1954	0,0054	0,0090
CVD-SWIN-tritan	8,83	9,62	0,0685	0,1783	0,0859	0,0925
P-CVD-SWIN-dual	3,16	6,45	0,0632	0,1665	0,0352	0,0803
P-CVD-SWIN-triple	2,01	3,88	0,0592	0,1561	0,0221	0,0503
P-CVD-SWIN-all	3,22	4,64	0,0574	0,1565	0,0317	0,0586
Trained on small datasets:
Achromatic dalt.	2,94	4,86	0,0746	0,1954	0,0054	0,0090
CVD-SWIN-tritan	10,04	9,57	0,0655	0,1691	0,0859	0,0925
P-CVD-SWIN-dual	3,07	5,25	0,0629	0,1666	0,0318	0,0609
P-CVD-SWIN-triple	2,97	7,14	0,0614	0,1632	0,0285	0,0823
P-CVD-SWIN-all	2,91	5,47	0,0618	0,1678	0,0311	0,0656

Tab. 5. Mean metric values for different methods for precompensation of protanopia, deuteranopia and tritanopia types of distortions during training on large and small datasets (in case of neural network methods).

Bold font – 1st best result, bold and italic – 2nd best

NN	CD Lab CVD	CD Lab NCV	RMS	TCC	CDP roLab CVD	CD proLab NCV
Trained on large datasets:
Achromatic dalt.	4,56	6,48	0,0978	0,2207	0,0074	0,0135
CVD-SWIN-comb	9,11	10,40	0,0879	0,1758	0,0941	0,1128
P-CVD-SWIN-dual	4,82	6,30	0,0785	0,1505	0,0559	0,0781
P-CVD-SWIN-triple	3,13	4,26	0,0851	0,1687	0,0348	0,0526
P-CVD-SWIN-all	3,00	4,66	0,0829	0,1649	0,0342	0,0588
Trained on small datasets:
Achromatic dalt.	4,56	6,48	0,0978	0,2207	0,0074	0,0135
CVD-SWIN-comb	8,01	9,46	0,0938	0,1988	0,0746	0,1012
P-CVD-SWIN-dual	4,33	5,27	0,0881	0,1807	0,0454	0,0611
P-CVD-SWIN-triple	4,80	7,23	0,0826	0,1706	0,0507	0,0833
P-CVD-SWIN-all	3,87	5,48	0,0851	0,1807	0,0399	0,0655

P-CVD-SWIN-triple and P-CVD-SWIN-all networks (in the case with training on large datasets) are the best by metrics CD_Lab, but worse then achromatic daltonization method by C D_proLab metrics. This is not a drawback of the proposed parameterized P-CVD-SWIN architecture, but is apparently related to the loss function used for training (see section 1.1), which estimates deviations in the CIELAB space. A direction for further research could be the use of loss functions based on human color difference models [30].

Fig. 2. Example of operation of different methods for precompensation of protanopia-type distortions. The upper row is the result of the methods, the lower one is the retinal CVD simulation

Conclusion

In this paper, a modification of the CVD-SWIN neural network architecture is proposed, which allows for image daltonization for an arbitrary type of dichromacy, specified as a parameter.

We proposed to implement the parameterization of the CVD-SWIN architecture in the form of a fourth input channel, in which each pixel contains the scalar product of the corresponding pixel vector (R, G, B) of the input image and the unit color blindness vector.

For testing, we trained three neural network models of the parameterized P-CVD-SWIN architecture: a model for precompensation of protanopia and deuteranopia; a model for precompensation of protanopia, deuteranopia, and tritanopia; and a model for precompensation of all the confusion line directions allowed in our parameterization.

In the course of training and testing our neural network models, we also proposed a generalization of the Viénot simulation, which supports all the types of dichromacy, including tritanopia.

The experiments showed that parameterized neural networks better preserve chromatic naturalness, compared to nonparameterized ones having the same size of the training dataset per one confusion line direction. At the same time, the preservation of contrast does not deteriorate. It can be noted that the quality of a model increases with the number of confusion line directions for which it is trained to precompensate. This confirms our hypothesis that a neural network model trained for dichromats of one type can generalize the obtained knowledge to other types of dichromacy.

Such a parameterized neural network can also potentially be applied to take into account individual features of the spectral sensitivity in people with CVD or other factors leading to the differences in their confusion line directions from the standard ones.