Пакет обработки экспериментальных данных

ПАКЕТ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Большие трудности приходится преодолевать исследователю при оформлении результатов своих исследований, их интерпретации. Использование средств вычислительной техники (ВТ) для этой цели может существенно сократить время обработки результатов исследований, исключить субъективизм. Появление в последние годы персональных компьютеров, их доступность для исследователя, достаточно высокая вычислительная мощность, а также обеспеченность периферией дают возможность исследователю выполнять большую работу по обработке экспериментальных данных на своем рабочем месте.

В Институте физической химии основным типом ПК является ПЭВМ "Искра-226”. Этот тип компьютера хорошо подходит для решения задач обработки эксперимента (наличие периферии, графические средства отображения и выдачи).

Несколько лет назад начались разработки программ, направленных на обработку результатов экспериментов. Наибольшее распространение получила программа SIG, разработанная В. С. Ющенко, В. В. Пархаевым и Ю. В. Казакевичем. Почти двухлетняя эксплуатация этой программы выявила ее достоинства и недостатки и позволила более точно определить основные требования к подобным программам. Учитывая новые требования и недостатки старых программ, авторы разработали новый программный пакет обработки экспериментальных данных SONG.

Прототипом пакета SONG послужила программа SIG. Эта программа занимала при своей работе почти все пространство оперативной памяти ЭВМ. Однако для нужд большого числа пользователей необходимо было введение новых дополнительных функции, а дальнейшее расширение программы, в связи с ограниченным объемом памяти, было невозможно. Поэтому пришлось пойти на создание пакета оверлейных программ. Так как скорость обмена с дисковыми накопителями у ЭВМ “Искра-226" невелика (при подгрузке программ составляет всего 0.2 1.0 Кбайт в секунду), то по своей структуре пакет состоит из одного большого центрального блока и небольших по объему подгружаемых программ (утилит). Время подгрузки этих утилит колеблется от 8 до 25 с.

Как и программа SIG, пакет SONG обрабатывает однозначные функции одной переменной, заданные парами координат (х. у), до 40 функций по 51 точке. Ниже они называются "кривыми’", а термин "функция" используется для описания действий программы.

В центральный блок пакета вошли все основные функции из наиболее часто используемых в программе SIG, а именно:

I Ввод цифровых данных с клавиатуры и чтение их с диска.

• 2.    Построение графиков в декартовой системе координат Кривые могут строиться в линейных или логарифмических координатах и изображаться линиями, специальными символами или гистограммами.

• 3.    Преобразование системы координат в виде: X      = f (X        V      ) '

• 4.    Математическая обработка кривых и построение теоретических функциональных зависимостей.

• 5    Получение результатов обработки на принтере или графопостроителе.

' нов 1 v стар’ - стар у    = G (х    .у    )•

■нов 2 ' стар ^стар

Кроме того, к пакету SONG ведется разработка большого количества программ-утилит. Эти программы расширяют возможности основной программы пакета SONG. Из их числа можно отметить программы, которые производят.

построение графиков в полярной системе координат.

построение сечений семейств кривых и определение точек пересечения кривых:

• -    подбор коэффициентов математических моделей. описывающих экспериментальные данные;

визуальный ввод кривых и редактирование графического изображения:

выполнение различных штриховок кривых.

Пакет SONG ориентирован на диалоговый режим работы с широким использованием умолчаний для типичных значений параметров После запуска основной программы пакета происходит выход на меню ввода режимов работы. При этом задаются:

• -    положения системного диска с утилитами, рабочего диска с обрабатываемыми данными:

расположение и типы осей на графике: вид поля графика

Любые изменения режима работы сразу отображаются на экране. После окончания ввода режимов пользователь попадает в основное меню. Меню высвечивается в правой верхней части экрана и состоит из номеров и названии блоков Из-за большого числа функций, которые может выполнить пакет, использовано двухуровневое меню, в главном меню нажатие цифровой клавиши вызывает переход в соответствующее меню второго уровня; в меню второго уровня нажатие цифровой клавиши вызывает запуск соответствующего блока. В связи с тем что выполнение некоторых функций может занимать более нескольких секунд, пользователь должен иметь информацию о том. занята ли ЭВМ проведением каких-либо вычислений или она ожидает ввода директив. Признаком ожидания ввода директив (если на это нет специальных указаний) служит мигающий символ или мигающее сообщение в левом нижнем углу экрана. При работе в основном меню таким символом служит символ "# ", а при работе в меню второго уровня их название.

Любая интерактивная система должна учитывать человеческий фактор. Одним из таких факторов является большое число ошибок при работе (причем их осознание порой происходит "задним числом"), желание что-то изменить, не дожидаясь окончания работы. Пакет SONG позволяет прервать диалог путем нажатия клавиши СФО (нулевая клавиша пользователя). При этом происходит возврат в текущее меню программы, однако в этом случае допускается искажение изображения графика.

Для того чтобы сохранить исходные данные в случае ошибочных действий) пользователя, в пакете применен механизм дублирования кривых. Суть этого механизма заключается в следующем: пользователь может установить соответствие между любой парой кривых. При записи данных в первую кривую такой пары данные автоматически дублируются во вторую кривую пары (но не наоборот). Функции программы, которые могут привести к потере данных в случае неправильных действий (стирание кривых, преобразование координат). не затрагивают вспомогательных кривых.

Все введенные зависимости представляются на графическом экране дисплея в виде графиков в декартовых координатах (рис. 1). Причем диапазон представления как по оси X, так и по оси Y выбирается программой исходя из условий получения максимального размера графика Пользователь по своему желанию может изменить диапазон представления по любым координатам как в сторону увеличения, так и в сторону уменьшения диапазона При уменьшении диапазона, если точки зависимости попадают вне заданного диапазона, на графике они не изображаются. При построении графика программа автоматически вычисляет цену деления коор-

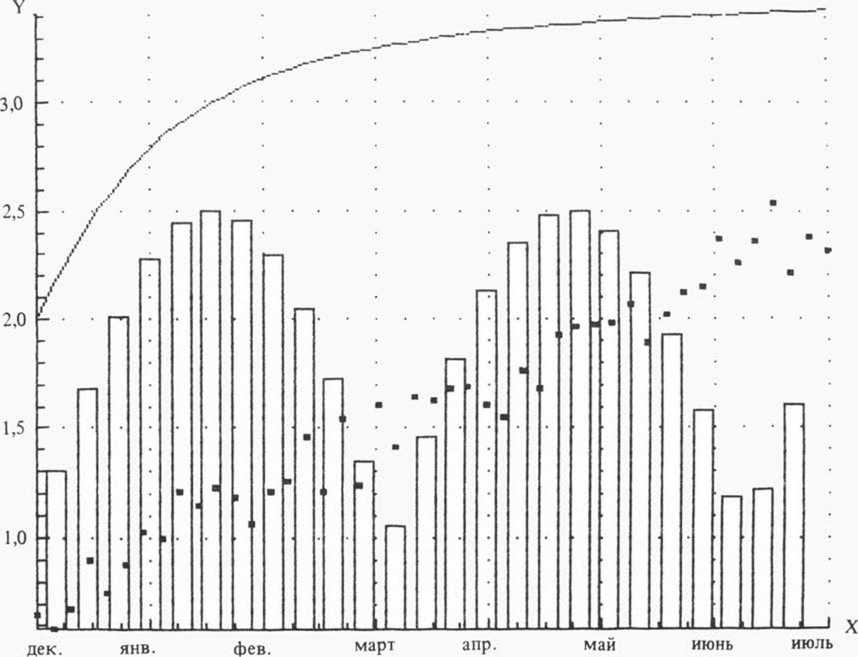
Рис. 1

динат, выделяет постоянный множитель и смещение, если это необходимо.

После изменения размеров графика дальнейшая работа осуществляется в заданных размерах, при этом график на дисплее может выйти за пределы экрана и "завернуться”, но на выводном устройстве (принтер или графопостроитель) он будет отображен правильно.

Одной из наиболее мощных и наиболее часто употребимых функций программы явилась функция преобразования кривых. Данная функция позволяет построить произвольную зависимость от значений абсциссы и любых из ранее заданных функций в данных точках, то есть

R = f(x,El (х). Е2 (х),.. . Е40(х)).

где х - независимая переменная. El, Е40 - заданные ранее функции I — 40. Значения функций в промежуточных точках находятся линейной интерполяцией. По крайним интервалам допускается линейная экстраполяция. Нужную формулу, например R = sin (х) + 10, пользователь вводит в процессе работы с программой.

Другими функциями математической обработки являются:

• -    дифференцирование. Для каждой точки выбранного участка кривой строится значение производной (дифференцированием интерполирующего полинома по трем ближайшим точкам);

• —    интегрирование. Методом трапеций строится неопределенный интеграл от заданной функции (задаваемой в явном виде или как функция от имеющихся кривых);

• —    интерполяция. Строится кубический сплайн, проходящий через все имеющиеся точки выбранного участка кривой. В узлах сопряжения полиномов непрерывны функция и две ее производные. В крайних точках вторая производная равна нулю;

• —    аппроксимация полиномом. Методом наименьших квадратов строится полином заданной степени (не выше 9). аппроксимирующий выбранный участок кривой. Дополнительно обеспечена возможность "привязки” полинома к заданной точке (в этом случае определяются коэффициенты аппроксимирующего полинома, проходящего через заданную точку). Коэффициенты полинома и среднеквадратичное отклонение точек выдаются на экран и при желании могут быть напечатаны на принтере. На рис. 2 показан пример аппроксимации экспериментальных данных полиномами 2-го, 4 и 6-го порядков.

Пакет SONG имеет большое количество утилит. Из них наиболее интересными являются функции сечений и пересечений кривых. Эта функция позволяет находить координаты точек пересечения кривых и. например, решать с помощью пакета трансцендентные уравнения самого различного вида,

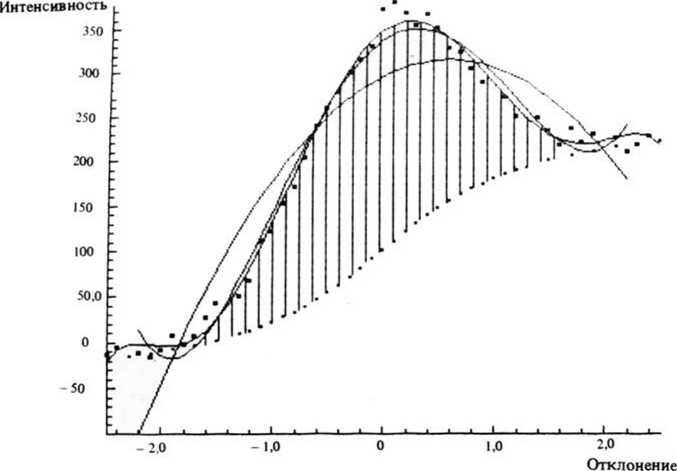
Рис. 2

строить различные сечения функций двух переменных и т. д.

Утилита приближения экспонентами позволяет найти показатели и предзкспоненциальные множители при аппроксимации кривой линейной комбинацией экспонент, что часто встречается в различных приложениях.

На рис. 2 показан пример работы программы штриховки кривых. Такая штриховка может производиться от осей координат, горизонтальных линий и между двумя кривыми. Использование штриховки позволяет выделить наиболее важные участки кривых при оформлении рисунка.

В некоторых областях техники широко используется для представления данных полярная система координат. В пакете SONG для этой цели имеется специальная утилита. На рис. 3 показан пример построения графика функции в полярной системе координат.

Система является открытой и пополняется новыми утилитами, реализующими различные функ

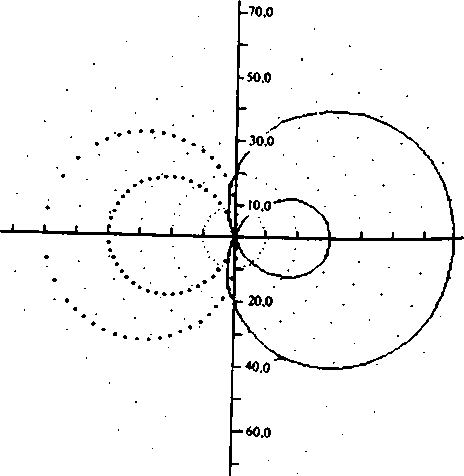
Рис.З

ции.