Параксиальное интегральное преобразование, описывающее распространение света в планарной линейно-градиентной среде

Для описания распространения световых полей в

однородных средах и различных оптических системах часто используются интегральные преобразования. Наиболее универсальными являются формулы Стреттона–Чу [1], позволяющие определять комплексную амплитуда света в любой точке, если известна комплексная амплитуда на произвольной поверхности (без токов и зарядов). Из формул Стреттона–Чу может быть получено множество других менее универсальных интегральных преобразований. Так, в однородной среде свет описывается преобразованием Рэлея–Зоммерфельда [2, 3]. Если расстояние от начальной плоскости до плоскости наблюдения много больше длины волны, то это преобразование может быть заменено преобразованием Кирхгофа [1], кото-

Позже выяснилось, что такие интегральные преобразования возникают и в градиентных средах. ABCD-преобразование описывает распространение света в градиентном волноводе с параболической зависимостью показателя преломления от поперечной координаты n ( x ) = n 0 [1 – x ²/(2 a ²)] [7–10]. В этом случае ABCD-матрица имеет вид:

A B /Г cos ( z[a ) a sin ( z/a ) C D J I - sin ( z/a )/ a cos ( z/a )

рое при параксиальном распространении света становится преобразованием Френеля [1]. Если свет распространяется не в однородной 2D среде, а через оптическую систему, описываемую ABCD-матрицей, то

при параксиальном распространении комплексные амплитуды во входной и выходной плоскостях связаны между собой ABCD-преобразованием [4]:

E (* ’z)=J2ZB

X

+да

X

+”

J E ( 5 ,0 ) exp 2B ( A У - ² * ; + D ² ) d ; .

—«

где ; и * - поперечные декартовы координаты во входной и выходной плоскостях соответственно, к = 2 л / Х - волновое число, X - длина волны света. В частности, если оптическая система – тонкая линза, то ABCD-преобразование принимает вид преобразования Фурье. ABCD-преобразование вызывало повышенный интерес в силу своей универсальности, так как могло применяться для любых систем, описываемых ABCD-матрицей. Множество работ посвящено эффективному вычислению интегралов с комплексной экспонентой, имеющей квадратичную фазу [5, 6].

где n ₀ – показатель преломления на оси волновода ( x = 0), a – показатель, характеризующий скорость спада показателя преломления от оси волновода к его краю, z – расстояние между входной и выходной плоскостью .

В [11] получено решение параксиального уравнения распространения для планарной неоднородной вдоль оптической оси градиентной среды с линейным профилем в виде преобразования Фурье от неизвестного пространственного спектра.

В данной работе на основе методологии работы [11] показано, что в 2D градиентной среде с линейной зависимостью диэлектрической проницаемости от поперечной координаты n ²( * ) = n 2 (1 -a * ) в параксиальном приближении распространение света также описывается интегральным преобразованием, ядро которого включает комплексную экспоненту, имеющую квадратичную фазу. Распространение света на расстояние z в такой среде эквивалентно прохождению через призму, сила которой пропорциональна z , последующему распространению в однородной среде с показателем преломления n 0 , повторному прохождению через упомянутую призму и дополнительному постоянному фазовому набегу, зависящему кубически от пройденного расстояния z . Показано, что при распространении гауссова пучка его центр смещается по параболе пропорционально z ², а его радиус совпадает с радиусом гауссова пучка, распространяющегося в однородной среде с по-

казателем преломления n 0 . Ускоряющийся по параболе гауссов пучок похож на пучок Эйри, ускоряющийся также по параболе в 2D однородном пространстве [12, 13]. С помощью полученного интегрального преобразования найдено явное выражение для комплексной амплитуды пучка Эйри в планарной градиентной среде с линейным профилем. Это решение совпадает с полученным ранее в [14]. Но в [14] не описан способ получения решения. Показано, что пучок Эйри при согласовании его масштаба с градиентом линейной среды, наоборот, распространяется по прямолинейной траектории.

1. Интегральное преобразование для градиентной среды с линейной зависимостью диэлектрической проницаемости от поперечной декартовой координаты

Пусть дана 2D градиентная среда с линейной зависимостью диэлектрической проницаемости (квадрата показателя преломления) от поперечной декартовой координаты:

n ² ( x ) = n 0 ( 1 -a x ) ,                                  (3)

где x – декартова координата в плоскости, перпендикулярной оптической оси z , n 0 – показатель преломления на оптической оси, a - параметр изменения диэлектрической проницаемости при удалении от оптической оси в направлениях вдоль координат x . При TE-поляризации уравнение Гельмгольца для комплексной амплитуды света Ey , распространяющегося в такой среде, имеет вид:

d² E д² E ,22/1                            а

— + —_т + к_оп ₀ ( 1 ^-a x ) E = 0,             (4)

дx    дz где к0 = 2л/Х0 - волновое число в вакууме, Х0 - длина волны света в вакууме. Будем считать, что свет распространяется преимущественно в направлении оптической оси, и представим амплитуду в виде:

E ( x , z ) = U ( x , z ) exp ( ikz ) ,                          (5)

где k = k ₀ n ₀ – волновое число на оптической оси. Тогда, пренебрегая второй производной по z , получим из уравнения Гельмгольца следующее уравнение:

2 ik— ■     - к ²a xU = 0,                    (6)

д z д x ²

решение которого будем искать в виде:

U ( x , z ) = A x

7         r ,                               (7)

x J S ( u ) exp |L i ( Bx ² + Cu ² + Dux + Ex + Fu ) J d u ,

-да где A, B, C, D, E, F – функции от z, а S – произвольная функция.

Подставим это выражение в параксиальное уравнение Гельмгольца (6), приведём подобные слагаемые и с учётом произвольности функции S ( u ), получим:

A 2 к d B + 4 B² d z

x ² -

d D

A ^{2 к}₁- ₊ 4 BD ux

A 2 к dC + D D d z

u ² -

■ A 2 к— + 4 BE + к ² a x

L d z              J

A [ ^{2 к} dF⁺² DE 1 ^{u +}

+ 2 ik — + 2 iAB - AEE d z

= 0.

Так как это выражение верно для любых равняем нулю коэффициенты при подобных

z , при-слагае-

мых. Получится система из шести обыкновенных дифференциальных уравнений первого порядка:

<

к — + 2 B ² = 0, d z

2 к — + D2 = 0, dz к — + 2 BD = 0, dz

2 к — + 4 BE + к 2a = 0, dz dF к dF + DE = 0, dz

2 ik — + 2 iAB - AE² = 0. d z

Решением первого уравнения являются функции вида:

B ( z ) =            ,

( ) 2 ( z + B 0 )

где B 0 – произвольная постоянная.

Подставив (10) в третье уравнение (9) и решив его, получим:

D ( z ) = I D T , ^{z + B} 0

где D 0 – произвольная постоянная.

Подставив (11) во второе уравнение системы (9), получим вид функций C ( z ):

C (z ) = ——0--- + C, v ! 2к^ + Bo)   0

где C ₀ – произвольная постоянная.

Подставив (10) в четвёртое уравнение системы (9) и решив его, получим вид функций E ( z ):

E(z ) = -^ E 0 ^к ^ ( z + B _o), ^V ’ z + B ₀    4 ^{V 0)}

где E ₀ – произвольная постоянная.

Подставив найденные выражения для функций D ( z ) и E ( z ) в пятое уравнение системы (9) и решив его, получим вид функций F ( z ):

F ( z    O D 0 ⁽ z + B 0 ) + ^D 0 E 0  + f ,

V !         4         k (z + B0)    0

где F 0 – произвольная постоянная.

Шестое уравнение системы (9) решается в разделяющихся переменных. Подставим найденные ранее выражения для остальных функций, получим решение:

^{A ( Z}           exP

V ^{z +} B 0

x exp

U (x, z)

_D 0 _A

2 n A °

exp [ i ( Bx ² + Ex ) ]x

+X

xj U (^,0) exp [-i (BT + E 0^)]x

-X

inx. -------7-exp

V C - C0

(Dx - D0^ + F - F0 )2 4 i (C - C0)

d ^ .

iE 0 ²

2 k (z + B0)

Подставляя в (20) функции (10)–(15), получим интегральное преобразование, связывающее комплексные амплитуды света в двух плоскостях, поперечных оптической оси:

X

x

ik ^a /        \ 3

----I Z + B +

96       0

i a E о z

.

+X

x

+X j U ^,0) exp —(^-x)

-X

2    ik a z,           ...

—(x+У dt

-

Амплитуда в начальной плоскости z =0 имеет вид:

U ( x ,0 ) = A ⁰ exp [ i ( B ⁰ x ² + E ⁰ x ) ] x

+"          г                      n             (16)

x j S ( u ) exp [ i ( C ⁰ u ² + D ⁰ ux + F ⁰ u ) J d u ,

-X где A 0 = A(0), B 0 = B(0), C 0 = C(0), D 0= D(0), E 0 = E(0), F 0= F(0).

Умножим начальное поле на множитель exp[ - iB ⁰ x ² - i ( E ⁰ + D ⁰ t ) x ] и, проинтегрировав по всей числовой оси, получим:

+X j U (x, 0) exp [-iB0x2 - i (E0 + D0t) xJ dx =

-X

+X

= A ⁰ j S ( u ) exp [ i ( C ⁰ u ² + F ⁰ u ) Jx                (17)

-X

Г +X                             1

x< j exp [ iD ⁰ ( u -t ) x J d x ^ d u .

I -X

Внутренний интеграл представляет собой дельта- функцию Дирака, и поэтому jXU (x,0) exp [-iB0x2 - i (E0 + D0t) xJ dx =

-X

= ^DA" S (^) exp [ i (C °^2 + F °^)],

т.е. функция S ( u ) выражается через начальное поле следующим образом:

S ( u ) =

D ⁰

2 n A⁰

exp [- i ( C ⁰ u ² + F ⁰ u ) Jx

+X

xj U (^,0) exp [-iBT - i (E0 + D0 u )§] d^.

-X

Подставляя (19) в (7) и интегрируя по переменной u возникающий интеграл Пуассона, получим:

Легко видеть, что при a = 0 интегральное преобразование (21) переходит в известное преобразование Френеля.

В трёхмерном случае в среде с линейной зависимостью диэлектрической проницаемости от поперечных декартовых координат n ² ( x , y ) = n 2 (1 - a x - P y ) аналогичное интегральное преобразование получается перемножением преобразований (21) по обеим координатам.

Из (21) видно, что распространение света на расстояние z в среде (3) эквивалентно прохождению через призму, сила которой пропорциональна z , последующему распространению в однородной среде с показателем преломления n ₀, повторному прохождению через упомянутую призму, и дополнительному постоянному фазовому набегу, зависящему кубически от пройденного расстояния z .

Преобразование (21) не является свёрткой, хотя и может быть вычислено с помощью преобразования Фурье. Преобразование (21) не описывает распространение света в ABCD-системе (1), но его ядро также является экспонентой с показателем в виде квадратичной формы. Следовательно известные решения для однородной среды (пучки Гаусса–Эрмита, пучки Эйри и др.) могут быть обобщены и для среды (3), а известные быстрые методы вычисления интегралов с комплексной экспонентой, имеющей квадратичную фазу [5, 6], также годятся для моделирования световых пучков в среде (3).

Заметим, что ABCD-преобразование (1) с матрицей (2) является точным решением параксиального уравнения Гельмгольца для волновода с параболическим распределением диэлектрической проницаемости. В волноводе с параболическим распределением показателя преломления распределение диэлектрической проницаемости имеет вид полинома четвёртой степени, и можно показать, что описанным способом нельзя найти решение для такой среды в виде интегрального преобразования с ядром, состоящим из экспоненты от полинома четвёртой или более высокой степени.

Если вместо линейно-градиентной среды, в которой диэлектрическая проницаемость линейно убывает в одном направлении, задан линейно-градиентный волновод, в котором она убывает в двух направлениях от оптической оси, то с каждой стороны оптической оси решение уравнения Гельмгольца может быть описано в виде (21), но с противоположными значениями параметра а . В этом случае для получения интегрального преобразования, подобного (21), требуется рассматривать граничные условия и проводить сшивку полей, расположенных по разные стороны от оптической оси. В данной работе ограничимся случаем, когда диэлектрическая проницаемость убывает в одном направлении.

2. Распространение гауссова пучка в двумерной градиентной среде с линейной зависимостью диэлектрической проницаемости от поперечной декартовой координаты

Для примера рассмотрим распространение двумерного гауссова пучка с радиусом перетяжки w :

( 2^г I

U ( ^ ,0 ) = exp l-^l .                         (22)

I w J

Тогда на расстоянии z от перетяжки пучок будет

иметь следующую комплексную амплитуду:

U ( x , z

[ w(z)

I2 exp [iZ(z)][ x

X exp ^-

[ x - x0 (z)]    ik [ x - x, (z)]w2 (z)          2 R (z)

. (23)

+ i Ф( z) •,

ф(-■ ) = — [2z■ - 3 R (z■)]-                   (29)

Из полученных выражений (23)–(29) видно, что в градиентной среде с линейной зависимостью диэлектрической проницаемости от поперечной координаты (3) при параксиальном распространении гауссова пучка его центр смещается по параболе, пропорционально z ², а его радиус совпадает с радиусом гауссова пучка, распространяющегося в однородной среде с показателем преломления n 0 .

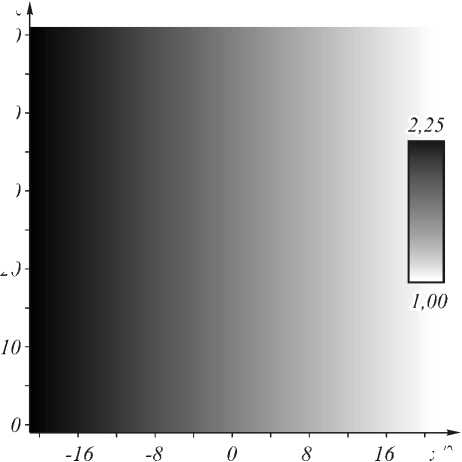
Численное моделирование распространения гауссовых пучков в среде (3) проводилось конечно-разностным FDTD-методом решения уравнений Максвелла. Рассматривалась градиентная среда с диэлектрической проницаемостью, которая в области моделирования линейно менялась от e a = 1 (воздух) до e g = 2,25 (стекло) (рис. 1). Другие параметры моделирования были выбраны следующими: длина волны света в вакууме X = 633 нм, область моделирования -20 X <  x <20 X , 0< z <50 X , время моделирования -0< t < 100 X / c ( c - скорость света в вакууме), шаг дискретизации по обеим координатам - X /16, а по времени - X /32. Диэлектрическая проницаемость в центре равна e ( x = 0) = ( e a + e g )/2 =1,625 (т.е. n ₀ =1,27). Параметр а был подобран, исходя из условий e ( x = -20 X ) = e g , e ( x = +20 X ) = e a , и поэтому a =1/52 X ^0,03 мкм^-1. Радиус перетяжки гауссова пучка составлял w = 2 X , поляризация – TE, т.е. E ≡ (0, E y , 0).

На рис. 2 а показана усреднённая по времени интенсивность в плоскости Oxz . Светлыми точками отмече-

где z R = kw ²/2 – расстояние Рэлея, w ( z ) – зависимость ширины гауссова пучка от пройденного расстояния:

2 ^z w ( z ) = w 1 + — , z _R

x ₀( z ) – зависимость координаты центра (максимума интенсивности) гауссова пучка от пройденного рас-

стояния:

^x 0 ( ^z ) =

a z ²

x 1 ( z ) – зависимость координаты центра кривизны гауссова пучка от пройденного расстояния:

ны центры гауссова пучка при различных расстояниях z , вычисленные по формуле (25). Для сравнения на рис. 2 б показана усреднённая по времени интенсивность гауссова пучка при распространении в однородной среде с показателем преломления n ₀ = 1,27. Из сравнения рис. 2 а и 2 б видно, что на одних и тех же расстояниях z радиусы гауссовых пучков совпадают, т.е. формула (24) описывает радиус пучка не только в однородной среде, но и в градиентной среде (3).

Устремим радиус перетяжки гауссова пучка к бесконечности и добавим линейный градиент фазы во входной плоскости, т.е. при z = 0 комплексная амплитуда примет вид:

U ( x , z = 0 ) = exp ( ik в x ) , (30)

x, (z) = -

x ₀

(z)-

a z R

Z ( z ) - фаза Гоу:

I z I

Z ( z ) = - arctan — ,

I zr J

где в - коэффициент, характеризующий угол наклона плоской волны. Подставляя (30) в интегральное преобразование (21), получим, что в произвольной поперечной плоскости на расстоянии z амплитуда примет вид:

U (x, z ) =

R ( z ) – зависимость радиуса кривизны волнового фронта гауссова пучка от пройденного расстояния:

,

Ф ( z ) - дополнительный фазовый набег:

= exp

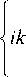
a ² z³ ав z ^{2 +} 4

(ax + в2) z

+ в x

Подобно плоской волне в однородном пространстве, поле (31) в среде (3) имеет постоянную интенсивность. Интересной особенностью (31) является кубическая зависимость фазы от пройденного расстояния z .

z/X

x/X

Рис. 1. Распределение диэлектрической проницаемости градиентной среды, линейно возрастающей от 1 (воздух, белый цвет, x = 20 2 ) до 2,25 (стекло, чёрный цвет, x = -20 2 )

3. Распространение пучка Эйри в двумерной градиентной среде с линейной зависимостью диэлектрической проницаемости от поперечной декартовой координаты

Пусть в начальной плоскости задана комплексная амплитуда пучка Эйри с ограниченной энергией [15]:

U ( x , z

I x I „I x

= 0 ) = Ai I — I exp I a— к x 0 J к x 0 .

где x0 – масштабирующий множитель, a – показатель экспоненты, ограничивающей энергию светового пучка. Подставляя (32) в интегральное преобразование (21), получим, что в произвольной поперечной плоскости на расстоянии z амплитуда примет вид:

U ( x , z ) = exp

a   k ² x 0 a ²     1 I z ³

x

^^^^^^^^^^^S   ^^^^^^^^  ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^1  ^^^^^^^»  ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^e      I ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^B

2      6     3 k ² x 0 J 4 kx 0

x exp

a I a 1

^^^^^^^^^^^^^^^^^^^^^^^™ I     ^^^^^^^^^^^™  ^^^^^^^B  ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^B

2 x ₀ V 2 k ² x 0

x exp

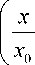
40-

30-

20-

10- zDv 50-

40-

30-

20- б)

ОА

а) z!X

50-

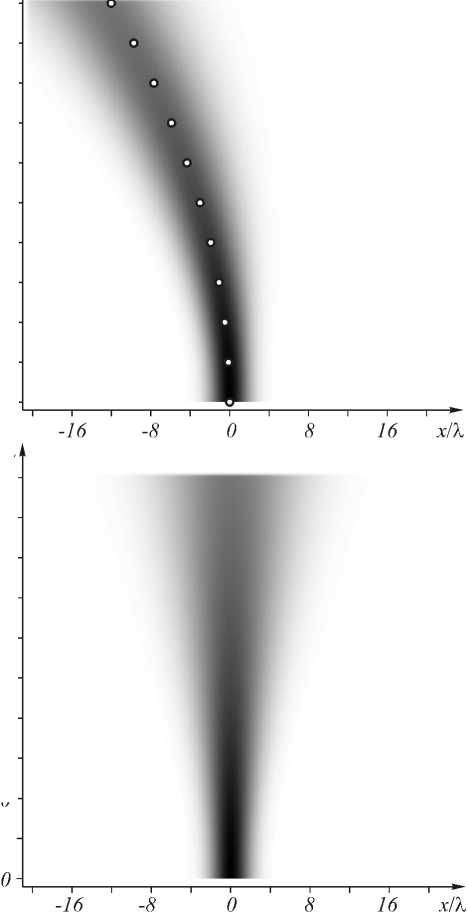
Рис. 2. Усреднённая по времени интенсивность в плоскости Oxz гауссова пучка в среде (3) (а) и в однородной среде с показателем преломления n ₀ = 1,27 (б)

22   2 zx

- k a x ₀ x + a I---2- + a I —

J 2 kx 0

x Ai

x I

--+1 a — x0

10-

1 k ² x ₀ ³

z ² iaz + 2

4 x ₀    kx ₀ ²

При переходе к пучку Эйри с неограниченной энергией ( a =0) все экспоненты в (33) становятся чисто-фазовыми, а аргумент функции Эйри – вещественным. В общем случае аргумент функции Эйри зависит от обеих декартовых координат x и z и легко видеть, что такой пучок распространяется по параболической траектории, как в однородном пространстве. Однако при согласовании параметров x ₀ и a , когда a = 1/ ( k ² x 0 ), аргумент функции Эйри теряет зависимость от z, и амплитуда (33) примет вид:

U ( x , z ) = Ai I —I . (34) V ^x 0 J

Амплитуда (34) соответствует модовому решению уравнения (4), описанному в [16, 17]. Из (34) видно, что пучки Эйри, масштаб которых согласован со свойствами среды, распространяются в линейно-градиентной среде (3) прямолинейно (рис. 3). Рис. 3 получен при моделировании FDTD-методом, параметры моделирования те же, что и на рис. 2, однако область моделирования по оси x была расширена -40 Х <  x <40 Х , поэтому параметр a был равен 1/(104 Х ), а параметр x ₀ был равен 1/( k ² a )^1/3 = (26/ n ²)^1/3 X «0,87 мкм. Небольшой изгиб траектории пучка на рис. 3 является следствием ограниченности пучка во входной плоскости.

Заключение

В работе получены следующие результаты:

1. Получено интегральное преобразование (21), описывающее параксиальное распространение светового пучка в планарной градиентной среде с линейной зависимостью диэлектрической проницаемо- сти от поперечной координаты. Показано, что распространение света на расстояние z в такой среде эквивалентно прохождению через призму, сила которой пропорциональна z, последующему распространению в однородной среде с показателем преломления n0, повторному прохождению через упомянутую призму, и дополнительному постоянному фазовому набегу, зависящему кубически от прой-

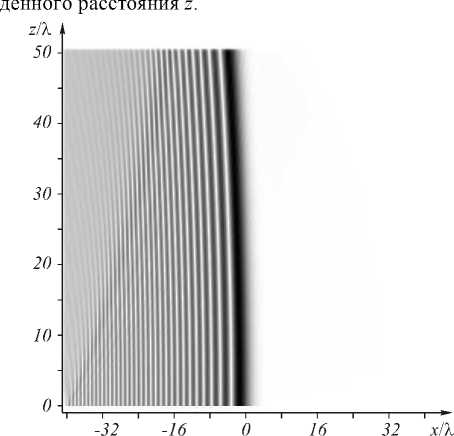
Рис. 3. Усреднённая по времени интенсивность в плоскости Oxz прямолинейного пучка Эйри в среде (3)

2. Показано, что при распространении гауссова пучка в градиентной среде (3) его центр смещается по параболе пропорционально z ², а его радиус совпадает с радиусом гауссова пучка, распространяющегося в однородной среде с показателем преломления на оптической оси среды (3).

3. C помощью полученного интегрального преобразования (21) и начального поля (32) получено явное выражение для комплексной амплитуды пучка Эйри в планарной среде с линейным профилем (33), которое совпадает с выражением, полученным в [14] другим способом.

Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации, ФЦП «Научные и научно-педагогические кадры инновационной России» (соглашение № 8027), грантов Президента РФ поддержки ведущих научных школ (НШ-4128.2012.9), молодого кандидата наук (МК-3912.2012.2) и молодого доктора наук (МД-1929.2013.2), а также грантов РФФИ (12-07-00269, 12-07-31117, 13-07-97008).