Parallel prefix sum algorithm on optoelectronic biswapped network hyper hexa-cell

Recently, the biswapped networks [4] has emerged as a better alternative to the well known OTIS networks [2], since the former has symmetrical structure and comparably larger network size (double). Actually, the biswapped network is a 2-level hierarchal and symmetrical structure that takes any graph as modules and connects them in complete bipartite manner. Thus, a large network can be constructed from its underlying modules, groups or cluster networks. The biswapped networks are Cayley (di) graphs (node-symmetrical) that supports easy embeddings and emulations. Further, efficient routing and mapping of computational algorithms are the other advantages for being a Cayley graph. The biswapped networks’ uniform structure eases selection of outgoing channel for shortest path routing (compared to OTIS networks) as it demands fewer parameter comparisons between source and the destination nodes (or processors) [4].

Although biswapped networks have such important and desirable benefits, however it contains some tradeoffs too when compared to swapped or OTIS networks. For example, increment of a single unit in the network diameter. However, its large network size lowers the overall impact of such a trade-off .

The biswapped network hyper hexa-cell [6] is a recently reported variation of biswapped networks [4] especially for mapping numerical problems where frequent routing and broadcasting (among processors) is needed. The network claims some major advantages such as, smaller diameter ; higher bisection width , higher minimum node-degree and lower network total and optical cost over its counterpart OTIS hyper hexa-cell [3] and traditional biswapped network mesh [5]. In this paper, we present parallel mapping of prefix sum problem of 2 X (6 X 2^dh-1) 2 data elements on a d_h-dimensional biswapped network hyper hex-cell (G=2N) of 2 X (6 X 2^dh-1) 2 processors (assuming each processor contain single data element). Here G and N are representing total groups (or clusters) and cluster size.

The prefix is the most commonly used numerical problem in parallel processing . It is in fact; very useful in designing fast algorithms for polynomial interpolation and generalized divide difference for hermit interpolation . It also plays a major contribution in processing numerous problems such as sorting (such as counting sort) , carry look-ahead addition , the solution of linear recurrences , scheduling problems , simulating the parallel algorithms for the Parallel Random Access Memory (PRAM) etc .

The paper is structured as follows. In Section-II, the literatures review based on the prefix sum is discussed properly. In Section-III, we analyze the computational model (biswapped network hyper hexa-cell). In Section-IV, methodology for prefix problem is presented. Further, Section-V is dedicated to the parallel algorithm for performing prefix sum over dh-dimensional biswapped network hyper hexa-cell of 2 X (6 X 2dh-1)2 data elements. Lastly in Section-VI, the suggested work is finally concluded.

III. C omputational M odel

• II.    Related Works

Basel A. Mahafzah [3] presented otis hyper hexa-cell network and performed comparison with traditional OTIS mesh. The comparison study shows that the OTIS hyper hexa-cell has advantage over OTIS mesh containing smaller diameter, higher bisection width, higher minimum node degree and lower optical cost. Wenjun Xiao [4] proposed a new class of 2-level symmetrical optoelectronic network named biswapped networks. Wei et al. [5] reported biswapped network mesh and its basic parallel algorithms. Gupta and Sarkar [6] presented recursive and symmetrical biswapped network hyper hexa-cell. The proposed network claimed advantages over OTIS hyper hexa-cell containing smaller diameter, higher bisection width, and lower network cost. In addition, this network has benefit of smaller diameter and higher minimum node degree compared to traditional biswapped network meshes. Wang and Sahni [1]

presented two parallel algorithms for N-point prefix computation on an N-processor OTIS mesh network. The first algorithm demands 8 (N 4 — 1) electronic and 2 optical moves, while second algorithm demands 7 (N 4 — 1) electronic and 2 optical moves. Jana and Sinha [7] presented improved parallel algorithm for N-point prefix computation on an N-processor OTIS mesh demands (5.5N 4 + 3) electronic and 2 OTIS moves. Mallik and Jana [8] presented prefix algorithm on mesh of trees and

OTIS mesh of trees demands 13log2 п + 0(1)electronic moves and 2 optical moves. Lukas [9] presented parallel algorithm for prefix computation on SIMD model of OTIS K-Ary 3-cube parallel computers demands O(k) electronic O(1) OTIS moves on K6 processors. Jana [10] presented improved parallel prefix algorithm on optical multi-trees requires O(logn) electronic and 4 optical moves. Jha presented [11] improved parallel prefix algorithm on n^n mesh that demands 3n + 2 moves. Jha and Jana [12] presented prefix algorithm for N2 processors multi mesh of trees needs 3.75log2 N + 6 time for N data points. Jana [13] presented prefix algorithm on N2 elements on an n×n extended multi-mesh network

takes O( N 4 ) time on N processors (13 N 4 -5 communication steps and logN + 4) arithmetic steps. Rakesh and Nitin [14] presented prefix algorithm for N data values on N processors multi mesh of trees that demands o (n^) intrablock moves. Datta, De and Sinha [15] presented prefix algorithm for N data elements on a Multi Mesh network of N processing elements demands O^N ^ )time for data communication and (logN 4 ) time for computation. Gupta and Sarkar [16] presented prefix improved prefix algorithm over n×n BSN mesh in 13(п — 1) electronic and 3 optical moves.

The present Section is dedicated to the detailed analysis of recently reported biswapped network hyper hexa-cell [6], when G=2N, where G and N represents total clusters (or groups) and cluster size respectively.

The Biswapped Network Hyper Hexa-cell (BSN HHC)

The biswapped network hyper hexa-cell [7] is a recently presented optoelectronic recursive and symmetrical optoelectronic network, where its each underlying identical cluster (d h -dimensional HHC network) is composed of 2^d h ^-1 subclusters (each subcluster is a one-dimensional hyper hexa-cell network) connected among themselves in (d_h-1)-dimensional hypercube pattern. According to the biswapped connectivity rules, every cluster in biswapped network hyper hexa-cell would be connected among themselves in complete bipartite pattern [4]. The Size of each cluster can be computed by formula: N = 6x(2^d h ^-1) [3].

Labeling of Processors

Each processor in d h -dimensional biswapped network hyper hexa-cell is labeled by subgroup and processor number, where subgroup number is represented by d h -1 bits, and processor number is represented by 3 bits. The processor numbers in each identical subcluster is labeled as 00, 01 and 10 in upper and lower triangle, starts from the top node, and then left to the right node. The left most bit for each processor (in each subgroup) is labeled as 0 for the upper triangle and 1 for the lower triangle. Further, processors of the upper triangle would be connected to their corresponding processor in lower triangle in such a way (as shown in Figures 1 and 2) that they form a subcluster (one-dimensional hyper hexa-cell network). For better understanding, the network architectures of 1, 2 and 3-dimensional hyper hexa-cell networks are shown in Figures 1, 2 and 3, respectively.

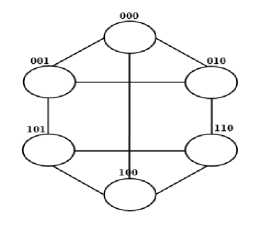
Fig.1. One-dimensional Hyper Hexa-cell Network

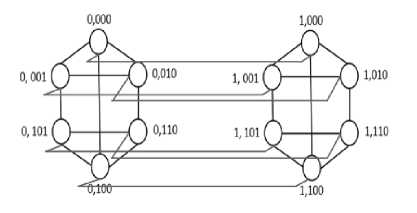
Fig.2. Two-dimensional Hyper Hexa-cell Network

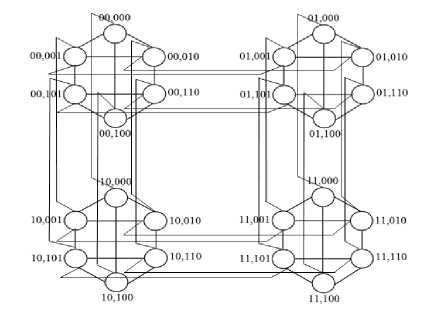
Fig.3. Three-dimensional Hyper Hexa-cell Network

Processor Connectivity: (Biswapped network hyper hexa-cell)

From architectural point of view, d_h-dimensional biswapped network hyper hexa-cell consists of 2 parts namely: part-0 and part-1. Each part contains N clusters and each cluster contains N processors. Therefore, total N² processors exist in each part, and 2N² processors in the entire biswapped network hyper hexa-cell. Basically, the biswapped networks comprises of total 2N identical clusters made of its underlying N node basis or component networks. Here N is the size of each identical cluster, where N = 6x(2^d h ^-i).

We assume P as the processor, and for routing purpose; we consider labeling of processors for each identical cluster by two parameters: c and p, where c represents cluster-id and p shows processor-id. Similarly, labeling of processors in biswapped network hyper hexa-cell contains three parameters: c, p and P’, which represents the cluster-id, processor-id, and the part-id, respectively. For better understanding, the network architectures of hyper hexa-cell and biswapped network hyper hexa-cell (G=2N) are displayed in Figures 4 and 5. In Figure 5, blue lines are representing the inter-cluster (optical) connections. In particular, we show inter-cluster connections from cluster-0 of each part only.

Inter-cluster (optical) connections:

a Vc and Vp, If cluster-id (c) does not match with the processor-id (p) , then it implies that the processor : P (c, p, 0) is connected to the processor : P (p, c, 1) and vice versa .

b Vc and Vp , If cluster-id (c) matches with the processor-id (p),  then processor: P (c, p, 0) is directly connected to the processor: P (c, p, 1) and vice versa.

/* It might be noted that no swapping is required between cluster-id and processor-id for case b*/.

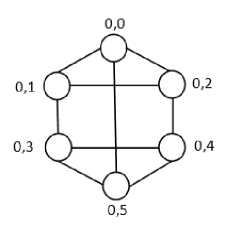
Fig.4. One-dimensional Hyper Hexa-cell Network (cluster-0)

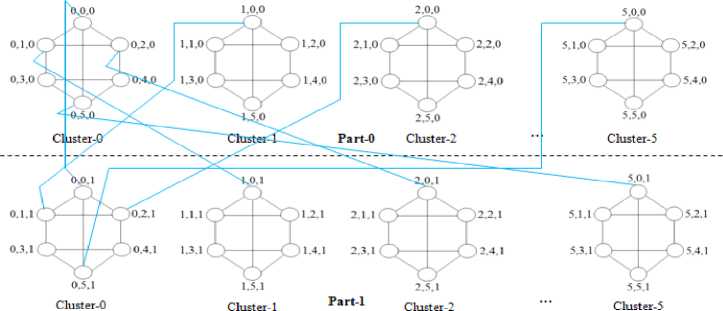
Fig.5. One-dimensional Biswapped Network Hyper Hexa-cell

• IV.    Methodology

For a given ordered set U of q elements: U = x₀, x_i, x₂ , ... ,x_q-i the resulting prefix would be the binary associative operation Ο applied as shown below in Eq. (1):

X o ,⁽X o 0X 1 ), ⁽X o 0 X i O X 2 ),..,(X o 0 X i O X 2 ,—,X_q -1 )

If the binary associative operation Ο is binary addition ⊕ , then the resulting prefix sum is as follows. (as shown in Eq. (2)).

Xo,(Xo ф Xi), (Xo ф Xi ф X2),..,(xo ф

X i фx 2 ,— ,X_q -i )                            (2)

Assume, x0 = 5, xi = 2, x2 = 8, x3 = 1 and. x4 = 7.

Then, the resulting prefix sum would be 5, 7, 15, 16 and 23.

• V.    Parallel Prefix Sum

This section is dedicated to the computation of prefix sum over d h -dimensional biswapped network hyper hexacell. We first show in subsection A, the parallel algorithm for prefix sum for one-dimensional hyper hexa-cell (subcluster). Thereafter, the parallel algorithm for prefix sum for d h -dimensional hyper hexa-cell (cluster) is presented in subsection B. Lastly, we perform prefix sum over d h -dimensional biswapped network hyper hexa-cell in subsection C. Table 1 below shows nomenclatures and their significances.

Table 1. Nomenclatures and their Significances

Nomenclature	Significance
#c	Copy data from source to destination processor.
#b	Broadcast data from source processor.
#s	Store data in destination processor.
#i	Perform inter-part move, and store the result in destination processor.
#i+	Perform binary addition via inter-part move, and store the result in destination processor.

• A.    Parallel Prefix Sum for one-dimensional hyper hexacell (subcluster)

A d h -dimensional hyper hexa-cell network (cluster) contains 2^d h ^-1 subclusters, where each subcluster contains six processors and is represented by d h -1 bits. For routing purpose, we assume labeling of each processor: P(s, p) by two parameters: s and p. The parameter: s shows subgroup number and p shows processor number, where0 < s < 2^dh-1, 0 <  p < 5.

Assume, each processor has two registers: X(s, p) and Y(s, p). Initially, registers: Y(s, p) are initialized with the data elements: x_6s+p , 0 < s < 2^d h ^-1 , 0 < p < 5 and registers: X(s, p) are initialized with the value 0.

Parallel Algorithm:

Step 1. Vs, Perform prefix computation on registers: Y(s,p) of upper and the lower triangle in parallel.

Step 2. Vs, X(s,2) #c Y(s,2).

Step 3. Vs , Broadcast data element in upper triangle from register: X(s, 2).

Step 4. Vs, Perform the steps 4.1, 4.2 and 4.3 in parallel.

4.1.  X(s,3) <#s X(s,1) Ф X(s,3). 4.2.  X(s,4) #s  X(s,2) Ф X(s,4). 4.3.  X(s,5) £ #s  X(s,0) Ф X(s,5).

Step 5. Vs and Vp, Y(s, p) ^#s X(s, p) Ф Y(s, p).

//The register: Y (s, p) yields the final result as prefix sum for one-dimensional hyper hexa-cell network. //

For better understanding, final result as prefix sum for subcuster-0 is shown in Figure 6. Here, for instance, base 0-5 representing prefix sum of six data elements ranging from 0 to 5.

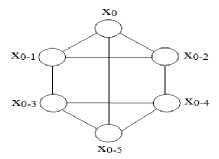
Fig.6. The Content of Registers: Y(s, p) for Subcluster 0

Time Complexity Analysis

In performing prefix sum for a one-dimensional hyper hexa-cell, Step1 demand 2 electronic moves . Further, Step 3 demands 2 electronic moves for broadcasting in the upper triangle of one-dimensional hyper hexa-cell network. Step 2, 4 and 5 need constant moves . Therefore , total 4 electronic moves are necessary to perform parallel prefix over one-dimensional hyper hexa-cell network .

• B.    Parallel Prefix Sum for dh-dimensional hyper hexacell (d_h > 1 )

The computation of prefix sum for a d h -dimensional hyper hexa-cell network requires d_h stages (d_h > 1). For example, a three-dimensional hyper hexa-cell requires 3 stages for computing parallel prefix sum.

Parallel Algorithm:

Stage1. Perform prefix computation (applying the algorithm presented in Subsection A) on each of the 2^d h ^-1 partitions in parallel, where each partition is one-dimensional hyper hexa-cell network .

Stage2. Compute prefix sum on each of the 2^d ^ ^-2 partitions in parallel, where each partition is two-dimensional hyper hexa-cell network.

/* Inter-sub cluster communication flow for the computation of prefix sum in Stage 2 of d_h-dimensional hyper hexa-cell network is displayed in Figure 7 */.

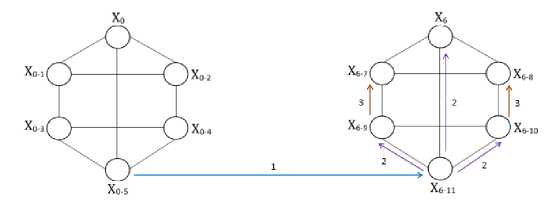
Fig.7. Inter-subcluster Communication moves for Prefix Computation in stage 2 in Dh-dimensional Hyper Hexa-cell.

Stage3. Perform prefix computation in parallel over each of the 2^d h ^-3 partitions in parallel, where each partition is three-dimensional hyper hexacell network.

/* Inter-subcluster communication flow for the computation of prefix sum of Stage 3 of d h -dimensional hyper hexa-cell network is displayed in Figure 8 */.

Stage d h . Find prefix computation over entire d h -dimensional hyper hexa-cell network .

Time Complexity Analysis

At the lowest level (Stage-1), 4 electronic steps are required for prefix computation in each partition (each partition is a one-dimensional hyper hexa-cell network) according to the algorithm for prefix computation in Subsection A. Note that, after stage-1, each stage demands dh + 1 electronic moves for computing prefix. Such as in Stage-2, parallel prefix computation over each partition (each partition is a two-dimensional hyper hexacell network) of dh-dimensional hyper hexa-cell demands 3 electronic moves. This process continues further up to stage-dh. At final stage (stage-dh),                   d^ +

1 electronic moves will be required. The total number of electronic moves required for performing parallel prefix after d h stages are shown below in Eq. (3) .

Parallel Prefix Sum = (d ^ + 1) + ((d ^ — 1) + 1) + ((d_h — 2) + 1))+.....+ 4                        (3)

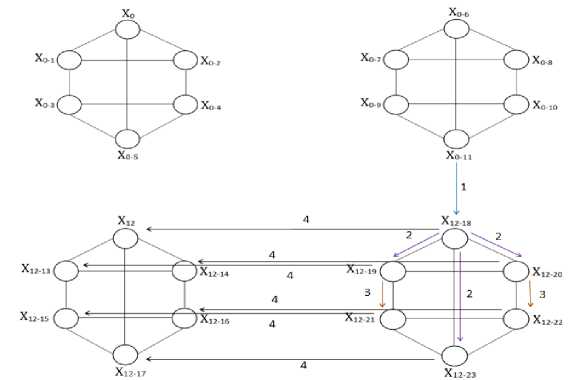
Fig.8. Inter-subcluster Communication moves for Prefix Computation in stage 3 in d h -dimensional Hyper Hexa-cell.

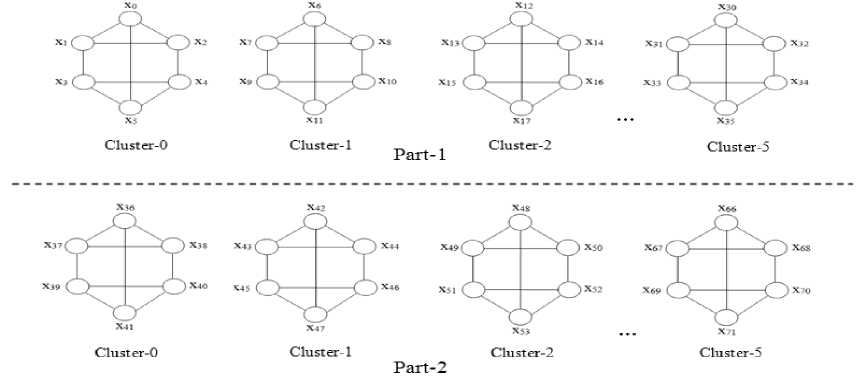
Fig.9. Initialization of Data Elements in Register: Y(c, p, P’)

Hence , the required communication moves (electronic) for prefix computation over the d h -dimensional hyper hexa-cell is as follows (as shown below in Eq. (4)).

Parallel Prefix =

((d_h — 1)(d_h + 1)) — ^(dh- ^ ²⁾ + 4      (4)

• C.    Parallel Prefix Sum for dh-dimensional Biswapped network hyper hexa-cell

Assume , each processor has three registers namely: X(c,p,P'), Y(c,p,P ' ) and Z(c,p,P') .

Vc, Vp and VP’ , registers: Y(c,p,P ' ) are initialized with the data element: X p _+cN+ p i _N 2 , and registers : Z(c,p, P ' ) are initialized with the value 0 . The initialization of Y(c,p,P ' ) registers is displayed in Figure. 9.

Parallel Algorithm:

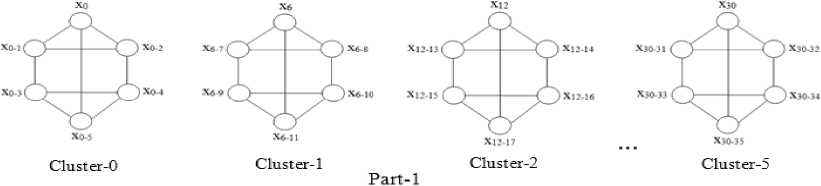
Step 1. Perform parallel prefix sum on initial data elements stored in Y(c,p,P') registers for each cluster   (dh-dimensional   hyper hexa-cell network) applying the prefix sum algorithm presented in Subsection B. For better understanding, output of prefix sum for each cluster is displayed in Figure 10.

Step 2. VP' and Vc, X(c, N-1, P^ _<#c Y(c, N -

Step 3.

Step 4.

1,    P').

Perform parallel data broadcast in each cluster.

//Call Subroutine C.1 for parallel data broadcast for each cluster// VP' and Vc , #b X(c, N-1, P ' ).

Perform the following inter-cluster moves in parallel for each of the Steps-4.1 and 4.2.

• 4.1.    Vc , Z(c + k, c, 1) ,#i   X(c, c + k, 0) , 0 <  к <

• 4.2.    Vc , Z(c + k, c, 0)   ,#i    X(c, c + K, 1), 0 < к <

(N - 1)-c.

(N - 1)-c.

//The data elements of registers: Z(c, p, P') after Step 4 is displayed in Figure 11.//

Cluster-0                     Cluster-1                   Cluster-2                      Cluster-5

Part-2

Fig.10. The data Elements as Prefix sum for each Cluster Stored in Y(c, p, P’) Registers after Step-1

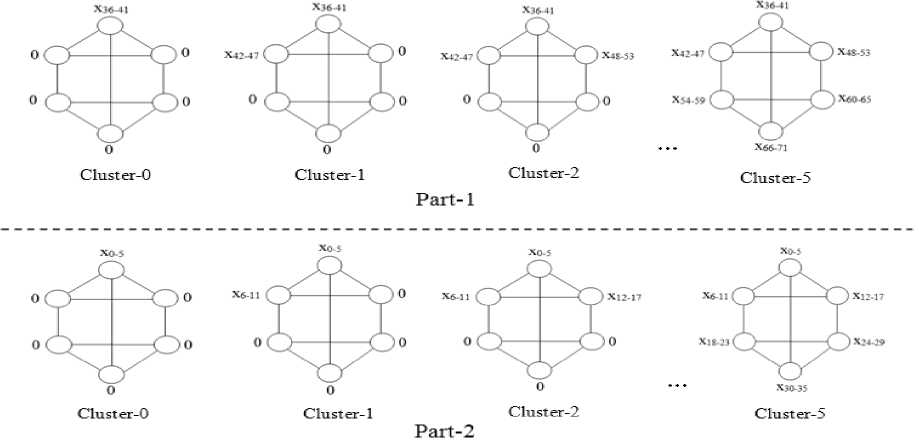
Fig.11. The data Elements Stored in Register: Z(c, p, P’) after Step-4

Step 5. VP', Perform parallel data sum on each cluster and store the result in registers: Z(N - 1, N -

• 1, P'). //Call Subroutine C.2 for parallel data

sum for each cluster//

Step 6. #b ^ Z(N - 1, N - 1, 1).

//Call Subroutine C.1 for parallel data broadcast//

Step 7. Vp, Z(p, N - 1, 0)^#i+  Z(N - 1, p, 0).

Step 8. VP' and Vc , #b Z(c, N - 1, P').

//Call Subroutine C.1 for parallel data broadcast//

Step 9. Perform the following inter-cluster moves in parallel for each of the Steps-9.1 and 9.2, where c

• 9.1.   Vc, X(c + 1, c, 1) #i Z(c, c + 1, 0), c

• 9.2.  Vc, X(c + 1, c, 0V #iZ(c, c + 1, 1), c
• Step 10. VP' and Vc, #b x, X(c, c - 1, P'), 0//Call Subroutine C.1 for parallel data broadcast//

Step 11. VP' , Vc and Vp, Y (c, p, P')    #s X (c,

• p, P'^ Ф Y (c, p, P") , where symbol Ф ,

represents binary summation.

Note: VP’ , Vc and Vp , the final result emerges from register : Y(c, p, P") . The data values stored in register: Y(c, p, P'} is displayed in Figure 12.

Time Complexity Analysis

In Step-1, ((d_h- 1)(d_h + 1))- C^ h Z12(^ h Z^ + 4 electronic moves are required to perform parallel for d h -dimensional hyper hexa-cell. Step-3 demands d_h+1 intracluster (electronic) moves for parallel data broadcast in each cluster. Steps-4, 7 and 9 needs single inter-cluster move (optical) each. Further, Step-5 demands d h +2 electronic moves for performing parallel data sum in each cluster. Step-6 again requires d h +1 electronic moves for performing the parallel broadcast in cluster-(N-1) of part-1.

Further, Steps-8 and 10 needs d h +1 electronic moves to perform parallel broadcasting of data in each cluster of both parts. Step-2 and 12 requires constant moves. Therefore, total ((d_h - 1)(d_h + 1)) - ^(dh 1⁾⁽^^h 2) + 5d h + 10 intra-cluster (electronic) and 3 inter-cluster (optical) moves are necessary to perform parallel prefix over d_h-dimensional biswapped network hyper hexa-cell.

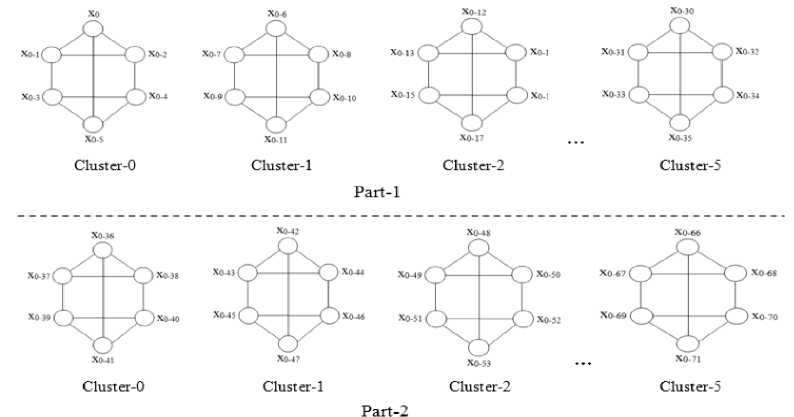
Fig.12. The data Elements Stored in Register: Y(c, p, P’) after Step-11

Subroutine C.1:

Parallel Data Broadcast on dh-dimensional hyper hexacell (cluster)

Parallel Algorithm:

Step 1. Perform parallel broadcast of data element (that need to be broadcast) in source subcluster.

Step 2. Broadcast in the entire cluster the identical copies of data elements obtained at processors of source subcluster (in Step1).

Time Complexity Analysis

In Step 1, parallel data broadcast in source processors’ subcluster needs 2 electronic communication moves (as shown by flow of data by arrows in Figure 13). In Step 2, dh-1 electronic communication moves will be required to broadcast the identical copies of data element obtained at each processor of source processors’ subcluster (as shown by flow of data blue arrows in step-3 in Figure 14). Let us assume, Processor: [0,100]) as source processor in two-dimensional hyper hexa-cell network. Figure 14 show the flow of data from source processor (Processor: [0,100]) in two-dimensional hyper hexa-cell network. Therefore, total dh+1 electronic communication moves will be required (as shown in Eq. (4)) for data broadcast in dh-dimensional hyper hexa-cell network (cluster).

Parallel Data Broadcast = d_h + 1        (4)

Fig.14. Parallel Data Broadcast (Two-dimensional HHC network)

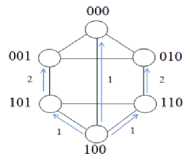
Fig.13. Parallel Data Broadcast (One-dimensional HHC network)

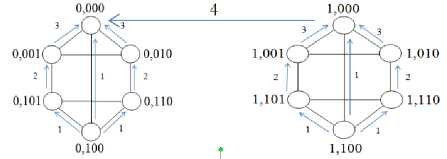
Fig.16. Parallel Data Summation (Two-dimensional HHC network)

Subroutine C.2:

Parallel Data Sum on dh-dimensional hyper hexa-cell (cluster)

Parallel Algorithm:

Step 1. Perform parallel summation of data elements in each subcluster (one-dimensional HHC network) scattered at different processors and store their outcomes at particular processors.

Step 2. Perform data communication to collect partial results (as data sum) at source subcluster from other subclusters.

Time Complexity Analysis

In Step 1, parallel data summation of data elements in a subcluster demands 3 electronic moves (as shown by flow of data by blue arrows in Figure 15). Here we assume top processor of the upper triangle to store the outcome of data sum in subcluster. In Step 2, parallel data summation in a cluster demands d h -1 electronic moves to collect partial results (data sum obtained in each subcluster). The blue arrow in step-4 in Figure 16 indicates the flow of data to collect the partial results (as data sum) obtained at each one-dimensional hyper hexacell network (subcluster) of two-dimensional HHC network (cluster). Therefore, total d_h+2 electronic moves will be required (as shown in Eq. (5) to perform parallel data summation over d h -dimensional hyper hexa-cell network (cluster).

Parallel Data Summation = d ^ + 2      (5)

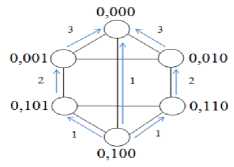
Fig.15. Parallel Data Summation (One-dimensional HHC Network) (Cluster-0)

• VI. Conclusion

In this paper, we have presented a novel parallel approach for mapping an important numerical problem of prefix sum on recently presented biswapped network hyper hexa-cell network [6] (a variation of biswapped network [4]). This algorithm mapped for 2 X (6 X 2^d h ^-1) data elements on d_h-dimensional biswapped network hyper hex-cell of 2 X (6 X 2^d h ^-1)² processors. It     demands     total    ((d ^ — 1) X (d ^ + 1)) —

——1)X^{(dh 2)} + 5d_h + 10 intra-cluster (electronic) and 3 inter-cluster (optical) moves.