Параллельные алгоритмы метода циклической прогонки

Математическое моделирование находит все большее применение в различных отраслях науки. Это связано как с развитием математического аппарата в соответствующих отраслях, так и с совершенствованием вычислительной техники. В свою очередь, новые модели и вычислительные ресурсы нуждаются в новых алгоритмах, среди которых наиболее популярными в настоящее время следует признать параллельные.

В частности, многие задачи математической физики с помощью разностного и проекционного методов сводятся к набору сеточных уравнений, записывающихся для многомерных областей в виде совокупности систем линейных алгебраических уравнений (СЛАУ) ленточного вида. При этом круговые, сферические и цилиндрические подобласти характеризуются матрицей СЛАУ, содержащей, кроме ленты на центральных диагоналях, ненулевые элементы в верхнем правом и нижнем левом углах. Для решения таких СЛАУ традиционно применяется метод циклической прогонки [1] (различные итерационные методы остаются за рамками настоящей работы).

Задавшись целью синтезировать параллельные алгоритмы этого метода, авторы обратились к параллельным алгоритмам решения ленточных СЛАУ без ненулевых элементов вне ленты, как к примерам решения аналогичной задачи. Из алгоритмов, основанных на декомпозиции области [2], циклической редукции [3] и функциональной декомпозиции [4,5], наиболее эффективными [3] были признаны последние. Их развитию для метода циклической прогонки и посвящена настоящая работа.

1. Параллельный алгоритм для одномерной сеточной области

Иллюстрируя основные идей работы рассмотрим параллельный алгоритм для одномерной области, основанный на применении встречных циклических прогонок. Не обладая свойством масштабируемости [6] он полезен при составлении алгоритмов для многомерных областей.

Функциональная декомпозиция метода циклической прогонки задается спецификой использования в ней метода обычных встречных прогонок [1].

Произведем разбиение одномерной области данных ω ¹ на равные подобласти ω ¹ ₁ и ω ¹ ₂ между двумя

задачами параллельного алгоритма. Пусть первая задача вычисляет прогоночные коэффициенты α _i , β _i, γ i и u i при 1 ≤ i ≤ g , вторая ζ i , η i , ψ i и v i при g+1≤ i ≤ N , где g - номер последнего узла подобласти ω ¹ ₁ , N – номер последнего узла областей ω¹ и ω ¹ ₂ .

Вычисления по алгоритму разделим на семь шагов: прямой ход прогонок, обмен данными, обратный ход, пересылка дополнительных данных, вычисление коэффициента y ₀ [1], пересылка коэффициента и нахождение окончательного решения.

а)

б)

в)

г)

д)

е)

ж)

Задача 1

Задача 2

П, V

to.

Задача 1

®2

Задача 2

о.

Задача 1

to.

Задача 1

Уо

0),

Задача 1

со,

Задача 1

, П, V ®2

Задача 2

Ю2

Задача 2

«,

®2

Задача 2

®2

Задача 2

to,

Задача 1

®2

Задача 2

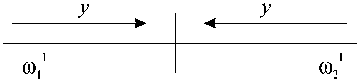
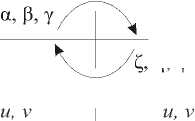
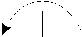
Рис. 1 Этапы вычислений по двухзадачному параллельному алгоритму, реализующему метод встречных циклических прогонок (а-в - встречный ход прогонок, г - обмен крайними коэффициентами, д - вычисление y0 , е - обмен коэффициентами, ж - вычисление окончательного решения).

Во время прямого хода (рис. 1a) прогоночные коэффициенты вычисляются одновременно с двух сторон по направлению к центру области: первая задача находит α , β, γ, вторая - ζ , η , ψ.

Обмен коэффициентами (рис. 1б) необходим для запуска обратного хода, при этом первая задача передает второй тройку коэффициентов α g+1 , β g+1 , γ g+1 , получая ζ g+1 , η g+1 , ψ g+1 .

Обратный ход прогонок (рис. 1в) реализуется обеими задачами одновременно.

На следующем шаге (рис. 1г) вторая задача пересылает в первую коэффициенты u N-1 и v N-1 [1].

Пятый шаг (рис. 1д) характеризуется вычислением y 0 первой задачей (вторая задача простаивает).

Затем полученное значение пересылается второй задаче (рис. 1е).

Вычисление окончательного решения производится обеими задачами одновременно (рис. 1ж) на последнем шаге алгоритма.

Ускорение [3] приведенного двухзадачного алгоритма оценивается величиной

_    14 Nт ар s =--------------------,

(7 N+9)т ар + 4т „ где 14Nτap – длительность вычислений по последовательному алгоритму (τap – время производства одной арифметической операции с плавающей точкой), (7N+9)τap – длительность арифметических операций для одной задачи параллельного алгоритма, τn – время пересылки одного пакета по сети. При пакетной модели передачи данных время передачи разного объема информации остается константой до тех пор, пока объем передаваемого массива не превысит размер пакета. Здесь это условие соблюдается, в дальнейшем также будем полагать его верным.

• 2.    Параллельные алгоритмы

• 2.1 Алгоритм правой циклической прогонки с линейным разбиением сеточной области

для двумерной области, основанные на методе правой циклической прогонки

В отличие от предыдущего случая, на двумерной сеточной области возможно построение параллельных алгоритмов на основе метода правой циклической прогонки, как это было предложено в [4] для ленточных СЛАУ без ненулевых элементов вне ленты.

Записывая двухзадачный алгоритм, разобьем область ω ² так (рис. 2), что вычисления циклических прогонок по столбцам области не будут требовать пересылки данных, которая останется необходимой только при работе со строками.

Первый этап вычислений по алгоритму состоит из I +1 шагов (рис. 2a-2г), где I – это число строк сеточной области. На первом шаге первая задача начинает прямой ход прогонки для первой строки (рис. 2a), вторая задача простаивает в ожидании прогоночных коэффициентов этой строки области.

Задача 1 Задача 2 Задача 1 Задача 2

1 2 а		—>	*	1 2 б
						----►
		со,2          со,2 Задача 1 Задача 2				со,2           со,2 Задача 1 Задача 2
1 2 в				1-2 г I
			--->
		--->				--->
							—►
		со,2          со,2 Задача 1 Задача 2		со/        со/ Задача 1 Задача 2
1 2 д		*	<---	1 2 е			<----
	со,2           со,2 Задача 1 Задача 2				2                  2 СО,           со. Задача 1 Задача 2
ж				з	y —►		y ч—

2                    2                            2                    2

СО,            СО,                   СО,            С02

Рис. 2 Этапы вычислений по двухзадачному параллельному алгоритму, реализующему метод правой циклической прогонки на двумерной области с линейным разбиением (а-е – начальные шаги, ж - обмен крайними коэффициентами и вычисление y₀ , з - обмен коэффициентами y ₀ и вычисление окончательного решения). Звездочками обозначены простои задач.

Второй шаг обе задачи производят одновременно (рис. 2б), осуществляя прямой ход прогонки для разных строк: вторая задача для первой, первая для второй (функциональная декомпозиция: одновременно решаются разные СЛАУ). Аналогично происходит перебор строк области вплоть да шага I , когда вторая задача производит прямой ход для строки для строки I -1, первая для I . На I +1 шаге первая задача простаивает, вторая завершает прямой ход правой циклической прогонки для последней строки области.

На втором этапе (рис. 2д, е) вычислений аналогично выполняется обратный ход прогонки для всех строк области. Теперь на первом шаге простаивает первая задача алгоритма, на последнем – вторая.

Третий этап заключается в обмене коэффициентами u и v (для каждой строки) между задачами (рис. 2ж) с последующим вычислением задачей 1 коэффициента y 0 (своего для каждой строки). Найденное значение y 0 пересылается второй задаче.

Четвертый этап – нахождение искомых сеточных функций (рис. 2з). Все вычисления независимы, простои исключены.

Обратим внимание на последнюю задачу. На первом и втором этапах она простаивает. Общая длительность простоев составляет 5Nτap, где N – размерность сеточной области по горизонтали. Длительность простоев при обратном ходе прогонки составляет 2Nτ .

ap

Простои также присущи третьему этапу при вычислении коэффициента y ₀, их длительность - 6 I τ _ap . Простои, связанные с коммуникациями характеризуются величиной (3 I +1)τ n - общим временем приема и передачи задачей коэффициентов на первом, втором, третьем и четвертом этапах.

С учетом этого ускорение двухзадачного алгоритма оценивается величиной е_            28 IN Т ap

S —---------------------------------------- .

14 IN Т ap + 6 1 Т ap + 6 N Т ap + (3 1 + 1) Т „

Распространим идею предлагаемого подхода на произвольное количество задач L с линейным разбиением сеточной области по одному направлению. На первом этапе многозадачного алгоритма в течении I + L -1 шагов производится прямой ход прогонки. На первом шаге задача 1 работает со строкой 1 (остальные задачи простаивают), на втором задача 1 работает со своей частью строки 2, задача 2 с частью строки 1 (простаивают задачи 3,.., L ). Шаг i ( L < i < I) характеризуется отсутствием простоев; причем задача l (1 < l < L ) производит прямой ход правой циклической прогонки для строки i-l+ 1 подобласти ю 2 . С шага I +1 начинают простаивать задачи с меньшими номерами.

На втором этапе вычислений аналогично выполняется обратный ход прогонки для всех строк области. Так, на шаге i ( L < i < I) задача l (1 < l < L ) производит обратный ход правой циклической прогонки для строки i-L+l подобласти ю 2 . Первые шаги этапа характеризуются простоями задач с меньшими номерами, последние – с большими.

Третий этап заключается в обмене коэффициентами u и v (каждой строки) между задачами 1 и L с последующим вычислением первой задачей коэффициента y ₀ (своего для каждой строки). Задачи 2,.., L -1 простаивают до получения y ₀.

На четвертом этапе в течении L -1 шагов производится передача вектора значений y 0 и вычисление y . На первом шаге задача 1 передает вектор значений y 0 задаче 2 и начинает вычисление y . На втором шаге задача 2 передает вектор значений y ₀ задаче 3 и начинает вычисление y . На шаге L -1 задача L -1 передает задаче L вектор значений y 0 и обе задачи начинают вычисление y . Для данного алгоритма характерна топология коммуникаций – кольцо.

Изучая длительность простоев L – задачного алгоритма, обратим внимание на последнюю задачу. На первом этапе она простаивает первые L -1 шагов, после которых работает без остановок. Длительность этих шагов составляет

L - 1

• ⁸ N L ^т ap ^{+ ( L} - ^{2 )т} n ,

где N – размерность сеточной области по горизонтали; ( L - 2) τ n – время пересылок, в которых последняя задача не принимает участия; 8 N τ _ap - длительность прямого хода прогонки.

На втором этапе задача L простаивает заключительные L - 1 шагов. Время этого простоя:

L - 1

• ⁴ N — ^Т ap ^{+ ( L} - 2^)т n ,

где 4 N τ ap - длительность обратного хода прогонки.

На четвертом этапе задача L простаивает первые L - 2 шагов. Время этого простоя:

( L - 2) τ n .

Простои также присущи третьему этапу при вычислении коэффициента y ₀, их длительность – 6 I τ _ap . С учетом этого ускорение L - задачного алгоритма оценивается величиной

. ₌_____________________ 28 IN т ap _____________________

Т.-А                         ,       .     ^,

~ Т ap + 61Т ap +12 N~г ap + 3( L - 2)Т n +(31+1)Т n где (3I+1)τn – общее время приема и передачи задачей коэффициентов на первом, втором, третьем и четвертом этапах.

• 2.2 Алгоритм правой циклической прогонки с циклическим разбиением сеточной области Стремясь избежать простоев, циклически разобьем ω² на блоки в шахматном порядке (рис. 3), ведя далее их нумерацию по блочным строкам и столбцам. Пусть задаче 1 принадлежат блоки на главной диагонали блочной области, задаче 2 - блоки, циклически смещенные на одну позицию влево от главной диагонали, задаче L - циклически смещенные на L -1 позицию влево.

1      2      3     4            L

to,2	1 toL	mJ	toL2	■ ■ ■	2 to2
(022	co,2	2 (07	«1Д	...	to/
to32	2 co2	2 0)!	2 ®L	...	2 0)4
to42	co32	to22	2 to.	...	(O52
...	...	■..	...	...	■ ■.
2 toL	2 ®Z-1	®L-2	toL-3	...	2 to.

Рис. 3 Разбиение двумерной области в случае

L–задачного алгоритма правой циклической прогонки

Двухзадачный вариант алгоритма характеризуется циклическим разбиением, представленным на рис. 4. На первом этапе такого алгоритма первая задача производит прямой ход прогонки для всех строк блока

• (1,1),    вторая задача для (2, 1). На втором шаге она работает с блоком (1, 2) (предварительно получив необходимые прогоночные коэффициенты от другой задачи), вторая задача закончит прямой ход прогонки для второй блочной строки (блок (2, 2)).

1 2

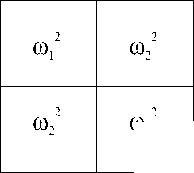
Рис. 4. Разбиение двумерной области в случае двухзадачного алгоритма правой циклической прогонки

Обратный ход прогонки (второй этап) задачи проведут с теми же блоками в обратной последовательности: первая задача начнет с (2,2), завершит с (1,1); вторая начнет с (1,2), завершит с (2,1).

Третий этап вычислений характеризуется обменом коэффициентами и и v между задачами 1 и 2 с последующим вычислением коэффициентов у ₀. А именно: первая задача получает из второй для блока (1,2) крайние значения u и v , вторая из первой - для блока (2,2) крайние значения и и v . Затем в каждой задаче вычисляется y 0 .

Четвертый этап алгоритма. Первая задача производит вычисление y для всех строк блока (1, 1), вторая задача для (2, 1). На втором шаге она работает с блоком (1, 2) (предварительно получив вектор коэффициентов y ₀ от задачи 2), вторая задача с блоком (2, 2) (предварительно получив вектор коэффициентов y ₀ от задачи 1).

Циклическая прогонка по блочным столбцам выполняется аналогично.

Исследуя длительность пересылок, найдем 6т n как общее время пересылок на первом, втором и четвертом этапах (по строкам и столбцам), 2т n -время пересылки коэффициента y 0 .

Ускорение алгоритма е_   28 IN т ap

S —--------------- .

• 14 IN Т ap + 8 т n

Идея циклического разбиения легко обобщается на случай L задач. На первом этапе алгоритма (прямой ход по блочным строкам) задача l (1 < l < L ) начинает вычисления с блока ( l , 1) и продолжает их, циклически смещаясь по своей диагонали на одну блочную позицию вниз и влево. Обратный ход производится по тем же подобластям с возвращением к блоку ( l , 1) в конце второго этапа алгоритма.

Третий этап вычислений для задачи l характеризуется обменом коэффициентов и и v с задачей l-1 (первая задача обменивается с последней), последующим вычислением y0 и их пересылкой. А именно: первая задача получает из последней крайние значения и и v для блока (1,L), вторая из L-1 крайние значения и и v для блока (2,L-1). Затем в каждой за- даче вычисляется у0. Далее производится одновременное нахождение искомых сеточных функций обеими задачами алгоритма.

На следующем этапе алгоритма задача l начинает вычисления у с блока ( l , 1) и продолжает их в течении L шагов, циклически смещаясь по своей диагонали на одну блочную позицию вниз и влево, при этом пересылая вектор коэффициентов у ₀ задаче l -1 (в случае когда l =1 пересылаем задаче L ).

Для данного алгоритма характерна топология коммуникаций - кольцо.

Хотя предложенный алгоритм в отличии от предыдущего (пункт 2.1) лишен простоев, длительность пересылок возросла в два раза.

Получим 6 (L- 1 ) как общий объем пересылок на первом, втором и четвертом этапах (по строкам и столбцам), 2т n - время пересылки коэффициента у ₀. Учитывая, что пересылки пакетные, найдем ускорение равным:

S —

28 INт_пп ap

28 IN

L ^Т ap

^{+ 6} ( ^L - ^{1 )т} n ^{+ 2 т} n

е

а

б

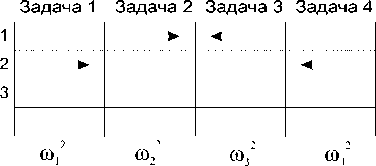
в

г

д

Задача 1 Задача 2 Задача 3 Задача 4

	*	*

2                  2                  2                  2

СО, (О, СО, С04

Задача 1 Задача 2 Задача 3 Задача 4

ж

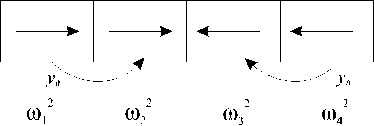
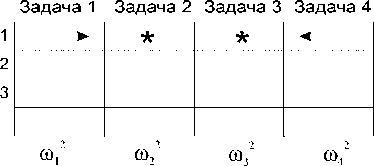
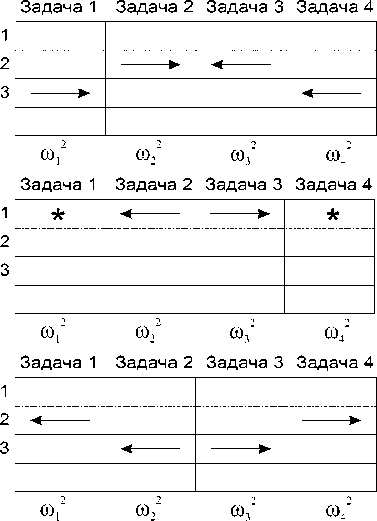
Рис. 5. Этапы вычислений по четырехзадачному параллельному алгоритму, реализующему метод встречных циклических прогонок на двумерной области с линейным разбиением (а-д - начальные шаги алгоритма, е - обмен крайними коэффициентами и вычисление y ₀ , ж - обмен коэффициентами y ₀ и вычисление окончательного решения). Звездочками обозначены простои задач

Третий этап алгоритма связан с обменом коэффициентами u и v между первой и четвертой задачами (рис. 5е) и последующим вычислением первой и четвертой задачей коэффициента y0, своего для каждой строки (при этом остальные задачи простаивают).

Четвертый этап – рассылка найденных значений y ₀ из крайних задач и вычисление значений искомых сеточных функций (рис. 5ж).

Обратим внимание на последнюю задачу. На первом и четвертом этапах она простаивает. Общая длительность простоев составляет 5 N τ ap /2

Длительность простоев при обратном ходе прогонки составляет N τ ap . Длительность вычислений на четвертом этапе N τ ap /2.

Простои также присущи третьему этапу при вычислении коэффициента y 0 , их длительность – 6 Iτ ap . (3 I +1)τ _n – общее время приема и передачи задачей коэффициентов на первом, втором, третьем и четвертом этапах. С учетом этого ускорение 4-задач-ного алгоритма оценивается величиной

28 IN Т ap

S =----

14 IN

.

^Т ap ^{+ 6} I ^Т ap ^{+ 3} N ^Т ap ⁺ ( ^{3 1 +} Ф n

Распространим идею этого подхода на четное количество задач L . На первом этапе такого алгоритма производится I + L /2-1 шагов встречных циклических прогонок. Максимальными простоями на первых шагах этапа характеризуются задачи L /2 и L /2+1, которые не участвуют в вычислениях вплоть до L /2 шага. Затем до шага I +1 простоев нет, задача l (пусть 1 < l < L /2) производит прямой ход для своей подобласти строки i - l +1 (номер шага i меняется от L /2 до I ). Аналогично проводятся рассуждения для задач L /2+1 < l < L. На заключительных L /2-1 шагах в простои вовлекаются задачи 1, L ; 2, L -1; … L /2-1, L /2+2: по паре задач за один шаг.

Вычисления по второму этапу (обратный ход встречных прогонок) выполняются в обратной последовательности шагов.

Третий этап – обмен коэффициентами u и v между первой и последней задачами, с последующим вычислением первой и последней задачей значений y 0 для каждой строки области.

На четвертом этапе в течении L /2-1 шагов производится передача вектора значений y 0 и вычисление y . На первом шаге задача 1 передает вектор значений y ₀ задаче 2, задача L задаче L -1 и начинают вычисление y . На втором шаге задача 2 передает вектор значений y 0 задаче 3, задача L -1 – задаче L -2 и начинает вычисление y . На шаге L /2-1 задача L /2-1 передает вектор значений y ₀ задаче L /2, , задача L /2+2 – задаче L /2+1 и все четыре задачи участвовавшие на этом шаге в обмене начинают вычисление y .

Для данного алгоритма характерна топология коммуникаций – кольцо.

Изучая длительность простоев, обратимся к анализу работы задачи L /2. На первом этапе она простаивает первые L /2-1 шагов, длительность которых

L — 2

⁴ N—L" ^T ap

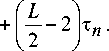
Простои исследуемой задачи на втором этапе (заключительные L /2-1 шагов) оцениваются как

L — 2

² N l ^т ap

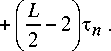
Простой на третьем этапе связан с вычислением и ожиданием приема у ₀. Длительность такого простоя составит 6 It . ap

На четвертом этапе простаивает L/2-2 шагов, длительность которых

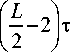
Следовательно, ускорение L-задачного алгоритма оценивается величиной s=_______________XIN_______________

28 IN    ,      l _T L — 2      Г L ^         x

Tap + 61Tap + 6N^ Tap + 3I ^ — 2 lTn + (31 + ^n где (31+1)tn - общее время приема и передачи задачей коэффициентов на первом, втором, третьем и четвертом этапах.

• 3.2 Алгоритм встречных циклических прогонок с циклическим разбиением сеточной области

Записывая восьмизадачный алгоритм, разобьем сеточную область и2 на блоки в шахматном порядке (рис. 6). В отличие от циклического разбиения, свойственного алгоритму из пункта 2.2, в данном случае сеточная область делится на четверти, дальнейшее разбиение которых происходит аналогично разбиению из пункта 2.2.

1		2	3	4
1	со,2	2 cov	2 ®8	2 со5
2	(О22	2 со,	2 со5	2 ®6
3	О)/	2 со2	2 ®6	2 со7
4	со42	2 со3	2 со7	2 ®8

Рис. 6. Циклическое разбиение двумерной области для восьмизадачного алгоритма метода встречных циклических прогонок

Вычисления по восьмизадачному алгоритму разобьем на три этапа. На первом этапе такого алгоритма первая задача производит прямой ход прогонки для всех строк блока (1, 1), вторая задача -для (2, 1), третья - для блока (3, 1) и четвертая - для (4, 1). Восьмая производит вычисления над блоком (1, 4), седьмая - над (2, 4), шестая - над (3, 4), пятая - над (4, 4). На втором шаге, задачи обмениваются коэффициентами и продолжают вычисления над следующими блоками: первая - для блока (1, 2), вто- вторая - для (2, 2), третья - для (3, 2), четвертая -для (4, 2), восьмая производит вычисления над блоком (1, 3), седьмая - над (2, 3), шестая - над (3, 3), пятая - над (4, 3). Третий шаг - это обмен коэффициентами между следующими задачами: 4 и 8, 1 и 5, 2 и 6, 3 и 7.

Обратный ход прогонки (второй этап) задачи проведут с теми же блоками, но в обратной последовательности.

Третий этап вычислений характеризуется обменом коэффициентами и и v между задачами: 4 и 8, 1 и 5, 2 и 6, 3 и 7; с последующим вычислением у ₀ для каждой строки каждого блока во всех задачах.

На четвертом этапе первая задача производит вычисление у для всех строк блока (1, 1), вторая задача -для (2, 1), третья - для блока (3, 1) и четвертая - для (4, 1). Восьмая производит вычисления над блоком (1, 4), седьмая - над (2, 4), шестая - над (3, 4), пятая - над (4, 4). На втором шаге, задачи обмениваются векторами коэффициентов у 0 и продолжают вычисления над следующими блоками, первая - для блока (1, 2), вторая -для (2,2), третья - для (3,2), четвертая - для (4,2), восьмая производит вычисления над блоком (1, 3), седьмая -над (2,3), шестая - над (3,3), пятая - над (4,3).

Исследуя коммуникации алгоритма, отметим, что 12 т_п - общее время пересылок на первом, втором и четвертом этапах (по строкам и столбцам), 2 т_п - время пересылки коэффициента у ₀.

Ускорение алгоритма

28 IN т ap

S =

7 IN т

2 ^ap

^{+ 14т} n

Идея циклического разбиения легко обобщается на случай L задач, когда log₂ L - целое число. На первом этапе алгоритма (прямой ход по блочным строкам) задача l (1 < l < L/2 ) начинает вычисления с блока ( l , 1) и продолжает их в течение L/4 шагов, цикли -чески смещаясь по своей диагонали на одну блочную позицию вниз и влево. Для задачи l ( L/2 < l < L ) вычисления начинаются с блока ( l-L/2 , L ) и продолжаются в течении L/4 шагов, циклически смещаясь по диагонали на одну блочную позицию вниз и вправо. Обратный ход производится по тем же подобластям с возвращением к блоку ( l , 1) и ( l , L ) в конце второго этапа алгоритма.

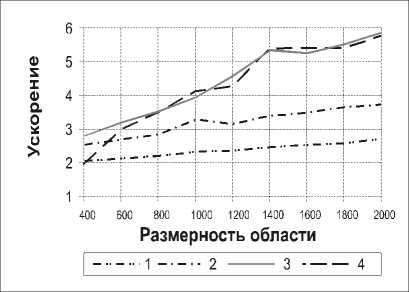
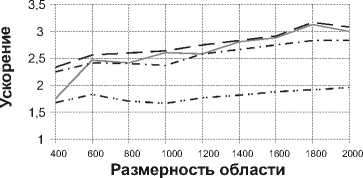
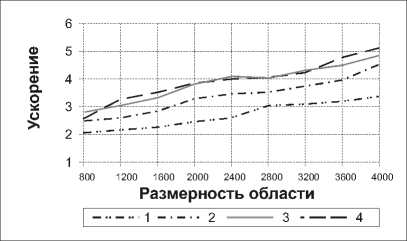
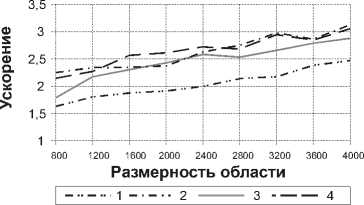
Третий этап вычислений для задачи l характеризуется обменом коэффициентов u и v с задачей l-L/2, с последующим вычислением у0. Далее производится одновременное нахождение искомых сеточных функций всеми задачами алгоритма. На этом этапе алгоритма задача l (1

Для данного алгоритма характерна топология коммуникаций - гиперкуб.

Найдем 3L/2 как общий объем пересылок на первом, втором и четвертом этапах (по строкам и столбцам), 2т_п - время пересылки коэффициента у₀.

Учитывая, что пересылки рассчитывались в рамках пакетной модели коммуникаций, получим искомое ускорение равным

S =

28 IN т ap

28 IN

------т

L ap

3 L

+--т

+ 2т

n

4. Сравнение предложенных алгоритмов

Произведем сравнение четырех подходов к записи алгоритмов для двумерной области.

Очевидно, на вытянутых прямоугольных областях (I>>N) предпочтение следует отдавать алгоритмам с одномерным (линейным) разбиением, характеризующимся в этом случае меньшим объемом пересылаемых данных, а для квадратных областей выгоднее алгоритмы с циклическим разбиением. Следовательно, уместно сравнивать алгоритмы внутри данной классификации.

Среди алгоритмов, характеризующихся одномерным разбиением, наибольшим ускорением и эффективностью обладает алгоритм, сформулированный в пункте 3.1 настоящей работы. Будучи равен по объему вычислений и количеству пересылаемых данных с алгоритмом, использующим правую прогонку (пункт 2.1), он характеризуется вдвое меньшей длительностью простоев. К недостаткам обсуждаемого алгоритма из 3.1 можно отнести наличие простоев (впрочем, не играющее существенной роли в приведенном сравнении в силу их кратковременности по сравнению с длительностью арифметических операций и коммуникаций) и требование на четность к числу процессоров вычислительной системы (также несущественное, учитывая, что современные кластеры, как правило, составляются из двухпроцессорных ЭВМ).

Проводя изучение алгоритмов с циклическим разбиением, для простоты положим I=N. Тогда алгоритм из 3.2 будет отличать от алгоритма из 2.2 вчетверо меньший объем коммуникаций. Недостатками синтезированного алгоритма из 3.2 следует признать ограничение на количество требуемых процессоров (степень двойки) и высокое требование к топологии коммуникаций вычислительной системы (гиперкуб). Однако большинство современных кластеров удовлетворяют таким требованиям.

г

Рис. 7. Результаты вычислительных экспериментов: а - для восьмизадачных алгоритмов на квадратной области, б - для четырехзадачных алгоритмов на квадратной области, в - для восьмизадачных алгоритмов на вытянутой прямоугольной области, г - для четырехзадачных алгоритмов на вытянутой прямоугольной области.

Линии на графике: 1 - параллельный алгоритм правой циклической прогонки с линейным разбиением, 2 - встречных циклических прогонок с линейным разбиением,3 - правой циклической прогонки с циклическим разбиением и 4 - встречных циклических прогонок с циклическим разбиением

б

Переходя к сравнению параллельных вычислительных процессов, порожденных представленными алгоритмами, отметим, что благодаря отсутствию простоев и меньшему объему коммуникаций (данные передаются блоками), наилучшие результаты на квадратных областях продемонстрировали алгоритмы с циклическим разбиением области. При небольшом количестве задач на сильно вытянутых прямоугольных областях, большую эффективность показывает параллельный алгоритм встречной циклической прогонки с линейным разбиением области.

Заключение

Применение функциональной декомпозиции к синтезу параллельных алгоритмов, основанных на методах правой и встречных прогонок для решения сеточных уравнений трехдиагонального вида, оправдано и приводит при указанных условиях к алгоритмам, обладающим высоким ускорением и эффективностью.

Представляется целесообразным развитие данного подхода к синтезу алгоритмов для решения ленточных систем с большим количеством диагоналей.

Работа выполнена при поддержке Российско-американской программы “Фундаментальные исследования и высшее образование” (BRHE), а также Фонда содействию отечественной науке, гранта Президента РФ (N НШ – 1007.2003.01) и гранта РФФИ (N 04-07-90149).