Параллельный метод для расчета надежности сетей с ограничением на диаметр

Введение. В процессе эксплуатации элементы сетей связи могут подвергаться отказам. Причины отказов могут быть различны, например, поломка, износ, природные явления, результат преднамеренных действий злоумышленника, и другие. Подобные сети обычно моделируются случайным графом G = (V,E) [1], вершины которого соответствуют узлам сети, а ребра — каналам связи. Для каждого элемента графа задано некоторое вещественное число p Е [0,1] — вероятность исправной работы элемента, что соответствует надежности соответствующего элемента сети.

Наиболее часто рассматривается случай, когда все узлы в сети абсолютно надежны, в то время как для каждого ребра e Е E задана вероятность отказа q e = 1 — p e. Предполагается, что отказы ребер происходят независимо. Сеть считается работоспособной, если она

Работа, поддержана. РФФИ: гранты № 13-07-00589, 14-07-31069.

связна, т. е. если ее узлы связаны друг с другом посредством исправных ребер. Надежностью сети называют вероятность соответствующего события, т. е. вероятность связности графа. Часто рассматривается выделенное множество узлов сети — терминалов (плюсов). В таком случае сеть полагается работоспособной, если каждая пара терминалов связана посредством исправных ребер. Задача расчета вероятности связности заданного подмножества узлов сети является NP-трудной [1]. Данный показатель надежности достаточно хорошо изучен, разработано большое количество различных точных и приближенных методов расчета [1-4].

Однако на практике во многих случаях требуется обеспечить не просто существование пути между каждой парой узлов, а существование пути, проходящего по ограниченному числу каналов связи [5-6]. Например, если есть ограничение на время передачи данных между двумя узлами — T, то количество транзитных узлов, участвующих в передаче данных, не должно превышать T/t, где t — требуемое время для обработки данных на каждом узле сети. Для таких случаев в [7] был введен другой показатель надежности — вероятность связности сети с ограничением на диаметр, R K (G,D). Этот показатель надежности есть вероятность того, что любые два узла из заданного множества K соединены в графе G путем длины не более d.

Как и задача расчета вероятности связности, задача расчета вероятности связности с ограничением на диаметр NP-трудна [7]. Вопрос о сложности данной задачи в зависимости от значений диаметра и количества полюсов является к настоящему моменту полностью изученным [8]. В наших прошлых работах совместно с А. С. Родионовым [9-11] были предложены различные методы структурной редукции и декомпозиции для ускорения расчета надежности сети с ограничением на диаметр.

В настоящей работе представлены и исследованы два параллельных алгоритма для вычисления точного значения надежности заданной сети с ограничением на диаметр. Один алгоритм основывается на методе факторизации [1], а второй на модификации данного метода, предложенной в [7]. Для распараллеливания использована парадигма параллельного программирования „ведущий-ведомый“, подобно тому, как это было ранее сделано для разработки параллельного алгоритма расчета надежности сети без ограничения на диаметр [4]. Проведенные численные эксперименты позволили значительно улучшить масштабируемость алгоритмов.

• 1.    Основные определения и обозначения. Будем представлять сеть с ненадежными ребрами с помощью неориентированного случайного графа G = (V,E), для каждого ребра e которого задана вероятность его присутствия в графе re. Задано выделенное множество вершин K С V — полюсов, соответствующих узлам сети, для которых необходимо обеспечить возможность устанавливать соединение друг с другом.

• 2.    Метод факторизации. Расчет R K( G,D ) непосредственно по определению приведет к перебору всех реализаций графа, что делает расчет невозможным даже при небольшой размерности. Поэтому для расчета различных показателей надежности используются другие методы, самый распространенный из которых — метод факторизации [1]. Метод заключается в рекурсивном применении формулы полной вероятности при рассмотрении в качестве альтернативных гипотез наличия либо отсутствия очередного разрешающего ребра. В общем случае формула для выбранного ребра e имеет вид

Элементарным событием будем называть частную реализацию графа, определяемую присутствием или отсутствием каждого ребра. Таким образом, общее количество элементарных событий составляет 2|E|. Вероятность элементарного события равна произведению вероятностей присутствия исправных ребер, умноженному на произведение вероятностей отсутствия отказавших ребер.

Вероятность связности графа G с ограничением на диаметр D определяется как сумма вероятностей всех частных реализаций графа, в которых любая пара вершин из множества K связана не более чем D ребрами. Далее будем называть эту характеристику надежностью графа или соответствующей сети и обозначать как R K (G, D) Под путем понимается путь без самопересечений, под длиной пути в графе — количество ребер в этом пути.

Rk ( G,D ) = r e х R k ( G \ e, D ) + (1 - r e ) x R k (G/e, D),                (1)

где G/e — граф G без ребра e, G \ e — граф G, в котором ребро e абсолютно надежно. Множества вершин V и терминалов K остаются теми же.

В [7] предложен модифицированный метод ветвления для расчета надежности сети, который работает существенно быстрее, чем вышеописанный классический метод ветвления (1) в случае с ограничением на диаметр. Далее будем обозначать этот метод как С&Р. Основная его идея состоит в переходе от графов к спискам путей P. На начальном этапе формируется список всех путей длины, не превосходящей D для каждой пары полюсов. Это автоматически исключает из рассмотрения все ребра, через которые не проходит ни один такой путь, например, так называемые „прикрепленные деревья" без полюсов. Для каждого оставшегося ребра e формируется список P (e) всех содержащих его путей. При рекурсивных вызовах процедуры в качестве параметров не передаются подграфы, вместо них передается шесть параметров, описывающих состояние соответствующего подграфа с точки зрения путей из P. Ниже приведены псевдокод этого алгоритма и описание используемых в нем вспомогательных параметров.

• 1)    np st — количество пут ей длины не более D между полюсами s ii t:

• 2)    links p — число ребер в пути p G P, не являющихся абсолютно надежными;

• 3)    feasible p — принимает значение false, если путь p включает абсолютно ненадежное ребро, true — иначе;

• 4)    connected st — принимает значение true, если вершины s и t соединены абсолютно надежным путем длины не более D, false — иначе;

• 5)    connectedPairs — число пар полюсов, связанных абсолютно надежными путями ограниченной длины.

Псевдокод алгоритма Cancela и Petingi [8].

• 1:    function FACTO( P, np _st , links p , feasible p , connected _st , connectedPairs')

• 2:    RContract ^ 0                        . случай, отвечающий стягиванию ребра

• 3:    RDelete ^ 0                            . случай, отвечающий удалению ребра

• 4:    e ^ случайное ребро : 0 < r e <  1

• 5:     for all p = (s,... ,t) G P, где feasible p = true do            . "Стягивание ребра"

• 6:        links p ^ links p — 1

• 7:        if connected st = false и links p = 0 then

• 8:            connected st ^ true

• 9:           connectedPairs ^ connectedPairs + 1

• 10:            if connectedPairs = ^kx,k ' then

• 11:              RContract ^ 1

• 12:              GoTo( "Удаление ребра")

• 13:            end if

• 14:         end if

• 15:     end for

1G:     RContract ^ FAC"TO(P, np _st , links p , feasible p , connected _st , connectedPairs)

• 17:     for all p = (s,... ,t) E P, где feasible p = true do                . "Удаление ребра"

• 18:         feasible p ^ false

• 19:         np st ^ np st - 1

• 20:        if connected st = false и links p = 0 then

• 21:            feasible p ^ false

• 22:            np st ^ np st - 1

• 23:            if np _st = 0 then

• 24:              RDelete ^ 0

• 25:             СоТо("Финальные вычисления")

• 26:            end if

• 27:         end if

• 28:     end for

• 29:     RDelete ^ FACП?О(Р, np _st , links _p , feasible p , connected _st , connectedPairs')

• 30:     R K (G,D) = r e x RContract + (1 — r e ) x RDelete . "Финальные вычисления"

• 31:     Return R K (G,D)

• 32:    end function

• 3.    Параллельный алгоритм расчета надежности сети с ограничением на диаметр. Основная идея предлагаемых параллельных алгоритмов заключается в следующем. В процессе факторизации при разбиении задачи на две новые подзадачи одна из них может передаваться для решения на свободный процесс, а вторая оставаться на исходном. Если свободных процессов нет, то обе подзадачи остаются на исходном процессе. Например, подзадача „удаления" выбранного ребра остается на текущем процессе, а подзадача „стягивания" этого ребра или отправляется на любой из простаивающих процессов, если такой есть, или остается на этом же процессе. Разница для двух модификаций метода факторизации заключается только в формате передаваемых данных.

В таком виде данный подход имеет существенные недостатки. Поскольку алгоритм основан на формуле факторизации, вычисленное в процедуре значение необходимо отправить на родительский процесс для умножения этого значения на соответствующую вероятность и суммирования. Это может приводить к дополнительным пересылкам и простою процессов. Например, первый процесс выполняет „удаление" выбрани ого ребра e, вычисляя R K (G/e^D) а на другом процессе выполняется „стягивание" для этого ребра, вычисляя R K (G \ e,D). И первый процесс должен будет ждать, пока второй процесс вычислит второе значение и перешлет его, и только после этого вычислит R K (G,D).

По аналогии с параллельным методом для расчета всетерминальной надежности без ограничения на диаметр [4] предлагается отправлять на процесс-помощник подзадачу вместе с вероятность получения этой подзадачи. Вероятность получения реализации подсети — переменная, значение которой меняется в течение процесса. Для исходной сети это 1. Например, в выражении (1) вероятность подзадачи стягивания — это re, а вероятность подзадачи стягивания равна 1 — re. При этом нужно учесть, что исходная задача тоже имеет определенную вероятность, на которую нужно умножить приведенные значения. Данный подход помогает избежать обратных посылок значений надежности, накапливая на каждом процессе свое собственное значение. В конце все эти значения суммируются на отдельном процессе и получается точное значение надежности.

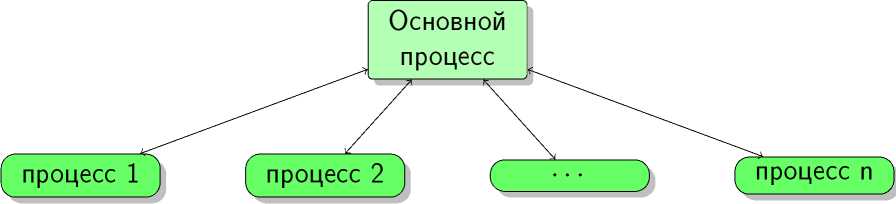
Рис. 1. Схема „ведущий — ведомый"

Для организации взаимодействия между процессами использована схема „ведущий — ведомый“ (рис. 1), в которой выделяется один „контролирующий" процесс, называемый ведущим. Этот процесс ответственен за загрузку остальных и суммирование полученных значений. Ведомый процесс получает задачи от других ведомых процессов по указанию ведущего, выполняет их, возвращает полученные результаты, и снова получает новую задачу. При необходимости ведомый процесс может попросить помощи в виде одного из простаивающих процессов для распределения работы.

Ведугций процесс:

• 1)    контролирует загруженность остальных процессов;

• 2)    отправляет исходный граф для вычисления на один из ведомых процессов;

• 3)    при получении запроса о помощи либо отказывает в ней, либо посылает номер свободного процесса;

• 4)    суммирует вычисленные на каждом процессе значения, получая итоговое значение надежности.

Ведомый процесс:

• 1)    в начале инициализируется как простаивающий;

• 2)    при получении задачи процесс выполняет процедуру (1). Одна из подзадач, например, R K (G/e, D) остается для вычислений на этом процессе, после чего происходит запрос к ведущему процессу, от которого приходит ответ либо в виде номера свободного процесса, либо с сообщением отказа (т. е. если все процессы уже заняты). Далее, в зависимости от полученного ответа, вторая подзадача вместе с соответствующей вероятностью либо отправляется на вспомогательный процесс, либо остается на исходном для дальнейших вычислений;

• 3)    после того, как все вычисления закончены, отправляет накопленные значения на ведущий процесс и ждет следующей задачи.

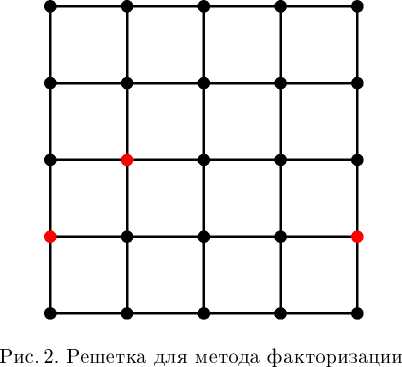
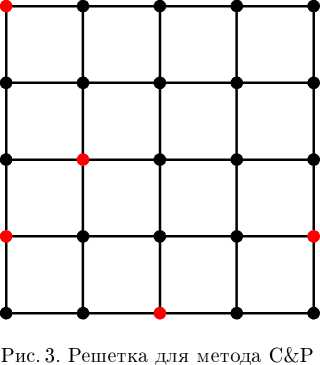
• 4.    Результаты численных экспериментов. Для сравнения масштабируемости двух параллельных алгоритмов (метод факторизации и метод С&Р) была выбрана решетка 5x5 с тремя терминалами (рис. 2-3), терминалы выделены цветом). Диаметр полагался равным 4. Значение надежности последовательным методом факторизации было вычислено за 16 мин 9,507 с, количество рекурсий было равным 249 602 055. В то же время второй алгоритм закончил работу всего за 0 мин 0,061 с с 74 рекурсиями. Поэтому для второго алгоритма были усложнены входные данные с целью сделать время исполнения обоих алгоритмов примерно одинаковым. Были выбраны следующие параметры: количество терминалов равно 5, значение диаметра равно 9. С новыми данными алгоритм С&Р закончил вычисления за 16 мин 35,169 с, количество рекурсий оказалось равным 1 154 905 688.

Как уже упоминалось, разница для двух модификаций метода факторизации заключается только в формате передаваемых данных. В модификации метода факторизации [7] работа ведется со списком структур, а не с конкретным графом. Необходимо оперировать с гораздо большим по размеру количеством информации. Пересылка подзадач от одного процессора к другому осуществляется за намного большее время, чем, в базовом методе факторизации. Но в последовательной реализации базовой метод факторизации значительно медленней, чем модифицированный [7] и дополнительно усиленный в соответствии с [11]. В следующем пункте выясняется, какой метод предпочтительней в параллельной реализации.

В работе [4] для ускорения параллельного расчета всетерминальной надежности без ограничения на диаметр был введен параметр N edges — минимальное число ребер в графе, необходимое для отправления этого графа на вспомогательный процесс. Например, для графа малой размерности быстрее посчитать надежность на одном процессе, без пересылок. Результаты численных экспериментов показали, что этот параметр существенно влияет на скорость работы алгоритма. После введения параметра N edges результаты масштабируемости изменились в лучшую сторону. На рис. 5 и 6 можно видеть, что ускорение алгоритмов заметно улучшилось для обоих алгоритмов. Поиск оптимального значения параметра N edges велся методом бинарного поиска. Видно, что итоговое значение лежит между значениями 15 и 20 (дальнейший поиск параметра бессмысленен, так как разница времени исполнения для параметров 15 и 20 отличалась лишь на одну секунду).

ВРЕМЯ РАБОТЫ (С)                                       ВРЕМЯ РАБОТЫ (с)

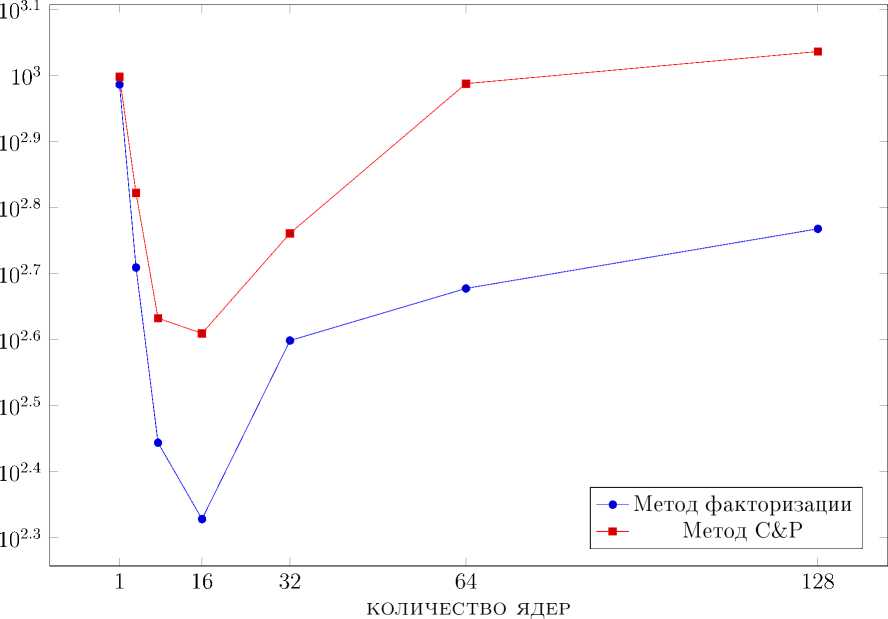
Рис. 4. Зависимость времени исполнения от количества, ядер

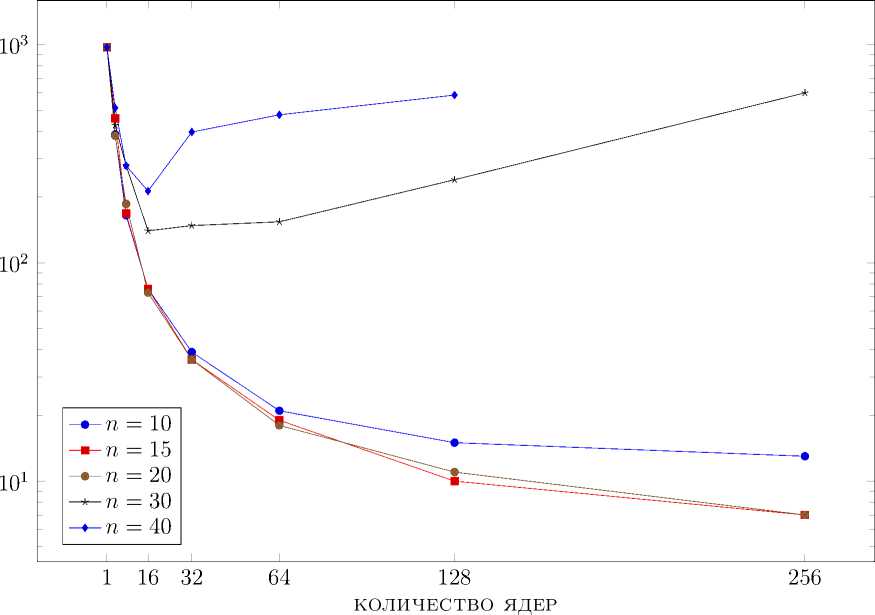
Рис. 5. Зависимость масштабируемости от параметра N edges для метода факторизации

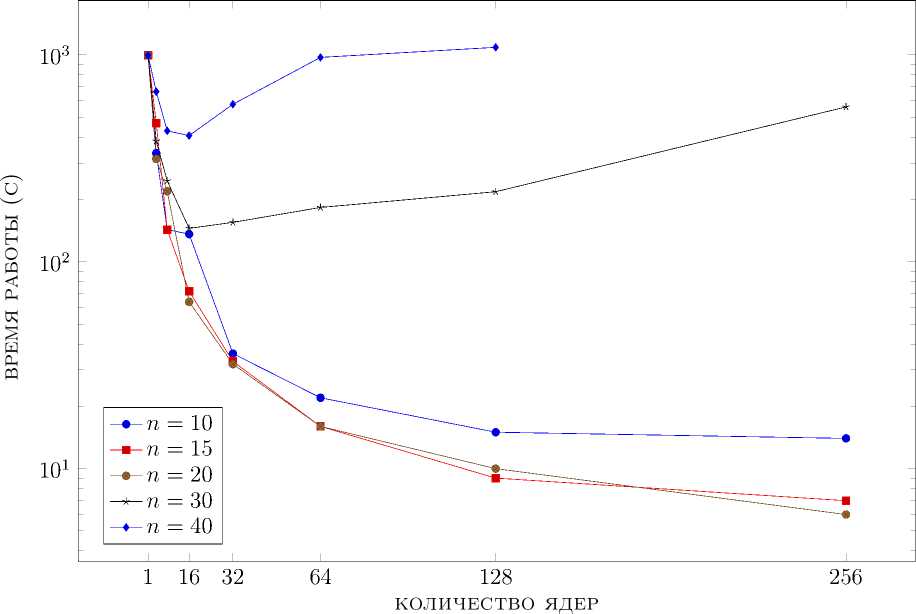
Рис. 6. Зависимость масштабируемости от параметра N edges для метода С&Р

Заключение. Для NP-трудной задачи расчета надежности сети с ограничением на диаметр предложены параллельный алгоритм, основанный на методе факторизации, и параллельный алгоритм, основанный на модификации метода факторизации С&Р. Для распараллеливания использована парадигма параллельного программирования ” ведущий — ведомый“. Численные эксперименты позволили оптимально настроить параметры алгоритмов и значительно улучшить их масштабируемость. Как и в последовательном случае, метод С&Р работает существенно быстрее в параллельной реализации, чем базовый метод факторизации.