Параметр Грюнайзена и отношение скоростей распространения продольной и поперечной акустических волн в стеклах

Параметр γ D определяется изменением частоты колебаний решетки в зависимости от изменения объема системы и обычно вычисляется по уравнению Грюнайзена из экспериментальных данных о коэффициенте объемного теплового расширения β , изотермическом модуле объемного сжатия B , молярном объеме V и молярной теплоемкости при постоянном объеме C_V

P B V

Y d =

V

Недавно на основе экспериментальных данных [1, 2] для двух групп кристаллов был обнаружен необычный факт – линейная зависимость параметра Грюнайзена γ D от отношения скоростей распространения продольной ( v L ) и поперечной ( v S ) звуковых волн [3, 4]

Y d = C

I vs J

где величина γ D определена по уравнению Грюнайзена (1), С 1 и С 2 – эмпирические постоянные.

Необычность этой формулы заключается в том, что она однозначно связывает между собой гармоническую ( v_L / v_S ) и сугубо ангармоническую ( γ_D ) величины. Между тем принято считать, что линейные и нелинейные коэффициенты в разложении потенциальной энергии решетки по деформации являются независимыми параметрами.

Настоящая работа посвящена исследованию зависимости параметра Грюнайзена от отношения скоростей звука v_L / v_S для стеклообразных твердых тел, которые можно считать фактически изотропными или по крайней мере квазиизотропными средами. Обсуждается природа взаимосвязи между параметром Грюнайзена и отношением скоростей акустических волн v L / v S , которое у изотропных веществ является однозначной функцией коэффициента Пуассона.

Линейная корреляция между γ d и v l / v s для стекол

Для некоторых классов твердых тел, особенно для стекол, не всегда удается найти необходимые данные о величинах, входящих в уравнение Грюнайзена (1). Поэтому при расчетах γ_D иногда привле-

кается формула Леонтьева [5]

Y D

Г в

I p v

AT'

k 7

которая находится в удовлетворительном согласии с уравнением Грюнайзена [1-5]. Здесь vk – средне- квадратичная скорость, не зависящая от направлений распространения акустических волн,

v

2 k

v L + 2 v 2 3

ρ – плотность, B A – адиабатический модуль объемного сжатия. Соотношение Грюнайзена (1) выводится из уравнения состояния, а формула Леонтьева (3) получена непосредственно из определения параметра Грюнайзе-на путем усреднения частоты колебаний решетки ω.

Формула Леонтьева привлекательна тем, что в отличие от уравнения Грюнайзена она дает возможность рассчитывать γ_D по доступным экспериментальным данным. При ее выводе использована теория упругости, которая справедлива для идеальной изотропной сплошной среды. Поэтому эта формула применима прежде всего к квазиизотропным телам типа стекол.

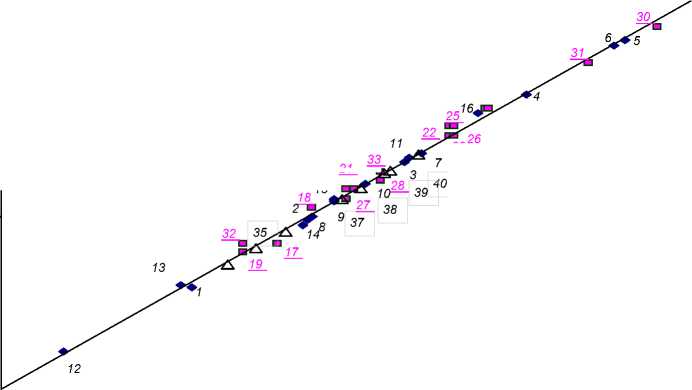
С помощью формулы Леонтьева (3) мы рассчитали параметр Грюнайзена для кварцевого стекла SiO 2 и для пяти групп двух- и трехкомпонентых стекол: Li 2 O–SiO 2 , Na 2 O–SiO 2 , Li 2 O–Na 2 O–SiO 2 , Li 2 O–Al 2 O 3 –SiO 2 и Na 2 O–Al 2 O 3 –SiO 2 с разным содержанием окислов (табл. и рис. 1). Были использованы данные из работ [6-8]. На рис. 1 приводится зависимость параметра Грюнайзена γ D от отношения скоростей акустических волн v_L / v_S для этих стекол. Как и следовало ожидать, указанная зависимость оказывается линейной и описывается эмпирическим соотношением (2).

Ранее было показано [4], что у кристаллических твердых тел одного класса постоянные С 1 и С 2 в соотношении (2) практически совпадают, так что выражение (2) принимает вид

Y d = С I v L "  v ^S

I vs где С ≈ const C1≈ C2. В частности, у щелочногалоидных кристаллов C2 ≈ 2.

Следовательно, для них параметр Грюнайзена определяется относительной разностью скоростей распространения продольной и поперечной акустических волн. Легко убедиться, что исследованные нами стекла также подчиняются данной закономерности (4): зависимость γ D от (υ l – υ s )/υ s выражается прямой, проходящей через начало координат.

Интересно отметить, что в отличие от кристаллов [3, 4] экспериментальные точки для всех исследованных стекол ложатся на одну прямую (рис. 1). Известно, что ионы щелочных металлов (лития и натрия) в щелочносиликатных стеклах располагаются в пустотах кремнекислородной сетки (– Si – O – Si –), а ионы алюминия в алюмосиликатных стеклах, например, типа Na2O – Al2O3 – SiO2, встраиваются в саму кремнекислородную сетку. Следовательно, эти стекла, вообще говоря, отличаются по структурам.

Тем не менее данные ложатся на одну прямую (рис. 1). Можно предположить, что зависимость (2) носит универсальный характер для изотропных стеклообразных твердых тел. Представляет интерес выяснение природы взаимосвязи между величинами v L / v S и γ D , хотя бы на качественном уровне.

Обсуждение результатов

Из теории упругости известно, что у изотропных тел отношение скоростей звука v L / v S является однозначной функцией коэффициента Пуассона μ [9]

v L = / ² ( 1 - M J                                    (5)

V s    V( 1 - 2 M )

Следовательно, вместо изучения связи между отношением скоростей распространения акустических волн v L / v S и параметром Грюнайзена γ D можно рассматривать взаимосвязь между коэффициентом Пуассона μ и величиной γ D .

Таблица Плотность ρ , скорость распространения продольных ( v L ) и поперечных ( v S ) акустических волн, модуль объемного сжатия В А и параметр Грюнайзена γ D для стекол Na 2 O – Al 2 O 3 – SiO 2 (использованы данные [6]).

Номера стекол	Состав по синтезу, мол. %			ρ ∙10-3, кг/м3	ν L , м/с	νS , м/с	B A ∙10-8, Па	µ	γ D
	Na 2 O	Al 2 O 3	SiO 2
1	15	0	85	2339	5430	3340	342	0.196	1.28
2	15	5	80	2358	5570	3390	370	0.206	1.31
3	15	10	75	2410	5697	3510	386	0.194	1.26
4	15	15	70	2465	5737	3469	416	0.212	1.34
5	15	20	65	2428	5850	3540	425	0.211	1.34
6	15	25	60	2472	6000	3568	470	0.226	1.40
7	25	0	75	2439	5280	3140	359	0.226	1.40
8	25	5	70	2455	5480	3240	394	0.231	1.41
9	25	10	65	2461	5610	3330	411	0.228	1.40
10	25	20	55	2470	5680	3450	405	0.208	1.32
11	25	25	50	2499	5790	3490	432	0.215	1.35
12	25	30	45	2519	6026	3556	490	0.233	1.43
13	35	0	65	2497	5340	3070	398	0.253	1.52
14	30	5	65	2486	5500	3200	413	0.244	1.47
15	20	15	65	2450	5670	3490	390	0.195	1.28
16	17.5	17.5	65	2447	5746	3458	418	0.216	1.35

γ

1,50

1,30

1,10

1,55

20 21 15

a

b

c

1,60

1,65

1,70

v L /v s

Рис. 1. Корреляция между γ D и ( v L /v s ) для ряда стеклообразных систем. a – стекла Li 2 O -Na 2 O- SiO 2 , содержание SiO 2 , Na 2 O и Li 2 O, мол.%: 1 – 85/15/0, 2 – 80/20/0, 3 – 75/25/0, 4 – 70/30/0, 5 – 67/33/0, 6 – 65/35/0, 7 – 67/0/33, 8 – 75/5/20, 9 – 75/10/15, 10 – 75/15/10, 11 – 75/20/5; 12 – SiO 2 ; Li 2 O-SiO 2 , содержание Li 2 O, мол.%: 13 – 16, 14 – 26, 15 – 32, 16 – 40 [8]. b – натриевоалюмосиликатные стекла Na 2 O-Al 2 O 3 -SiO 2 , номера точек соответствуют номерам стекол в табл. [6]. c – стекла Li 2 O-Al 2 O 3 -SiO 2 , содержание Li 2 O, Al 2 O 3 и SiO 2 , мол.%: 34 – 15/4/81, 35 – 15/6/79, 36 – 15/8/77, 37 – 15/10/75, 38 – 15/12/73, 39 – 15/15/70, 40 – 15/16/69, 41 – 15/18/67, 42 – 15/22/63, 43 – 33/2/65, 44 – 31/4/65, 45 – 29/6/65, 46 – 27/8/65, 47 – 25/10/65, 48 – 23/12/65, 49 – 21/14/65, 50 – 19/16/65, 51 – 17,5/17,5/65, 52 – 17/18/65, 53 – 15/20/65, 54 – 13/22/65, 55 – 20/20/60, 56 – 19/20/61, 57 – 17/20/63, 58 – 13/20/67, 59 – 11/20/69 [7]. Точки 41-59 ложатся на прямую, они не нанесены на график вследствие загромождения точек

Коэффициент Пуассона (коэффициент поперечной деформации) определяется отношением поперечной деформации тела ε z = Δ d / d 0 к его продольному удлинению ε x = Δ l / l 0 при одноосном растяжении:

µ=

ε _z

ε _x

и прежде всего характеризует приращение объема тела Δ V / V при одноосной деформации

A V / V = £ z (1 -2ц)

Коэффициент поперечной деформации μ оказывается связанным с пластической деформацией стекол [10], а также с температурой их размягчения [11]. Поскольку коэффициент Пуассона определяется деформациями, происходящими во взаимно перпендикулярных направлениях, по-видимому, он выражает своеобразную зависимость μ (следовательно, и отношения v L / v S ) от интенсивности развития процессов неупругости в реальном деформируемом теле [12].

Для реальных твердых тел с неоднородными структурами могут наблюдаться случаи отклонения от выводов теории упругости. В этом отношении интересен подход Кузьменко [12, 13], согласно которому коэффициент Пуассона реальных твердых тел отражает способность вещества противодействовать изменению объема. Высокое значение μ указывает на то, что материал может эффективно компенсировать изменение объема, возникающее на первом этапе деформирования. Чем больше μ , тем меньшей оказывается итоговая величина изменения объема твердого тела. Верхний предел μ = 0.5 следует из условия, когда изменение объема при деформировании компенсируется полностью противодействием вещества (при μ = 0.5, Δ V = 0 (6)). Это условие выполняется для жидкостей, а для твердых тел полной компенсации изменения объема не бывает, поэтому для них μ < 0.5.

По теории Кузьменко [13] коэффициент Пуассона наряду со сказанным выше характеризует долю энергии сдвига W S в общей энергии деформирования W :

W S _ 1 - 3 ц ² - 3 ц ³

W "      1 + ц

Чем больше μ , тем меньше энергия сдвиговых деформаций, тем меньше сопротивление материала сдвигу, тем ближе он в этом отношении к жидкости. Отсюда следует, что коэффициент Пуассона должен быть связан, например, с такой характеристикой неупругости твердого тела, как предел текучести – напряжение σ y , выше которого наблюдается пластическая деформация.

Материалы с небольшими пределами текучести, т.е. с повышенной мягкостью и пластичностью (золото, серебро, медь), имеют высокие значения μ , приближающиеся к 0.5, а хрупкие твердые тела (бериллий, стекла) характеризуются низкими коэффициентами Пуассона μ . В частности, кварцевое стекло с высоким пределом текучести имеет μ = 0.17 [10].

Таким образом, в рамках теории Кузьменко можно, по крайней мере, качественно объяснить наличие определенной связи между коэффициентом Пуассона (отношением vL/vS) и пластичностью твердых тел.

Недавно Пинеда [14] в рамках простейшей модели исследовал влияние структурных изменений на коэффициент Пуассона металлических стекол. С помощью этой модели, на наш взгляд, можно попытаться обосновать взаимосвязь между коэффициентом Пуассона и параметром Грюнайзена. Пинеда принимает, что потенциал межатомного взаимодействия состоит из гармонической и ангармонической частей

U(r) = a (r – r 0 )² – b (r – r 0 )³

где а – гармонический, а b – ангармонический коэффициенты, r0 – межатомное расстояние, соответствующее минимуму потенциала.

Модель основана на предположении о Гауссовом распределении расстояний между ближайшими атомами в идеальном однокомпонентном металлическом стекле. Предполагается, что упругие свойства определяются непосредственным окружением атомов – первой координационной сферой. В окончательные формулы мгновенных модулей объемного сжатия В и сдвига G входят безразмерные параметры

5 s _ —

,

r0

° i            br

° _ ---, p _ br0-, r0                a

где δ = ( r 1 – r 0 ), r 1 и σ 1 – средний радиус и ширина первой координационной сферы. Величины s и σ характеризуют отклонения межатомного расстояния от его равновесного значения r ₀ и среднюю дисперсию вблизи r ₀ соответственно. Параметр р характеризует степень ангармоничности потенциала. Он пропорционален параметру Грюнайзена γ_D = br₀ /6 a [15].

Модель Пинеды была использована для объяснения экспериментов по структурной релаксации и по всестороннему сжатию металлических стекол. В обоих процессах плотность стекла увеличивается, что приводит к возрастанию упругих модулей. Однако коэффициент Пуассона в результате струк- турной релаксации уменьшается (снижение параметра σ оказывается сильнее), но увеличивается при сжатии под давлением (здесь эффект уменьшения s является доминирующим). В целом модель качественно правильно описывает изменения упругих характеристик в этих опытах.

Мы привлекли модель Пинеды для проверки зависимости отношения упругих модулей ( B / G ) и, следовательно, коэффициента Пуассона µ , от параметра ангармоничности p . Из модели следует, что такая зависимость существует. В самом деле в соответствии с формулами упругие модули B и G пропорциональны гармоническому коэффициенту а – параметру межатомного потенциала, а их отношение B / G (следовательно, и коэффициент Пуассона μ ) практически не зависит от а и определяется главным образом параметром ангармоничности р . Отсюда следует зависимость коэффициента Пуассона μ и, следовательно, отношения v L / v S от параметра Грюнайзена γ D – меры ангармонизма колебаний решетки.

Заключение

У стекол существует определенная взаимосвязь между отношением скоростей распространения продольной и поперечной акустических волн и такой нелинейной величиной как параметр Грюнайзе-на, что может быть качественно обосновано в рамках модели Пинеды [14]. Наличие у стекол корреляции между коэффициентом Пуассона, являющимся однозначной функцией отношения скоростей звука v L / v S , и нелинейной неупругой величиной – пластической деформацией, можно качественно объяснить с помощью теории Кузьменко [12, 13].