ПАРАМЕТРИЧЕСКАЯ ИДЕНТИФИКАЦИЯ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ ЗЕРКАЛЬНЫХ МАТЕРИАЛОВ, ФУНКЦИОНИРУЮЩИХ НА ОРБИТАЛЬНОМ УЧАСТКЕ ПОЛЕТА

При проектировании теплового облика изделий или оценке их термонапряженного состояния необходимо иметь априорную информацию об их исходных данных, таких как начально-граничные условия и функции изменения теплофизических параметров от факторов эксплуатационного применения. В данной работе рассматривается метод идентификации эффективного коэффициента теплопроводности материала как функции от температуры на примере элемента зеркальной системы космического аппарата (КА), который имеет сложную физико-химическую структуру и функционирует на орбитальном участке полета. При моделировании теплового режима данного объекта необходимо знать его эффективные теплофизические свойства, поскольку процесс теплообмена сопровождается как лучисто-кондуктивным теп-лопереносом на поверхности материала, так и переносом лучистой тепловой энергии внутри него.

ПОСТАНОВКА ЗАДАЧИ ТЕПЛООБМЕНА

Первым шагом в восстановлении коэффициента теплопроводности конструкции является составление "прямой" задачи теплообмена, моделирующей условия эксперимента.

Применительно к данной постановке задачи можно использовать упрощенную одномерную схему теплопроводности при допущении о малом перераспределении теплового потока по поверх ности конструкции при ее одномерном нагреве:

С эф ( T ( x , τ ))

д T ( x ,т ) д т

^д я (Tivrw⁵T ⁽ x^,т ) .^д q изл ⁽ x^,т )

д x               д x          д x

Т = Т ■

1     10;

^д Ч изл ^{( x ,т} )    „(гт,..^ 3 ^дт,¹ _V)^e T ⁽ l x ^,т )

----д x----= £ ( T ⁽ x,т ) ) X эф ⁽ T ^{( x},^т ) )--- д x

- Ч изл ^{( x,т})5 ( x , T ) n ⁽ x ^).

Здесь:

T — температура, К;

x — линейная координата, м;

τ — время, с;

l x — длина образца;

C эф ( T ) — эффективная объемная теплоемкость материала, ^Дж ;

Х эф ( T ) — эффективная теплопроводность материала, ^т ;

м ■ К qизл (x,τ) — удельный тепловой поток, погло-

Вт щаемый оптическим зеркальным слоем, 2 ;

м2

s(T) — отражательно-излучательная характе- ристика материала;

n ( x ) — коэффициент преломления среды.

Выражение для толщины оптического слоя δ имеет вид:

lx g _ 1 J e=(T(x,t )xdx lx 0

Граничные условия имеют следующий вид:

d x       ’

^ ^{d T (} l x^{, T} ) = A ( T ( кT ) ) q_s + эф d            s x s

+s( T (lx,T ) )[ qпереизл + qamM - ^T( lx,T )4 ] , где:

µ_s — относительный мидель поверхности, на которую падает солнечный поток, по направлению на Солнце;

α — среднее альбедо планеты;

S ₀ — солнечная постоянная в окрестности планеты;

C 1 , C 2 — константы, определяющие собственное излучение планеты, при этом для планет с плотной атмосферой (в частности, для Земли)

C 1 _ ⁽ 1 ^- a ) S ⁰ ; C 2 _ 0;

φ 1 — угловой коэффициент между поверхностью и планетой, определяющий долю собственного излучения планеты, попадающую на поверхность;

φ 2 — комбинированный угловой коэффициент, зависящий от взаимного положения поверхности, Солнца и планеты, определяет долю отражeнной от планеты солнечной энергии, попадающую на рассматриваемую поверхность.

где

A_s ( T ) — поглощательная способность материала в солнечном спектре;

q_s — солнечный удельный тепловой поток, Вт

2; м qатм — атмосферный удельный тепловой по-

Вт ток, 2 ; м

Вт

σ — постоянная Стефана – Больцмана, ; м²К⁴ q_{переизл} — падающий переизлученный тепловой

Вт поток между элементами конструкции, .

м2

ОПРЕДЕЛЕНИЕ ПАДАЮЩЕГО УДЕЛЬНОГО ИНТЕГРАЛЬНОГО ТЕПЛОВОГО ПОТОКА

Плотности падающих тепловых потоков опре деляются по следующим формулам [1]: прямой солнечный поток qc = MSS0;

отраженный от планеты солнечный поток q0Z= aS 0^2;

собственное излучение планеты qco6 _ С1Ф1 + С2Ф2,

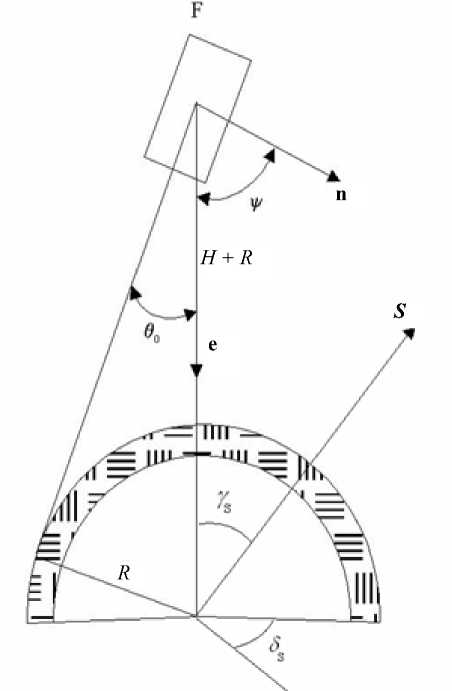
Рис. 1. К расчету угловых коэффициентов ϕ 1 и ϕ 2

Векторы и углы, фигурирующие в формулах, приведены на рис. 1.

Относительный мидель поверхности определяется следующим выражением [1]:

_ (n, S) + |(n,S)| где n — единичный вектор нормали к поверхности; S — единичный вектор, направленный на Солнце.

Направляющие косинусы векторов n и S определяются в связанной с аппаратом правой системе координат.

Углы ψ , γ s и δ s представляют собой:

ψ — угол между нормалью к площадке F, для которой рассчитываются падающие лучистые потоки, и направлением на центр планеты;

γ s — угол между направлением на площадку F из центра Земли и вектором S направления на Солнце;

δ s — угол между вертикальной плоскостью, содержащей нормаль к поверхности, и вертикальной плоскостью, содержащей вектор направления на Солнце.

Величина θ 0 (угол полуобзора планеты) определяется следующим образом:

9 = arcsin ------ , где H — высота полета.

Формула для определения углового коэффициента φ 1 имеет вид:

2π cos V Sin 9O    при 0 - V -^ — 9O;

cos ψ sin² θ ₀ π

П

- + ar^csin^(ctg v ctg ⁹ +

Ф 1 =1

+ — π

9 _O — cos² v sin ψ

;

—

—cos 9 _O ^ sin² 9 _O — cos² v π

ππ

пРи- — 9o - V -- + 9o.

Угловой коэффициент φ 2 вычисляется следующим образом:

Ф2 = f* 9o, V) cos(Ys) + f' sin V sin( Y) cos 3S, где функции f*(9O,v) и f3* (9O,v) определяют точное решение в интервале O - v - п /2 — 9O (поверхность F в этом случае не пересекает планету) и аппроксимируют точное решение с погрешностью менее 1% при п /2 — 9O - V - п /2 + 9O, при этом функции выражаются следующим образом [1]:

^f * ^{( 9} o , V ) = f '( ^ A Ф М, V ) = k ⁽⁹ o ) Ф 1 ⁽⁹ o, V );

sin²( θ ₀)

f9 = 4

(

1 + sin2 90 + 2 sin3 90 + cos4 9n, 1 — sin ^ ) ---------- In------------- I;

2sin 9 _O   1 + sin 9 _O J

f3* (9oV ) = f3 (9o)             при o < v - пi2-6o,

J            п f3 (9o) —d— при п/2-9o-v - п /2 + 9o;

I            29o cos2 9o(3 + sin2 9o),„ 1 — sin 9o f3(9o)         1 r a ln 1 a

16sin 9 _O        1 + sin 9 _O

(1 — sin 9 _O )(3 + 3sin sin 9 _O + 2sin² 9 _O)

.

Расчет углов проводится на основе траекторных параметров (перицентра, апоцентра орбиты, наклонения, аргумента перицентра, даты старта) и ориентации КА.

Угол γ s находится из скалярного произведения векторов S и n 0

cos Y s = Sn o ;

n 0 — единичный вектор нормали к плоскости орбиты КА, дополняет радиус-вектор КА и вектор скорости КА до правой системы координат.

Для γ_s после тригонометрических преобразований получаем следующее выражение:

sin /s = cos( i )sin(3) — sin( i )sin(y)cos(3), где i — наклонение орбиты (угол между плоскостью небесного экватора и плоскостью орбиты);

Y = v - О ( v — прямое восхождение Солнца: угловое расстояние по небесному экватору от точки весеннего равноденствия до меридиана Солнца, О — долгота восходящего узла, отсчитываемая от точки весеннего равноденствия).

Величина δ определяется из соотношения

3 = arcsin[sin(235)sin v .

Атмосферный удельный поток равен сумме теплового потока за счет рекомбинации атомов и молекулярного потока:

q amM q ^{+ q}мlол ^.

Удельный тепловой поток за счет рекомбинации атомов вычисляется по формуле [1]:

q = ^ N v -N- ,

F где N — число атомов газа в единице объема; ζ — эффективность рекомбинации атомов газа (ζ < 1); E1 — энергия рекомбинации на один атом газа; υ — скорость движения КА по орбите; FN — площадь проекции поверхности F на плоскость, перпендикулярную направлению скорости, F — площадь поверхности F.

Удельный молекулярный тепловой поток равен:

зависимость искомых теплофизических характеристик от температуры. В данной работе используются линейно-непрерывные базисные функции, имеющие следующий вид [2–4]:

N m (T ) H

[ °

T — T m — 1

пР^и T <  ^Tm — 1 ,

m e 1, M ;

T m

—

т m—1

при T m — 1 <  T <  T m ,

пРи ^T >  T m ,

1 F

(ь. = a«pH H) v —, 2        FN где α = 0.9÷1.0 — коэффициент аккомодации; ρ — плотность атмосферы на данной высоте, кг3 . м3

Выражение для переизлученного теплового потока имеет вид:

qnepeuaji quad (1 ej VT , где qпад — падающий удельный тепловой поток, Вт

2 . Угловой элементарный коэффициент излуче-м2

ния φ ij может быть найден из выражения:

cos( ω_i ) cos( ω_j )

j

λ p — параметрическое значение коэффициента теплопроводности зеркального материала, ^т .

м ■ К

Определим количество M временных блоков, в каждом из которых K_m ( m e l, M ) шагов т по времени и на каждом из которых коэффициент λ p в линейных комбинациях постоянен.

Это количество определим из верхней оценки функциональной невязки:

Km8f < 8sum , где Km — число узлов с замерами температуры по времени; δsum — суммарная погрешность, δf — ошибка замера температуры.

Отсюда получаем количество K_m временных шагов τ в каждом m -м блоке

K m

δ sum 6 δ_f ^2.

индексы i , j — номера излучающих поверхностей элементов; l ij — расстояние между центрами поверхностей, м; ω i , j — углы между нормалью к излучающей поверхности и направлением на излучающую поверхность.

Если теперь весь временнόй промежуток [0, т max ] разделить на число K m временных слоев в каждом блоке, получим количество M конечных элементов

τ

M = -max , K m

АЛГОРИТМ ИДЕНТИФИКАЦИИ ЭФФЕКТИВНОГО КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ

Представим теперь эффективную теплопроводность через коэффициенты в параметризирован-ном виде, умноженные на соответствующие базисные функции, учитывающие зависимость от температуры:

M

^эф (T) »Z ^pNm (T), m=1

где N m ( T ) — базисные функции, описывающие

а длина A T_m каждого конечного элемента m e 1, M равна:

T a t _ max m

—

M

T

-min- ,   m e l, M .

Максимальное значение температуры может быть оценено из следующей постановки задачи [5–8]:

с ,ф ( T ( - ) )- ^T m=^xi - ⁾ _ A , T„ x - ) q , +

о

+ eT  (- )[ q     + q   — oT  ( — )⁴];

max        переизл атм       min

T max (O) = T ° .

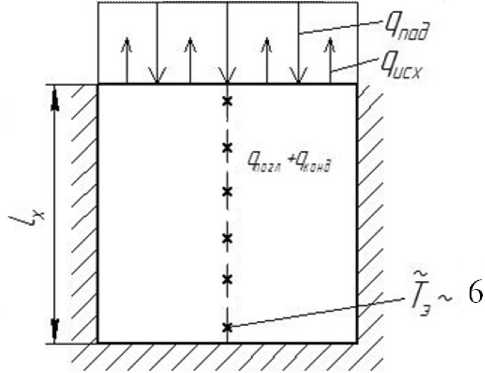
Рис. 2. Схема теплового нагружения объекта испытаний.

Звездочками схематично изображены места установки термопар

В работе используется метод безусловной минимизации функционала S ( λ _p ) c помощью градиентного метода сопряженных направлений как наиболее точного метода первого порядка, позволяющего достичь требуемой сходимости за минимальное число итераций.

Последовательный алгоритм метода сопряженных градиентов можно представить в следующем виде [12–17]:

X p+1 = X p + AX p+1, где

A X P ^{+ 1} =- в к P n .

Направление спуска определяется из соотношений:

p n = grad( X n ) + в п p n X в о = 0, p ⁰ = grad 5 ( X 0);

А минимальное значение температуры — из выражения:

С эф ( T T) ^ TT

= ^Х эф ⁽ T ) T nm ^{( т} ) [ ^T max ^{( т} ) - ^T _ml n ^{( т} ) ] + Ч изл ⁽ l x , ^Т X

T min (O) = X

Решив эту систему, было определено оптимальное количество временных блоков M , равное 3. Везде далее суммирование ведется по ним.

Схематичный вид образца приведен на рис. 2.

Рассмотрим восстановление искомых теплофизических характеристик прибора на основе среднеквадратичного функционала невязки между теоретическим и экспериментальным полями температур [9–11]:

τ max                                   2

⁵ X ) = у JE [ TX ) - T ( x^ ) ] d T .

P n =

grad S ( λ ⁿ )²

| grad 5 ( X ^{n - 1})|^2.

Погрешность входных данных δ _sum, вычисленная в той же метрике, что и целевой функционал:

5 =5 + 5,+5 +5 sum a f окр x где:

δ f — погрешность входных температур, определяемая следующим выражением:

τmax M sf = J E 5l (т )dT;

0 L =1

δ окр — погрешность округления полученных значений;

δ а — случайная погрешность измерений;

δ x — погрешность постановки задачи, определяемая как

С эф ( T ( x , т ) ) ^{5 T}^^X , ^T ) -^ Х эф ( T ( x , т ) ) ^d T ( x , ^T ) о т     о x               d x

^d q „3„ ^{( x ,T} ) d x

d T ( x , т )

^Х э^{ф (} T ⁽ x ^{, T} ) )    d _x

Как видно из выбранного метода оптимизации, первостепенной задачей является отыскание градиента среднеквадратичной интегральной ошибки:

a s (X p ) a A p

^T mx^r       *    15 T ( X )

= J E [ T ( X p ) - T ( x,T) ] d T .

0                         ^{d X} p

Для нахождения производной температуры по параметризированному значению теплопроводности достаточно продифференцировать основную постановку задачи теплообмена:

Получим:

α

д _:Шх,тп д Т ( Т ( х,т ) )

τ max

Т (А р ) - Т ( хт) д Т (А р )

d τ .

д Т

д т

6( х ,т ) +

д А р

+ С» (Т (х ,т) )д^ дт д\дА(ф (Т(х,т)) аТ(х,т)

д х

д Т      д х

9( х ,т ) +

^{д У ( х ,т} ) I.^{д 2} q изл ^{( х ,т} )

-эф ( Т (х,т ))-------- +   - -,---- дх  J    дх дАр

Таким образом, данный алгоритм включает в себя следующую последовательность действий:

• 1.    Задание начальных приближений параметрических величин теплофизических характеристик.

• 2.    Решение "прямой" задачи прогрева конструкции в одномерном приближении, моделируя условия наземной тепловакуумной отработки изделия.

Производная от толщины оптического слоя:

д8( х, Т)_ 1 lC .(Т) х д^( х ,V) eх дТ     1х {

Граничные условия примут следующий вид:

^ (0, Г)1 _— 0;

Эх ’

82ффТТдаТ(1х,т) — 8As (Т(/х,т)) дТ(1х,т)

дт     ах         ат       ах

+ 6^ ег.р ([ qn   + q; ] - ат (/х ,т)4 )- д тх

• - 4 ^ ( Т ( / х ,т) ) оТ ( / х ,т)³0( / х ,т ).

Данная постановка задачи решается конечноразностным методом по явной схеме, где конечноразностная аппроксимация температур в узлах уже известна из решения "прямой" задачи прогрева.

Для нахождения шага спуска α сп , исходя из метода итерационной регуляризации [9], запишем выражение целевого функционала на следующей итерации:

5 (А р +М р ) — 5 (А р ) - а с_П

8⁵ ( ^А р ) "² д А р _

;

5 (А р +А А р ) —

• - ¹ V ^T Г            д Т (А р ) |²

• 3.    Получе н ие э к сп е римента ль но г о темп е ратурного пол я изде ли я в ме с тах установки датчиков темп е ратур.

• 4.    Со с тавлен и е среднекв а дратичной интегр а ль н ой ош и бк и между те оре тичес к им и экс п ериме н тальны м температ урн ыми полями в местах ус т анов к и датчиков темпера ту р.

• 5.    Р е шение д в ух соп ряж енн ы х зада ч по поис к у комп он ент г ра ди е нта ц ел е вого ф у нкционала нев язк и ме ж д у теоре ти чес к и м и э кс п еримен та ль н ым темп е ратурны м и полями.

• 6.    Вы чи сле н ие шага с п ус к а в ме тод е соп р яж е нн ы х на п ра в лений на ос нове ме тода и т ер а ционной рег у л яри зации.

• 7.    Получе н ие с лед у ющи х и терирова н ных приближе н и й и с к омы х п а раметри че ских в еличин.

• 8.    Пров е рка к ри терия оста н ова и тера ц ионног о процесс а . В с л у ча е его в ыполнения параметризи-рова н н ы е величины счита ю тся искомыми, иначе — н еоб ход имо по в торн о в ыполн ить пункт ы 1–7.

2 EJ ^ ^{Т (А р} )   ^а сп   д А _р  ]    ^Т ( ^{х , т )]а т .}

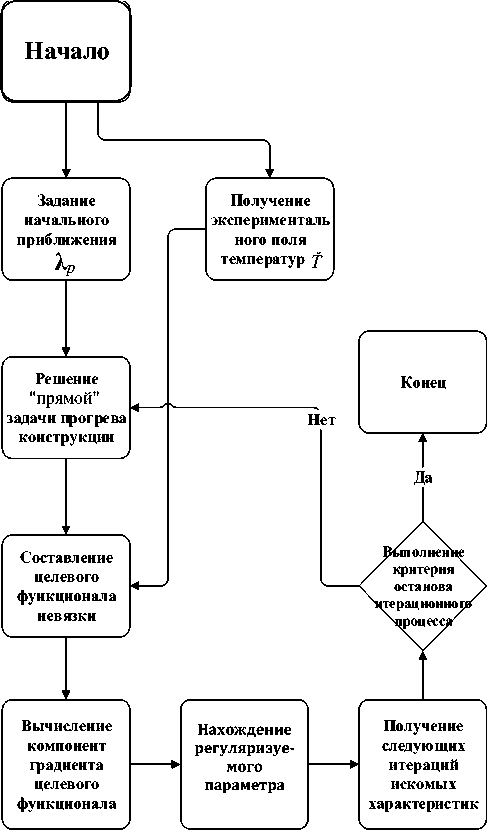
Рис. 3. Блок-схема алгоритма идентификации искомых теплофизических параметров

Откуда, согласно принципу глобального минимума, необходимо и достаточно приравнять полученное выражение нулю и выразить шаг спуска.

Р е ализац и я реше н ия данн ог о а л г оритма п роиллюстрирована блок-схемой на рис. 3.

ЧИСЛЕННЫЙ ВИРТУАЛЬНЫЙ ЭКСПЕРИМЕНТ И РЕЗУЛЬТАТЫ РАСЧЕТА

В числ е нном экс п ерим е нте рас с матрива е тся образ е ц в вид е п а раллелепипед а , п о то лщине которого установлено 6 термопар ( ри с. 2) . Все его поверхн ос ти тепл ои золи ров аны , кроме ве рхн его осн ов ания, н а которое п ад а ет лучис ты й ин т егральный тепловой поток. Таким образом , ре ализуе тс я одн о ме рн ый прог р е в п о толщине ма те риала, моделирующ и й зад а нн у ю п остановк у за д ачи. В к а чес тв е и с точн и к а теплов о го п оток а и с пользуетс я м едн ы й линей ча тый н агревате ль. Р е зуль та ты опре д еления пада ю ще г о те п лов ог о п ото к а и э к спериментального темпе р а ту рного поля пре д ставлены на рис. 4 и 5.

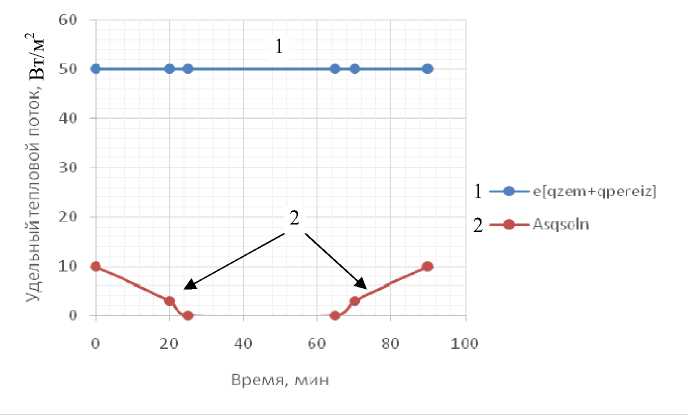
Рис. 4. Уде л ьные п ад а ющ ие теплов ые потоки на н агрев а емую поверхность образца.

1 — солнечный те п л овой поток, 2— инфракр а с н ый з е м н о й и атмосферный теплов ые п о т оки

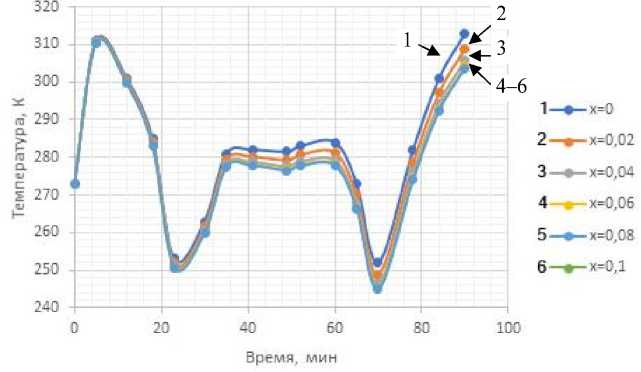
Рис. 5. Т е мп е ра т у рное п ол е в мес т ах у с тановки датчиков температур.

1–6 — н о м е ра т е рмоп а р

При итерационном уточнении параметризиро-ванной величины коэффициента теплопроводности материала будет также по итерациям восстанавливаться температурное поле, стремясь к своему экспериментальному аналогу. На рис. 6 приведены кривые температур в точках замера в разные моменты времени в зависимости от номера итерации.

Как видно из рисунка, для итерационной сходимости к своему итерационному постоянному значению необходимо 3 итерации, что говорит об эффективности предложенного метода.

Нагляднее всего процесс сходимости показан по минимизации среднеквадратичного отклонения теоретического температурного поля от экспериментального в местах замера температур. Данный процесс показан на рис. 7.

OJ

>

ф

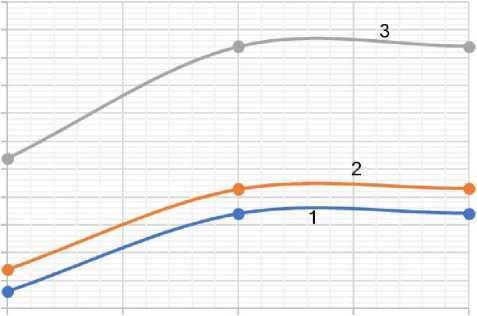
2—#—7(0,41)

Номер итерации

Рис. 6. Итерационное изменение температурного поля

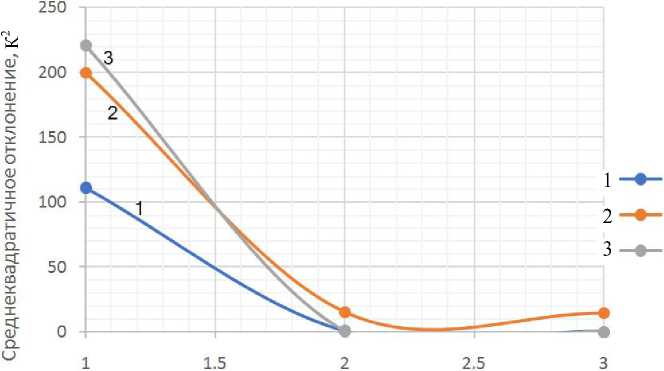
Рис. 7. Итерационное изменение среднеквадратичной ошибки между теоретическим и экспериментальным температурными полями в местах установки датчиков температур.

1-3 — временные блоки

Номер итерации

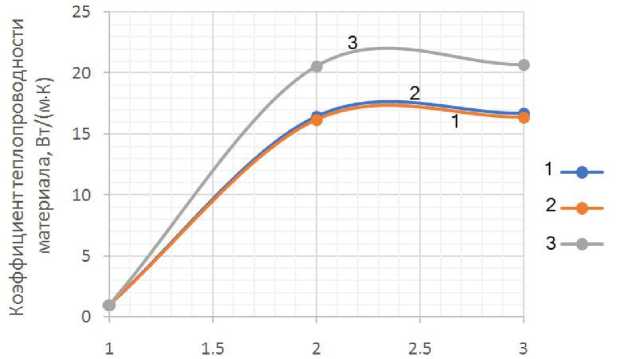
Номер итерации

Рис. 8. Итерационное изменение коэффициента теплопроводности материала от температуры.

1-3 — временные блоки

Температура, К

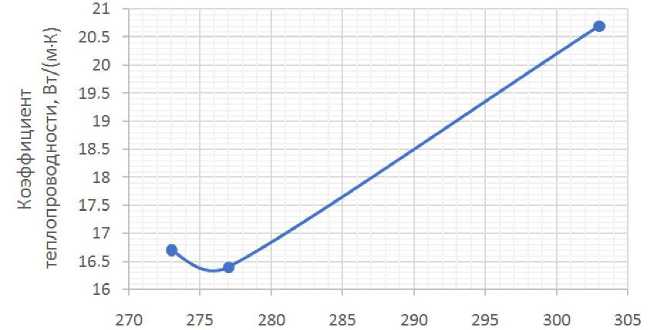
Рис. 9. Изменение коэффициента теплопроводности материала от температуры

Итерационные изменения коэффициента теплопроводности материала представлены для каждого из временных блоков на рис. 8, а изменение коэффициента теплопроводности от температуры показано на рис. 9.

ВЫВОДЫ

• 1.    Разработан метод параметрической идентификации коэффициента теплопроводности зеркальных материалов как функции от температуры методом итерационной регуляризации в приближении однонаправленного прогрева для КА на орбитальном участке полета.

• 2.    Продемонстрированы результаты данного алгоритма на примере определения коэффициента теплопроводности элемента зеркальной поверхности космической обсерватории.

• 3.    Результаты показали, что при данном уровне температур коэффициент теплопроводности будет варьироваться в пределах 16.5–21 ^т .

• 4.    Данный алгоритм может быть использован и для более широкого температурного диапазона для определения коэффициента теплопроводности материалов в изотропном приближении.

м ⋅ К