Параметрическая идентификация математической модели ЭШП

Экспериментальное определение теплофизических параметров в плавильном пространстве электрошлаковой печи в условиях высоких температур, химически агрессивной среды и оптически непрозрачных сред - задача достаточно сложная. В таких условиях наиболее эффективным решением является математическое моделирование.

При выводе уравнений приняты допущения: теплофизические параметры воды, стенки кристаллизатора, электрода, слитка не зависят от температуры, отсутствует диссипация энергии. Теплообмен плавильного пространства с внешней средой отсутствует. Ввиду цилиндрической формы печи ЭШП рассматривается осесимметричная задача.

Математическая модель теплофизических процессов при электрошлаковом переплаве [1] представлена уравнениями для областей

D_x = {х, т : 0 < х < z, 0 < т <  т_к };

Z)2 = {х, т : z < х < с, т > 0};

D₃ = {х, т : с < х <  d, т > 0};

Р₄ = {х, т : d < х < 1, т > 0}:

56в д0в           Q А д26в

5г +Ub 9х %вс(9с          йг2 ’

-ту = Хсв (6_В - ⁶С)+Хс, / (6, - 0_С) + а_с —у;

от                                 Эх

7(1)

ао, ао, /Q Q а а2е,''

у-+и,т-=х;с(бс-е,)+чугт+

Эт ЭхЭх

(1 ае, а2е,)"

+а,--- +—^ ,

Г 6г 6г2 , где Ху=^у,г=\,2, 3,4.

PiCiSj

Систему уравнений (1) дополним начальными условиями:

6'(х,г,0) = ф'(х,г),ф' =[ф_вф_сф,]^Г, 1 = 1,2,3,4;

Z(O,r) = Zo,Zo=[O,O,Z(r)f на подвижной границе фазового перехода слиток твердый - жидкий металл

Реп 9^1 — ^ст [®ст (^ —       ~

-Мб=ж^ + 0,<;               (3)

Пятыгин Д.А., Порсев М.А., Суров А.Н., Чуманов И.В.

на подвижной границе шлак - оплавляющийся электрод

рш дАт = Хш [0ш (с + А - О, т)]л --Хэ [0э(с + А + О,т)^

условиями на границах областей D,: 0"0_СТ (х, г, 0) = 0_СЖ (х, г, 0) = ^;

0'(О, Г, т) = ^\г^

^[Wb Vc Vcrf; G£^k (Z, л-, т) = 0;

^CT [⁶ct (°,^r’ ^T)L ⁼ “ст,с [⁹CT (0, T) - 0_O ] ; 0_CT (z - 0, r, т) = о_сж (z + 0, г, т) = Г_пл; 0_сж(_С,г,т) = 7_ш; ОДх,О,т) = [О];

a|V(x,7?,t)] = а[о^/(х,7?,т)-0_с];

ХС1 о о

о

/ъсж

о

о о

Хн

; а =

^ст о

о

О

^сж,с о

О

О ;

6"(х, г, 0) = х^х, г); х"'О, г) = [х_в 94d,r,i) = T_m; 0_зл(с + А-О,г,т) =

Хс

= 0зл(с +А+ О,г,т) = 7^;

бшл

В уравнениях (1)—(5) приняты обозначения: индексы в, с, ст, сж, ш, э у соответствующих параметров относятся к воде, стенке, слитку твердой фазы, слитку жидкой фазы, шлаковой ванне, электроду; где 0_в, 0_С, 0_СТ, 0_СЖ, 0_Ш, 0₃ - соответствующие температуры сред; р,, с,, X, , ^ - соот

ветственно плотность, теплоемкость, теплопроводность, температуропроводность z-й среды; а_у , P_f, Sj - соответственно коэффициент теплопередачи между z-й и у-й средой, периметр раздела и площадь поперечного сечения z-й среды; И, - скорость движения z-й среды; х, г, т, z, А, с - соответственно текущие координаты по длине, радиусу кристаллизатора, время, координата подвижной границы в слитке, координата подвижной границы в электроде и граница между электродом и жидкой ванной; Т^, Т_ш - соответственно температуры плавления и шлаковой ванны; q - теплота кристаллизации; ф₇, \|/_z, ^ - известные распределения температур по соответствующим координатам; m - номер коаксиального слоя для слитка; су - коэффициент лучеиспускания; Аг - величина шага по переменной г.

Численная реализация модели, представленная системой дифференциальных уравнений (1)—(5), даёт возможность получить внутренние переменные модели в виде численных значений температур 0В , 0С, 0СТ, 0СЖ, 0Ш . Для получения, например, 0Ш использовались значения Хш=100 ккал/м-ч°С коэффициента теплопроводности шлака и аш = Хш/сшрш ,

где сш и рш соответственно теплоемкость и плотность шлака.

В данной работе разработана методика параметрической идентификации математической модели теплового режима шлака.

Задача параметрической идентификации математической модели определяется как задача отыскания таких числовых значений параметров 0Ш , аш, Хш, при которых расчётные значения выхода модели наилучшим образом согласовались бы с экспериментально полученными данными. Необходимость решения такой задачи обусловлена тем, что существуют трудности по измерению Хш [2]. Поэтому такой параметр лучше всего определять по экспериментальным данным. Как видно из расчётных и экспериментальных данных на участке идентификации их близость может оказаться неприемлемой.

С целью повышения точности настройки модели на реальный процесс целесообразно решить задачу параметрической идентификации, которая сформулирована следующим образом:

7^,6^)= If (е?-9^ mm .

Y И _z=j

Исходной информацией в данном случае является модель и экспериментальные данные. Находим зависимость 0(г,Х_ш) как функцию, зависящую от радиуса г и коэффициента Х_ш :

1. При Хш= 25 ккал/м-ч °С, радиусе г = (0,05; 0,10; 0,15; 0,20; 0,25) и температуре шлака 0^ = = (1444; 1553; 1561; 1519; 1397) получим зависимость, которая изображена на рис. 1. Получим значение функции

= ^| (33489 + 5041 + 1521 + 3249 + 34596) «125 .

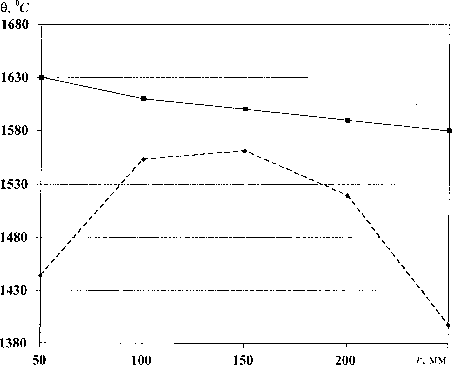
- -*- - Расчетная

—■— Экспериментальная

Рис. 1. Распределение температуры в зоне шлаковой ванны

На рис. 1 видно, что расхождение между расчетными и экспериментальными данными увеличилось.

• 2.    При Х_ш = 40 ккал/м-ч-°С, радиусе г = (0,05; 0,1; 0,15; 0,2; 0,25) и температуре шлака 9^ = = (1539; 1592; 1584; 1542; 1431) значение функции И 5           2

• 3.    При Х_ш = 50 ккал/м-ч°С, радиусе г = (0,05; 0,1; 0,15; 0,2; 0,25) и температуре шлака 9^ = (1575; 1609; 1596; 1556; 1451) значение функции F₃ « 65 .

• 4.    При Х_ш = 75 ккал/м ч °С, радиусе г = (0,05; 0,1; 0,15; 0,2; 0,25) и температуре шлака 9^ = (1624; 1635; 1617; 1581; 1489) значение функции F₄ « 43.

• 5.    При Х_ш =100 ккал/мч-°С, радиусе г = (0,05; 0,1; 0,15; 0,2; 0,25) и температуре шлака 0щ = (1647; 1648; 1629; 1597; 1515) значение функции F_s « 3 6.

• 6.    При Х_ш =110 ккал/мч-°С, радиусе г = (0,05; 0,1; 0,15; 0,2; 0,25) и температуре шлака 9$ = (1653; 1652; 1632; 1601; 1523) значение функции F₆ « 3 6.

• 7.    При Х_ш =115 ккал/м ч °С, радиусе г = (0,05; 0,1; 0,15; 0,2; 0,25) и температуре шлака 9? = (1656; 1653; 1634; 1603; 1526) значение функции F₁ « 36.

• 8.    При Х_ш = 125 ккал/м-ч-°С, радиусе г = (0,05; 0,1; 0,15; 0,2; 0,25) и температуре шлака 9^ = (1660; 1656; 1636; 1606; 1532) значение функции F₈ « 37.

• 9.    При Х_ш = 150 ккал/мч°С, радиусе г = (0,05; 0,1; 0,15; 0,2; 0,25) и температуре шлака 9щ = (1668; 1660; 1641; 1613; 1545) значение функции F₉ « 38.

• 10.    При Х_ш = 200 ккал/м-ч-°С, радиусе г = (0,05; 0,1; 0,15; 0,2; 0,25) и температуре шлака 9щ = (1678; 1666; 1646; 1620; 1562) значение функции F₁₀ « 39.

^т^ОМ/ ”8L

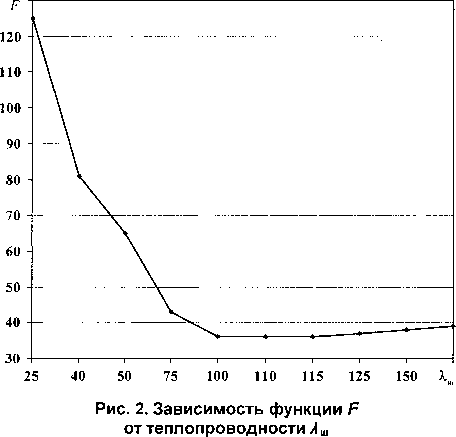
График зависимости F(XIII,9III) от Хш показан на рис. 2.

По графику (рис. 2) видно, что функция F(XUI,0UI) имеет достаточно выраженный минимум, то есть функция является унимодальной. Есть основания утверждать, что выбранный метод решения параметрической идентификации работоспособен.

На рис. 3 изображены точками экспериментальные данные, а сплошной линией построена кривая по данным значениям параметров математической модели.

Среднеквадратическая погрешность настройки модели равна 36 °C, что составляет 2 % расхождения с экспериментальными данными.

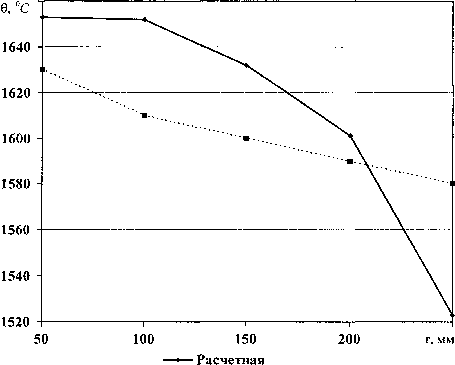
■ Экспериментальная

Рис. 3. Распределение температуры в зоне шлаковой ванны

Построенная модель, представленная уравнениями (1)-(5), позволяет разработать метод определения поля температур в шлаковой ванне, а также установить с помощью параметрической идентификации, коэффициент теплопроводности X шлака, в данном случае флюс АНФ-6. Для данной модели наиболее точное значение Хш = = 110 ккал/м-ч-°С.