Параметрическая идентификация моделей с заданными качественными характеристиками

В самом общем виде задачи параметрической идентификации сводятся к проблеме определения набора числовых параметров a = { а 1 ,..., a p } функциональной зависимости известной спецификации:

y = f (a, x). (1)

Этот набор должен обеспечивать в некотором смысле лучшее соответствие имеющихся экспериментальны х д анных y_t и значений функции ŷ_t , t = 1, m , рассчитанных в соответствии с моделью (1).

Традиционная схема решения задач параметрической идентификации может быть сведена к двухэтапной процедуре:

• 1)    на основании экспериментальных данных { x_t, y _t } , t = 1, m с использованием выбранного метода определить набор значений параметров а модели (1), что равнозначно установлению ее точного вида;

• 2)    анализ достоверности полученной модели.

Анализ достоверности модели подразумевает проверку соответствия зна чен ий эндогенной переменной y_t , t = 1, m представлениям исследователя, которые формализуются в виде некоторых критериев. К числу таких критериев могут относиться точность, адекватность, устойчивость и пр.¹, которые по своей сути являются качественными характеристиками полученной модели.

В том случае, если по результатам реализации второго этапа достигнутые значения рассматриваемых критериев не позволят считать модель достоверной, исследователю следует либо пересмотреть вид функциональной связи (1), либо уточнить и/или дополнить исходные данные, а затем вновь реализовать приведенную выше двух-

Том 29, № 4. 2019

этапную процедуру. Очевидно, что количество итераций, которые предстоит осуществить исследователю, оценить заранее сложно. Безусловно, многое зависит от компетентности исследователя, однако степень неопределенности исходных данных, обусловленная их неточностью и ограниченным количеством, может существенно осложнить процесс решения задачи параметрической идентификации.

В этой связи особую актуальность приобретают методы, по результатам применения которых будет предоставляться возможность определения параметров идентифицируемых зависимостей, заведомо удовлетворяющих всем качественным характеристикам.

Важной особенностью задач математической обработки наблюдений является наличие априорной неточности в экспериментальных данных, источниками которой могут быть ошибки измерений или ошибки, возникающие в ходе непосредственной обработки данных. Это означает, что истинные значения исходных данных неизвестны наверняка, но относительно них можно утверждать, что их значения принадлежат некоторым не всегда заранее известным интервалам:

xM е[xit,Xt], y, е[yt,у,], t = 1, m, i = 17Й. (2)

В этих условиях может оказаться нецелесообразным определение единственного набора значений параметров модели (1), так как в силу того, что для исходных данных характерна интервальная неопределенность, единственность параметров модели будет означать, что получено точное решение на основании априори неточных данных. Поэтому более уместным может оказаться поиск интервалов значений

Vol. 29, no. 4. 2019 параметров a , обеспечивающих приемлемые значения качественных характеристик.

Обзор литературы

Решение задач параметрической идентификации на основе использования статистических методов является наиболее распространенным подходом в прикладном анализе наблюдений², согласно которому по экспериментальным данным { x _t, y _t } , t = 1, m требуется определить регрессионную зависимость случайного результирующего фактора от неслучайных переменных, объясняющих его:

^{y (} x ) = f ( x ) + ^ ( x ) ,       (3)

где y ̂ ( x_̅ ) – функция, определяющая расчетные значения результирующего фактора, ^ ( x ) - ошибки измерений результирующей переменной, которые могут зависеть и от неконтролируемых факторов.

Достаточно часто основой статистического инструментария является метод наименьших квадратов (МНК), применение которого позволяет получать несмещенные, состоятельные и эффективные оценки для параметров регрессионных зависимостей (3). Согласно МНК искомые параметры должны обеспечивать минимум суммы квадратов отклонений экспериментальных и расчетных значений результирующего фактора (эндогенной переменной). При этом должны выполняться определенные предпосылки3, являющиеся следствием условий Гаусса - Марко-ва4, которые справедливы далеко не для всех практических задач. Провер- ка справедливости этих предпосылок предполагает исследование множества всех ошибок {St = £(xt), t = 1, m}, в отношении которых должно быть установлено, что они случайны, распределены по нормальному закону с нулевым математическим ожиданием и конечной дисперсией и не являются автокоррелированными.

В некоторых случаях проблемы неприменимости классического МНК удается решить с помощью его мо-дификаций⁵. Так, например, в случае гетероскедастичности или автокорреляции ошибок измерений, причинами которых могут выступать ошибки измерений объясняющих переменных x_̅ , вместо классического МНК может использоваться обобщенный, а при определении параметров систем одновременных уравнений, двухшаговый или трехшаговый МНК. При этом и классический МНК, и все его модификации основаны на вероятностной теории статистических методов [1], согласно которой количество наблюдений должно быть достаточным для проведения расчетов, а сами экспериментальные данные должны состоять из независимых и одинаково распределенных случайных величин.

Перечисленные требования и классические предпосылки использования статистических методов в практических задачах математической обработки наблюдений могут не выполняться. Часто независимость экспериментальных данных, равно как и их одинаковая распределенность, принимаются как некоторая данность или формулируются как следствие «общих предпо- ложений», что далеко не всегда может соответствовать действительности. Помимо этого, в случае уникальных экспериментов данные априори могут не быть многочисленными, что способно осложнить проверку предпосылок МНК или даже поставить под сомнение принципиальную возможность применения вероятностных моделей, которые изначально ориентированы на исследование массовых явлений. Несоблюдение или игнорирование принципов и необходимых предпосылок статистических методов при решении задач параметрической идентификации может стать причиной получения модели, которая не будет являться адекватной объекту исследования.

В тех случаях, когда невозможно использование статистических методов, может применяться другой инструментарий [2; 3], в том числе основанный на теории нечетких множеств6 [4] или теории возможностей7. В контексте подобных ситуаций значительный интерес могут представлять и методы, основанные на обработке наблюдений в соответствии с подходом, предложенным Л. В. Канторовичем [5]. Суть этого подхода состоит в том, чтобы при опреде- лении параметров модели максимально полно использовать всю имеющуюся количественную и качественную информацию об объекте исследования. Ключевым аспектом при реализации такого подхода является выявление интервалов значений параметров модели, каждый элемент которых обеспечивает соответствие заданным качественным характеристикам.

Идеи, высказанные Л. В. Канторовичем, заложили основу нового подхода к математической обработке наблюдений, который активно развивается в рамках интервального анализа благодаря теоретическим работам зару-бежных8 [6–8] и российских авторов9 [9; 10], а также используется в отдельных научных направлениях [3; 11–13]. Одно из них связано с решением обратных задач химической кинетики при исследовании механизмов сложных химических реакций [14–17].

В настоящей работе представлен метод параметрической идентификации, основанный на использовании предельно допустимых оценок параметров при определении их интервальных оценок с учетом требуемых качественных характеристик, и его апробация для задачи построения модели химической кинетики.

Материалы и методы

Для оценки степени близости расчетных и экспериментальных данных введем в рассмотрение невязки - разности между расчетными и экспериментальными значениями переменной у :

y t ^- у, , t = I, m .            (4)

Условие того, что расчетные и экспериментальные данные (2) в каждом наблюдении не должны отличаться более чем на некоторую величину ^_t , задается системой неравенств:

I y t ^- y t | <  ^ , t = 1,m . (5)

Очевидно, что искомые параметры a = {a1,..., ap} модели (1) влияют на величины невязок. При этом для одной и той же модели могут существовать несколько наборов значений параметров, которые одинаково хорошо будут описывать наблюдения, но в то же время будут существенно различаться между собой. Совокупность наборов значений всех подобных параметров, очевидно, задает некоторую область Л*, для обозначения которой будем использовать термин «область неопределенности». В данном случае термин «неопределенность» отражает тот факт, что каждая точка из области Л* может быть выбрана для задания окончательного вида модели (1), что в свою очередь равносильно отсутствию однозначного способа ее идентификации.

a

По каждому из параметров { a 1 ,...,a p } определим отрезок:

aj е[ a, aj J, j = 1, p,      (6)

состоящий из значений aj, каждое из которых сохраняет совместность системы (5) при некоторых значениях других параметров, а вне его совместность этой системы не обеспечивается никаким набором значений параметров. Бу- дем называть этот отрезок «интервалом неопределенности», а его границы – «предельно допустимыми оценками» параметров идентифицируемой зависимости (1).

Поставим задачу определения интервалов значений параметров (6), которые удовлетворяют системе ограничений (5). При таком подходе не требуется знание статистических свойств распределения погрешностей измерений, так как в системе неравенств (5) величины {< ® } , по сути, являются характеристиками абсолютных ошибок аппроксимации, и информация об их значениях может быть доступна исследователю (например, на основании технических характеристик используемого оборудования).

Введем величину ^ = max { ^_t } . Тогда в силу условий (5) будут справедливы соотношения:

Iу t- у, । < с, t=vm, из которых следует, что модель (1) должна описывать экспериментальные данные в пределах, обусловленных величиной ξ*. Для обозначения ξ* будем использовать термин «предельно допустимая погрешность аппроксимации».

Введем в рассмотрение множество Л, задаваемое прямым произведением интервалов (6):

Л = [а 1, й1]х_х[ар, ар ]. (7)

Очевидно, что Л является аппроксимирующим множеством для области неопределенности Л * . Назовем Л «множеством неопределенности».

Будем предполагать, что требуемые качественные характеристики имеют количественное задание, то есть формализованы в виде количественных соотношений (равенств, неравенств и пр.) или критериев. Причем данные характеристики могут относиться к временным интервалам как ретроспективного, так и перспективного анализа. Очевидно, что такая информация приводит к сужению множества Ʌ и, как следствие, необходимости рассмотрения вместо него множества Л = ЛП ^, где О - множество значений параметров модели (1), которые обеспечивают приемлемые уровни интересующих исследователя качественных характеристик. Все дальнейшие рассуждения приводятся для множества Ʌ, но могут быть повторены в терминах множества Л.

Ранее было отмечено, что в число качественных характеристик целесообразно включать те, которые позволяют получить оценки точности, адекватности и устойчивости получаемого решения¹⁰. Основываясь на описанном выше подходе, в качестве характеристики точности модели примем величину предельно допустимой погрешности аппроксимации f , являющуюся мерой максимального расхождения экспериментальных и расчетных значений искомой функции. Соответствие ее значения представлениям исследователя о точности модели эквивалентно тому, что уровень данной качественной характеристики оценивается как приемлемый. Расчет предельно допустимой погрешности f в соответствии с подходом Л. В. Канторовича [18] предлагается осуществлять на основе решения оптимизационной задачи:

ξ→min

a

I y t - у,\ <  ^ , t = T m (8) ξ ≥0.

В этом случае расчет предельно допустимых оценок параметров может проводиться на основе оптимизационных задач:

aj ^ min (max), j = 1, p jaa yt - y, I < f, t = 1m.

Адекватность модели должна устанавливаться в каждом конкретном случае с учетом специфики объекта исследования.

Для оценки устойчивости решения предлагается анализировать два множества:

‒ множество значений параметров Л ={ a\ f < | y t - y j <  E (1 + 9 ), 9 > 0}, которые гарантируют приемлемое (на уровне 9 ) изменение решения к ослаблению требований на достигнутый уровень точности описания имеющихся данных f * ;

‒ множество значений исходных данных, которые обеспечивают идентификацию модели (1) с учетом «ужесточения» требований на достигнутом уровне точности описания имеющихся данных f : X' ={ r, , t=1m \ \y_t - y_t | <  О , 0 ≤ λ < 1}.

Определение точных границ областей Л и X' в случае задач больших размерностей может свестись к достаточно объемным вычислениям. По этой причине более целесообразным может оказаться выявление границ соответствующих аппроксимирующих множеств Л " и X" , имеющих более простую структуру¹¹.

Для идентификации множества Л " предлагается использовать следующий подход.

Выберем набор параметров a⁰ { a ° ,_, a^o _p } : a ⁰ еЛ * П Л (полагая, что f^* определено, а множество Л - не идентифицировано). Зададим параметр 9 и рассмотрим следующую оптимизационную задачу:

п > min nA8t}

I y'-yl < У (1 + e ), t = 1, m

• 1    - 5y|< n, 5j> 0, j = V"p    (10)

η≥0,

где yt = f (a°,xt), y*t=f (a', xt), t = 1,m, a' = {a‘j a‘ = Sjaj, j = 1, p}.

По результатам решения задачи (10) должны быть рассчитаны максимальные относительные отклонения 5₃ от каждого параметра a 0 , , которые обеспечивают заданный уровень соответствия расчетных и экспериментальных данных. По сути, это означает, что будет определено аппроксимирующее множество Л " для области Л', состоящее из значений параметров a' = aa,,..,,ap}, которые гарантировано обеспечивают для всех невязок у* _t - y t абсолютную точность, не превышающую $ (1+ e ) (рис. 1).

Если малым значениям параметра e будет соответствовать малое значение параметра п (а значит и малые относительные отклонения от точки a ⁰ ), то решение задачи параметрической идентификации, задаваемое областью неопределенности Л * , является устойчивым в точке а ⁰ относительно вариации уровней точности.

Вывод об устойчивости в целом множества Л * решения задачи параметрической идентификации может быть сделан на основании анализа результатов аналогичных расчетов для всех наборов значений параметров, лежащих на пересечении множеств Л^* и Л.

Таким образом, модель для идентификации множества X" может быть представлена в следующем виде:

Z ^ min z ,{y}

I y" - y j <  $ * -Х , t = 1, m

• 1    - Yi\ ^ z, Yi ^ 0, i = Vn (11) ζ ≥ 0,

где y _t = f ( a, x, ) ; _ y ‘= f ( a, x , ') ; x ' = = { x ’ x‘ = Y i x i , i = 1, n } ; a - произвольный элемент множества Л * ; Х - заданный числовой параметр (0 ≤ λ < 1), характеризующий желаемое изменение точности соответствия расчетных и экспериментальных данных.

Оптимальное значение целевой функции задачи (11) Z * характеризует максимальную погрешность в параметрах при заданном уровне точности аппроксимации $ * -Х . Если малым вариациям точности аппроксимации

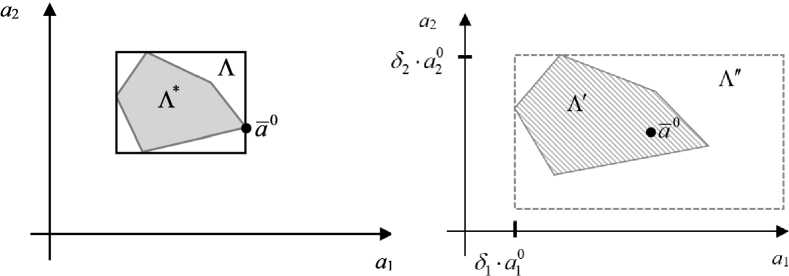
a)                                                      b)

Р и с. 1. Геометрическая интерпретация начальных условий (а) и решения (b) задачи (10)

F i g. 1. Geometric interpretation of the initial conditions (a) and solution (b) of the problem (10)

Сomputer science, computer engineering and management                                     487

(что отвечает значениям λ , близким к 1) будут соответствовать малые вариации исходных данных (то есть допустимые Z * ), то исходные данные задачи параметрической идентификации при фиксиро в анном наборе значений параметров а еЛ * являются устойчивыми относительно вариации уровней точности. Другими словами, если значение Z * соответствует представлениям исследователя о предельно допустимой погрешности измерения исходных данных, то качество исходных данных можно считать приемлемым.

Учитывая, что в формализации модели (11) присутств у ет произвольный вектор параметров а еЛ * , то для формулировки вывода о качестве исходных данных требуется рассмотреть задачи (11) V а еЛ * . Однако, если размер множества Л * небольшой (что равнозначно приемлемой неопределенности решения), и функция (1) является непрерывной, качество исходных данных может быть установлено на основе рассмотрения ограниченного множества векторов а еЛ * . В этой связи целесообразным является проведение оценки степени неопределенности решения задачи параметрической идентификации [14], что с учетом справедливости соотношения Л * сЛ может быть осуществлено с использованием предельно допустимых оценок параметров:

diam Л * = diam Л = max (a, - a Д (12) j = 1, p ^j ’’

Результаты исследования

Апробация представленного подхода проводилась на классическом примере построения простейшей модели химической кинетики для реакции «превращения дибромянтарной кислоты в бромистоводородную и бромома-леиновую»12 [19]:

С 4 Н 4 О 4 ВГ 2 = ВгН + С 4 Н 3 О 4 ВГ . (13)

Для химической реакции (13) вид кинетической модели, описывающей изменение концентрации вещества ( а ) с течением времени ( t ), следующий:

da = - ka ,        (14)

dt где k – константа скорости реакции, причем из реакции (14) следует, что k ≥ 0.

Значения константы скорости реакции k рассчитывались по формуле:

k = 1. lg—T⁰--- ,       (15)

t ⁶3T₀ -2Tn,        ^{v ;}

где T _n – титры, измеряемые в моменты времени t_n .

Для расчета концентрации дибромянтарной кислоты использовалась формула:

a n = a o |3-

V ^T0 7

,

где a ₀ – начальная концентрация.

Условиями проведения реакции гарантировалось постоянство константы скорости k . Поэтому справедливость кинетического уравнения (14) была установленной в силу того, что по результатам расчетов на основании формулы (16) получались близкие значения k .

Ниже приводятся этапы параметрической идентификации модели (14), реализованные в соответствии с представленным выше подходом. Расчет предельно допустимой погрешности аппроксимации по имеющимся экспериментальным данным (табл. 1) проводился на основе модели:

ξ →min

I а , - a ,\ <^ , i = 1,19          (17)

к > 0, ^ > 0, где ai - концентрации дибромянтарной кислоты, рассчитанные по формуле (16) на основе экспериментальных данных о титрах; ai - расчетные значения концентрации согласно модели (17) (табл. 1).

По методу Рунге - Кутты для задачи (17) было получено единственное оптимальное решение к * = 0,03122. Таким образом, был установлен точный вид модели (14):

— = -0,03122а, (18) dt и получена первая качественная характеристика - точность описания экспериментальных данных f = 0,01840 (это значение показывает, что в каждом опыте константа скорости k* (табл. 1) обеспечивает описание экспериментальных концентраций с погрешностью, не превышающей 0,01840). Константе к* соответствует обобщенный показатель точности описания данных - средняя ошибка аппроксимации14, равная 2,42 %. Интервал неопределенности по константе скорости в виду единственности оптимального значения к* является вырожденным.

Т а б л и ц а 1

T a b l e 1

Результаты численной реализации модели (17)

Results of numerical implementation of the model (17)

g. - a i a_i

t , мин. / min	T13, мг/см3 / mg/cm3	к , мин.-1 / min-1	Концентрация, мг/см3 / Concentration, mg/cm3		Ошибка / Error
			а	a i	абсолютная, мг/см3 / absolute error, mg/cm3	относительная, % / relative error, %
0	10210,0	–	1000,0	–	–	–
2	10530,0	32,4	937,3	939,5	–2,20	–0,23
4	10790,0	30,2	886,4	882,6	3,80	0,42
6	11050,0	30,0	835,5	829,2	6,30	0,75
8	11250,0	28,5	796,3	779,0	17,30	2,17
10	11550,0	31,7	737,5	731,9	5,60	0,77
13	11940,0	31,8	661,1	666,4	–5,30	–0,81
16	12290,0	32,7	592,6	606,9	–14,30	–2,42
19	12530,0	31,9	545,5	552,6	–7,10	–1,30
22	12840,0	32,9	484,8	503,2	–18,40	–3,79
26	13030,0	32,0	447,6	444,1	3,50	0,77
30	13300,0	31,0	394,7	392,0	2,70	0,68
34	13570,0	31,6	341,8	346,0	–4,20	–1,22
39	13710,0	30,8	314,4	296,0	18,40	5,85
45	14050,0	31,0	247,8	245,4	2,40	0,95
52	14320,0	31,4	194,9	197,3	–2,40	–1,21
60	14520,0	31,0	155,7	153,7	2,00	1,32
71	14690,0	29,6	122,4	109,0	13,40	10,95
90	15030,0	32,1	55,8	60,3	–4,50	–8,02

¹³ В таблице 1 T, k – экспериментальные данные / In Table 1 T, k – experimental data.

¹⁴ A = 1У

.

19 &

Кинетическая модель (18) является адекватной в силу логичной динамики расчетных значений концентраций дибромянтарной кислоты.

Анализ устойчивости модели (18) проводился с учетом того, что в идентифицируемой зависимости определению подлежит единственный параметр. Поэтому множество Л ' представляет собой интервал, границы которого могут быть найдены на основе следующих оптимизационных задач:

к ^ min (max)

|a, -a|< ^* (1+9), i = 1,19 (19) к > 0, где 9 > 0 — заданный числовой параметр, отражающий «ослабление» усло вий на степень близости экспериментальных и расчетных значений.

Оптимальное решение задачи (19) при θ = 0,15 следующее:

kmin = 0,03097 = (1 - 0,0080) к *,к max = 0,03146 = (1 + 0,0077) к *.

Модель для анализа устойчивости исходных данных относительно вариации уровней точности имеет следующий вид:

Z ^ min к ,{/„}

| a, - a i i <  С • X , i = 1,19

1 - y\ < Z, Yt ^ 0, i = 1,19 (20)к > 0, Z > 0,

Т а б л и ц а 2

T a b l e 2

Результаты численной реализации модели (20) при λ = 0,85

Results of the numerical implementation of the model (20) with λ = 0,85

t, мин. / min γi Концентрации, мг/см3 / Concentration, mg/cm3 Ошибка / Error ãi ai абсолютная, мг/см3 / absolute error, mg/cm3 относительная, % / relative error, % 0 0,001046 1000,0 – – – 2 –0,001046 933,0 939,0 –6,00 –0,64 4 –0,001046 882,0 881,7 0,20 0,02 6 0,001046 835,5 828,0 7,50 0,90 8 –0,000393 793,1 777,5 15,60 1,97 10 –0,001046 732,8 730,0 2,70 0,37 13 –0,001046 656,2 664,3 –8,10 –1,23 16 –0,000509 588,8 604,4 –15,60 –2,66 19 –0,001046 540,4 550,0 –9,60 –1,78 22 0,001046 484,8 500,5 –15,60 –3,23 26 –0,001046 442,3 441,3 1,00 0,22 30 –0,001046 389,3 389,1 0,20 0,04 34 –0,001046 336,3 343,1 –6,80 –2,03 39 –0,001046 308,8 293,1 15,60 5,07 45 –0,001046 242,0 242,7 –0,70 –0,28 52 –0,001046 189,0 194,7 –5,70 –3,01 60 –0,001046 149,8 151,4 –1,60 –1,08 71 –0,001046 116,4 107,1 9,30 7,99 90 –0,001046 49,7 59,0 –9,30 –18,75 где ai и ai- концентрации дибромянтарной кислоты, рассчитанные по формуле (16) и согласно модели (20) на основе скорректированных на коэффициент (1‒γi) значений титров.

Ниже (табл. 2) представлены результаты расчетов, полученные при X = 0,85 в соответствии с оптимальными значениями Z * = 0,00105 и к * =

= 0,03147 (средняя ошибка аппроксимации составила 2,85 %).

Таким образом, абсолютная погрешность на уровне к * может быть обеспечена за счет вариации титров не более чем на 0,105 % от их экспериментальных значений, что позволяет считать экспериментальные данные устойчивыми к вариации значений критерия точности (табл. 3).

Т а б л и ц а 3

Результаты анализа качественных характеристик модели (18)

Этап	Показатели	Выводы
Исследование на устойчивость решения к * (при θ = 0,15)	Характеристики точности: – предельно допустимая погрешность аппроксимации I * = 0,01840, долей ед.; – средняя ошибка аппроксимации Ā = 2,42 %	Решение к * устойчиво к вариации точности
	Характеристики неопределенности: – интервал по константе скорости к е [ 0,03097,0,03146 ] ; – вариация относительных ошибок [–8,02, 10,95], %
Исследование на устойчивость исходных данных (при λ = 0,85)	Характеристики точности: -    абсолютная ошибка аппроксимации ^ * ■ X = 0,0156, долей ед.; -    средняя ошибка аппроксимации Ā = 2,85 %	Исходные данные устойчивы к вариации точности
	Характеристики неопределенности: -    максимальное отклонение от фактически измеренных титров Z * = 0,00105, долей ед.; -    вариация относительных ошибок [–18,75, 7,99], %

T a b l e 3

Results of the analysis of the model (18) quality characteristics

Stage	Indicators	Findings
Solution sustainability study к * (at 9 = 0.15)	Accuracy characteristics: - maximum permissible approximation error I * = 0.01840, share units; – average approximation error Ā = 2.42%	The solution к * is resistant to accuracy variations
	Uncertainty characteristics: - rate constant interval к e [ 0.03097,0.03146 ] ; – relative error variation [–8.02, 10.95], %
Initial data sustainability study (at λ = 0.85)	Accuracy characteristics: -    absolute approximation error ξ * ⋅ λ = 0.0156, share units; -    average approximation error Ā = 2.85%	Initial data resistant to variation in accuracy
	Uncertainty characteristics: -    maximum deviation from actually measured titres Z * = 0.00105, share units; -    relative error variation [–18.75, 7.99], %

[ETS]

Обсуждение и заключение

Проведенные расчеты с позиций реализации представленного в статье подхода к параметрической идентификации функциональных зависимостей позволили получить константу скорости рассматриваемой химической реакции к * = 0,03122, которая обеспечивает приемлемые значения введенных качественных характеристик кинетической модели.

Важной отличительной особенностью метода являются возможности, которые предоставляются в части выявления свойств идентифицированной зависимости и планирования экспериментов.

Так, в рассмотренной выше задаче идентификации кинетической модели было установлено следующее. Если предположить, что погрешности в измерении каждого экспериментального значения концентрации вырастут не более чем на 15 %, то границы соответствующего интервала значений константы скорости будут отличаться от оптимальной величины к * не более чем на 0,8 %. Таким образом, зная или предполагая предельный порог в расхождениях между экспериментальными и расчетными значениями эндогенной переменной, исследователь может оценить соответствующие изменения диапазонов вариации искомых параметров. Если малым изменениям значений абсолютной точности будут соответствовать приемлемые, с точки зрения исследователя, изменения в параметрах, то полученное решение можно считать устойчивым к вариации точности.

Том 29, № 4. 2019

С использованием представленного метода идентификации могут быть определены и диапазоны вариации исходных данных, обеспечивающие лучшие значения точности соответствия расчетных и фактических значений моделируемой переменной. Так, в рассмотренной задаче идентификации кинетической модели абсолютная точность может быть улучшена на 15 % за счет изменения значений титров не более чем на ±0,105 % от их фактических уровней. Данная оценка вариации погрешности титров находится в допустимых границах для этого типа экспериментальных данных, что позволяет характеризовать их качество как приемлемое.

Анализ вариации абсолютной точности в разрезе каждого экспериментального значения экзогенной переменной может составить основу для проведения экспериментов, целью которых будет являться уточнение имеющихся данных, в большей степени влияющих на значение достигнутого уровня точности. Так, применительно к рассмотренной задаче анализ расчетных данных (табл. 2) показал, что при изменении исходных данных в соответствии с оптимальным решением задачи (17) в момент времени t = 90 минут существенно возрастает погрешность для значений концентрации. Поэтому для повышения точности воспроизведения экспериментальных данных модели целесообразным является проведение таких опытов, которые будут аналогичны осуществленным в данный момент времени.

Поступила 06.05.2019; принята к публикации 06.06.2019; опубликована онлайн 31.12.2019

Об авторах:

Все авторы прочитали и одобрили окончательный вариант рукописи.