Параметрическая идентификация модели объекта управления по переходной функции работающей системы автоматического регулирования

Постановка задачи

Из литературных и практических данных хорошо известно, что динамические свойства объектов управления по каналам регулирования обычно существенно изменяются при изменении режима их работы, обусловленного, например, изменением характеристик обрабатываемых материалов, темпа производства и т. п. Так, например, в нагревательных и термических печах коэффициент передачи по каналу «расход топлива - температура в зоне» может изменяться в процессе работы печей в несколько раз [1–4]. Изменчивость динамических параметров объектов приводит к тому, что показатели качества регулирования с неизменными настройками автоматических регуляторов тоже изменяются, причем, как правило, ухудшаются в процессе работы. Попытки выявления и использования причинно-следственных связей для отслеживания значений динамических параметров [4, 5] с целью улучшения показателей качества регулирования в целом не решают проблему из-за существенной нестабильности этих взаимосвязей. В этих условиях целесообразно периодически в процессе работы системы автоматического регулирования (САР) определять динамические характеристики каналов регулирования и периодически оптимизировать параметры настройки регуляторов по найденным оценкам этих характеристик. В данной ра- боте рассматривается решение этой задачи - задачи оценки параметров объекта управления в замкнутом контуре работающей САР и настройки входящего в ее состав регулятора.

Известны различные способы решения задачи настройки регуляторов в контурах работающей системы. При микропроцессорной реализации САР часто используются так называемые экспертные алгоритмы настройки, основанные на использовании реакции работающей системы на ступенчатое воздействие (переходной функции замкнутой системы) [6-8]. При этом применяется либо возмущение по заданию, либо возмущение со стороны регулирующего органа (по нагрузке -возмущающее воздействие ft ) на рис. 1). Последнее воздействие может быть организовано путем подачи по каналу интерфейсной связи контроллера команды перевода контура регулирования в режим ручного управления с последующим быстрым изменением положения регулирующего органа и немедленным возвратом в автоматический режим.

Рис. 1. Структурная схема системы автоматического регулирования

При этом заметим, что указанное на рис. 1 и часто упоминаемое в литературе возмущающее воздействие z ( t ) - это так называемое возмущение, приведенное к выходу объекта, в части исследования качества регулирования практически ничего не дает, поскольку передаточные функции САР для этого возмущения по любым каналам отличаются от передаточных функций САР для задающего воздействия только знаком «–». Поэтому в данной работе переходные процессы, обусловленные этим возмущением, не исследуются.

Экспертные алгоритмы настройки имеют ряд недостатков, об этом достаточно подробно указано в работах [9, 10]. В качестве альтернативы предлагается формализованная процедура настройки, основанная на частотном подходе [11–13]. Здесь в замкнутом контуре регулирования возбуждаются автоколебания, амплитуда и частота которых оцениваются алгоритмом автонастройки, а затем используются для настройки регулятора данного контура. Однако частотные методы разработаны в период, когда не существовало возможности прямого решения проблемы оптимизации настройки с помощью компьютерной математической модели САР и численных методов нелинейного программирования. Кроме того, частотная методика является графоаналитической, в ней используется ряд допущений и, как правило, велика трудоемкость применяемых процедур. К тому же точность настройки контуров регулирования такими методами уже нельзя признать удовлетворительной. В настоящее время предпочтительнее использовать формальные компьютерные алгоритмы параметрической настройки, разработанные на основе достаточно точных математических моделей САР и численных методов оптимизации [14]. Вопросы достижения требуемой точности настройки и уменьшения объема необходимых графических построений и сопутствующих им «ручных» вычислений при этом автоматически снимаются.

Решение задачи параметрической идентификации

Расчет параметров настройки регулятора должен начинаться с определения динамических характеристик объекта управления, поэтому в любом случае сначала рассматривается эта задача. Причем особенность этой задачи в данном случае заключается в том, что динамические свойства объекта управления необходимо определить по тому, как изменяется выходная величина САР при отработке внесенного возмущения либо по заданию, либо по нагрузке, т. е. по реакции работающей САР [15]. Подобные задачи идентификации в замкнутом контуре регулирования в процессе нормального функционирования системы рассматривались, например, в работах [15-18].

Известно, что динамические свойства большого числа объектов управления могут быть представлены с помощью математической модели следующей структуры:

d2 x . dx a о VT+ai T+x(t)=kоб U(t-T),                                                      (1)

dt2    dt

Управление в технических системах

где x(t) - управляемая координата; U(t) - управляющее воздействие; t - время; т - время запаздывания; коб - коэффициент передачи объекта; а0 и а1 - коэффициенты дифференциального уравнения.

В работе [14] задача параметрической идентификации модели (1) решается по экспериментальным кривым разгона объектов управления. В данном же случае эту задачу следует решить, используя переходную функцию работающей САР. Поэтому для отыскания динамических параметров объекта управления нужно использовать математическую модель всего контура регулирования, а не только уравнение (1). Дополним уравнение (1) математической моделью ПИ-регулятора, при этом будем считать, что она имеет вид:

U ( t ) = к Р е ( t ) +—— Je( t ) dt ,

L    T о     J где e(t) - рассогласование; кР, ТИ - соответственно коэффициент передачи и время интегрирования регулятора. Здесь рассогласование е(t) вычисляется звеном сравнения системы стандартным образом, т. е. по формуле s(t)=xЗД (t) -x(t), где xЗД (t) - заданное значение регулируемого технологического параметра. Возмущения по заданию и по нагрузке в модели контура регулирования (1)-(2) также реализуются известным образом [1-3].

Известно, что дифференциальное уравнение (1) описывает динамические свойства конкретного объекта управления с необходимой точностью только в том случае, если удовлетворительно определены коэффициенты а о , а 1 , к об и время запаздывания т . Рассмотрим решение этой задачи на основе современных достижений теории идентификации [19, 20].

Пусть известна экспериментальная переходная функция САР, информацию, содержащуюся в данной переходной функции, и структуру математической модели контура регулирования, представленную уравнениями (1) и (2), будем считать исходными данными для решения задачи идентификации динамических свойств объекта управления. В принципе вместо экспериментальной переходной функции может быть использована опытная реакция САР на любое возмущение как по заданию, так и со стороны регулирующего органа. Задачу идентификации сформулируем следующим образом: требуется найти такие значения коэффициентов а о , а 1 , к об и времени запаздывания т , при которых критерий идентификации

I ^{( а} 0 , ^а 1 , ^к об , ^{т )} = Z [ x Э ⁽ t i ) - x ⁽ t i ) J ⁽³⁾ 1

будет принимать минимальное значение. Здесь x ^Э ( t i ) - экспериментальное значение выхода объекта или, что то же самое, экспериментальное значение переходной функции САР; x ( t i ) - расчетное значение, определяемое по модели системы (1)–(2) для данного типа возмущающего воздействия; t i - используемые при настройке моменты времени; n - число экспериментальных точек.

Данную задачу идентификации решали с помощью программы, реализующей метод покоординатного спуска, получающиеся при этом задачи одномерной минимизации решали с помощью подпрограммы, использующей метод золотого сечения. При этом для вычисления текущих значений критерия (3) в процессе поиска оптимальных параметров уравнения (1) использовали разработанные в [14] компьютерные алгоритмы расчета переходных процессов в САР при возмущении по заданию или при возмущении по нагрузке. Причем для численного интегрирования уравнение (1) применяли метод Рунге - Кутты с погрешностью, пропорциональной пятой степени шага по времени. Для этого дифференциальное уравнение (1) предварительно записывали в виде системы дифференциальных уравнений первого порядка, т. е. в нормальной форме Коши. В связи с необходимостью обеспечения заданной точности расчета программа построена так, что между экспериментальными точками по времени укладывается целое число расчетных шагов.

Уравнение (2) для компьютерного использования представляли в дискретной форме, при вычислении интеграла применяли метод трапеций. С целью сокращения объема необходимых вычислений использовали рекуррентную форму дискретного представления уравнения (2), приведенную в работе [21]:

U ( k ) = U ( k - 1) + q ₀ -e ( k ) + q 1 -e ( k - 1), (4) где k - номер расчетного шага по времени, q о = k Р [1 + h /(2 Т И )], q 1 = k Р [ h 1(2 Т И ) - 1], h - величина расчетного шага по времени.

При тестировании разработанных программ получили вполне приемлемые результаты. Для примера на рис. 2 приведена экспериментальная переходная характеристика САР давления в металлургической печи при возмущении по заданию. В этой системе настройки ПИ-регулятора были равны: k Р = 1,256 % хода ИМ/Па, Т _И = 3,436 c. В результате решения задачи идентификации по данным этой кривой были получены следующие значения параметров дифференциального уравнения (1): а₀ = 1,709 c², а 1 = 1,404 c, т= 1,200с k _об = 0,906Па/%ходаИМ. Расчет по модели (1)-(2) при данных значениях параметров регулятора и объекта управления показал, что среднеквадратическое отклонение расчетной переходной характеристики контура регулирования от экспериментальной кривой ipjn составило 0,012Па, что вполне приемлемо.

На рис. 3 приведена экспериментальная переходная характеристика той же САР, только при возмущении по нагрузке. По данным этой кривой были получены следующие значения параметров дифференциального уравнения (1): а ₀ = 1,564 c², a 1 = 1,680 c, т= 1,200с, k _об = 0,906 Па/% хода ИМ. Расчет по модели (1)-(2) при данных значениях параметров показал, что среднеквадратическое отклонение расчетной переходной характеристики контура регулирования от экспериментальной кривой ^ I/n составило 0,010 Па, что вполне приемлемо. Различие найденных численных значений динамических параметров объекта также можно считать вполне удовлетворительным.

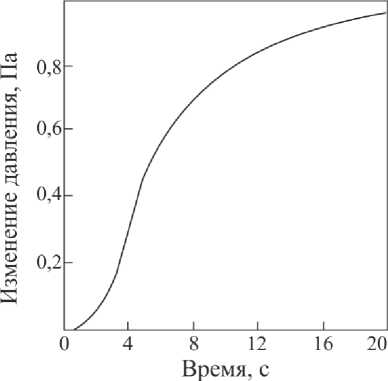
Рис. 2. Экспериментальная переходная характеристика САР давления в металлургической печи при возмущении по заданию

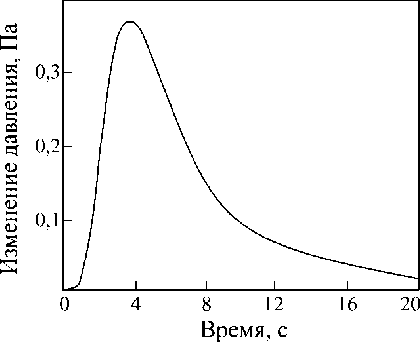
Рис. 3. Экспериментальная переходная характеристика САР давления в металлургической печи при возмущении по нагрузке

Следует заметить, что разработанная процедура настройки достаточно просто модифицируется для случая, когда вместо критерия (3) требуется минимизировать сумму модулей разностей расчетных и экспериментальных значений выходной координаты САР:

n

I ^{( a}0, ^a 1 , ^k об , ^{т )} = Е| x Э ⁽ ti ) - x ⁽ ti 4

а также для случая минимаксной задачи: это когда требуется минимизировать максимальное отклонение расчетных значений от экспериментальных данных:

I ( а ₀, а 1 , k _об, т ) ^    min max x ^Э( t_i ) - x ( t_i ) .

a 0 , ^a 1 , k об , т     i

Как известно, оценки параметров, найденные посредством минимизации критерия (3), являются наиболее правдоподобными с точки зрения нормального закона распределения ошибок,

Управление в технических системах

а для случая критерия (5) – для распределения ошибок по закону Лапласа. Кроме того, вполне понятно, что использование интегральных критериев идентификации потребует незначительных изменений в разработанных программах.

После определения динамических параметров объекта управления задачу отыскания оптимальных параметров настройки ПИ-регулятора можно решить с помощью компьютерных алгоритмов работы [14] либо по способу работ [22, 23].

Выводы

Рассмотрено решение задачи параметрической идентификации объекта управления по переходной функции работающей САР. Выполнена апробация разработанных программ по экспериментальным переходным характеристикам САР давления в металлургической печи. Указаны процедуры настройки регуляторов по найденным динамическим параметрам объекта. Результаты работы могут быть использованы при создании алгоритмического обеспечения современных многоуровневых АСУ ТП, на нижнем уровне которых применяются микроконтроллерные САР.