Параметрическая идентификация модели термодесорбции водорода

ПОСТАНОВКА ЗАДАЧИ

Водород рассматривается как один из перспективных экологически чистых энергоносителей. Кроме того, безопасность систем транспортировки и переработки углеводородного сырья во многом определяется уровнем защиты конструкционных материалов от водородной коррозии. Экспериментальный метод термодесорбционной спектрометрии (ТДС) является одним из основных при исследовании взаимодействия водорода с твердым телом [2], [3], [5]. Пластина толщины ℓ из металла или сплава, нагретая до температуры Т = T , находится в камере с газообразным водородом под давлением р . После насыщения растворенным атомарным водородом образец быстро охлаждается (отключается ток нагрева), камера вакуумируется и в условиях медленного нагрева с помощью масс-спектрометра определяется десорбционный поток. По этой информации судят о характеристиках взаимодействия водорода с материалом.

Рассмотрим симметричную по постановке эксперимента нелинейную краевую задачу ТДС-дегазации:

дс        д2с                     _

— = D(T)—, te(0,t*), хе (0,1), dt        дх2

с(0,х) = ф(х) = ф(1 - x), хе [0,1],

D(TK(t,0) = Ь(Т)сЖ te[0,tj,

D(T)cx(U) = -b(T)cl(t), t е [0, tj.

Здесь c(t, х) - концентрация атомарного водорода ( H ), растворенного в пластине, с₀ (t) = c(t, 0) , Q(t) = c(t, I) , c₀(t) = Q(t) ; t * - время дегазации; D , b - коэффициенты диффузии и десорбции; /(t) =b(T)c 2^ (t) - плотность десорбционного потока (торцами пластины пренебрегаем). Квадратичность десорбции связана с тем, что водород диффундирует в металле в атомарном

состоянии, а покидает поверхность (при х = 0 и х = I ) в молекулярной форме. Коэффициент диффузии D и коэффициент десорбции (эффективной рекомбинации) b зависят от температуры T. Как правило, в «рабочем диапазоне» с достаточной степенью приближения выполняется закон Аррениуса: D(t) = D₀exp{-E_D/[RT]}, b(T) = = b_oexp{-E b /[RT]}, D o , E d , b o , E b , R = const ( E d , E b - энергии активации, R = 8,31441 Дж/[молыК] -универсальная газовая постоянная). Нагрев обычно линейный: T(t) = T₀ + vt , v > 0 . Сокращенно D(t) = D(T(t)), b(t) = b(T(t)) .

Что касается начальных данных ф(х) , то в силу непродолжительности подготовительного этапа (охлаждение и вакуумирование) начальное распределение обычно считают практически равномерным: ф(х) = c = const . Здесь c = = СО^- , T) - равновесная концентрация. Несогласованность начальных и граничных условий при этом непринципиальна, поскольку будем использовать лишь интегральные соотношения (решение задачи (1)–(3) понимается как обобщенное). Для тонких мембран следует учесть «начальный прогиб» концентрации по краям. Ограничимся параболической аппроксимацией ф⁽х) = с - Л о^[ х - 1 о^{] 2},1 о = 1/2, Л о > 0 .

Цель работы состоит в разработке вычислительного алгоритма для определения по плотности потока термодесорбции J (t) , t е [ 0 , t * ] ( J (t) « 0, t > t * ) параметров b ₀, E _b, D_o , E _d , характеризующих водородопроницаемость материала.

Трудности решения обратных задач известны [9], [10]. В частности, разработаны градиентные алгоритмы минимизации в пространстве параметров среднеквадратичной невязки экспериментальных и модельных кривых [1]. Но на каждой итерации в общем случае приходится численно решать краевые задачи при текущих приближениях параметров. К тому же обычно сходимость локальная. Учет специфики метода

ТДС позволил разработать алгоритм идентификации, в котором основная вычислительная нагрузка связана с квадратурными формулами, а не решением краевых задач.

Для тестирования алгоритма решения обратной задачи сначала численно генерировались модельные кривые, порождающие параметры которых затем «забывались». Из-за большого разброса порядков величин при моделировании J(t) проводилось масштабирование: х = lz, z = [0,1], и = с/с , и = Du_zz , Du_z\ 0,i = ±bu 0,i , D = D/l² , b = b e/ 1 , u(0, z) = 1 - A 0 (z - 0,5)², A 0 = A 0 1 ²/c. Здесь за преобразованными параметрами модели оставляем прежние обозначения D, b, A 0 . В вычислительных экспериментах ориентировались на данные по вольфраму, являющемуся одним из конструкционных материалов в реакторах [8]: с = 5,084 х 10¹⁶ 1/см³ (К), ( Т = 1300 К), Т 0 = 300 К, Т = 2 К/c, t . = 500 с, I = 0,1 см, b₀ = 6 х 10 ¹² см⁴/с; E _b = 39,559 кДж/ моль, D 0 = 4,1 х 10^-3 см²/с; E _D =37,629 кДж/моль.

r ^l o                            r^lo

I ^(x)dx —5(t)= I C(t,x)dx ^

J 0                         ^0

Cl 0 — A 0 l g /3 — 5(t) = B(t)l 0 — A(t)l 0 /3,

B(t) = A(t)l 2 /3 + C — A 0 l 0 /3 — 5(t)/l 0 ,

^ C(t,x) = Q(t)l-1 — A(t)[x2 — lx + l2/6],

S(t) = I /(T)dT, Q(t) = 2 I J(x)dT.

J 0                    Л

Чтобы найти оставшийся функциональный параметр A( t ), подставим выражение для C(t, x) в граничное условие D(T)C_x(t,0) = b(T)c 0 (t) . Это соотношение позволяет выразить A( t ) через коэффициенты модели D, b и известную по экспериментальным данным Q( t ). Оба корня квадратного уравнения относительно A( t ) положительные, выбираем меньший из них (по физическому смыслу c₀( t ) >  0 ). Из условия V = ^с 0 ^Ь получаем соотношение для оценки D₀ , E _D, b ₀, E _b:

ПАРАБОЛИЧЕСКОЕ ПРИБЛИЖЕНИЕ

Сходимость в нелинейных обратных задачах параметрической идентификации, как правило, локальная. В рассматриваемом ТДС-экспери-менте распределение c(t, х) имеет «куполообразный» характер. Поэтому целесообразно в качественном плане за первое приближение взять параболическую аппроксимацию

c(t,x) ~ C(t,x) = B(t) — A(t)(x — l₀)²,

Ж = ³   IJ¹^)!^ — 4 ^T = t Е [0, t . ] .(6)

⁽2 )      ъи)1 )                  ULZ⁽I )

2l₀ = l, A(0) = A₀, B(0) = C.

Поскольку J( t ) соответствует модели (1) - (3), а на предварительном этапе оценки b , D используется параболическое приближение, то это равенство является приближенным.

График J( t ) имеет характер всплеска с после -дующим затуханием, причем на начальном и конечном этапах измерения менее точны. Поэтому ограничимся t Е [ t₁, t₂] с (0, t , ), , нор мируем уравнение на i_m ax = 7/ ^aX (I(t) = VJ(t)) и выделим

Считаем известной равновесную растворимость с = C(p, T) ~ VP , которая в условиях эксперимента пропорциональна корню из давления насыщения. Функция B( t ) > 0 аппроксимирует срединную концентрацию c ( t , 1 ₀), A( t ) > 0, t > 0 . Поскольку к моменту t , произошла дегазация образца (c(t,x) ~ 0, t > t , ) , определим константу A 0 в начальных данных фМ = с — A o [x — l o^{] 2} из материального баланса

безразмерные переменные:

i(t)i m1x = (Vi + 2Q(t)t ;ⁱ j m\x X — i) y, y = ^DO.    ⁽⁷⁾

I max lVbT)

t.Jmaxb(T)

^X 3D(T) '

Формально допуская E < 0, удобно считать новые переменные X(t) = x(T(t)), Y(t) = Y(T(t)) , «аррениусовскими»:

f t ,             r^l o                                      a l $

/⁽т) dr = I ^{C — A o [x — l o ]²} dx = Cl o — -°- ⁰ . (4) o               0_o                                         ³

Отсюда A₀ = 3(Cl₀ — 5 , )/l o . Величина 5 , равна половине количества десорбировавшегося водорода (в атомах), отнесенного к см² поверхности (х = 0 или х = I неважно в силу симметрии). Условия согласования Dc_x\_0l = ±bc 0, _l при t = 0 начальных данных и граничных условий дает зависимость D₀/b₀ = f₀(E_b — E_D) :

_v   ^t*/max ^b 0 _v   ⁰ = 3D ₀ ' ⁰ =

3D o

^I max l^b o

.

E x = E b —E D , E Y =E D —E b /2.

Обозначая q = 2Qt ?¹ J max , получаем уравнение

f(t;Xo,Ex,Yo,EY)=I(t)imlax

D(0)A o l = b(0)[C —A ° l 2 ]² ^ bAl  eXp^^Eb'|c A o l 2 ]² .

Перейдем к конкретизации функций A( t ), B( t ) в аппроксимации C(t,x) . Из условия баланса выразим B( t ) > 0 и подставим в C(t, x) :

.       (8)

— (V1 + q(t)X — 1J Y — 0.

Преобразуем величину У с учетом связи D 0 /b 0 = f 0 (E x ) (см. (5)):

Y = Y 0 exp{—E Y /[RT(t)]} =

= Z 0 exp{—E x /[ET 0 ]}exp {—E y /^T^]},   (9)

3[C —Aol2]2Jb;          z ч

^Z 0 =     д P 0,     ⁰ , ^z 0 = Z 0W ~ b 0 .

^A 0 ^{l I} max

Величина /_max зависит от входных данных {ф, D, b ] . Запись Z 0 = Z 0 (b₀) означает, что значения с, А₀ уже найдены, а функция J( t ) при решении обратной задачи известна. Аналогично

^“М-йУ’

tJ max ^ O ¹

3^[с - Д о ¹ о ]

^expL^E/^X b^Lv-mi' А^ о АУ (С)?

Подставляя выражения X, Y в уравнение (8), получаем зависимость / = /(t; Z₀, E_X, E_Y). Далее с учетом зашумленности реальных измерений и погрешности параболической аппроксимации следуем методу наименьших квадратов (МНК):

F(Zo,Ex,EY

^t 2

ч

f2

(т)

dr ^ min.

Производные функции F можно выписать явно (подсчет интеграла считаем элементарной операцией).

Перейдем к изложению результатов численного моделирования. Разностная схема решения задач термодесорбции изложена в [4]. График плотности потока водорода для указанных параметров представлен на рис. 1.

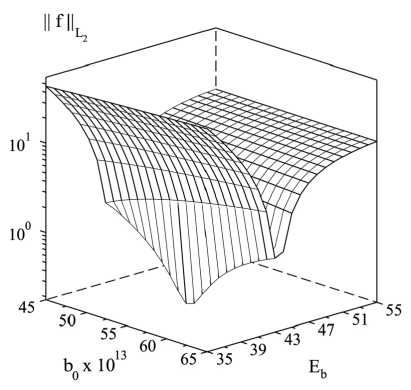
Рис. 2. Экстремум по b

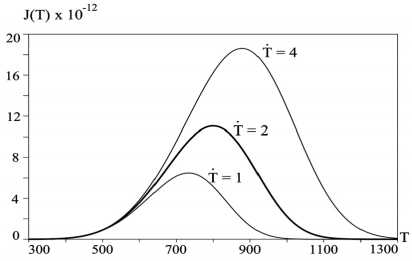
Рис. 1. ТДС-спектр. Влияние скорости нагрева

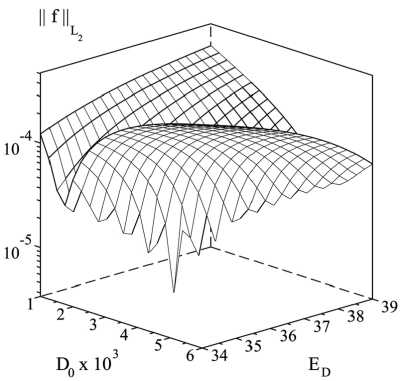
Рис. 3. Экстремум по D

Для оценки значений D₀ , E _D, b ₀, E использовались МНК и метод моментов (ММ) применительно к уравнению (8) (/ = 0), в которое подставлены: выражения X, Y согласно формулам (7); D(t) = D₀6xp{-E d /[RT] ], b(T) = b _Q exp {-E _b/[RT] ] ; T(t) = T_o + vt выражение D 0 = D 0 (b ₀, E _d , E _b) из соотношения (5). На рис. 2, 3 показано, что задача Ilf Н ь₂ ^ min (L 2 = L 2 [t 1 , t₂], t 1 = 50 c, t₂ = 450 c) хорошо обусловлена по каждому из коэффициентов D, b (один из них фиксировался равным «истинному» значению). При этом дополнительное соотношение (5) не учитывалось при построении поверхности на рис. 3, но для рис. 2 оно необходимо, иначе отсутствует экстремум в физически оправданном диапазоне.

Остановимся на уравнении /(t; Z 0 , E_X, E_Y) = 0, полученном после подстановки в (8) выражений X, Y, D 0 в соответствии с формулами (5), (7). «Истинные» значения: Z O = 0,119, E X = 1,929, E Y = = 17,849. Варьируем лишь один из параметров Z 0 , E_X, E_y Решение задачи Hf H l ₂ ^ min по Z 0 дает относительную погрешность 5(Z₀) = | Z 0 - Z O | / Z O | = 0,52. Это приводит в соответствии с формулой (9) к 5(b₀) = 0,77 и S(D₀) = 0,17 в силу (5).

Для задачи Hf Hl2 ^ min по EX имеем 5(EX) = = 1,38 (5(Eb) = 0,13, 5(Ed) = 0,07); 5(EY) = 0,26 (5(Eb) = 0,23, 5(Ed) = 0,25) для Hf Hl2 ^ min по EY.

Обратимся к методу моментов. Обозначим

^Mi = ^ i^(Zo - ^EX - ^EY⁾ =

^t 2

= I Vi(t)f(t tl

;ZO,EX,EY)dt.

Ограничимся функциями V 1 ( t ) = t/t„ V₂( t ) = t²/t,², Ф ( t ) = 10^-1 t,/t, t e [t, t ], t = 50, t = 450 (t. = 500). Использование ММ (решение системы М . = 0) дает в среднем такую же точность, как и МНК. Применение параболического приближения позволило решить обратную задачу для исходной распределенной модели с погрешностями, указанными в табл. 1. Подчеркнем, что параболическое приближение является грубым для исходной краевой задачи (1)-(3). Его задача -«попасть в порядки» оцениваемых коэффициентов D, b. Значение предэкспоненты b₀ определяется заметно хуже, что объясняется его малым

абсолютным значением (коэффициент при квадрате концентрации). Можно было бы перейти к двойной точности вычислений на всех этапах моделирования, но это излишне при зашумленных входных данных обратной задачи.

Таблица 1

Оценки параболического приближения

J n (t) = Г J о

ехp ^{ -Ц n Y ⁽ t, тУНОг) d^

Соотношение J = bc ^f ^ ^J - 4bc_o(t) = 0 имеет форму семейства уравнений для параметров: Ф ( t; D_о , E _d , Ь _о, Е _Ь) = о . При численной реализации

ряды заменялись частичными суммами:

Параметр	Исходные данные	Полученные значения	Относительная погрешность
Ьо	6 X 10-12	1,514 x 10-11	152,3 %
ЕЬ	39,559	45,100	19,8 %
D о	4,1 x 10-3	2,880 x 10-3	29,7 %
Ed	37,629	36,745	7,1 %

Ф =

^ ⁽ 0)-| j И'О dj +

Z^l         4\п^2     "I vn(t)-l^  Zn(t)j = 0

Начальные приближения E_D, Е_Ь в диапазоне нескольких десятков кДж/моль можно указать из физико-химических соображений. Приближение Ь₀(Z₀) берем в силу J(G) = Ь^Т^с^^О) = = Ь _о ехр{-Е _ЬДйТ_о] }[.С - Л_о1 о ]². Только как начальное приближение, поскольку J(G) обычно известно с большой погрешностью.

Замечание . Задача усложняется, когда равновесную концентрацию с также приходится считать неизвестной. Тогда задача четырехмерная в соответствии с (8). По оценкам Х_о, Е_х, Y_Q, E_Y значения с, А_о находятся из уравнений (4), (5).

Далее переходим к локальному уточнению оценок D_о , E_d , Ь _о, Е _Ь в соответствии с исходной моделью (1) - (3). Искомых независимых переменных 3 в силу D_о/Ь _о = f₀( Е _Ь- E _D) .

ПРИМЕНЕНИЕ ФУНКЦИИ ГРИНА

Поскольку зависимость J(t) известна по результатам эксперимента, то решение задачи ct = D(T)cxx, c(0,x) = c-Ao[x-lo]2,

С использованием пакета Scilab численно решалась задача J_t^{t 2} Ф²dт ^ min при N 1 = N 2 = 5. Уровень ошибок оценивания улучшился лишь на несколько процентов. Необходимы дополнительные соотношения.

СОПРЯЖЕННЫЕ УРАВНЕНИЯ

Следуя технике сопряженных уравнений [7], интегрированием по частям для достаточно гладкой функции ^( t, х) получим:

te Г1

0=1 I ^(t,x)[ct - Dc _xx ]dxdz =

J o ^o

= C * J(t)^(t,0)dt+ j J o                       o₀

*

J(f)^(t,f)dt +

+

j^ j o

(t)Mt)b-4t)Mt,m

-

^t *

-I D(t)^Kt)b^-4t)^ _x (t,0)dt-

J o

- cl ^(0,x)dx + A _o I (x - € _o ) ² ^(0,x)dx .

J o                     o_Q

Dc _x (t,0) = -Dc _x (t,D=J(t)

удобно представить с помощью функции Грина

[6]. Получаем следующее представление с₀( t ):

2 -.

c o ⁽t) = c-ij КПск

[ l   4^^м 1                -1

12+?2 п., ^ ; ^ехр{-" п ^к(г'⁰⁾⁾1 -

4 от t

■ l^j exp^{-^ n Y⁽t,T)'⁾J⁽r)dT,

Y⁽t,T) = j D⁽s) ds, Ц п _T

Заменим в скобке […] ^[ ехp ^{ -Ц n Y ⁽ t, 0 ^)} - 1 ^] + 1:

_ /n^\2 =       ■ экспоненту

на

Vnto =

1 - ^exp^{-Ц n Y(^{t, 0)}} [1 _—

ЦП

...]/Цп

Здесь опущен двойной интеграл, поскольку далее считаем функцию ^( t, х) подчиненной сопряженному уравнению d^/d t = - Dd^z^/d%². Кроме того, пренебрегаем интегралом от ^( t * , x)c( t * , х) по х с учетом c( t * , х) « 0 . Косвенно ограничиваемся не слишком быстро растущими по t функциями ^( t, х). Подчеркнем, что краевые условия не ставятся, «пробных» функций ^ бесконечно много. Простые варианты ^ = 1, х приводят к уравнению материального баланса, которое уже использовалось для оценки константы Л_о. Выберем, например, ^( t, х) = ^( t )expaх. При нормировке ^( t * ) = 1 получаем

^(t,x) = ехр{ a2Y(t„ t))exp{ax)^

Перепишем соотношение (11) в обозначениях ft* „ ,          f*‘             , expal + 1

X=l Jpdt, Y=l D^fb^^pdt, K = -^~—:

J _o               J_o                     exp al -1

2 ft          Vю       4v":

c o ⁽t) = ^(0) -7 I J⁽t) dj + 4A o )    v_n⁽t⁾-->    J_n(t),

1 Oo               П—4п=1        1 Z—in=l

F(a) = KaX + a²Y +

+P(0")a ² {2A o — a ² (c — A o [i o — 1ка ^ ])) — 0^

Параметр а целесообразно варьировать в пределах а 1 ~1. В табл. 2 приведены значения параметров, полученные решением системы уравнений (12) для а = 1, 8, 10, 11. Энергии активации восстанавливаются с большой точностью (их влияние на кинетику дегазации очень велико). Предэкспонента Ь 0 определяется хуже вследствие ее малого абсолютного значения. Погрешность включает в себя и погрешность решения прямой задачи численного моделирования /( t ).

Таблица 2

Применение сопряженных уравнений

Параметр	Исходные данные	Полученные значения	Относительная погрешность
Ь0	6 X 10-12	5,468 x 10-12	8,7 %
Е Ь	39,559	39,559	0 %
D 0	4,1 x 10-3	4,104 x 10-3	1,7 %
Ed	37,629	37,629	0 %

На рис. 4, 5 представлены поверхности

G = F²(9) + F²(11) при фиксированных D = D*,

Ь = Ь*. Из рис. 4 видно, что для Ь важно найти хорошее начальное приближение.

Уравнение F = 0 хорошо обусловлено по каждому из параметров модели. Для самого «трудноуловимого» параметра Ь 0 среди указанных значений а(6( Ь 0 ) < 0,3 %) наименьшую погрешность дает а = 9.

Таким образом, изложенные этапы алгоритма параметрической идентификации позволяют восстановить параметры модели с относительной погрешностью, которая с запасом «поглощается» точностью ТДС-эксперимента. В предлагаемой итерационной процедуре оценивания используется подсчет интегралов по времени, а не численное решение краевой задачи при текущих приближениях параметров. Входные данные /( t ) используются под знаком интеграла, что обеспечивает определенную помехоустойчивость. Если мембрану нельзя считать тонкой (это зависит от материала и условий эксперимента), целесообразно взять ф(х) = С-А 0 [х -1 0 ]² k , к >  1.

Работа выполнена при поддержке РФФИ (грант 09-01-00439).

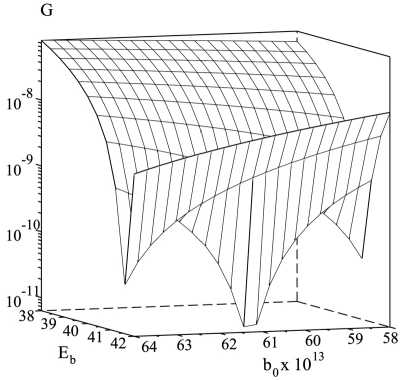
Рис. 4. Экстремум G ( b )

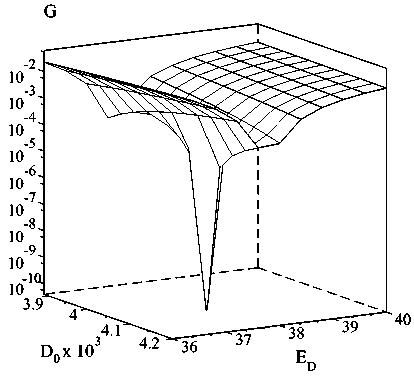
Рис. 5. Экстремум G ( D )