Параметрическая идентификация обобщенной модели Номото с помощью аппарата вариационного исчисления

Параметрическая идентификация модели является сложной математическо й задачей ( Эльсгольц , 1969; Моисеев , 1979), которая может быть решена с помощью современной вычислительной техники.

Проблема идентификации параметров обобщенной модели Номото посредством разложения решений в ряды Фурье рассмотрена в статье ( Пашенцев , 2010). Другой подход к идентификации предложен нами в работе ( Yudin et al. , 2014), где решена задача идентификации простейшей модели Номото для циркуляции судна. В настоящей статье предлагается вариационное решение задачи идентификации для обобщенного уравнения Номото ( Nomoto et al. , 1957) с использованием данных, полученных в ходе наиболее информативного стандартного испытания при выполнении маневра "зигзаг".

Дифференциальное уравнение, рекомендованное 14-й Международной конференцией опытовых бассейнов для решения проблемы управляемости ( Соболев , 1976), определяет криволинейное движение судна и имеет вид

T p^ + T s^ + ® + ^Н + v to- = K s + K s T 3 T ,                  (1)

tt                                                     t где ω – угловая скорость поворота судна; δ – угол кладки руля; параметры Тp, Тs, T3, Kδ, ν1, ν2 подлежат идентификации по результатам натурных испытаний.

В дальнейшем будем оперировать уравнениями 1-го порядка; введем обозначения: Е = d ω / dt – угловое ускорение судна; К – курс судна. Используем простое дифференциальное соотношение ω = dК / dt . Таким образом, для описания рассматриваемого движения вместо уравнения (1) имеем следующую систему дифференциальных уравнений 1-го порядка:

dE      d ω d δ

— = (-Ts — - to - V1® to - v2® + K5S + KsT3 —) / Tp, dt        dt                                  dt dω dt

dK

dt

= ω.

Такое представление задачи дает возможность решать ее в вычислительной среде MathCad. Минимизируем следующий функционал:

min{ ∫ [ α ( K – K ^э)² + ( ω – ω ^э)²] dt } = min{ ∫ Fdt },

т.е. потребуем от модели максимальной адекватности экспериментальным данным по углу поворота судна и угловой скорости вращения. Интеграл (3) используем на интервале (0, t f ). В качестве весового коэффициента выберем множитель α = (1 / t f )², делающий слагаемые однородными и равнозначными. Уравнение Эйлера – Лагранжа для экстремали в этом случае выглядит так:

Агарков С.А., Пашенцев С.В. Параметрическая идентификация… дF  d ( дF )

д Х dt (д Х ’)

д F  d (д F )

д K dt (д ю )

=2а( K - K э) -—(2(ю - юэ)) = 0, dt что дает в итоге

а( K - K3) - — + — = 0.(4)

dt dt

Если учесть, что d го / dt = d ² К / dt ², то получим дифференциальное уравнение 2-го порядка относительно угла поворота курса судна К на экстремали:

d2 K—Ю

—-— аК = аК +--= ^(t ).

dt2

Это уравнение решается известным образом; его общее решение записывается в форме

К (t) = E1 (t) e /4 + E2 (t) e - t / tf, где E1(t) и E2(t) находятся методом вариации констант в виде интегралов: tftf

E 1 (t ) = j у( t ) e ^tltf dt , E ₂ ( t ) = j y( t ) et^tf dt . 0                              0

В нашем случае можно также получить экстремаль в виде дифференциального уравнения 1 -го порядка относительно угловой скорости судна го . Подставим в уравнение (4) значение производной угловой скорости из уравнения (2), продифференцируем получившееся уравнение по времени и в него вновь введем значение производной угловой скорости. Получим нелинейное дифференциальное уравнение 1-го порядка относительно угловой скорости поворота на экстремали:

- а(ю - К ^э) - ю^э + ( - Т --ю - v ю|ю| - v ю³ + K g§ + K^3 —) / Тр = 0*      (5)

s dt                                      dt р

Затем можно предпринять попытку идентифицировать параметры нашей модели. Перепишем уравнение (5) как линейное уравнение относительно параметров модели:

(а(ю — K ^э) + ю^э ) 7 р + T s Ю + У 1 ю|ю| + v ю³ — K § 8 — K § 7 3 8 = —ю.                 (6)

Для этого следует иметь шесть условий, поскольку модель содержит шесть констант. С учетом начального условия на левом конце интервала интегрирования [ го (0) = 0, го '(0) = 0 и 8(0) = 0] можно получить только одно алгебраическое уравнение, связывающее искомые константы:

аK ³ (0) - Ю ³ (0) + K ₅ Т з / Т р ^ = 0.

dt

На правом конце интервала интегрирования t = tf должно выполняться естественное граничное условие:

д F д.х'

— = 2(ю - ю ³ ) = 0. д ю

Откуда получим

®( t f- ) = ®^э( t f ).

Следовательно, необходимо набрать еще четыре условия для замыкания задачи идентификации. Зададим условия в промежуточных точках маневрирования. Тем самым из всех возможных экстремалей многопараметрического семейства выберем ту единственную экстремаль, которая пройдет через заданные точки в пространстве состояний модели. Вычислительные процедуры опишем ниже в процессе численного решения конкретной задачи идентификации.

2.    Численное решение

Рассмотрим численный пример использования этого подхода аналогично тому, как это было сделано при решении более простых задач разгона и циркуляции судна ( Yudin et al. , 2014). Результаты натурных испытаний типа "зигзаг", как правило, слишком "зашумлены" погрешностями различного генезиса. Поэтому в качестве опытных данных используем результаты моделирования маневра "зигзаг 10/10" танкера "Саратов" (в балласте). Параметры математической модели указаны в таблице.

т T p	Т s	V 1	V 2	K 5	T 3
291	11	-133	6815	0.0285	0.114

Вестник МГТУ, том 18, № 1, 2015 г.    стр. 7-11

Данные параметры были получены при решении задачи идентификации обобщенного уравнения Номото посредством разложения уравнения движения в ряд Фурье ( Пашенцев , 2010).

Результаты такого моделирования представлены на рис. 1: курс судна, угловая скорость поворота и кладка руля показаны как функции времени.

время в сек

Кладка руля del

Курс К

Утл. скорость Ош

Рис. 1. Изменение характеристик движения судна при испытаниях "зигзаг 10/10"

В качестве дополнительных десяти точек возьмем характеристики движения, достигающие экстремальных или нулевых значений (рис. 1). Набор значений характеристик, полученных с помощью режима трассировки в системе MathCad, представлен на рис. 2. Вектор Т определяет моменты времени, в которые требуется совпадение характеристик состояния модели и результатов испытания; вектор В – правые части уравнения (6), матрица А содержит коэффициенты при искомых параметрах модели в том же уравнении. При этом система десяти линейных уравнений записывается в матричной форме:

A X = B , где Х – вектор искомых параметров.

' 5 \ 50 54 141 т , 14 в= /wv 25? 328 350 121 (232J		1	А =		1	2	з|	4	5
	1	-1.693-W-5		1	8.385'10-6	1.266-Ю"5	2.В67-10"1”	4.854-Ю"15	-0.175
	2	-8.201 "Ю"3		2	-1.132'10-6	2.14'104	6.725-IO"5	5.515-Ю"7	-0.131
	3	-9.ОО2-10-3		3	-1.385'Ю"5	1.835'104	8.103 "IO-5	7.294-Ю"7	0.044
	4	0.015		4	1.373-IO"5	-7.105-Ю"5	-2.Й-Ю4	-3.465-Ю^	0.175
	5	0.015		5	1.33'КГ5	7.671-Ю"5	-2.248-104	-З.Э7-Ю"6	0.044
	б	-0.014		6	-1.562-Ю"5	-1.773'104	2.055'104	2.945-Ю"6	0.044
	7	0.016		7	1.737-Ю"5	-7.433-Ю-5	-2.4Й-104	-3.884-ЮГб	0.175
	8	0.014		8	$736 10-5	2.643'104	-1.866-104	-2.548-10-6	-0.175
	9	0.011		9	7.6'10-6	-2.957-104	-1.288-104	-1.463-10-6	0.175
	10	-0.016		10	-1.762-Ю"5	8.2110-5	2.4Й-104	3.889-10-6

Рис. 2. Исходные данные, используемые для определения параметров модели

Данные значения характеристик состояния объекта (угловая скорость, курс, угол кладки руля) выберем в качестве экспериментальных (они нами наблюдаемы). При этом учтем, что в условиях натурного эксперимента обычно не наблюдаются значения производных курса и угловой скорости, которые необходимы для подстановки в уравнения (5) и (6). Их найдем с помощью конечных разностей по традиционным формулам. Следует отметить, что на рис. 2 приведено избыточное количество данных для однозначного решения задачи. Это обстоятельство предоставляет возможность решить задачу определения параметров как переопределенную и получить бóльшую устойчивость решения.

Дальнейшее решение можно осуществить с помощью MathCad двумя способами. Использование встроенной функции lsolve дает решение немедленно (рис. 3, скриншот экрана).

' 194.713 ' 4.98

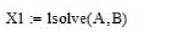
-136.178

6.112 х 10

0.016

^ -0.028 ,

Рис. 3. Решение переопределенной системы с помощью встроенной функции lsolve

Агарков С.А., Пашенцев С.В. Параметрическая идентификация…

Другое решение требует определения для матрицы А псевдообратной матрицы Арр (рис. 4).

^vRR-/

	117393	< 291 x
	1.409
		11
(at-a) at	-137.677	-133
x =	,        3                           th >
	5.571 x 10                            *	6815
Арр - В
	8.48 x 10“ 3	0.0285
	< -0.02 „	< 0.114

Рис. 4. Решение переопределенной системы с помощью псевдообратной матрицы Арр

Решения Х ₁ и Х получились совершенно одинаковыми, значит, функция lsolve использует псевдообратную матрицу. На рис. 4 приведен также вектор параметров, которые послужили базой для получения опытных данных в модели Номото.

Наконец, можно максимально переопределить задачу и использовать весь комплекс измерений кинематических параметров с номерами от 1 до 500 (500 с – длительность эксперимента, рис. 1). В данном случае естественно применить метод наименьших квадратов (МНК) и получить матрицу А при искомых параметрах и вектор правой части В. Для нашей системы уравнений формальное применение МНК состоит в умножении уравнения (6) в точке с номером k последовательно на ω′′, ω′, ω|ω|, ω3, δ, δ′, вычисленные также в точке с номером k, затем в сложении по всем экспериментальным точкам. Получим так называемую нормальную систему шести уравнений с шестью неизвестными, решение которой проводим обычным образом, демонстрируя его в виде фрагмента решения в среде MathCad (рис. 5). Чтобы отличить данное решение от предыдущих, введем обозначения: С – матрица системы; D – вектор свободных частей. Оба решения (прямое и полученное с помощью псевдообратной матрицы) практически совпадают. Как и ожидалось, результат ближе к параметрам модели, использованной для генерации экспериментальных данных.

		r 240345	240.035 '		< 291
Cpp :=	(cT c) * cT	8.177	8.176		11
XI,	= Cpp • D	-135.723 XI =          -          x2 = 6.572 x 10^	-136.03 J 6.583 x 10	4’ :=	-133 6815
X2	-C-* D	0.023	0.023		0.0285
		-0.037	L -0.036 J		.0.114

Рис. 5. Решение системы нормальных уравнений методом наименьших квадратов

3.    Выводы

Предложен вариационный подход к решению задач параметрической идентификации математических моделей. При моделировании с учетом малого числа параметров такой подход способствует получению достаточно точных результатов ( Yudin et al. , 2014) и может быть использован для аппроксимации сложных движений набором простейших движений, модели которых легко идентифицируются. В настоящей статье такой подход был применен к модели с большим числом идентифицируемых параметров и дал вполне удовлетворительный по точности результат. Наилучший результат идентификации получен при использовании всех исходных данных модельного эксперимента, т.е. при двойном отборе идентифицируемых параметров – с помощью вариационного уравнения и метода наименьших квадратов.