Параметрическая идентификация распределительной сети в составе АСКУЭ

В целях комплексной автоматизации и информатизации процессов энергопотребления в распределительных электрических сетях (РЭС) в настоящее время широкое применение находят автоматизированные системы контроля и учета электроэнергии (АСКУЭ) [1], в которых в основном выполняются функции измерения данных с электронных счетчиков, установленных у абонентов трехфазной сети, и коммерческого учета электроэнергии. В этих автоматизированных системах практически не решаются задачи, направленные на повышение технико-экономических показателей распределительных компаний. К ним, в частности, относятся задачи оперативного мониторинга потерь электроэнергии [2–4], диагностики функционального состояния [5–7] и оптимизации режимов работы распределительной сети [8–11], решение которых позволяет существенно сократить потери и повысить качество электроэнергии. Анализ показывает, что решение указанного комплекса дополнительных функциональных задач АСКУЭ связано с разработкой соответствующих математических моделей и методов расчёта трёхфазных сетей в режиме реального времени, что связано с определёнными трудностями [12–15]. Последние, в частности, связаны с такими факторами, как несим- метрия токов и напряжений [4, 11, 16], параметрические неопределенности [6], связанные с «дрейфом» сопротивлений межабонентских участков магистральной линии, значения которых зависят от ряда условий (климатических, временных). В связи с этим в статье развивается подход к идентификации параметров (сопротивлений) РЭС, предложенный в [4, 17], с учетом фактора несим-метрии токов и напряжений в режиме реального времени. При этом рассматривается общий случай, когда фазные и нейтральный провода имеют разные сечения. Анализ показывает, что полученные результаты параметрической идентификации позволяют в ряде случаев упростить решение указанного выше комплекса задач в составе АСКУЭ.

Постановка задачи

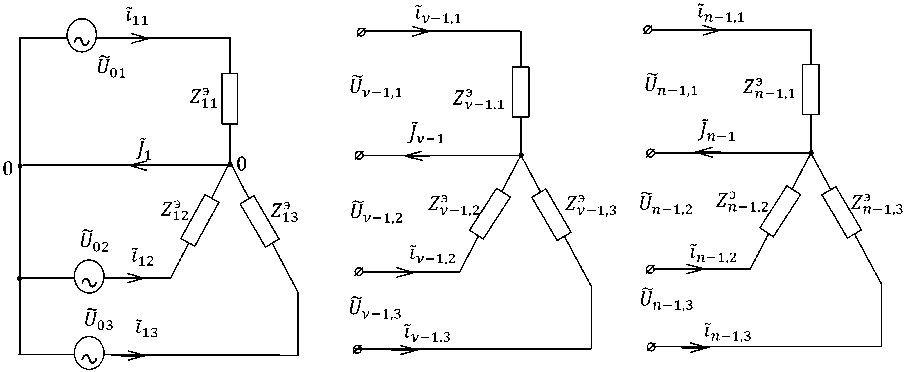
Рассмотрим четырёхпроводную трёхфазную распределительную сеть напряжением 0,4 кВ, расчётная схема которой показана на рис. 1, где для удобства дальнейших математических операций через индексную переменную к (к = 1,3) указаны соответственно фазы А, В и С, а через ν – номера электрических контуров сети.

Остальные обозначения следующие: Z_vk - сопротивление электроприёмника (нагрузки) сети с координатой ( v , к), подключённого к фазе с номе-

Рис. 1. Расчетная схема трехфазной сети

ром к; /_vk, U_vk - мгновенные ток и напряжение на нагрузке Z_vk ; i_vk,Z_vk - мгновенный ток и сопротивление ν -го межабонентского участка (МАУ) к-й фазы; H_vk , й- у - напряжения соответственно на у -м МАУ к-й фазы и нейтрального провода; J_v , Z_v - мгновенный ток и сопротивление ν -го участка нейтрального провода; U_ok, /_ok = i_lk - мгновенные напряжения и токи на входах соответствующих фаз.

В каждый момент времени t Е [t ^ , t ^ ₊₁] сумма полезных токов I_k(t), потребляемых абонентами сети в соответствующих фазах, определяется как

4(0 = y"=1ivk(t), к = 13.

Далее примем следующие предположения:

• 1.    Трехфазная сеть функционирует в нормальном (штатном) режиме, т. е. выполняются следующие условия:

• 2.    В сети существует несимметрия токов и напряжений.

• 3.    Линейные и нейтральный провода сети имеют различные сечения и для сопротивлений МАУ выполняются следующие условия:

• 4.    В системе используются технические средства для подавления высших гармонических составляющих токов и напряжений в сети.

• 5.    В базу данных АСКУЭ в каждом интервале наблюдения [t ^ , t ^ ₊₁] (где ^ = 1,2, 3,...) поступают следующие данные:

^|Ik ^{- I}0k | ^ ^д/тах , ^к = ^1,3 , (1) где I_k , I_ok - действующие значения соответственно полезного тока I_k и входного тока к -й фазы I_ok , измеряемого счетчиком на выходе ТП; Д/_тах -максимально допустимая погрешность измерения токов в сети.

Zvk * zv, к = 1,3,

Z v1 * Z v2 , Z vi * z_v3, Z_v2 * Z_v3. (2)

• •    действующие токи I_vk и напряжения U_vk на нагрузках Z_vk , у = 1,п, к = 1,3;

• •    коэффициенты мощности cos ф_vk, у = 1,п, —

к = 1,3.

Введём матрицу Z и вектор Z_o, элементы которых состоят из сопротивлений Z_vk и Z_v в текущем интервале наблюдения [t ^ , t ^ ₊₁]:

Z11

Z = lZ12

L Z13

Zn1

Zn2

Zn3

], ^Z0 = [ ^Z1 , ^Z2 ,

^Zn^{] .}

Требуется определить оценки элементов матрицы Z и вектора Z_o с использованием данных, поступающих в интервале наблюдения [t ^ , t ^ ₊₁] в базу данных АСКУЭ.

Решение задачи

Необходимо отметить, что на основе исходных данных, поступающих со счетчиков электроэнергии, невозможно оценить текущее электрическое состояние трехфазной сети. Для этой цели необходимо предварительно идентифицировать модели нагрузок, описывающие динамику синусоидальных токов и напряжений на нагрузках сети. Как известно, в установившемся режиме эти переменные можно представить в комплексной форме [18]:

I vk = /^ k +)I"k = W^ ,

U vk = U v^Bk +;U_v ^Mk = U vk e V* v_k ,              (3)

V = 133, к = 1,3, где символы «в» и «м» обозначают вещественные и мнимые части соответствующих комплексных переменных; Ivk, Uvk, avk, фvk — модули и фазовые сдвиги этих переменных. При этом

• a vk = a vk — a vk , Ф vk = $ vk - Ф Vk , к = 1,3,

avk = 2(к — 1) n/3, ФVk = 2(к — 1) n/3, где avk, фvk - приращения фазовых сдвигов относительно их номинальных значений avk и фVk, обусловленные несимметрией токов и напряжений в сети. Таким образом, для того чтобы модели нагрузок представить в форме (3), необходимо найти неизвестные величины ccvk и ^vk по данным, по-

лученным со счетчиков электроэнергии и хранящимся в базе данных АСКУЭ. Один из методов решения этой задачи предложен в [4]. В случае, когда построена модель нагрузок в форме (3), на основе первого закона Кирхгофа можно вычислить межабонентские токи ivk и /v по следующим фор-

мулам:

ловия (2) для сопротивлений МАУ. В качестве исходных данных будем использовать напряжения U_vk на нагрузках сети и межабонентские токи ^_vk ^и Л, которые являются известными величинами и определяются соответственно по формулам (3), (4) и (5). Рассмотрим интервал наблюдения [t ^ , t ^ _+l], в котором трехфазная сеть находится в нормальном состоянии, т. е. выполняются условия (1). При этом, начиная с начальных контуров (v = n) сети (см. рис. 1), для каждого v (v = 1,n — 1) после-

ivk = ^T=viik = ^T=v(iTk+jirky---------- _          -------- v = 1,n; k = 1,3,                           (4)

Zv     ^ vl + ^ v2 + ^ v3 ; ^.

— v = 1,n.                                    (5)

Для дальнейших построений будем использовать второй закон Кирхгофа, описывающий баланс напряжений в v -х контурах сети (см. рис. 1):

^vk + Йу + ^vk - Uv-i,k = 0, v = 1,n, k = 1,3.                            (6)

На основе закона Ома соотношения (6) можно представить в виде следующей системы линейных уравнений относительно искомых пара-

дующие части сети заменяем эквивалентными сопротивлениями Z v _k (v = 1,n — 1, k = 1,3), значения которых можно вычислить. Схемы, иллюстрирующие эту процедуру, приведены на рис. 2.

Например, для трехфазной сети, образованной всеми ее электрическими контурами (рис. 2а), со-

ответствующие эквивалентные комплексные со-

метров z_vk и z_v :

^ vl ^ vl ^{+ J}v^zv   ^bvl ,

противления определяются как

ZЭk = Uok/ilk, k = 1,3, а для части сети, образованной, начиная с v-го контура (рис. 2, б), и для конечного контура (рис. 2, в) они соответственно вычисляются по следующим формулам:

z vk = U_V k /i vk , v = 17Й, k = 13,

^Zn-l,k = ^ n-l,k / ^ln-l,k , ^k = 1, ³ -              ⁽⁸⁾

С другой стороны, для Z v _-l , _k справедливы

^ v2^zv2 ^{+ J}v^zv   ^bv2 ,

следующие выражения:

^ v3^zv3 ^{+ J}v^zv   ^bv3 , ^v    1, ⁿ ,

где b vk = ^ v-i,k - U vk (k = 1,3).

Как видно из соотношений (7), для каждого v -го контура имеем три уравнения (k = 1,3), а количество неизвестных параметров (z_vl, z_v2, z_v3, z_v ) равно 4. Поэтому для оценки искомых параметров необходимо найти дополнительные условия, которые совместно с уравнениями (7) позволяли бы осуществлять их идентификацию.

В целях идентификации элементов матрицы Z и вектора Z_o будем считать, что выполняются ус-

7 ^э . , ^Zv-l,k

(Z yk +Z y +^ v^- Z y-i^ ⁽Z y_k ^+Z y ^Vk ) ^+Z y- i,k

v = 1,n — 1,k = 1,3, (9) где эквивалентные сопротивления Z v _k вычисляются по формулам (8), а сопротив лен ия электроприемников Z_vk = U_vk/I_vk , где v = 1,n, k = 1,3.

Так как эквивалентные сопротивления Z ^ _k конечных участков РЭС определяются сопротивлениями электроприемников (Z ^ _k = Z_nk), которые

являются известными величинами, то для каждого электрического контура трехфазной сети на основе

а)

в)

Рис. 2. Схемы оценки эквивалентных сопротивлений Z^_k

соотношений (9) можно получить следующие линейные алгебраические уравнения относительно

искомых параметров z_vk и z_v:

4 О ^zvk + ^zv    ^fvk , ^   1, ⁿ , ^к 1,3,          ⁽¹⁰⁾

где f_vk — известные величины, которые определя-

ются по следующим формулам:

fvk —

^zvk^(zv-i,k Z v-i.k^ Z v-i^v-i.k

z³ v-ik^-zv-ik

Для определения искомых параметров на основе соотношений (5) и (7) запишем следующие систе-

мы уравнений:

V^k+jyZv= bVk, к =13^(11)

^ Vl ^ VZ ^- V3

— + — + — — 7v,v = 1,n.(12)

ZVl ZV2

Теперь из соотношений (10) определяем zvl, zv2, zv3, а из равенств (11) - uvl, uv2, uv3. Путем подстановки полученных выражений в (12) получаем

следующие соотношения:

^ Vl^— j v^ZV f vl^-Zv

+

b v2^- i v^zv f v2^-ZV

I b v3^- i v^zv f v3^-ZV

= Jv,v = 1,n. (13)

Отсюда после несложных преобразований по-

лучаем следующие кубические алгебраические

уравнения относительно параметров z_v :

a₃z V + a₂z V + a_lz_v + a₀ — 0,v = 1, n, (14) где a₀, a_l, a₂, a₃ - коэффициенты, которые вычисляются на основе соответствующих преобразований соотношений (13) и имеют следующий вид:

^a0 — ^fv2^fv3(k _v i ^J _v ^fvl ) ⁺

+fvl(bV2fv3 + bv3 fV2),

^ l ^{— J}v [ ^fv3 (f vl ^{+ f}V2 ) ^{+ f}Vl^fV2 - ^fV2^fV3 ^-

-fvlfv3 - fVlfV2] - bVl(fV2 + fv3) -

-bv2(fvl+fv3)-bV3(fvl+fv2),

a2 — bvl + bv2 + bv3 + 3jv(fvl + fv2 + fv3),

« 3 = -2J v .

Решение уравнений (14) можно найти методом Кардано [19] или на основе использования численных методов [20]. Остальные параметры сети z_vk на основе соотношений (10) определяются по формулам

zvk = fvk -zv, v — 1,n, к — 13.

Таким образом, изложенная выше вычислительная схема позволяет идентифицировать элементы матрицы Z и вектора Z₀, которые записываются в базу данных АСКУЭ и используются для решения дополнительных функциональных задач автоматизированной системы.

Заключение

Предложен метод идентификации параметров (сопротивлений) межабонентских участков распределительной сети напряжением 0,4 кВ по данным АСКУЭ. Считается, что трехфазная сеть функционирует в условиях несимметрии токов и напряжений, а также неконтролируемого «дрейфа» сопротивлений, обусловленного внешними факторами. При этом рассматривается общий случай, когда фазные и нейтральный провода имеют разные сечения. Метод основан на модели нагрузок в комплексной форме, позволяющей осуществить

оценку неизмеряемых и неконтролируемых переменных (токов и напряжений), характеризующих текущее электрическое состояние межабонентских участков магистральной линии. В целях идентификации получены аналитические условия в виде алгебраических уравнений, решение которых дает искомые параметры трехфазной сети. Полученные результаты можно использовать для моделирования физических процессов в электрической системе, а также для решения задач оперативного мониторинга потерь электроэнергии и диагностики состояний функциональных элементов распределительной сети в составе АСКУЭ.