Параметрическая модуляция излучения, отраженного от полупроводника

В настоящее время наметились перспективы создания коротких ИК импульсов с управляемой амплитудно-фазовой модуляцией. Один из механизмов такого управления связан с дополнительным воздействием на полупроводник переменных электромагнитных полей. При этом характер зависимости частоты столкновений свободных носителей v от эффективной температуры электронов Tg обеспечивает существование бистабильных состояний полупроводника с различными Tg [1,2]. В данной работе исследуются возможности генерации динамического профиля Т и вытекающей отсюда е модуляции во времени параметров отраженных от полупроводника сигналов.

Рассмотрим полупроводник в переменном электрическом поле Е = Eo(t)-cos Dtz создаваемом греющим током. Тогда в рамках элементарной теории полупроводниковой плазмы свободных носителей имеем [2-4]:

jk • ^ = 6-v|k -СТо-Те) ♦ e-E-v;

CD

m* • (•gy ♦ vv) = e-E.

При этом эволюция электронной температуры определяется частотами столкновений v с тяжелыми частицами, средней долей энергии б, теряемой за одно столкновение, а также джоулевым теплом eEvz где v - средняя скорость дрейфа носителей, имеющих массу ш*. Температуру тяжелых частиц То будем считать постоянной, зависимости v(Te> и 6(Те> - алгебраическими, характерные времена изменения амплитуды EQ(t> и температуры T^tt) - порядка времен релаксации энергии 1/(6*v)«

Пусть частота греющего поля достаточно велика: Q » б-v. Тогда из (1) с точ-ностью до членов порядка тах(б, ) от оставленных можно получить уравнение, описывающее эволюцию безразмерной температуры

е

о •

где

df ₌ dr

т

о и

о '

значения частоты

столкновений и

доли теряемой энергии

в невозму-

щенном состоянии

е

т=>;

У (f)

D С f )

6/б0;

х = Q/v_o;

2.Е2 с о

3 • к -Т₀*т*•б₀• Vq

Пусть частоты столкновения электронов обусловлены рассеянием на решетке

1 /                                                                         з/ v = v /1  2 на ионизированных примесях v. = v. /f а так что

Р РО            110»

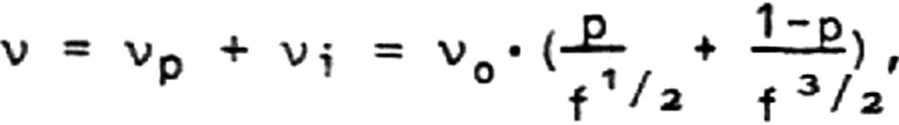
где vA определяется не возмущенными значениями v = v + V. , а р = v /v °                        opoio     po o доля столкновений с решеткой.

т          с                 Р . 1"Р

Таким образом, у = i" + --• f 72 f3/3

Ограничимся далее случаем D = 1, Для низких температур, когда рассеяние на ионах становится определяющим, стационарные решения (2) 1, а = const (т) могут образовать гистерезисную зависимость, подробно исследованную в [l]:

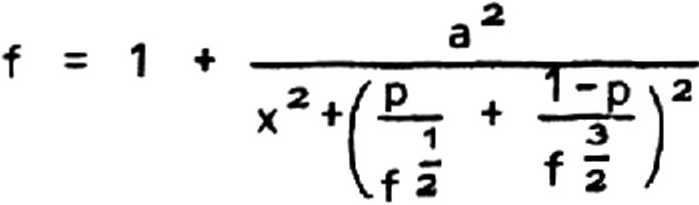
Характерная кривая f (а) изображена на рис. 1. Следует ст                                      2

отметить, что реа-требует небольших

лизация бистабильных состояний возможна при р < р = у и значений х < х (р) (рис. 2>. Данное обстоятельство ограничивает диапазон не сущих частот греющего поля:

6-V « R < v • х (р) . ° ко

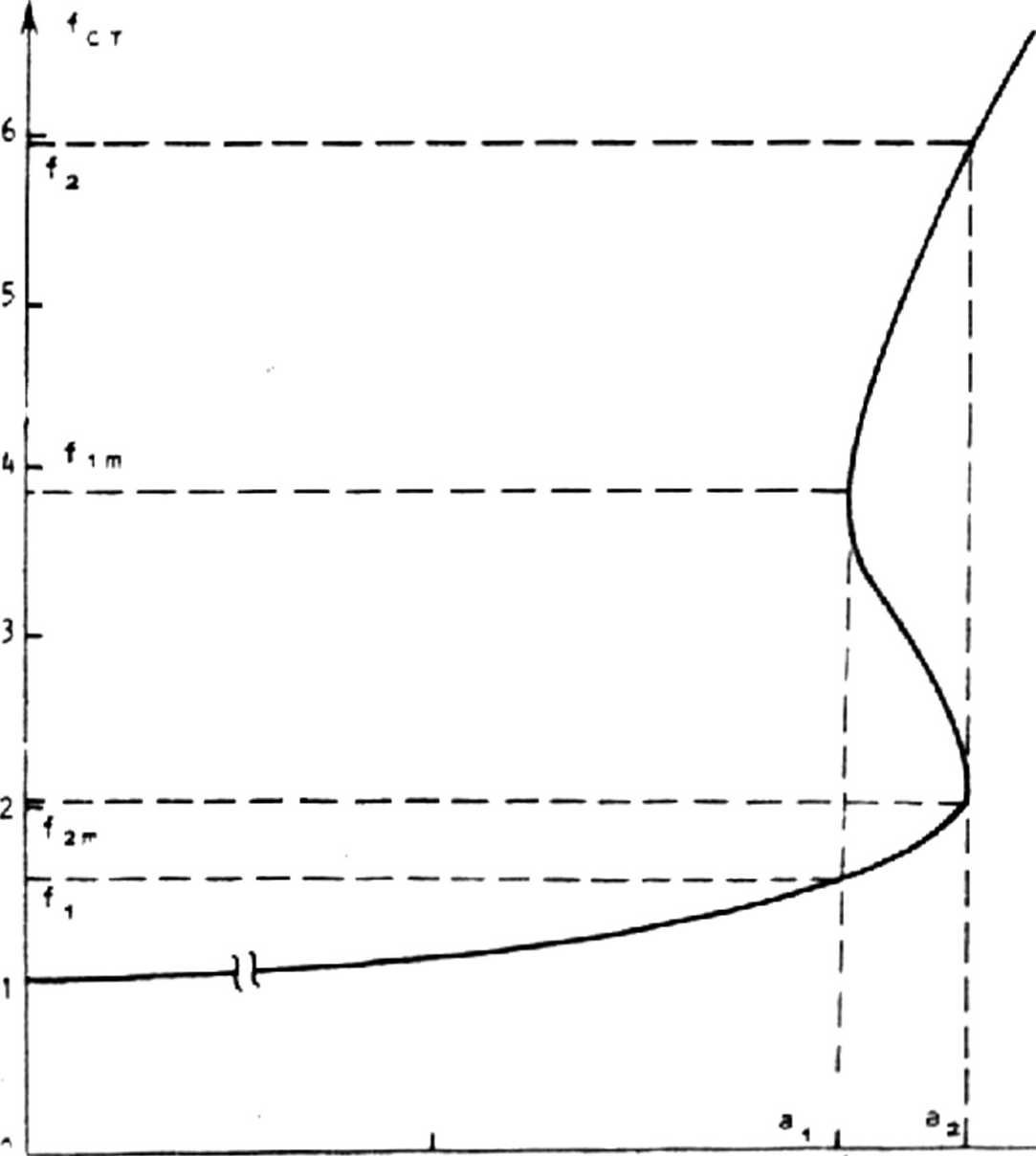
Рис. 1. Бистабильная зависимость fcT(a) для уравнения (3) при р ■ 0,25; х = 0.1^.Характерные точки: а1=0.^^98; а3=0.4бЗб; f1=1.555;

*2=5-975; f,m=3.896; *,„=2.001

Анализ динамического уравнения (2) показывает возможность реализации гар-,                 2пт ионического температурного импульса т = В - C-cos --- .

1 m Требуемый для этого профиль амплитудной модуляции греющего поля а(т) изображен на рис. 3. При этом полагалось тт = 30 и рассматривалась комбинация параметров:

В = 3.765 С » 2.21 х = 0.14 р = 0.25,                                    (4)

обеспечивающая изменение температуры между граничными точками бистабильности (рис. 4, точки 1 и 2) . Интересно отметить, что уменьшение периода т модуляции m температуры f требует увеличения глубины модуляции греющего поля а(т) (см. рис. 3) ♦

0.25

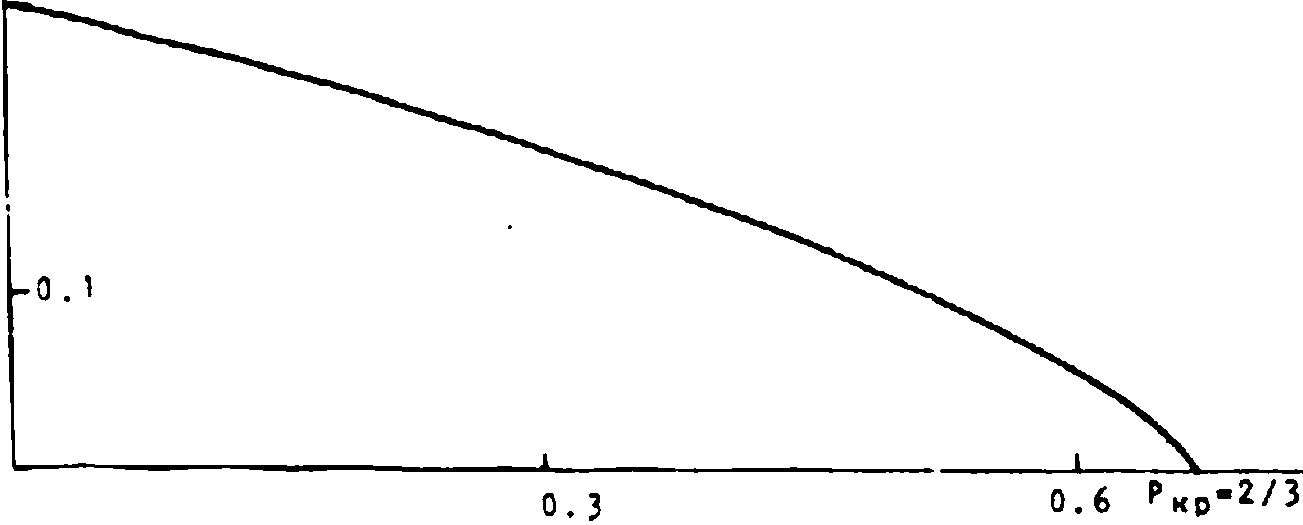
Рис,

Зависимость максимально допустимых х

Ср)

реализующих гистерезисный тип решения (3)

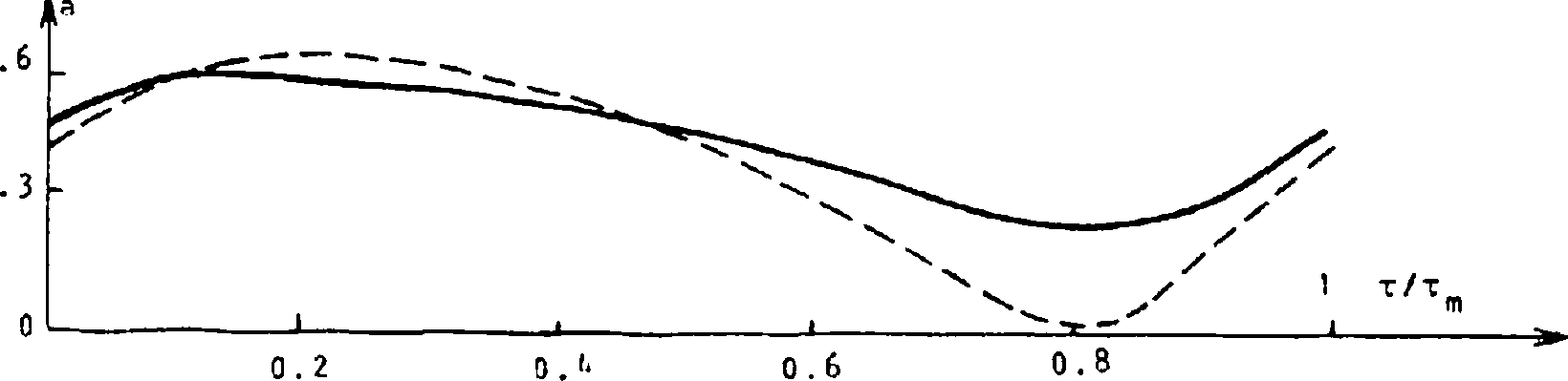
Рис. 3- Гармонический температурный импульс f (т) и требуемый профиль амплитудной модуляции греющего поля а (т) для комбинации параметров (4) при т =22.58 (пунктир) и т =30 (сплошная) m                            m

При этом неравенство а2(т ) > 0 ограничивает минимально допустимые т . В m частности, для рассмотренной комбинации параметров (4) имеем min (г ) = 22.58. Следует также на основании численных экспериментов отметить, что слабо зависит от х. Однако амплитуда а (см. рис. 3) растет с увеличением х. В частно-ГП о X сти, для набора параметров (4) с заменой х = 0.14 на х = 1 (когда кривая f (а) ст имеет не гистерезисный , монотонный характер) атах возрастает в 4-6 раз (для разных т ) . m

Полученные результаты дают возможность управления параметрами волны, отраженной от поверхности полупроводника, температурный профиль которого изображен на рис. 3. Пусть падающее под углом а к нормали s - поляризованное излучение

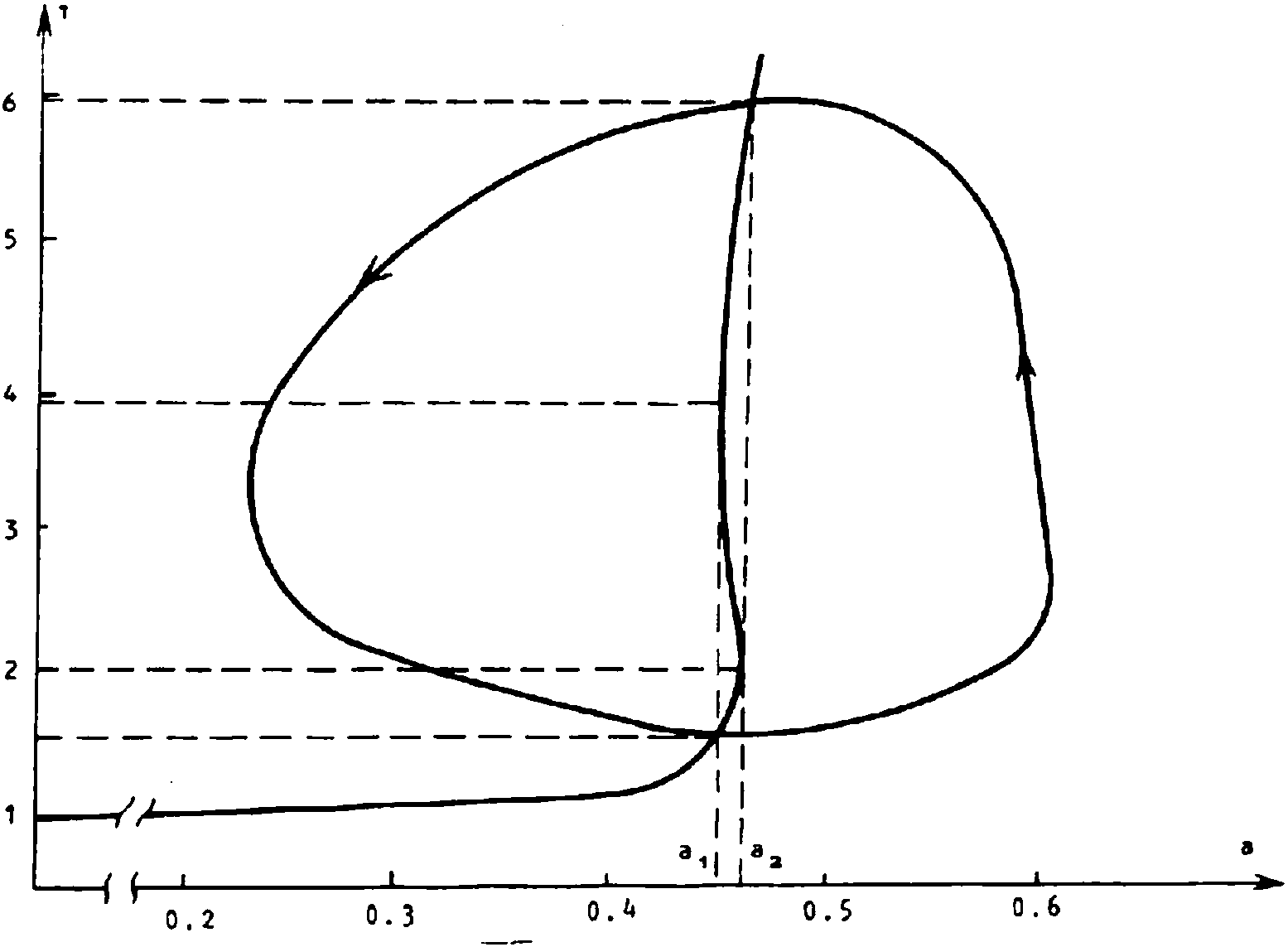
Рис. 4. Диаграмма взаимосвязи функций fСт) и а(т) для комбинации параметров (4) при т =30 (вокруг статической кривой f^^Ca) из рис. 1)

с напряженностью электрического поля

Р F e"1(l)t

^Е ■ Е_о е

имеет частоту ш порядка лэнгмю-

ровской

А2 • N                11

---— = 5.64-10 Е0*т*

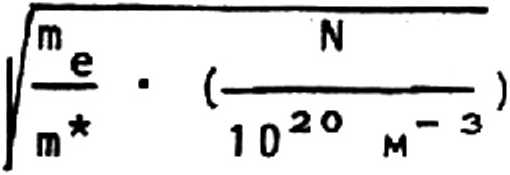
При этом диэлектрическая проницаемость имеет традиционный

вид

[2,4]:

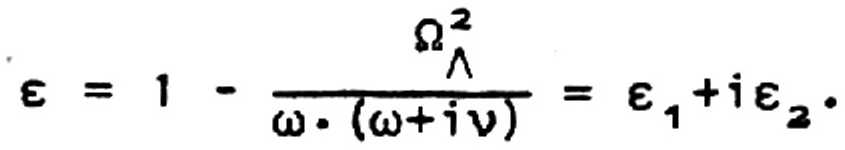
Тогда коэффициент отражения

_ ^{с 0 s 2 а} ~ У^ А ² + е з - 2 i Л- с о s а cos² а + /д²+е² + 2P+-COS а

liil-e^

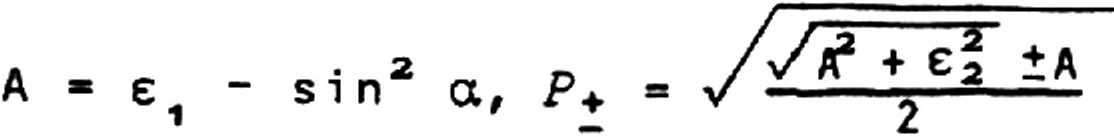
параметрами и = Йд/оо

определяется

е1

2 U

Е

2 и -у

При этом

изменение температуры

v = v/w, а, так как

Т влияет на поглощение v и обеспечивает е

модуляцию отраженной волны, так как v = v0*Y(f), где v0 = v0/u>. Следует отме тить, что оптимизация амплитудной модуляции IRI /IRI .  = max и фазовой max min

Ф__м ~      = max требует различных комбинаций параметров u, v , а. Так, для температурного импульса, соответствующего рис. 3 и р=0.25, имеем: при u=0.8z vQ = 5, а—п/4 амплитудная модуляция отраженного сигнала достаточно глубока

< IR I - /1 RI -   - 3.2), а фазовая незначительна (Ф              ” °-23 рад)

max min                                      max min

(рис. 5). При u = 0.5, v0=2, a = п/4 ситуация обратна (рис. 6).

tn ( р а д . )

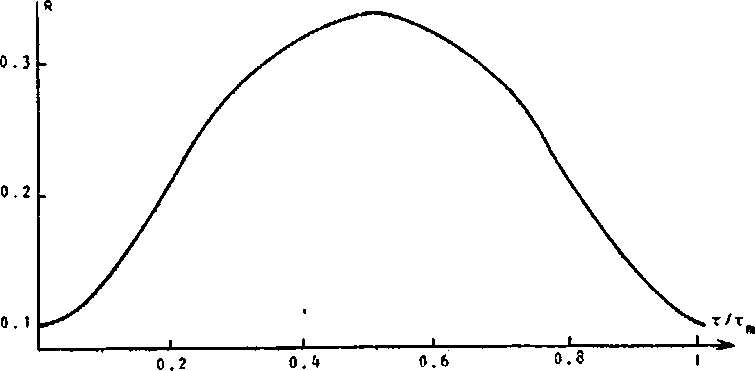
Рис. 5. Характерные амплитудно-фазовые профили при U=0.8; Vo=5; а=п/4

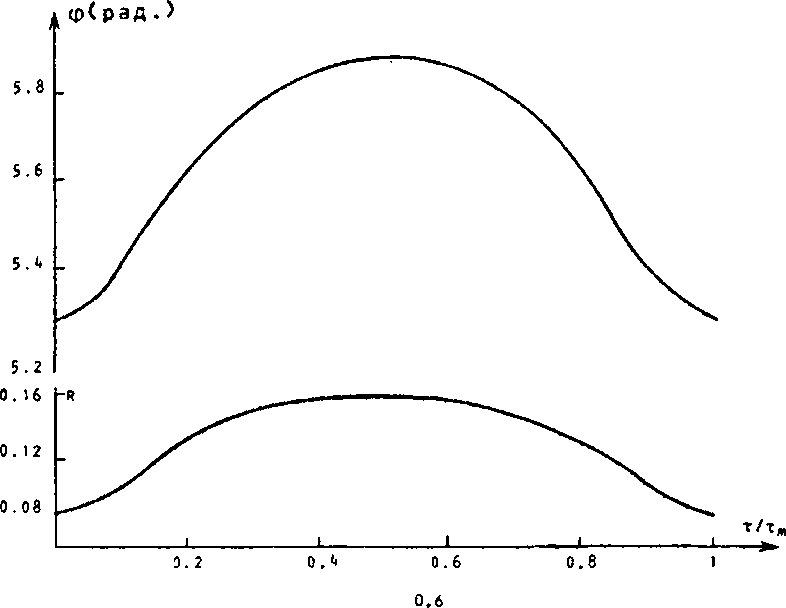
Рис. 6. Характерные амплитудно-фазовые профили при U = 0.5; V_o = 2; o=ti/4