Параметрические модели пульса и перспективы их использования

ПАРАМЕТРИЧЕСКИЕ МОДЕЛИ ПУЛЬСА И ПЕРСПЕКТИВЫ ИХ ИСПОЛЬЗОВАНИЯ

Современная медицина нуждается в разработке и совершенствовании приборов и приборных систем для клинической экспресс-диагностики состояния человека. При этом к числу основных требований, предъявляемых к такой аппаратуре, относятся неинвазивность, простота практического использования и возможность применения при массовых обследованиях населения. Исходя из указанных требований, весьма заманчивой представляется разработка диагностических систем с использованием опыта пульсодиагностик и Китая и Тибета.

Восточные методы диагностики в большинстве случаев дают уникальные результаты, однако широкое их распространение среди врачей, придерживающихся традиционной европейской школы медицины, пока еще затруднено. Трудности в широком распространении методов восточной диагностики, вероятно, состоят в несоответствии медицинских понятий европейской и восточной школ. Кроме того, процесс постановки диагноза восточным лекарем носит существенно субъективный характер и сопровождается большим числом полу-мистических тайн и ритуалов (1 ].

Естественно, что построение приборных систем на такой идеологической базе долгое время считалось абсолютно невозможным. Тем не менее европейская медицинская школа уделяла значительное внимание развитию методов изучения пульсовых колебаний. Благодаря этому современная медицина располагает большим арсеналом технических методов исследования пульса: сфигмография, плетизмография, флебография, реография, фотоплетизмография и другие [2], основанных на объективных физических законах и обеспечивающих повторяемость результатов. При этом реография и фотоплетизмография считаются наиболее перспективными методами исследования пульса [31 и являются областью интенсивных исследований.

Теоретические основы моделирования и схема экспериментальной установки

В основе фотоплетизмографии лежит принцип световой денситометрии, а именно, регистрации изменения оптической плотности живой ткани каждый период сердечного сокращения. Эти изменения основаны на спектральных особенностях гемоглобина. На рис. 1 приведены характерные спектры поглощения оксигемоглобина и восстановленного гемоглобина [41. В диапазоне

Рис. 1. Кривые поглощения света для восстановленного гемоглобина (Ли оксигемоглобина (2)

длин волн 600—700 нм поглощение света восстановленным гемоглобином в несколько раз выше, чем оксигемоглобином, что приводит к значительной разнице в оптической плотности артериальной и венозной крови. В то же время существует ряд так называемых изо-бестических точек (длин волн), в которых поглощение света оксигемоглобином и восстановленным гемоглобином одинаково.

Использование источника света с длиной волны, равной изобе-стической, дает возможность путем измерения изменения оптической плотности ткани зарегистрировать объемный пульс, т. е. разницу между артериальным при током и венозным оттоком на протяжении одного сердечного цикла, когда венозный отток постоянен.

С практической точки зрения наиболее подходящей для этой цели оказывается изобестическая точка А ■ 805 нм, хотя хорошие результаты можно получить и вне изобестической точки, например, в диапазоне X = 900 + 930 нм, где поглощение света оксигемоглобином и восстановленным гемоглобином.

во-первых, мало, а во-вторых, мало отличается друг от друга.

Для целей и регистрации кривой пульса используются оптические системы, работающие как на проходящем, так и на отраженном свете, что практически не влияет на форму переменной составляющей получаемого сигнала. Типичные формы регистрируемых фотоплетизмосигналов для пожилых и молодых пациентов приведены на рис. 2. В настоящее время распространено мнение, что частота и продолжительность пульсовых волн зависит от работы Жца, а форма — от состояния периферических сосудов. Кроме того, высота много пульса зависит от силы сокращения миокарда, сопротивления периферических сосудов, вязкости крови.

Значительное влияние на форму регистрируемой кривой может оказать сила прижима датчика к коже. В качестве оптимального давления для установок с проходящим светом рекомендовано 0.5-1.0 (5-10) и 2-4 кПа (20-40 мм рт.ст.) для установок, работающих на отраженном свете (5].

Типовой подход к анализу записанной фотоплетизмограммы состоит в выделении волн первого, второго и третьего порядка, а также ряда характерных точек на кривой и расчету по ним амплитудных, временных и амлитудно-временных показателей [6]. Общее число рекомендованных показателей у исследователей различно и иногда превышает двадцать.

На практике большой набор параметров, сложным образом связанных между собой, вызывает трудности в принятии диагностических решений. Кроме того, наличие физиологического разброса значений параметров не позволяет сформировать жесткие границы, используемые при решении задач типизации, что усложняет процесс формализации поставленной задачи.

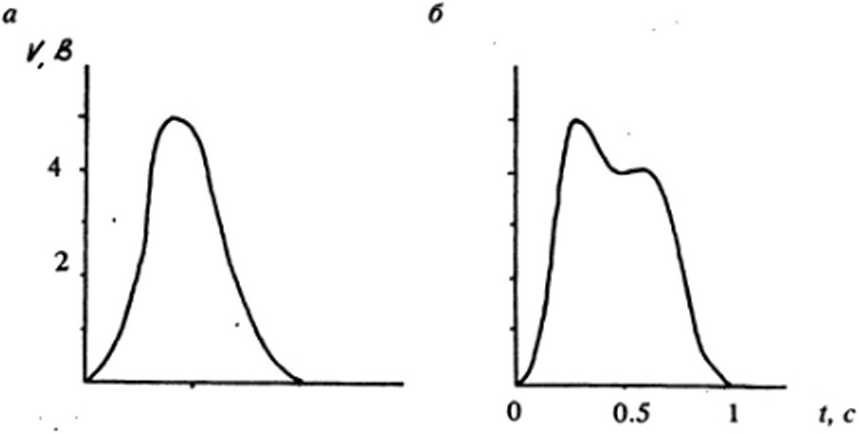
Рис. 2. Типовые формы фотоплетизмосигналов (после усиления): о — для пожилых пациентов; б — для молодых

Не отвергая традиционный подход к анализу фотоплетизмограмм, автором была предпринята попытка моделирования пульсовых сигналов с помощью хорошо зарекомендовавших себя в технической кибернетике методов идентификации динамических сигналов и систем.

Схема использованной экспериментальной установки приведена на рис. 3. В качестве источника света использовались широко выпускаемые промышленностью инфракрасные диоды с Л - 920 нм. Все исследования проводились на отраженном свете с датчиком пульса, устанавливаемом на кончике пальца. После дискретизации во времени с задаваемой частотой/о данные вводились в ЭВМ, где и проводилась их обработка.

Моделирование сигнала осуществлялось на основе широко известной концепции формирующего фильтра, согласно которой наблюдаемый процесс рассматривается как результат прохождения белого шума через некий формирующий фильтр. В общем случае дискретный стационарный процесс с нулевым средним и конечной дисперсией согласно теореме о декомпозиции Вольда может быть представлен в виде где {<*(/)} - дискретный белый гауссов шум с нулевые средним; bk - коэффициент 00

формирующего фильтра, 2 ^ < »; {ХО}” наблюдаемый дискретный процесс; 4=0

t - дискретный отсчет времени.

Модель (1) может быть записана и иначе, как взвешенная сумма прошлых наблюдений сигнала

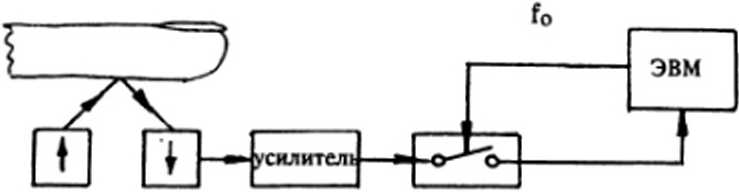
Рис. 3. Упрощенная схема экспериментальной установки

Х0 = ” 2 а_к>4=Ю

где а_к - параметр модели.

Понятно, что для практического использования модели (1) и (2) малопригодны, так как содержат бесконечное число членов. Переходя к конечному числу слагаемых в выражениях (1) и (2), получают (7) модели скользящего среднего (СО

Х0-^0 + М?-1)*- +М^*»)

авторегрессии (АР)

ХО = -a>At - 1) - ai^t - 2) -... - ap>\t -р) +e(t)(4)

или обобщенную — авторегрессии скользящего среднего (АРСО

Х0 = - f a^t-k)* lb_ke(t-k).

4 = 1              4 = 1(5)

Практическая важность теоремы Вольда состоит в том, что, если из указанных моделей (3) —(5) выбирается наименее подходящая, то все же можно получить приемлемую аппроксимацию процесса, Увеличив порядок модели.

Поскольку оценивание параметров АР-модели приводит к линейным уравнениям, то метод АР-оценивания имеет некоторые преимущества перед методами, основанными на использовании СС и АРСС моделей, и требующих решения нелинейных уравнений. Исходя из этого, основное внимание было уделено моделированию пульса на основе АР-модели, что не исключает возможности использования СС и АРСС моделей.

Если модель вида (4) найдена, то достаточно просто можно определить и спектральные характеристики сигнала, а именно, спектральную плотность мощности (СПМ) сигнала S по формуле

SV) =

1 ♦ £ а«-^^к 4=1

где /- частота, 0 s f S0.5; о,-дисперсия процесса {ef Г»; / - мнимая единица.

Наиболее распространенный способ нахождения оценок параметров АР-модели состоит в решении уравнений Юла-Уокера [8], связывающих между собой параметры АР-модели и автокорреляционную функцию процесса:

- f a_tR(k-Г),     k>0;

ОД-

i=l

- £ a//?(-0+№², k =0, /=1

где RU) - автокорреляционная функция процесса.

В векторно-матричном виде уравнения (7) записываются следующим образом:

Л(0) Я(-1) ... R(-p)    [1

R(V) R(Q) ... Я(-р + 1) а,

R(p) R(p - X) ”.    R(6) dp

Исходя из свойств четности автокорреляционной функции и теплицевой структуры автокорреляционной матрицы, входящей в уравнение (8), Левинсон и Дурбин [9, 10) предложили эффективный в вычислительном отношении алгоритм решения уравнения (8). Этот алгоритм позволяет последовательно вычислять наборы параметров (an, о?), (azi, ап, (^),.... (а_Рь а_Рг,.... а_рр, ^.Дополнительный индекс введен для обозначения порядка АР-модели. Последний набор коэффициентов порядка р представляет собой искомое решение. Алгоритм Левинсона-Дурбина инициализируется коэффициентами

Л(1) ^а,,= Л(0)’

-a?i)/?(0).

а рекурсии для к = 2, 3,.... р производятся по соотношениям

аи =

(        k-1                * 1

-аД ед + У a_t_,,_tR(k-Г)

аи ” ам-нл + akkak-o-v

о* “(1 -atodi-f.

Однако на практике значения автокорреляционной функции обычно неизвестны, а известны лишь наблюдения процесса (Х0). XI).....Х^ “ 0)-

В этом случае оценку автокорреляционной функции можно получить по выражению

1 N-k-X

.§, ^WL        (М)

где Rtf)- несмещенная оценка автокорреляционной функции,

* = 0,1,2..... М, M^N-X.

Вместо оценки (14) в работе (111 было предложено выражение

- 1 ЛА"^1

MV"n ^*n*k_W.          ₍₁₅₎

где к - 0, 1, .... М, которая, по мнению авторов, имеет меньшую чем (14) среднеквадратическую ошибку для многих конечных наборов данных. При длинных записях данных оба выражения (14) и (15) дают практически идентичные результаты.

Важным этапом АР-оцснивания является выбор порядка модели (4). Поскольку наилучший порядок модели, как правило, заранее неизвестен, то на практике приходится использовать несколько порядков модели. При этом рассчитывают какой-либо критерий ошибки, по которому производится выбор оптимального значения порядка. Наиболее часто применяются критерии финальной ошибки прогнозирования ФОП [121

ФОПМ-о?^±1.            (16)

где N - число отсчетов данных, и информационный критерий Акаике ИКА [131

ИКА(р) = ^1п(о?) + 2р.                    (17)

Выбор порядка модели р осуществляется по минимуму соответствующего критерия. Однако при анализе реальных данных приходится быть весьма осторожным, выбирая порядок модели по критериям (16) и (17), так как функции ФОП(р) и ИКА(р) иногда имеют несколько локальных минимумов, а модель, соответствующая глобальному минимуму, не всегда является наиболее адекватной реальному процессу.

Отметим также, что, с точки зрения теории линейного предсказания (по методу наименьших квадратов) (14J, величину eW из выражения (4) можно рассматривать как ошибку прямого предсказания порядка р, т.е. ошибку предсказания величины yW по наблюдениям у (f-1),..., y(f-p):

ex..., t-p),               (18)

где y^t It - 1,..., t - p) = at \^t - *) - прогноз величины у (О.

4=1

Структурная схема, соответствующая такому трактованию величины, представлена на рис. 4.

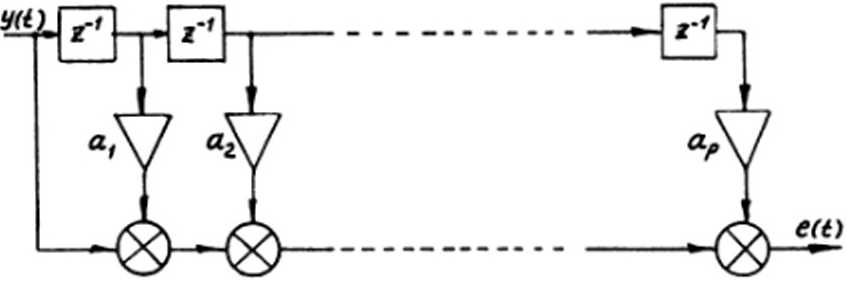
Рис. 4. Структурная схема АР-фильтра, реализованного на линии задержки с отводами

Аналогично выражению (/£) вводится ошибка обратного предсказания г (О, определяемая в виде rVt-l^y^t-p-l'l-^t-p-X /1-р.....Г —1),       (19)

где y(t - р - 1 /1 - р .....f-l)= § b_p-k+\y(t - k) - прогноз величины

*■1

х?-р - О-

При этом для скалярных процессов теоретически а, = Ьь(20)

где i - 1, 2

Если ввести обозначения e^t) и г^ для ошибок прямого и обратного предсказания р-го порядка, то связь между ними определяется в виде [15]

^р+ХО = ^0 -К^-НГрЦ - 1);(21)

гр*М = ^1-1')- ^t ер (Г),(22)

где К\ , К*_р - так называемые коэффициенты отражения вперед и назад.

Использование выражений (18)-(22) позволяет структурно представить АР-модсль в виде решетчатого фильтра, который изображен на рис. 5.

Для детального понимания последующего материала отметим, что теоретически для скалярного процесса

^р-и = ^р+< = - Op+^p+t.                   (23)

а значит, параметры решетчатого фильтра автоматически приходится вычислять в процессе рекурсий алгоритма Левинсона-Дурбина в соответствий с (9)-(13) и (23). Таким образом, решетчатую структуру можно рассматривать как альтернативную для реализации передаточной функции фильтра, изображенного на рис. 4. Хотя решетчатая структура не обладает минимальным числом умножителей и сумматоров для реализации передаточной функции, она имеет ряд преимуществ по сравнению с реализацией на линии задержки с отводами. К числу наиболее значимых преимуществ решетчатой формы реа-

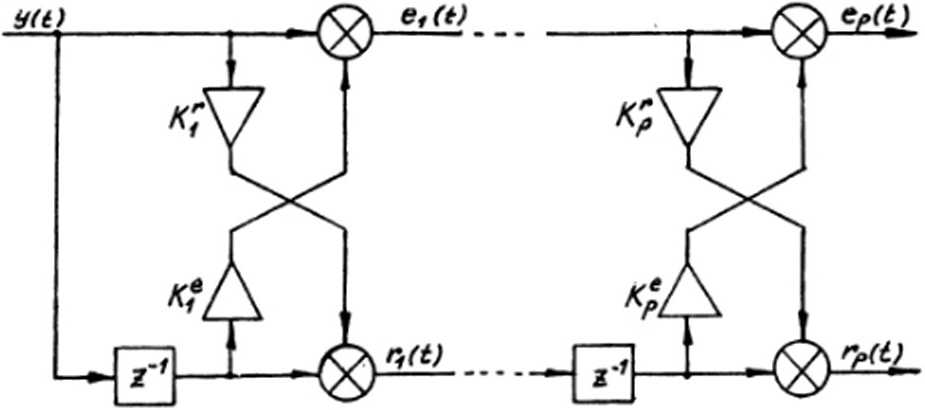
Рис. 5. Решетчатая структура АР-фильтра лизании относится ортогонализация входного сигнала, что приводит к быстрой сходимости алгоритмов оценивания параметров в режиме слежения. Кроме того, ортогональность сигналов, распространяющихся в решетчатом фильтре, и его каскадная структура позволяют увеличивать порядок фильтра, не изменяя параметры предыдущих каскадов.

Другие преимущества использования решетчатых АР-фильтров для моделирования пульсового сигнала будут видны из дальнейшего материала.

Результаты моделирования и возникающие проблемы

Теперь перейдем к описанию и обсуждению результатов АР-моделирова-ния фотоплетизмосигналов. Естественно, что при моделировании непрерывных сигналов на цифровой технике одним из важных вопросов является выбор интервала квантования.Теоретической основой для выбора интервала квантования во времени То =/о"' (см. рис. 3) является теорема Котельникова, определяющая минимально возможную частоту квантования, сохраняющую в квантованном сигнале всю информацию непрерывного сигнала:

/о £ lUx,                             (24)

где/max — максимальная частота в спектре исследуемого сигнала.

При моделировании пульсовых колебаний мы сталкиваемся с задачей сравнения получаемых моделей пульса между собой. При этом наиболее естественным представляется сравнение частоты сердечных сокращений и формы пульсовой кривой. Для сравнения формы кривых и использовались АР-модели. Однако для возможности сравнения получаемых АР-параметров между собой их необходимо оценивать в одном и том же относительном масштабе времени (относительно частоты сердечных сокращений), что позволяет устранить за- висимость модели от физиологического разброса частоты пульса и сравнивать между собой не только модели пульса одного и того же человека, полученные в различные моменты времени, но и пульсы разных людей. Понятно, что частота сердечных сокращений при таком подходе является самостоятельным дополнительным параметром.

Экспериментальные исследования показали отсутствие значимых составляющих фотоплстизмосигнала на частотах, превышающих частоту сердечных сокращений более чем в 9-10 раз. Поэтому, согласно (24), частота дескрити-зации фотоплетизмосигнала во времени должна выбираться не ниже 20 отсчетов на один период пульсовой волны. В эксперименте использовались две типовые частоты дискретизации: 20 и 40 отсчетов сигнала на один период. Типовые объемы выборок при этом составляли 500 и 1000 значений.

Второй важный этап моделирования состоит в выборе порядка АР-модслсй пульса. Следует отметить, что в большинстве случаев оба описанных выше критерия для выбора порядка модели приводили к одним и тем же результатам. При этом оптимальное значение порядка модели пульса при частотах дискретизации 20 отсчетов на период обычно лежало в пределах 13-15 и при частотах 40 отсчетов на период — в пределах 22-26. Пример изменения значений ФОП и ИКА как функций порядка выбираемой модели приведен на графике, изображенном на рис. 6. Для большей наглядности восприятия точки на графике соединены между собой.

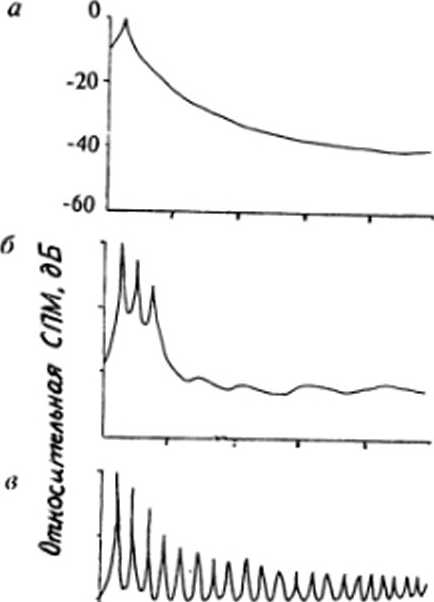
Влияние выбора порядка модели на ее свойства особенно наглядно видны при сравнении спектральных свойств моделей различных порядков. На рис. 7 приведены оценки СПМ пульсосигнала, полученные по выражению (6). Применение моделей заниженного порядка (меньше оптимального) приводит к сглаживанию оценки СПМ, а моделей завышенного порядка (больше оптимального) — к выявлению ложных пиков.

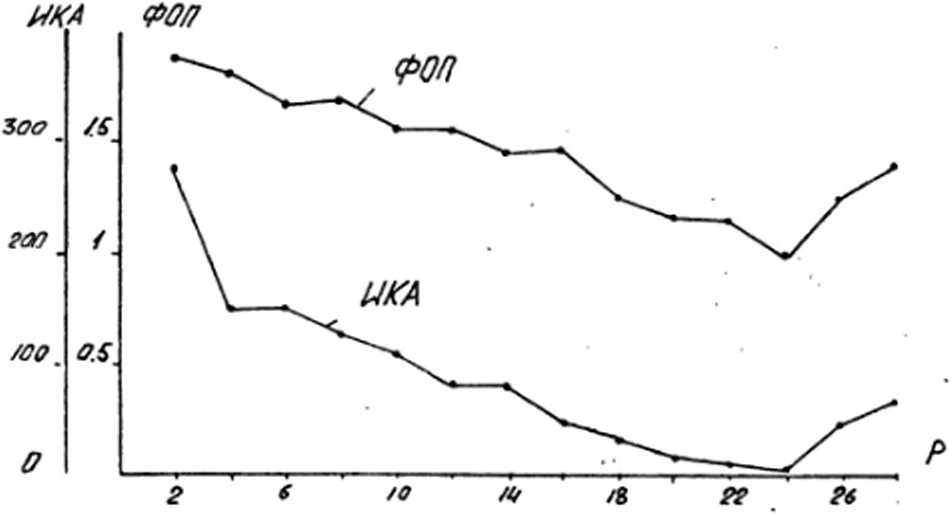
Рис. б. ФОП и ИКА как функции порядка модели

ОЛ ^ 63 0.4 0.5 /

Из сказанного ясно, что при работе с реальными записями пульсовых сигналов в качестве оптимального могут оказаться различные значения порядка модели. Поэтому возникает естественный вопрос: как сравнивать между собой модели различных порядков? Путей для такого сравнения, вероятно, может быть выделено несколько. Однако, по мнению автора, наиболее перспективными являются подходы по сравнению моделей на основе сопоставления СПМ сигналов, полученных при оптимальных значениях порядков моделей, и сравнение коэффициентов отражения АР-моде-ли. Напомним, что решетчатая структура в силу ортогонализации входного сигнала обеспечивает независимость друг от друга коэффициентов отражения отдельных каскадов.

Необходимость сравнения сигнала по спектральному составу приводит к вопросу о возможности применения для этих целей быстрого преобразова

Рис. 7. Влияние выбора порядка модели на ее спектральные характеристики: а — р - 6 (заниженное значение); б — р - 24 (оптимальное значение): в—р-32 (завышенное значение)

ния Фурье (БПФ). Подобный подход, например, использовали авторы работы [161. Используя девять первых гармоник сигнала, им удалось типизировать пульсосигнал для трех возрастных групп здоровых пациентов. Если полученный ими результат удастся обобщить на большее число типов, ограничиваясь лишь девятью параметрами, то, безусловно, этот подход найдет широкое применение в практической медицине.

К сожалению, имеющийся в нашем распоряжении экспериментальный материал показал опасность подхода сравнения спектров пульса только на фиксированных частотах, соответствующих основной (/осн) и более высоким (2/осн, 3/оси, .... 9/оси) гармоникам сигнала. В ряде случаев (примерно 5% от общего числа) наблюдалось расположение пиков СПМ на частотах, не кратных основной частоте. При этом наиболее часто второй по величине пик находился не на частоте 2/осн, а в интервале 2.4-2.6/осн- Погрешностями вычислений этот значительный сдвиг объяснить невозможно, так как была проведена неоднократная проверка полученных спектральных АР-оценок рядом других методов (БПФ, гармоническое разложение Писаренко). Физиологическую причину такого явления еще предстоит установить.

С точки зрения моделирования указанный факт говорит о необходимости принимать во внимание весь спектр мощности пульсосигнала, а не только значения мощности гармоник. Следовательно, для хранения информации о спектре понадобятся значительно большие объемы памяти ЭВМ, что становится существенным ограничением при необходимости массовых обследований населения. Использование АР подхода позволяет существенно снизить требования к объемам памяти, так как храниться должны только параметры модели, а значения СПМ могут быть восстановлены по ним в соответствии с выражением (6) в любой момент времени.

Применение описанной методики в условиях клиники показало возможность построения адекватных АР-моделей пульса пациентов в случае отсутствия аритмии сердечных сокращений.

При наличии аритмии построить АР-модель пульса, удовлетворяющую критерию адекватности (71, не удалось. Данный результат не является удивительным, так как при аритмии теряется свойство стационарности входного сигнала и, соответственно, применение АР-модели с постоянными коэффициентами не может дать статистически достоверного результата. Существует, как минимум, два пути решения возникающей проблемы:

• 1)    использование более сложной модели пульсосигнала и более сложного алгоритма оценивания;

• 2)    использование простой АР-модели с заменой оценок значений параметров оценками областей возможных значений параметров.

Одна из возможных моделей формирования пульсосигнала, позволяющая учесть аритмию, приведена на рис. 8. В этой модели величина Т_ССо представляет собой среднее значение периода сердечных сокращений. Текущее значение периода сердечных сокращений определяется в виде суммы:

T« = T«₀*W^k^ (25)

где eUO - дискретный белый шум; W^ - передаточная функция фильтра, моделирующего процесс аритмии.

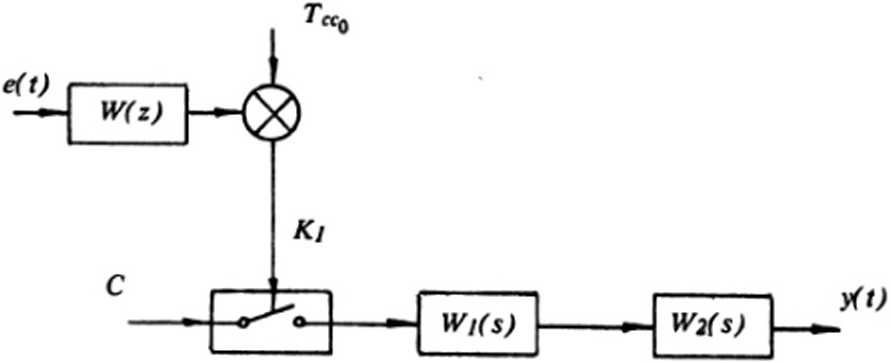
Рис. 8. Модель формирования пульсового сигнала с учетом аритмии

Работа сердца в этой модели описывается в форме импульса, возникающего после прохождения идеального импульса, формируемого ключом Ki, через аналоговый фильтр с передаточной функцией B'jfs). Влияние кровеносных сосудов моделируется передаточной функцией ^(s). В условиях спокойного состояния величину С, поступающую на вход ключа, можно считать постоянной.

Исходя из изложенного, процесс оценки параметров описанной модели разделяется на два этапа: первый — построение модели аритмии; второй — построение обобщенной модели участка сердце — периферические сосуды.

Первый этап задачи с математической точки зрения ничем не отличается от описанной выше задачи параметрической идентификации пульса, и для ее решения с успехом может быть использована процедура АР-оценивания, для которой в качестве входного сигнала используются наблюдения за периодом сердечных сокращений.

Второй этап задачи оказывается принципиально иным, так как связан не с идентификацией процесса, а с идентификацией динамической системы. К настоящему времени разработан достаточно широкий арсенал методов и алгоритмов решения этой задачи при доступных для наблюдения входе и выходе системы (17, 18].

В нашем случае, если используется только фотоплетизмодатчик, входной сигнал, а точнее, время замыкания ключа К\ неизвестно. Конечно, в случае дополнительного параллельного снятия с пациента электрокардиограммы (ЭКГ) или сейсмокардиограммы (СКГ) этот момент времени установить несложно. Более того, при желании можно ввестидатчик давления в аорту, и тогда передаточные функции ^(.s) и W^s) можно оценить по отдельности. Однако использование дополнительных датчиков существенно усложнит аппаратуру и методику проведения процедуры, а эффект от их использования может оказаться незначительным.

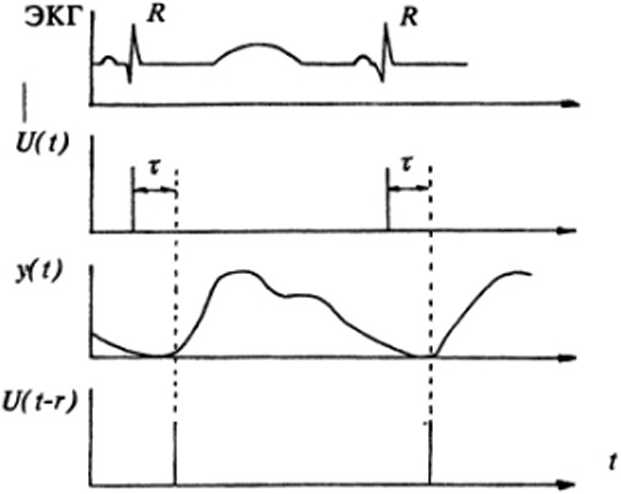
Рис. 9. Формирование псевдовходного сигнала для идентификации модели пульса

В качестве альтернативного подхода в данной ситуации может быть пред ложен метод идентификации на основе вычисления псевдовходного сигнала. Сущность предлагаемого подхода проиллюстрирована на рис. 9. Из наложенного ясно, что в качестве входного для рассматриваемой модели принимается единичный импульс и<Ъ, синхронный с Я-зубцом ЭКГ. При этом

И^фИ^) = е "^(s)^) ,

где г - время транспортного запаздывания; И^И - передаточная функция, характеризующая сосудистую систему без учета транспортного запаздывания.

Понятно, что если интересоваться только формой пульсового сигнала, то, сомножитель е^-ив (26) становится непринципиальным, а значит, реальный входной сигнал и W при идентификации может быть заменен на псевдовходной сигнал u^t - г), который можно вычислить по фотоплетизмограмме, например, по критерию максимальной кривизны [19].

Подход, основанный на использовании вычисляемого псевдовходного сигнала, конечно, не является единственно возможным, однако он позволяет в рамках использования только одного фотоплетизмосигнала решить проблему учета аритмии.

Перспективы практического использования

Вернемся теперь к АР-моделям пульса и кратко рассмотрим возможности их практического применения.

По результатам клинических испытаний, проведенных на базе городской больницы N 26 (С.- Петербург) совместное кафедрой рефлексотерапии ГИДУ Ва представляется возможным использовать параметрические АР-модели для решения двух основных задач пульсодиагностики: персонализации и типизации пульса.

Задача персонализации пульса связана с возможностью определения модели пульса, принадлежащей каждому конкретному человеку. При этом исследования показали, что персональные модели пульсов здоровых пациентов не претерпевают значимых изменений в течение длительного времени (естественно, при одинаковых условиях съема).

Этот результат наводит на мысль о возможности создания экспертных диагностических систем по выделению групп риска. В группу риска будут выделяться пациенты, имеющие значительные отклонения модели пульса от обычной персональной формы. Этот подход прост и дешев и мог бы с успехом использоваться при частых массовых обследованиях работников вредных производств.

Задача типизации пульса более сложна и связана с поиском соответствия определенных АР-моделей пульсосигнала типам пульсов в соответствии с восточной классификацией. Для решения этой задачи требуется значительная база данных для формирования эталонных моделей типов пульса. Создание такой базы является предметом предстоящих исследований, однако уже предварительные экперименты подтвердили эффективность выбора коэффициентов отражения в качестве признаков для кластеризации моделей пульса.

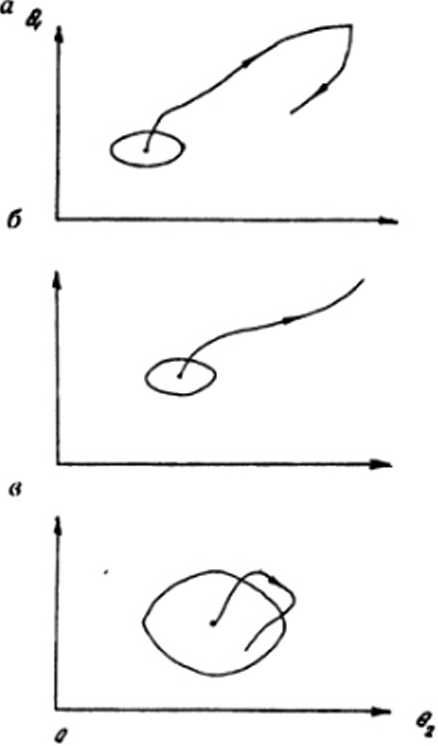
Рис. 10. Варианты изменение параметров модели пульса во времж терапевтических процедур: а — вариант 1; б — вариант 2; в — вариант 3

Другое возможное применение АР-моделей пульса было выявлено в ходе клинических испытаний, проведенных совместно с НИИ онкологии им. акад. Н.Н.Петрова. В ходе этих экспериментов наблюдались изменения параметров модели в ходе проведения внутрисосудистого лазерного облучения крови. Были выявлены три характерных варианта поведения АР-модели периферического пульса. Условно эти варианты изображены на рис. 10. Здесь для удобства зрительного восприятия многомерное пространство пармет-ров (коэффициентов отражения) условно заменено плоскостью, а пространственная траектория изменения параметров во времени — кривой на этой плоскости. Кроме того, на рисунке изображены области, характеризующие физиологический разброс параметров модели в состоянии покоя до начала терапевтической процедуры.

Первый вариант поведения характеризуется малой начальной областью физиологического разброса параметров. При проведении процедуры точка, соответствующая вектору параметров, сначала удаляется от начальной области, а затем появ ляется тенденция возвращения в исходную область. Изменение тенденции от удаления к возвращению обычно наблюдалось на 20-25 мин процедуры.

Второй вариант отличается от первого отсутствием тенденции к возвращению вне зависимости от длительности процедуры. Среди пациентов с такой формой реакции на терапевтическую процедуру имелся летальный исход.

Третий вариант поведения характеризуется большой начальной областью физиологического разброса параметров. В ходе проведения процедуры траектория движения либо вообще не выходит за пределы начальной зоны, либо удаляется от нее на незначительное расстояние.

Обнаруженный феномен, безусловно, еще требует дополнительного экспериментального исследования и теоретического обоснования. Однако уже сейчас может быть сформулирована гипотеза о том, что изменения параметров модели периферического объемного пульса несут в себе информацию о состоянии системы саморегуляции человека. Величина области разброса параметров модели в состоянии покоя, вероятно, характеризует устойчивость системы саморегуляции при внешних воздействиях малой интенсивности, что является возможным аналогом (естественно, только с концептуальной точки зрения) технического понятия "устойчивость в малом". Наличие тенденции к возвра- щению параметров в исходную область в ходе проведения терапевтической процедуры, очевидно, свидетельствует о включении дополнительных регулирующих систем организма в ответ на внешнее воздействие большой интенсивности, что является возможным аналогом технического понятия "устойчивость в большом".

Если предлагаемая гипотеза получит экспериментальное подтверждение и теоретическое обоснование, то откроется путь к созданию диагностических систем, позволяющих индивидуализировать интенсивность и длительность широкого круга терапевтических процедур и дающих ответ на вопрос о целесообразности проведения процедуры конкретному пациенту в конкретный день.

Автор отдает себе отчет в том, что на сегодняшний день попытки практического применения АР-моделей пульса поставили больше вопросов нежели дали ответов. Однако перспективность исследования в этом направлении несомненна, и для успеха требуется накопить значительный экспериментальный материал.

В заключение автор хотел бы поблагодарить профессора Л. Льюнга (Университет г. Линкопинг, Швеция) за плодотворные обсуждения проблем моделирования пульсосигналов, заведующего кафедрой рефлексотерапии ГИДУВа д-ра мед. наук А.Т.Качана и канд.мед.наук П. X. Варнакова за организацию клинических испытаний на базе больницы N 26 С.-Петербурга, зам. главного онколога С.-Петербурга канд. мед. наук М.Л.Гельфонда за организацию работ совместно с НИЙ онкологии им. акад. Н. Н. Петрова, а также коллектив лаборатории Института аналитического приборостроения РАН С.-Петербурга, возглавлявшей ся до недавнего времени д-ром техн, наук А.М.Корнеевым , за помощь в создании программного и аппаратного обеспечения экспериментальных работ и участие в их проведении.