Параметрические радиотехнические системы

Одним из основных направлений расширения информационных возможностей радиотехнических методов извлечения и передачи информации является исследование механизмов взаимодействия электромагнитных волн с процессами и полями другой физической природы – механическими, сейсмическими, электрохимическими, плазменными, в результате которых возможно создание новых технологий дистанционного исследования объектов и сред с более высокими качественными параметрами. Традиционно радиолокационный метод дистанционного извлечения информации используется для оценки интегральных параметров объектов – координат, скорости движения, эффективной поверхности рассеивания [1], однако по мере совершенствования тактико-технических параметров объектов радиолокации – скрытности, маскировки, скорости движения, маневренности – требуется адекватное развитие средств обнаружения.

Имеются проблемы передачи и приема информации через границы сред с разным типом проводимости, в частности при обеспечении связи с подводными морскими аппаратами.

Классическая связь с использованием электромагнитных волн не позволяет получить прием и передачу сигналов с глубин более десятка метров из-за высокого поглощения энергии радиоволн морской водой [2, 3].

Традиционно для связи в воздушной среде используются радиоволны, а в морской – ультразвуковые колебания, однако эти методы имеют существенные ограничения по дальности и глубине приема. Принципиально новые результаты можно получить при использовании эф

фектов параметрического взаимодействия обоих видов колебаний на границе раздела вода-воздух [4].

В настоящей статье рассматривается ряд прикладных задач радиофизики, общим принципом которых является использование эффекта модуляции неэнергетических параметров радиоволн, существенно улучающих чувствительность и информационную эффективность систем дистанционного зондирования.

Постановка задачи

Типичными примерами подобных задач могут быть: граница раздела вода-воздух; ионопроводящая среда (земля)-металл; металл-диэлектрик; плазма-воздух; металл-воздух; биохимические среды с существенно различающимися свойствами и т.п.

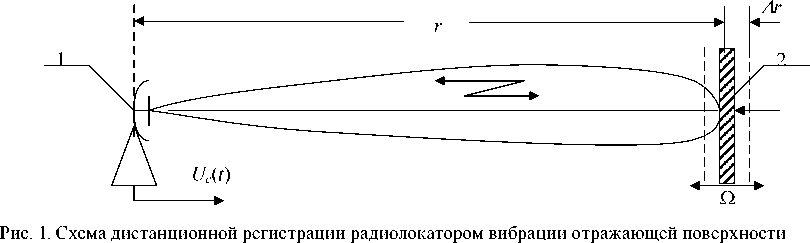
На рис. 1 приведена простейшая схема параметрической модуляции отраженной электромагнитной волны радиолокатора (РЛС) колеблющейся границей раздела металл-воздух.

В этой схеме передатчик РЛС облучает некоторую металлическую поверхность, периодически колеблющуюся с амплитудой A r и частотой Q = 2 п F и находящуюся от РЛС на расстоянии r , и принимает отраженный сигнал, модулированный по частоте и фазе в виде

U c ( t ) = Um ™

tot+7Tsini"‘+ф)+Aфsin"‘) ■

где to = 2n f - несущая частота; Ato - девиация частоты за счет допплеровского смещения;

Ar                             с2

Аф = 2 п— - амплитуда сдвига фаз; X — — - длина волны; Ato = to— ; с - скорость света;

X                         fс и - скорость колебаний металлической поверхности.

За период T — —, при скорости колебаний: и — —, допплеровское приращение частоты составит:         FT

Ato = to —.(2)

cT

Чувствительность РЛС к смещению отражающей границы будет равна по частоте

Arn — = A r	2 rn _ 2 rn F			Рад	.                                                            (3)
	cT		c	м • с
Чувствительность по фазе:
Аф _	to	Рад			(4)
A r	c	м • с	.
Из сравнения (3) и (4) получим:

^Ato _ ^Aф

A r  A r

Из (5) формально кажется, что чувствительность по частоте выше чувствительности по фазе на частоту колебаний 2 F . Однако из-за разной размерности частотного и фазового сдвига прямое сопоставление двух методов неправомерно, поскольку детектирование частотного и фазового сдвигов производится разными схемными решениями.

Рассмотрим частный случай:

f = 109 Гц; Ar = 10-3 м; F = 103 Гц. Из (4) и (5) получим Аф = 1,2град или относительное град м

. Аф . _ приращение фазы: — = 1,2 A r

Частотный сдвиг, согласно (3):

Δω Δ r

2 ⋅ 2 π⋅ 10 ⁹  33 Гц

--------5 10 = 66 * 10 --- .

3 ⋅ 10 ⁸                    м

В данном случае частотный метод, безусловно, чувствительнее фазового и реализуется более простым детектором.

В другом частном случае, например при необходимости измерения расстояний до малоподвижной отражающей поверхности с малой частотой вибрации, когда и^ 0 и Аю^ 0, фазовый метод позволяет решить подобную задачу, а частотный – нет.

Перечислим ряд практических задач из области радиолокации, которые могут быть решены параметрическим методом с существенно более высокой информационной эффективно- стью, по сравнению с традиционными методами:

• -    задачи дистанционного распознавания воздушных, малозаметных целей путем выделения частоты вибраций двигателей, корпуса носителя, плазменного следа двигателей и т.п.;

• -    дистанционная дефектоскопия мест повреждения магистральных нефте- и газопроводов с аэрокосмических носителей [5];

• -    обнаружение и отслеживание движущейся транспортной техники под покровом леса;

• -    определение собственных координат маневренных средств противовоздушной обороны с помощью системы пассивных наземных переотражателей, модулированных специальным кодом вибраций;

• -    радиолокационная дефектоскопия железнодорожных путей [6].

Интересные возможности открывает параметрический метод в задаче радиосвязи с подводными морскими аппаратами, а также в реализации новых методов геофизических поисков на основе сейсмоэлектрических эффектов взаимодействия электрических и сейсмических полей на двойном электрическом слое: электронный проводник или диэлектрик – ионопроводящая среда (земля) [7, 8].

Далее рассмотрим возможности использования параметрического метода путем искусственного воздействия исследуемых объектов полями другой физической природы - механи-

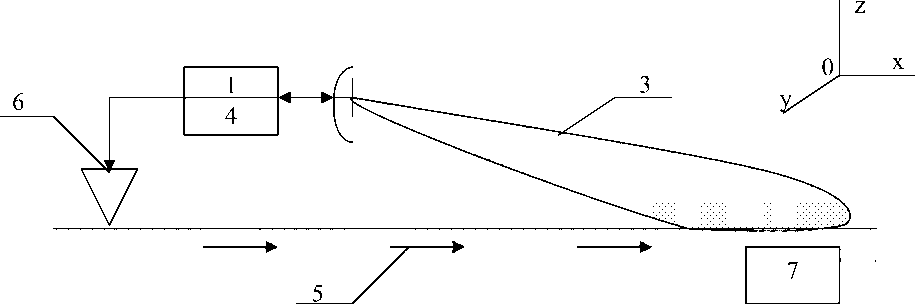
Рис. 2. К реализации способа дистанционного обнаружения подповерхности объекта параметрическим методом ческими, акустическими либо электромагнитными, существенно отличающимися по частоте от рабочей частоты зондирующего сигнала РЛС.

Чрезвычайно актуальной задачей является дистанционное обнаружение и уничтожение мин и минных полей. Сегодня во многих горячих точках – Ангола, Афганистан, Ирак, Чечня, Дагестан – минная опасность подстерегает человека на каждом шагу. Недаром ООН объявила эту проблему как общемировую.

Нами запатентован новый способ обнаружения мин на основе параметрического взаимодействия электромагнитных и акустических волн на поверхности земли в районе зоны поиска [7].

Существо способа заключается в возбуждении в объектах поиска собственных механических колебаний с помощью сейсмического излучателя поверхностных акустических волн Релея.

На рис. 2 изображена схема реализации способа, по которой передатчик радиолокатора 1 сканирует поверхность земли 2 качающимся лучом 3 впереди транспорта – носителя поисковой установки, а приемник 4 принимает отраженные сигналы, демодулирует и передает в процессор обработки информации.

Поверхностная волна Релея 5 распространяется от сейсмического излучателя 6 и возбуждает механические колебания во всех приповерхностных неоднородностях, включая объект поиска 7. Последние существенно отличаются по частоте и амплитуде вибраций от других объектов, что и является информационным признаком распознавания мин. Разница в скоростях распространения электромагнитных и акустических волн используется для временной развязки отраженного радиолокационного сигнала от первичного поля передатчика.

Если интенсивность сейсмоакустической волны у поверхности объекта поиска будет равна I_а , а площадь его поперечного сечения равна S , то амплитуда силы звукового давления на поверхность объекта поиска составляет: P = I a х S .

Поскольку уравнение динамики поверхности объекта без учета влияния среды можно записать как mdtx — P = °’ (6)

то ускорение смещения поверхности объекта d2 x

dt ²

P m

где m – масса объекта поиска.

Механический резонанс корпуса объекта поиска увеличивает действие силы Р в число раз, равное величине добротности Q, поэтому выражение (7) можно записать как

P × Q a =------ .

m

Вследствие того, что интенсивность релеевской волны у поверхности границы раздела затухает обратно пропорционально расстоянию r, оценить величину действующей силы у поверхности объекта можно с помощью приближенного соотношения:

P = I 1 Ru- S , r

P где 11 = —12 - интенсивность сейсмоакустической волны вблизи источника; Ru - эффектив-П Ru

ныи радиус контактной поверхности излучателя сейсмоакустических волн (сигналов) с грунтом; Р 1 - мощность излучателя сейсмоакустических волн (сигналов); О - площадь поверхности корпуса объекта поиска, перпендикулярная действующей силе; r – расстояние до объекта поиска.

Из решения уравнения (1) смещение корпуса объекта под действием силы акустического давления

х - PQdt,. 00 ^m

где τ – время действия силы акустического давления.

При единичном ударе на интервале 0-т величина P = const, из выражений (8) и (9) полу чаем:

_х-Pi_ R^sQ е x             О т .

nR,, r m

При периодическом повторении сейсмоакустических импульсов отраженный от объекта радиолокационный сигнал можно записать как

n

U ( t ) = Um E sin i=1

, . 2пх .

to i t +-- sin Q t I

^ i        J

где to i t = 2 n f - циклическая частота радиолокационного сигнала; X i - длина волны радиолокационного СВЧ сигнала; О = 2 п F - циклическая частота сейсмоакустического сигнала; i – текущий номер гармоники.

Для периодического импульсного сигнала, когда 90 % его энергии сосредоточено в первой гармонике, фазовый сдвиг первой гармоники принимаемого радиолокационного эхо-сигнала будет равен:

∆ϕ

= 2 п х • _О = x i ^sin

Путем фазового детектирования отраженного от объекта радиолокационного сигнала, выделяя коэффициент фазовой модуляции Аф , можно получать информацию о смещении х , прямо

Q пропорциональном, согласно выражению (10), отношению x = А —.

Для одинаковых по размеру объектов величина этого смещения тем больше, чем выше добротность его корпуса и меньше масса. Для объектов искусственного происхождения, типа мин, параметр ~ будет явно отличаться от естественных объектов (например камней) или ис-m кусственных (металлический мусор).

Следующей проблемой, решаемой параметрическим методом, является обнаружение мелких металлических предметов, например драгоценных металлов, а также опасных металлических изделий – оружия и боеприпасов – через охраняемые проходы.

Традиционно эта проблема решается использованием низкочастотных электромагнитных полей на основе возбуждения в объектах обнаружения вихревых токов и регистрации вторичного магнитного поля этих токов.

Однако используемые системы не обладают достаточно надежными характеристиками распознавания, особенно по работе по вышеуказанным объектам поиска.

Нами запатентован способ и устройство реализации указанной задачи на основе совместного использования двух электромагнитных полей, существенно разнесенных по частоте [9].

Низкочастотное поле накладывается на контролируемый проход для возбуждения собственных механических колебаний объектов поиска за счет сил Лоренца, возникающих при взаимодействии возбуждающего электромагнитного поля и наведенных в объекте поиска вихревых токов. При облучении прохода полем сверхвысокочастотного диапазона из отраженного поля выделяются сигналы частоты наведенных вибраций объектов поиска. Подобная система должна использовать нейрокомпьютерную программу обучения, позволяющую существенно улучшить качество обнаружения и распознавания.

Принципиально новые возможности в области радиосвязи с подводными морскими аппаратами может открыть параметрический метод на основе эффектов взаимодействия электромагнитных и ультразвуковых волн на границе раздела вода-воздух [4]. Традиционно для этой цели в канале воздух-вода используется передача радиосигналов с береговой радиостанции на низких и сверхнизких частотах с приемом на буксируемую антенну. В связи с высоким поглощением электромагнитных волн морской водой глубина подводного приема ограничивается диапазоном 10-100 м. Для ее увеличения используются сверхнизкие рабочие частоты, в частности в американских проектах SANGUIN и SEAFARER применяются частоты соответственно 75 Гц и 45 Гц со сверхмощным антенным полем передатчика до 10 мВт при размере антенного полотна 100 x 100 км [2].

Нашими работами в Красноярском политехническом институте впервые теоретически и экспериментально обоснована возможность создания параметрических каналов передачи информации воздух-вода и вода-воздух с существенным снижением зависимости выбора рабочей частоты от поглощения радиоволн морской водой [10, 11].

I

I

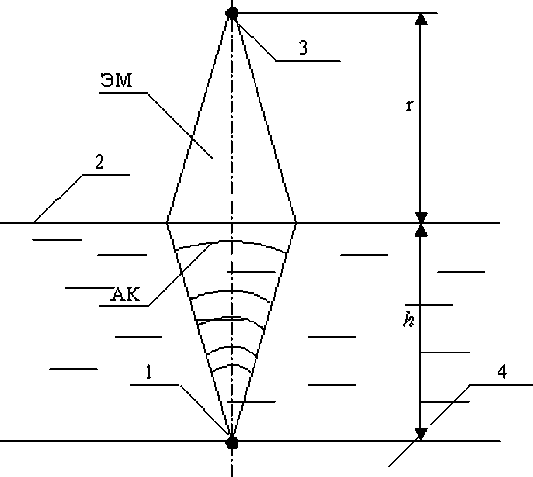
Рис. 3. Взаимное расположение приемопередатчиков относительно границы раздела: 1 – точка расположения акустического излучателя; 2 – граница раздела вода-воздух; 3 – точка расположения приемопередатчика электромагнитного канала; 4 – корпус носителя; АК – акустический канал; ЭМ – электромагнитный канал

Физической основой параметрического подводного радиоприема является эффект демодуляции электромагнитной волны ультразвуком, «подсвечивающим» водную поверхность излучателем, расположенным на подводном аппарате (рис. 3).

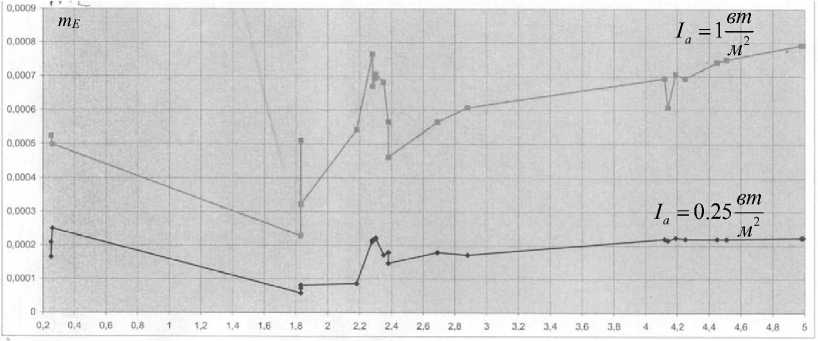
На рис. 4 представлены экспериментально полученные зависимости коэффициента параметрической демодуляции от электропроводности воды при двух значениях плотности потока мощности ультразвука - 0,25 1 вт/м². Эксперимент производили в лабораторном бассейне размером 0,5 х 0,5 х 1,5 м.

В качестве ультразвукового излучателя использовали набор дисков из титанита бария с рабочей частотой f = ¹⁵ кГц. ^a

Электромагнитное поле частотой f э = 16,5 кГц создавалось горизонтальным диполем с заводняющими пластинами, выполненными из титана. Акустический и электромагнитный излучатели располагались по противоположным сторонам бассейна на дистанции 1200 мм.

Прием велся на электрический заводненный диполь длиной 100 мм.

При одновременном излучении обоих видов полей на приемном диполе с помощью спектрального анализатора измеряли коэффициент параметрической демодуляции m E как отношение принимаемого сигнала разностной частоты F = f_э - f a = 1.5 кГц к сигналу частоты возбуждающего ЭМ поля f , = 16,5 кГц.

Как видно из графиков, коэффициент m_E существенно возрастает с ростом электропроводности воды от 1,8 до 5 сим/м и интенсивности акустического излучения I _а. В районе низкого

^ Ef. - f.

Рис. 4. Экспериментальные зависимости коэффициента демодуляции m_E = — э²-^ от электропроводности воды σ , см/м                                                             ^Ef э

уровня электропроводности σ = 0.2 сим/м и 2,2-2,4 сим/м наблюдались аномальные изменения коэффициента mE, что можно объяснить изменением соотношений токов смещения и прово-

E димости в воде. При низком уровне проводимости преобладают токи смещения, и повышен ное значение коэффициента mE объясняется модуляцией диэлектрической проницаемости воды ультразвуком.

При проводимости ст = 2.2 - 2.4 сим/м, по-видимому, действуют оба механизма как моду ляции б, так и ст.

Для расчета энергетического выигрыша параметрического канала по сравнению с клас- сическим используем соотношение напряженностей электромагнитного поля в зоне приема на поверхности воды для случая плоского фронта волны исходя из формулы Остина для вертикальной электрической компоненты [2]:

1 2 πµ 0        Q ^0.5

E _{1 z} = f_эIL

2 сH i σ 3

cos θ -δ r e -δ _a r

r asin c a

мкв

м

где ц₀ - магнитная проницаемость вакуума, Гн/м; с - скорость света м/с; H i - высота ионосферы, м; ст - эффективная проводимость воды, см/м; f - частота колебаний, Гц; I - ток в антенне, А; L – эффективная длина антенны, м; δ а – коэффициент атмосферного затухания, дБ/км; r – расстояние между передатчиком и приемником, м; а – радиус Земли, м; θ – угол поворота диаграммы направленности антенны передатчика относительно приемной антенны,

δ a

0.0014 ( f П ^0,6 - f K ^0,6 )

_c 0.6

С учетом приближенного граничного условия Леонтовича горизонтальная компонента электрического поля на поверхности воды для классического способа приема

E xK =          E z .                                           (13)

Для параметрического:

E xП = m E ^{2 π fП ε 0} E 1 z . σ

Величина коэффициента параметрической демодуляции m_E выбирается в соответствии с описанными выше экспериментальными данными: m E = 10 - 3 JI , где I a - интенсивность ультразвука на поверхности воды.

Отношение горизонтальных компонент напряженностей параметрического и классиче- ского методов:

ExП

ExK

f П I П L n ^п „

₁ П _m f_KI_KL_K П ^/2 KKK_K

f ^П |    -' а^{аП 5 аК} ) ^r

I

I ^fK )

Поскольку коэффициент полезного действия п передающего антенного поля растет про-

П12   г„ порционально квадрату рабочей частоты, то можно принять отношение —Пг = —. С учетом

Ч /2 fK

K допущения f П □ fK в формуле (15) опустим коэффициент поглощения волны атмосферой для классического метода 5aK □ 5an и, принимая условие —П = 1 из (15), получим расчетное соот-ExK ношение для коэффициента выигрыша параметрического метода над классическим по электрическому моменту передающих антенн:

IL

_ П П

в

IKLK

f              -<

^П me

E

V fK )

⁵ аП ^г

.

В [4] частотная зависимость коэффициента К в принималась как ста КПД передающей антенны п с увеличением частоты.

( f 32

V -л- j , т.е. без учета ^ро-

В таблице приведены расчетные данные, полученные с использованием этой формулы для расстояния от передающего центра r = ⁵⁰⁰⁰ км.

Как видно из этой таблицы, на частоте 75 Гц, соответствующей системе SANGUIN, наибольший выигрыш параметрического метода по электрическому моменту передающей антенны составляет величину K в = 313. С учетом того, что длина антенны системы SANGUIN составляет величину L_K = 100 км, а мощность передатчика 10 МВт, то подобный выигрыш параметриче-

Таблица. Зависимость коэффициента выигрыша K в от частоты излучения параметрического f П и классического F K метода передачи сигналов

FК, Гц fП, Гц 104 2∙104 5∙104 105 1 28∙103 65∙103 2∙105 2∙105 10 285 671 1980 1800 75 56 187 313 115 100 2,8 65 , 19,6 19 ского метода означает, что последний обеспечит ту же дальность при длине антенны в 10 км с мощностью передатчика 10 кВт.

На частоте модуляции F = f_K = 1 Гц прием сигналов возможен на глубине 1000 м, что недостижимо с использованием никакого другого метода передачи.

Реализация обратного канала передачи информации из-под воды в воздух возможна путем использования эффекта параметрической модуляции электромагнитных волн ультразвуком на границе раздела вода-воздух на основе трех физических пограничных эффектов:

• -    модуляции поверхности воды ее колебательным смещением под действием акустического давления, излучаемого подводным передатчиком с модуляцией несущей частоты ультразвука передаваемым сообщением;

• -    модуляции диэлектрической проницаемости воды;

• -    модуляции электропроводности воды.

Поскольку первый эффект по уровню (индексу) модуляции на порядок превосходит два других, то в работе [4] приводятся результаты оценок тактико-технических параметров обрат -ного канала передачи на основе считывания с поверхности воды информационного сигнала с помощью активного СВЧ-радиолокатора, располагаемого на аэрокосмических носителях.

По этим оценкам возможна реализация канала передачи с ПА на космический аппарат с глубины погружения ПА до 2000 м и высоте полета КА около 400 км при приемлемой для обоих носителей мощности электропотребления 10 кВт на ПА и 100 Вт на КА.

Заключение

Рассмотрены методы реализации особого класса радиосистем - параметрических, основанных на взаимодействии электромагнитных и других видов физических полей (механических, акустических, электрохимических и т.п.), на границах раздела сред с разным типом проводимости, позволяющих по-новому решить ряд прикладных задач дистанционного извлечения и передачи информации.

Приведены результаты теоретических оценок достижимых параметров для задач обнаружения малых подповерхностных объектов в земле, в охраняемых проходах, для решения проблем связи с подводными морскими объектами.

Все описанные в статье основные технические решения защищены патентами Российской Федерации.

Работа выполнена при финансовой поддержке аналитической ведомственной целевой программы «Развитие научного потенциала высшей школы» (2009-2010 гг.) по проекту №2.1.2/775. Работа публикуется при поддержке Программы развития Сибирского федерального университета.